Basic Illumination HANSABA COLLEGE OF ENGINEERING AND TECHNOLOGY

Basic Illumination HANSABA COLLEGE OF ENGINEERING AND TECHNOLOGY, SIDHPUR (098) INSTITUTE GUIDE PANKAJ A PRAJAPATI ELE DEPT. HCET SIDHPUR BRANCH : - ELECTRICAL (C 11) Gohil Amit M. (130980109001) Joshi Jay P. (130980109020) Barot Mahesh P. (130980109002) Pandya Bhrugu I. (130980109003)

Light Source Independent Models Depth Shading • Color or intensity determined solely by "depth" of polygon. • Darker colors or intensities at lower elevations. • Effective in modeling terrain or surface data • Avoids complex calculations of lighting dependent models • Simulates realism

Depth Cueing • Reduce intensity of pixel as the distance from the observer increases • Simulates reduction in clarity as distances from the observer increases • Image fades in the distance • Often used in medical imaging

Light Source Dependent Models What an object looks like depends on • Properties of the light source such as color, distance from object, direction from object, intensity of source • Surface characteristics of object such as color and reflectance properties

Diffuse Reflection using Lambert's Law • Lambert's Law - The intensity of light reflected from a surface is proportional to the cosine of the angle between the vector L to the light source and the normal vector N perpendicular to the surface. • The amount of reflected light is dependent on the position of the light source and the object but independent of the observer's position.

Simple Illumination Model Let I = Illumination intensity Ip = Point light source intensity (white light) kd = Surface reflection coefficient (0<=kd<=1) ß = must be between 0 and 90 degrees A simple illumination model: I = Ipkd(cosß) Since cosß = (L • N)/(||L|| ||N||), then if L and N have unit length then we can use I = Ipkd (L • N)

Ambient Illumination • Ambient light is the illumination of an object caused by reflected light from other surfaces. To calculate this exactly would be very complicated. A simple model assumes ambient light is uniform in the environment. Let Ia = Ambient light intensity ka = Ambient light reflected Then we modify our previous illumination model to I = Iaka + Ipkd (L • N)

Light-source Attenuation • Thus far we have ignored the inverse square law: energy decays with the inverse square of the distance d. L to the light source. Including this term we get I = Iaka + Ipkd (L • N)/d. L 2 • However, due to our previous assumptions of a point light source and uniform ambient light, using the d. L 2 term gives too rapid of a decrease in illumination intensity to look realistic. The 1/d. L 2 term is usually replaced by fatt where fatt = MIN (1/(c 1 + c 2 d. L + c 3 d. L 2), 1) I = Iaka + Ipkd (N • L)*fatt
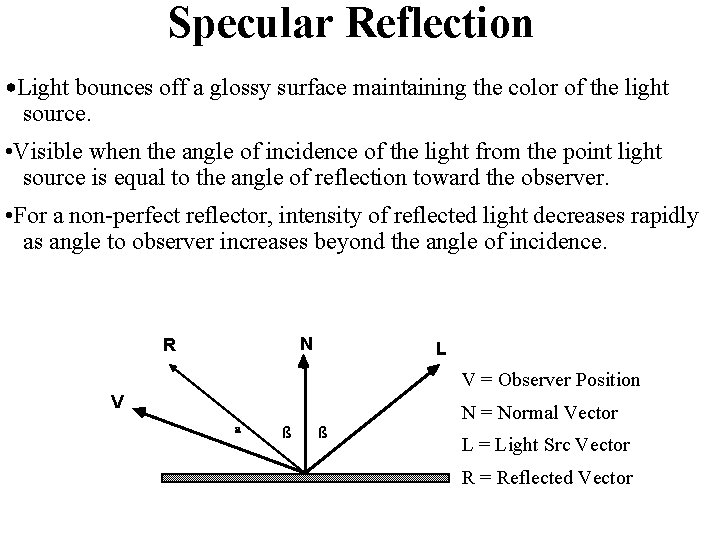
Specular Reflection • Light bounces off a glossy surface maintaining the color of the light source. • Visible when the angle of incidence of the light from the point light source is equal to the angle of reflection toward the observer. • For a non-perfect reflector, intensity of reflected light decreases rapidly as angle to observer increases beyond the angle of incidence. N R L V = Observer Position V a ß ß N = Normal Vector L = Light Src Vector R = Reflected Vector

Phong's Highlighting Term Ipfatt W(ß) cosna Ip = Point light source intensity fatt = Light-source Attenuation W(ø) = Fraction of specullarly reflected light (usually a constant, 0 < = ks) <= 1 n = Specular reflection exponent (perfect reflector n = ∞) cos a = R • V = (2 N(N • L) – L) • V I = Iaka + Ipkd (N • L)*fatt + Specular Component = Ipfatt ks(((2 N(N • L) – L) • V)n This term represents the amount of the light source’s color that should be added!

Implementation Details • Given an RGB Color Space – (A) Ambient Light = Ia – (D) Diffuse Reflection = Ip (L • N)/(||L|| ||N||) fatt – (S) Specular Reflection = Ip* fatt (R • V)n • Given a White Light Source L = (255, 255) • Given a RGB point O = (R, G, B) Ir = Or(A*ka + D*kd) + Lr(S*ks) Ig = Og(A*ka + D*kd) + Lg(S*ks) Ib = Ob(A*ka + D*kd) + Lb(S*ks)

THANK YOU
- Slides: 12