Basic Factory Dynamics Physics should be explained as

Basic Factory Dynamics Physics should be explained as simply as possible, but no simpler. – Albert Einstein © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 1

HAL Case Large Panel Line: produces unpopulated printed circuit boards Line runs 24 hr/day (but 19. 5 hrs of productive time) Recent Performance: • throughput = 1, 400 panels per day (71. 8 panels/hr) • WIP = 47, 600 panels • CT = 34 days (663 hr at 19. 5 hr/day) • customer service = 75% on-time delivery Is HAL lean? What data do we need to decide? © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 2

HAL - Large Panel Line Processes Lamination (Cores): press copper and prepreg into core blanks Machining: trim cores to size Internal Circuitize: etch circuitry into copper of cores Optical Test and Repair (Internal): scan panels optically for defects Lamination (Composites): press cores into multiple layer boards External Circuitize: etch circuitry into copper on outside of composites Optical Test and Repair (External): scan composites optically for defects Drilling: holes to provide connections between layers Copper Plate: deposits copper in holes to establish connections Procoat: apply plastic coating to protect boards Sizing: cut panels into boards End of Line Test: final electrical test © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 3

HAL Case - Science? External Benchmarking • but other plants may not be comparable Internal Benchmarking • capacity data: what is utilization? • but this ignores WIP effects Need relationships between WIP, TH, CT, service! © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 4

Definitions Workstations: a collection of one or more identical machines. Parts: a component, sub-assembly, or an assembly that moves through the workstations. End Items: parts sold directly to customers; relationship to constituent parts defined in bill of material. Consumables: bits, chemicals, gasses, etc. , used in process but do not become part of the product that is sold. Routing: sequence of workstations needed to make a part. Order: request from customer. Job: transfer quantity on the line. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 5

Definitions (cont. ) Throughput (TH): for a line, throughput is the average quantity of good (non-defective) parts produced per unit time. Work in Process (WIP): inventory between the start and endpoints of a product routing. Raw Material Inventory (RMI): material stocked at beginning of routing. Crib and Finished Goods Inventory (FGI): crib inventory is material held in a stockpoint at the end of a routing; FGI is material held in inventory prior to shipping to the customer. Cycle Time (CT): time between release of the job at the beginning of the routing until it reaches an inventory point at the end of the routing. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 6

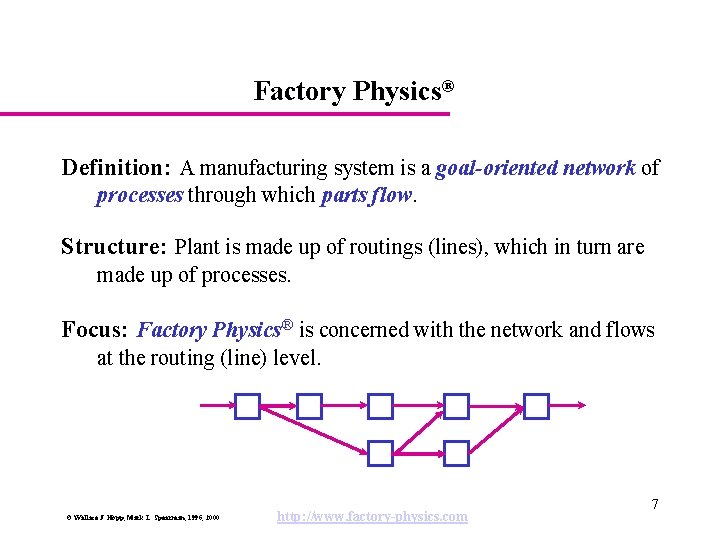
Factory Physics® Definition: A manufacturing system is a goal-oriented network of processes through which parts flow. Structure: Plant is made up of routings (lines), which in turn are made up of processes. Focus: Factory Physics® is concerned with the network and flows at the routing (line) level. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 7

Parameters Descriptors of a Line: 1) Bottleneck Rate (rb): Rate (parts/unit time or jobs/unit time) of the process center having the highest long-term utilization. 2) Raw Process Time (T 0): Sum of the long-term average process times of each station in the line. 3) Congestion Coefficient ( ): A unitless measure of congestion. • Zero variability case, = 0. • “Practical worst case, ” = 1. • “Worst possible case, ” = W 0. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 Note: we won’t use quantitatively, but point it out to recognize that lines with same rb and T 0 can behave very differently. http: //www. factory-physics. com 8

Parameters (cont. ) Relationship: Critical WIP (W 0): WIP level in which a line having no congestion would achieve maximum throughput (i. e. , rb) with minimum cycle time (i. e. , T 0). W 0 = r b T 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 9

The Penny Fab Characteristics: • Four identical tools in series. • Each takes 2 hours per piece (penny). • No variability. • CONWIP job releases. Parameters: rb = 0. 5 pennies/hour T 0 = 8 hours W 0 = 0. 5 8 = 4 pennies = 0 (no variability, best case conditions) © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 10

The Penny Fab © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 11

The Penny Fab (WIP=1) Time = 0 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 12

The Penny Fab (WIP=1) Time = 2 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 13

The Penny Fab (WIP=1) Time = 4 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 14

The Penny Fab (WIP=1) Time = 6 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 15

The Penny Fab (WIP=1) Time = 8 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 16

The Penny Fab (WIP=1) Time = 10 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 17

The Penny Fab (WIP=1) Time = 12 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 18

The Penny Fab (WIP=1) Time = 14 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 19

The Penny Fab (WIP=1) Time = 16 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 20

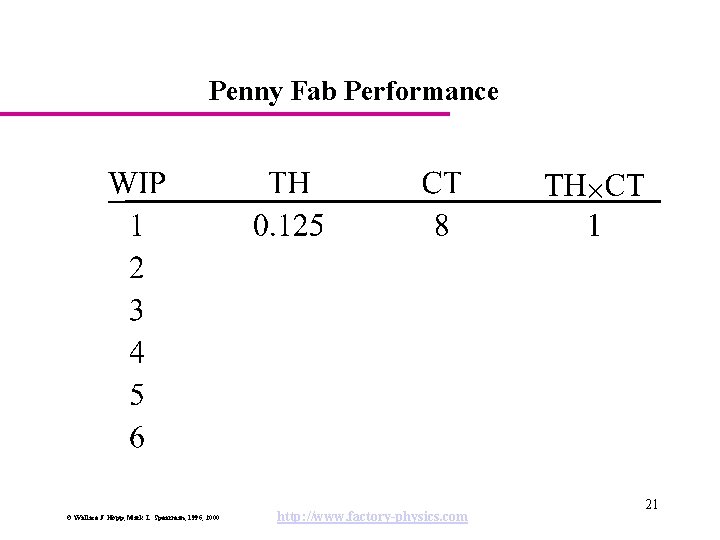
Penny Fab Performance © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 21

The Penny Fab (WIP=2) Time = 0 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 22

The Penny Fab (WIP=2) Time = 2 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 23

The Penny Fab (WIP=2) Time = 4 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 24

The Penny Fab (WIP=2) Time = 6 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 25

The Penny Fab (WIP=2) Time = 8 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 26

The Penny Fab (WIP=2) Time = 10 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 27

The Penny Fab (WIP=2) Time = 12 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 28

The Penny Fab (WIP=2) Time = 14 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 29

The Penny Fab (WIP=2) Time = 16 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 30

The Penny Fab (WIP=2) Time = 18 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 31

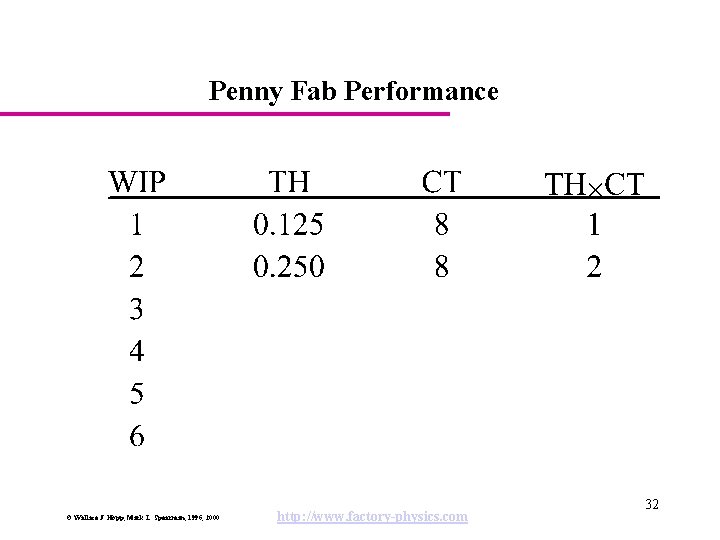
Penny Fab Performance © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 32

The Penny Fab (WIP=4) Time = 0 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 33

The Penny Fab (WIP=4) Time = 2 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 34

The Penny Fab (WIP=4) Time = 4 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 35

The Penny Fab (WIP=4) Time = 6 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 36

The Penny Fab (WIP=4) Time = 8 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 37

The Penny Fab (WIP=4) Time = 10 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 38

The Penny Fab (WIP=4) Time = 12 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 39

The Penny Fab (WIP=4) Time = 14 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 40

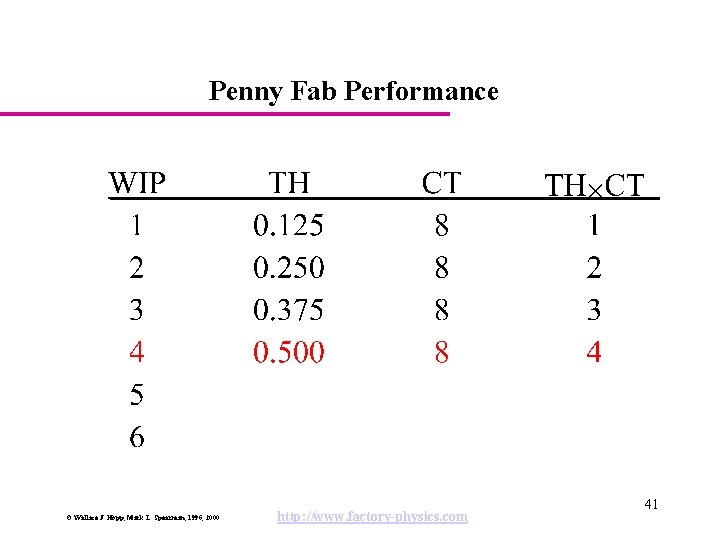
Penny Fab Performance © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 41

The Penny Fab (WIP=5) Time = 0 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 42

The Penny Fab (WIP=5) Time = 2 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 43

The Penny Fab (WIP=5) Time = 4 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 44

The Penny Fab (WIP=5) Time = 6 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 45

The Penny Fab (WIP=5) Time = 8 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 46

The Penny Fab (WIP=5) Time = 10 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 47

The Penny Fab (WIP=5) Time = 12 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 48

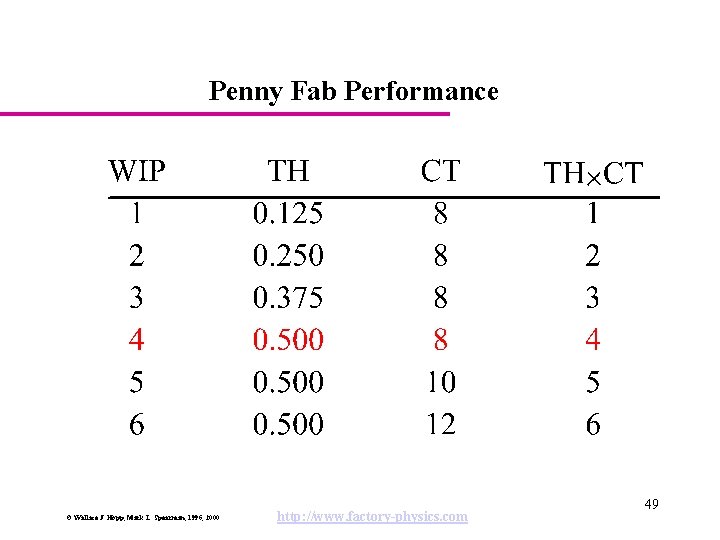
Penny Fab Performance © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 49

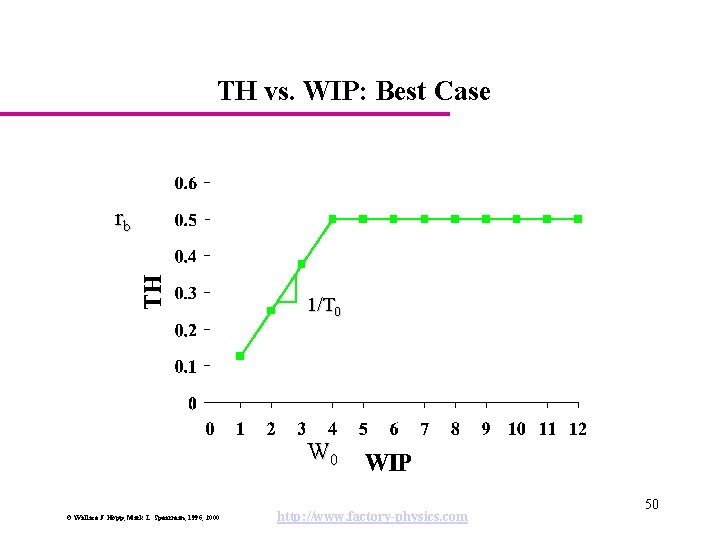
TH vs. WIP: Best Case rb 1/T 0 W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 50

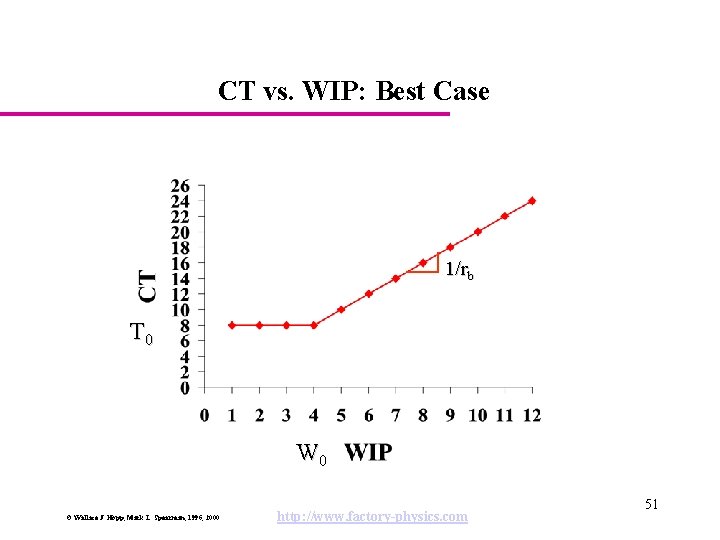
CT vs. WIP: Best Case 1/rb T 0 W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 51

Best Case Performance Best Case Law: The minimum cycle time (CTbest) for a given WIP level, w, is given by The maximum throughput (THbest) for a given WIP level, w is given by, © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 52

Best Case Performance (cont. ) Example: For Penny Fab, rb = 0. 5 and T 0 = 8, so W 0 = 0. 5 8 = 4, which are exactly the curves we plotted. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 53

A Manufacturing Law Little's Law: The fundamental relation between WIP, CT, and TH over the long-term is: Insights: • Fundamental relationship • Simple units transformation • Definition of cycle time (CT = WIP/TH) © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 54

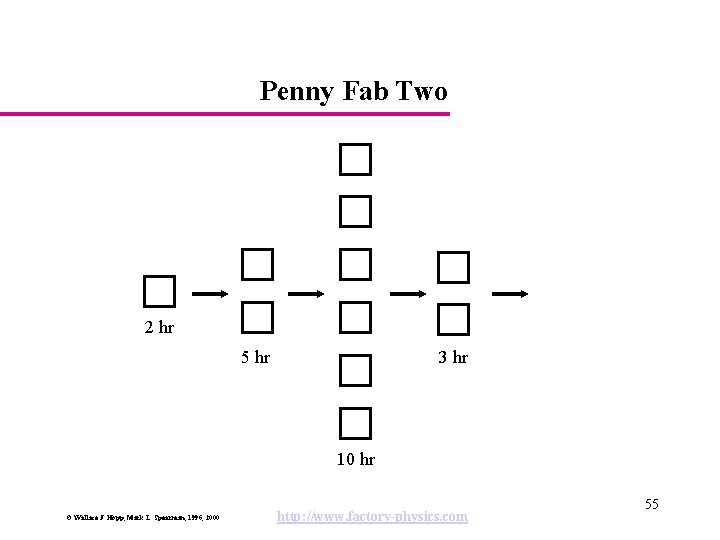
Penny Fab Two 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 55

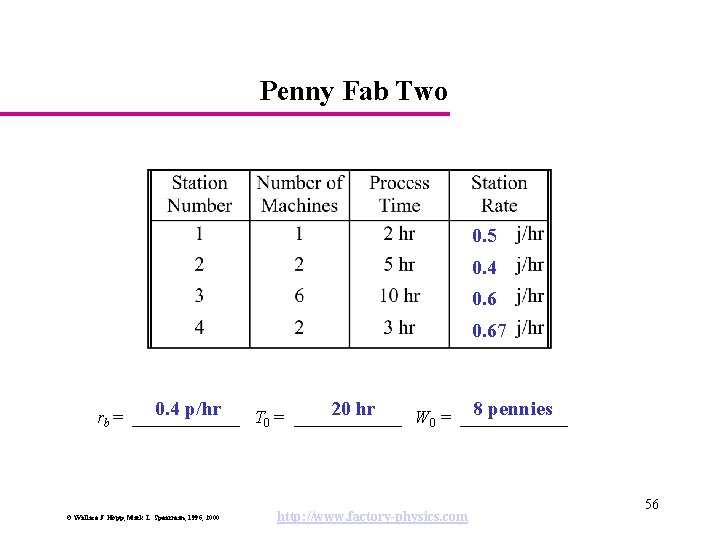
Penny Fab Two 0. 5 0. 4 0. 67 0. 4 p/hr 20 hr 8 pennies rb = ______ T 0 = ______ W 0 = ______ © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 56

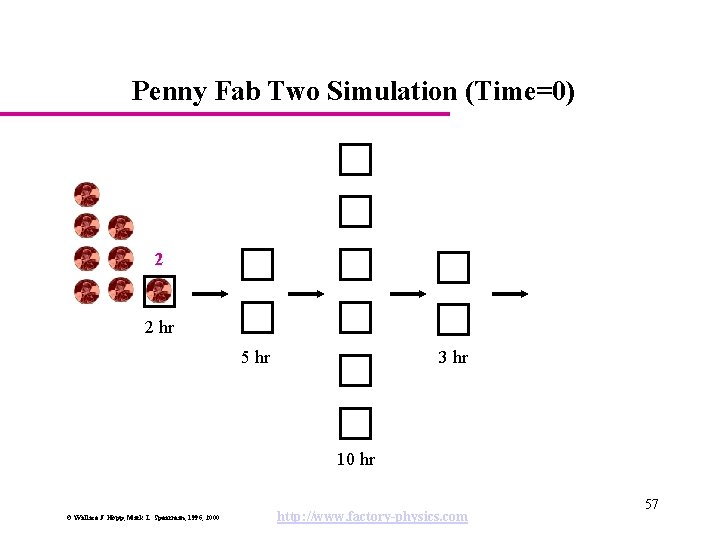
Penny Fab Two Simulation (Time=0) 2 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 57

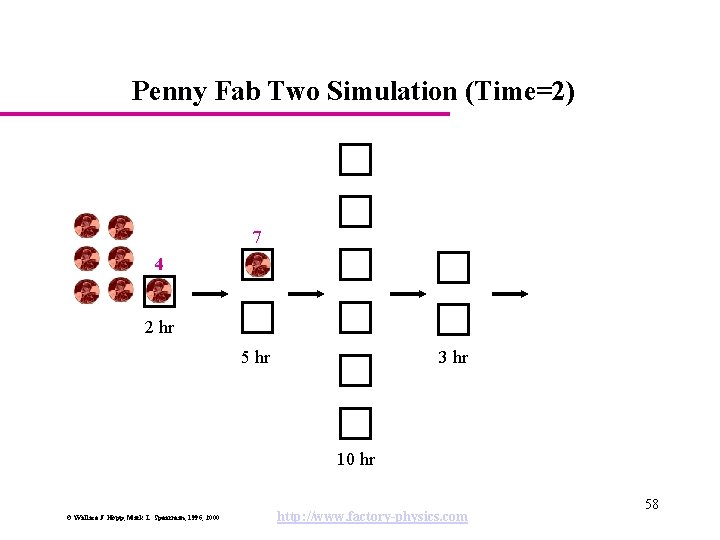
Penny Fab Two Simulation (Time=2) 7 4 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 58

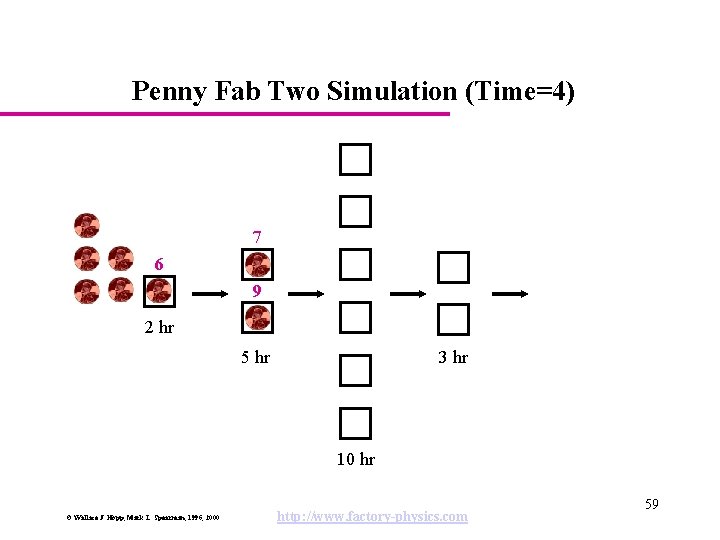
Penny Fab Two Simulation (Time=4) 7 6 9 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 59

Penny Fab Two Simulation (Time=6) 7 8 9 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 60

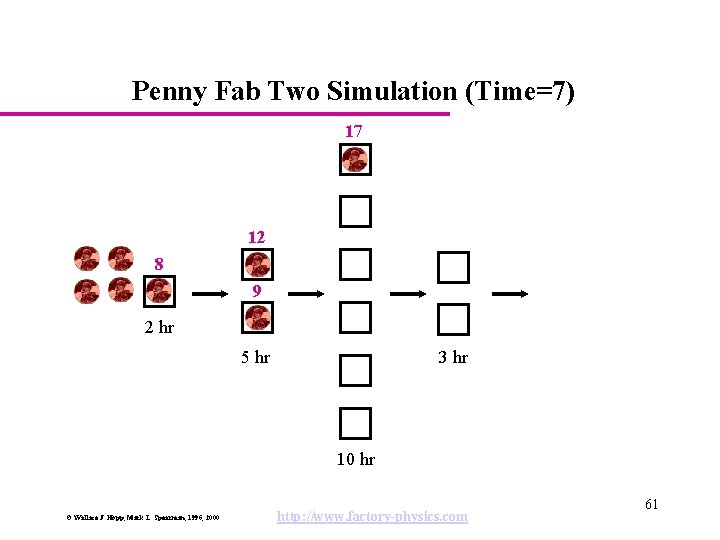
Penny Fab Two Simulation (Time=7) 17 12 8 9 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 61

Penny Fab Two Simulation (Time=8) 17 12 10 9 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 62

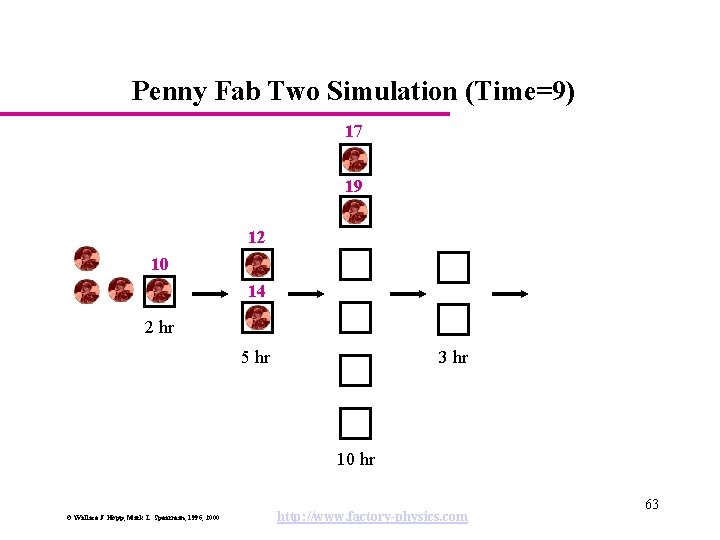
Penny Fab Two Simulation (Time=9) 17 19 12 10 14 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 63

Penny Fab Two Simulation (Time=10) 17 19 12 12 14 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 64

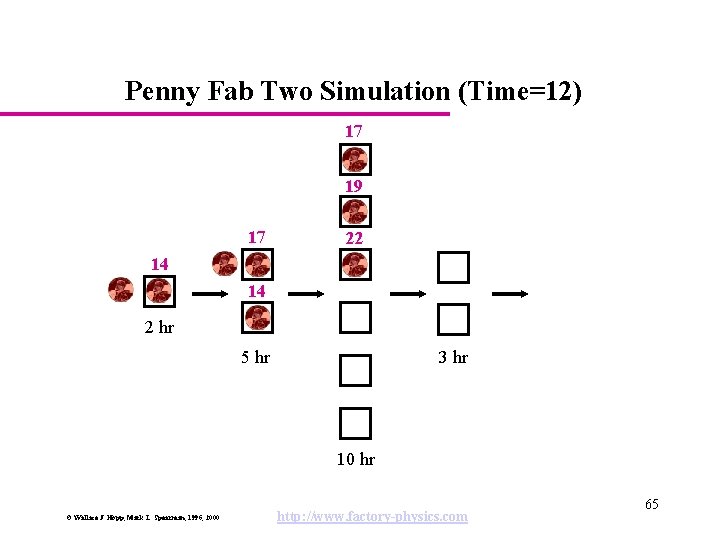
Penny Fab Two Simulation (Time=12) 17 19 17 22 14 14 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 65

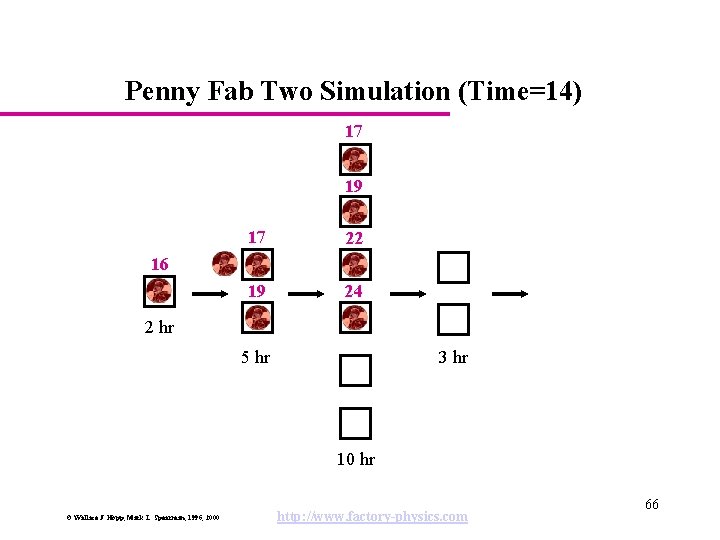
Penny Fab Two Simulation (Time=14) 17 19 17 22 19 24 16 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 66

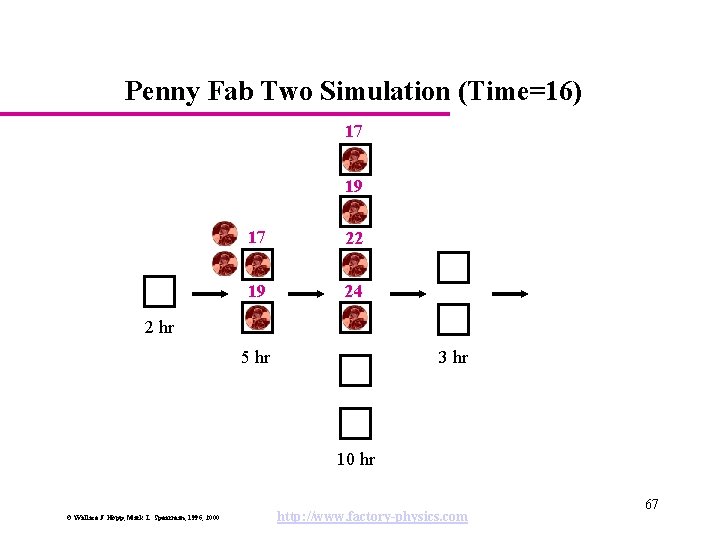
Penny Fab Two Simulation (Time=16) 17 19 17 22 19 24 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 67

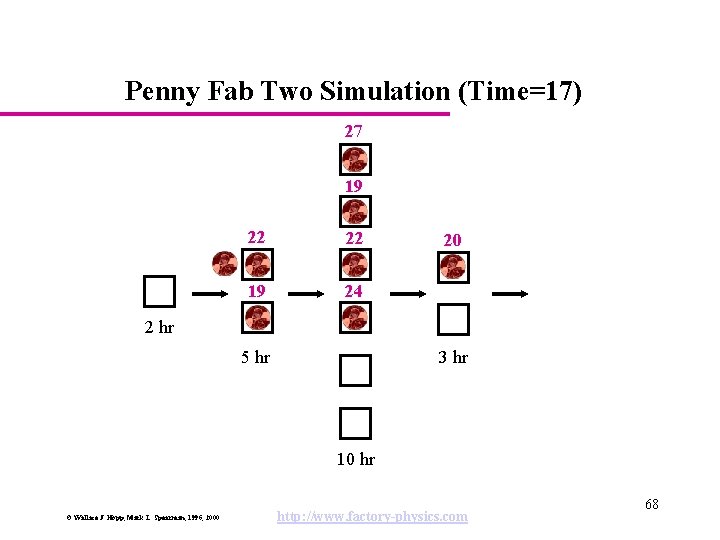
Penny Fab Two Simulation (Time=17) 27 19 22 22 19 24 20 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 68

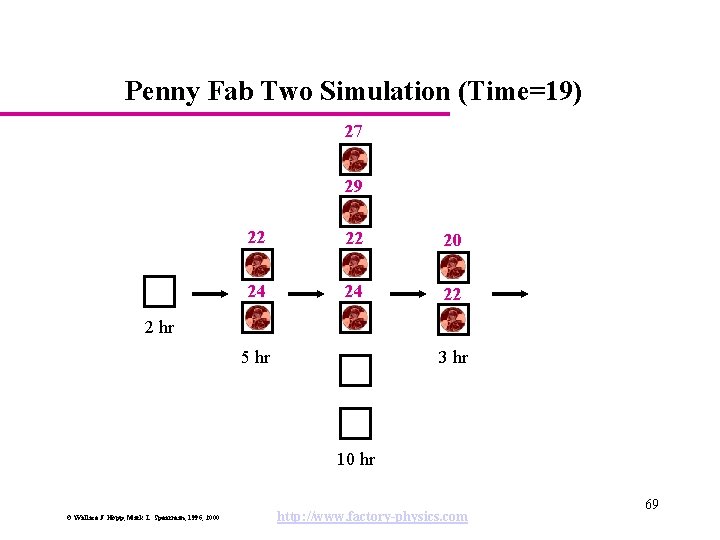
Penny Fab Two Simulation (Time=19) 27 29 22 22 20 24 24 22 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 69

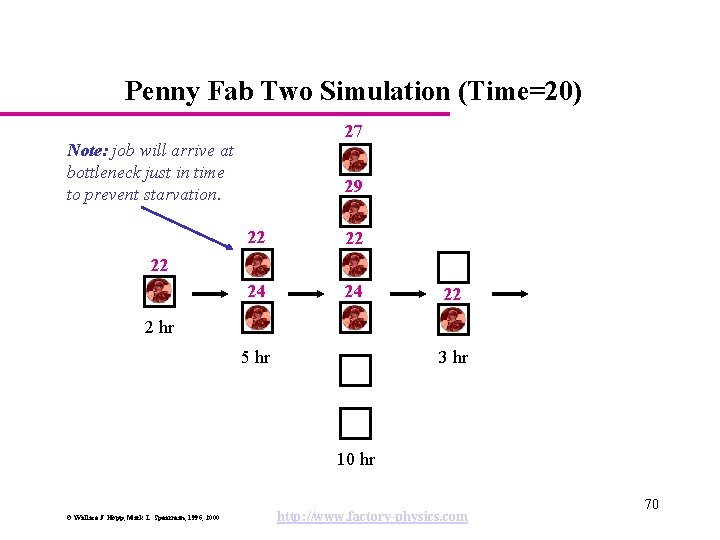
Penny Fab Two Simulation (Time=20) 27 Note: job will arrive at bottleneck just in time to prevent starvation. 29 22 22 24 24 22 22 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 70

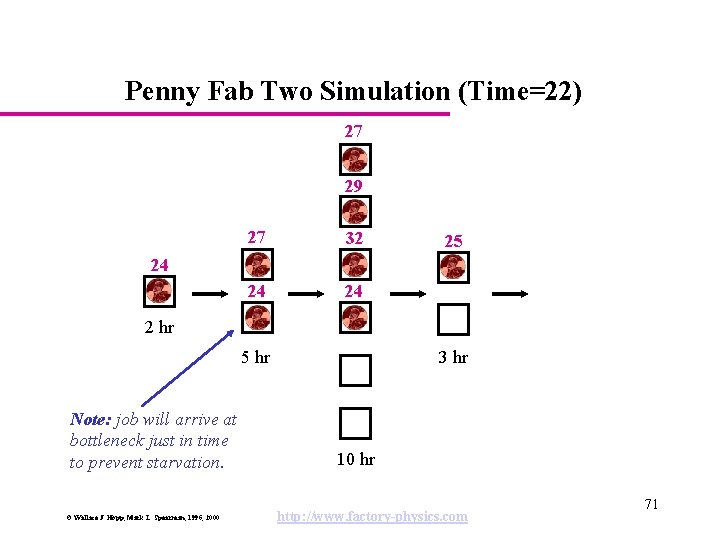
Penny Fab Two Simulation (Time=22) 27 29 27 32 24 24 25 24 2 hr 5 hr Note: job will arrive at bottleneck just in time to prevent starvation. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 3 hr 10 hr http: //www. factory-physics. com 71

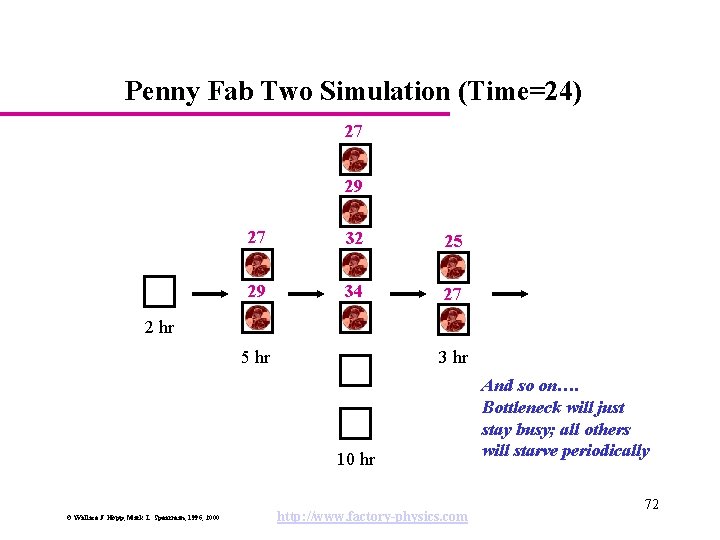
Penny Fab Two Simulation (Time=24) 27 29 27 32 25 29 34 27 2 hr 5 hr 3 hr 10 hr © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com And so on…. Bottleneck will just stay busy; all others will starve periodically 72

Worst Case Observation: The Best Case yields the minimum cycle time and maximum throughput for each WIP level. Question: What conditions would cause the maximum cycle time and minimum throughput? Experiment: • set average process times same as Best Case (so rb and T 0 unchanged) • follow a marked job through system • imagine marked job experiences maximum queueing © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 73

Worst Case Penny Fab Time = 0 hours © Wallace J. Hopp, Mark L.

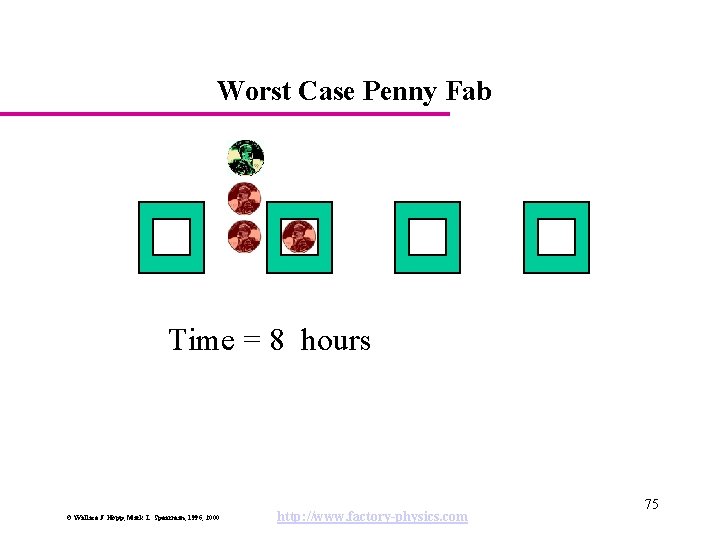
Worst Case Penny Fab Time = 8 hours © Wallace J. Hopp, Mark L.

Worst Case Penny Fab Time = 16 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 76

Worst Case Penny Fab Time = 24 hours © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 77

Worst Case Penny Fab Time = 32 hours Note: CT = 32 hours = 4 8 = w. T 0 TH = 4/32 = 1/8 = 1/T 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 78

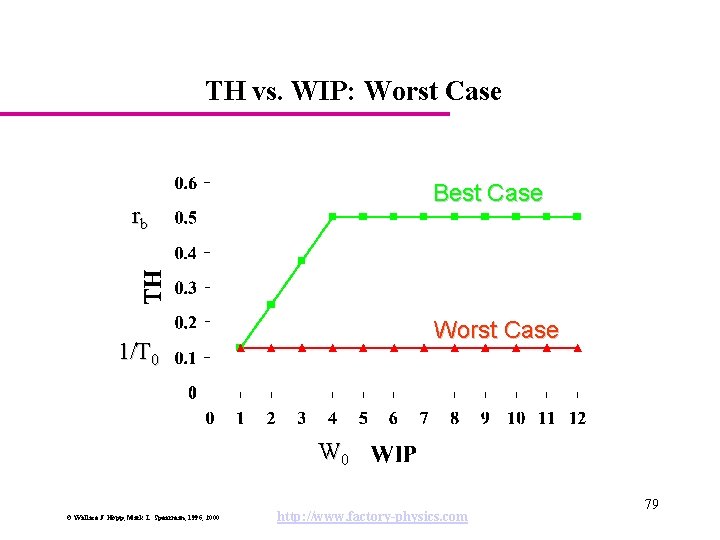
TH vs. WIP: Worst Case Best Case rb Worst Case 1/T 0 W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 79

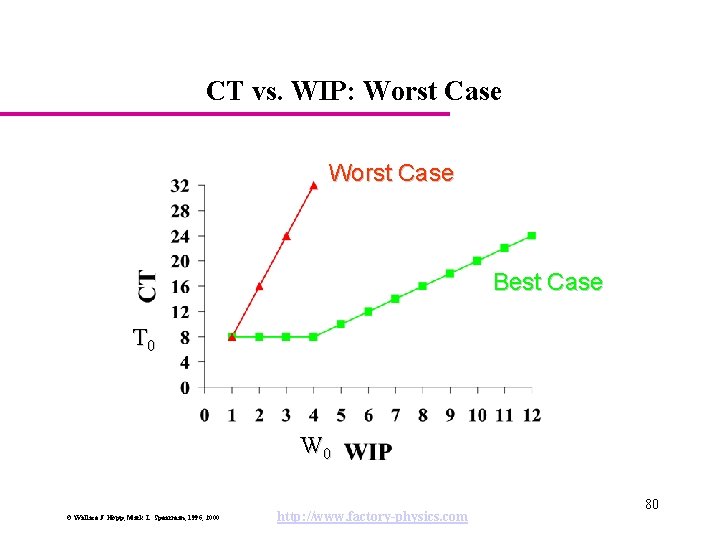
CT vs. WIP: Worst Case Best Case T 0 W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 80

Worst Case Performance Worst Case Law: The worst case cycle time for a given WIP level, w, is given by, CTworst = w T 0 The worst case throughput for a given WIP level, w, is given by, THworst = 1 / T 0 Randomness? None - perfectly predictable, but bad! © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 81

Practical Worst Case Observation: There is a BIG GAP between the Best Case and Worst Case performance. Question: Can we find an intermediate case that: • divides “good” and “bad” lines, and • is computable? Experiment: consider a line with a given rb and T 0 and: • single machine stations • balanced lines • variability such that all WIP configurations (states) are equally likely © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 82

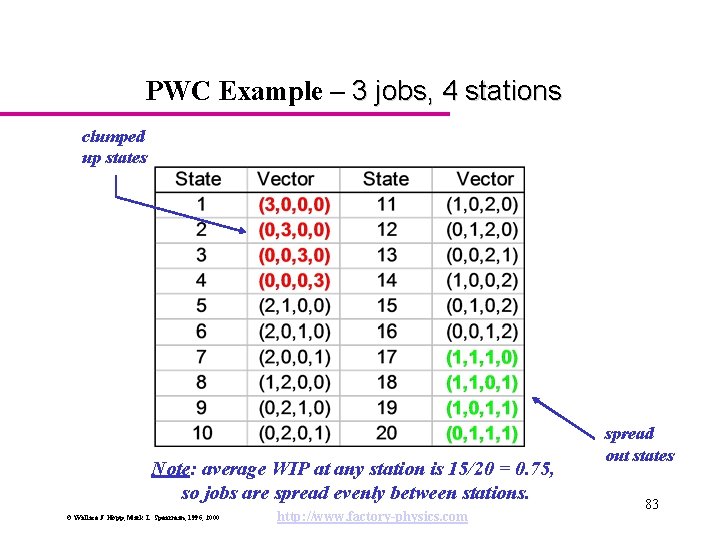
PWC Example – 3 jobs, 4 stations clumped up states Note: average WIP at any station is 15/20 = 0. 75, so jobs are spread evenly between stations. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com spread out states 83

Practical Worst Case Let w = jobs in system, N = no. stations in line, and t = process time at all stations: CT(single) = (1 + (w-1)/N) t CT(line) = N [1 + (w-1)/N] t = Nt + (w-1)t = T 0 + (w-1)/rb TH = WIP/CT = [w/(w+W 0 -1)]rb © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 From Little’s Law http: //www. factory-physics. com 84

Practical Worst Case Performance Practical Worst Case Definition: The practical worst case (PWC) cycle time for a given WIP level, w, is given by, The PWC throughput for a given WIP level, w, is given by, where W 0 is the critical WIP. © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 85

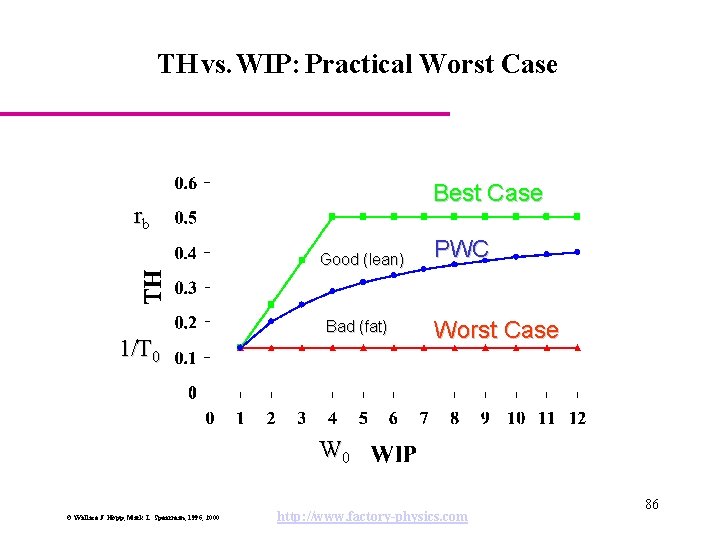
TH vs. WIP: Practical Worst Case Best Case rb Good (lean) 1/T 0 Bad (fat) PWC Worst Case W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 86

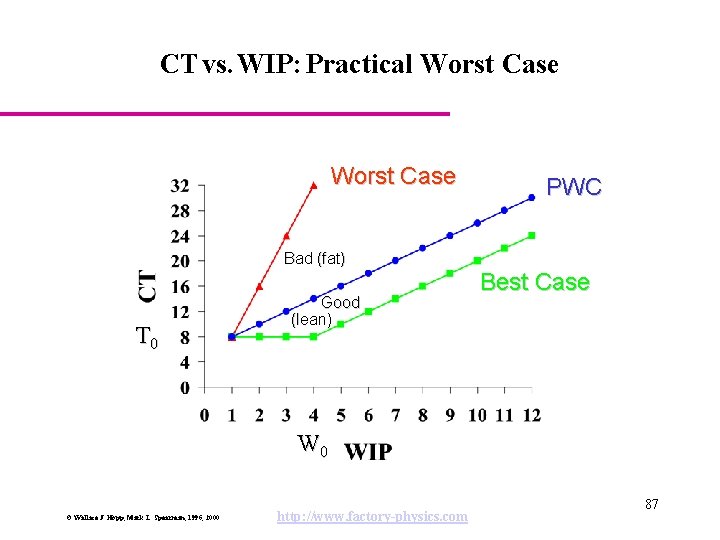
CT vs. WIP: Practical Worst Case PWC Bad (fat) T 0 Good (lean) Best Case W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 87

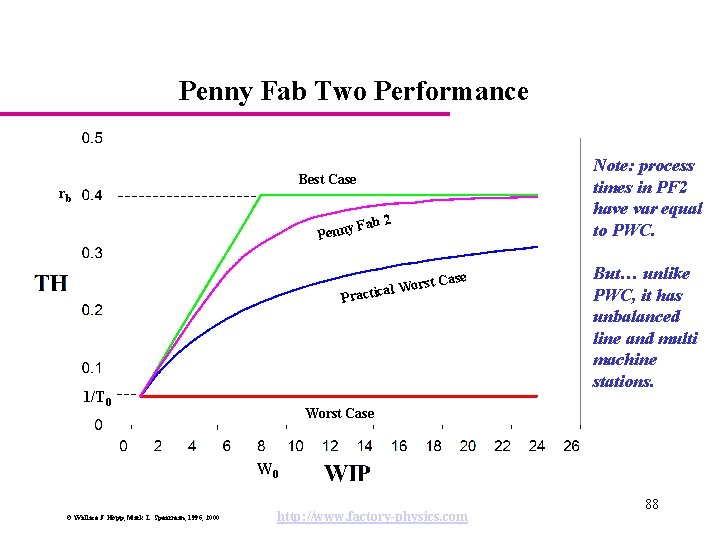
Penny Fab Two Performance Best Case rb Penny Fab 2 e rst Cas o W l a ic Pract 1/T 0 Note: process times in PF 2 have var equal to PWC. But… unlike PWC, it has unbalanced line and multi machine stations. Worst Case W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 88

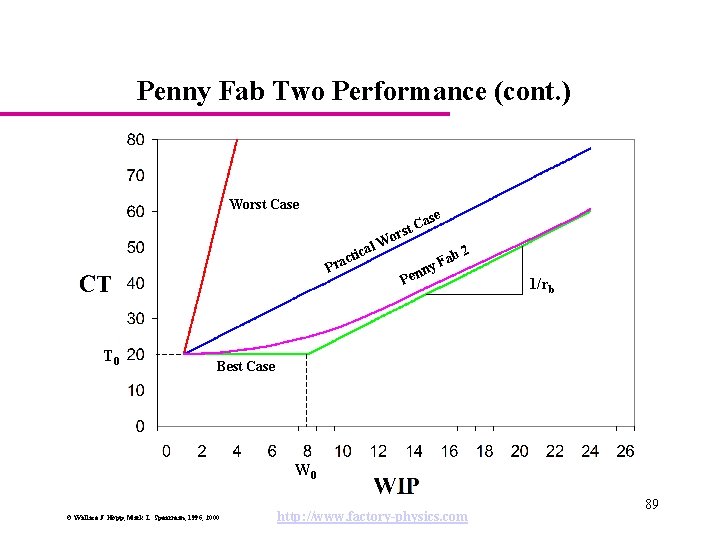
Penny Fab Two Performance (cont. ) Worst Case C rst o l. W a c i ct Pra T 0 ab y. F 2 n Pen 1/rb Best Case W 0 © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 89

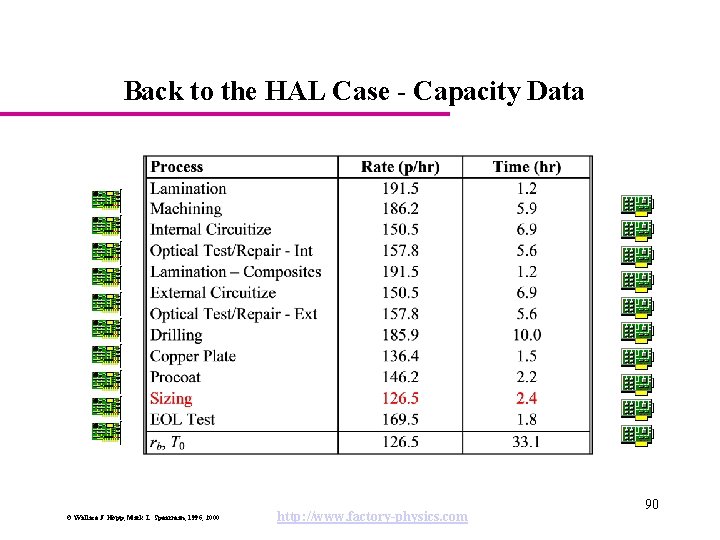
Back to the HAL Case - Capacity Data © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 90

HAL Case - Situation Critical WIP: W 0 = rb. T 0 = 126. 5 33. 9 = 4, 187 Actual Values: • CT = 34 days = 816 hours (at 24 hr/day) • WIP = 37, 000 panels • TH = 45. 8 panels/hour Conclusions: • Throughput is 36% of capacity • WIP is 15 times critical WIP • CT is 24. 6 times raw process time © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 91

HAL Case - Analysis Much higher than actual TH! TH Resulting from PWC with WIP = 47, 600? WIP Required for PWC to Achieve TH = 0. 63 rb? Much lower than actual WIP! Conclusion: actual system is much worse than PWC! © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 92

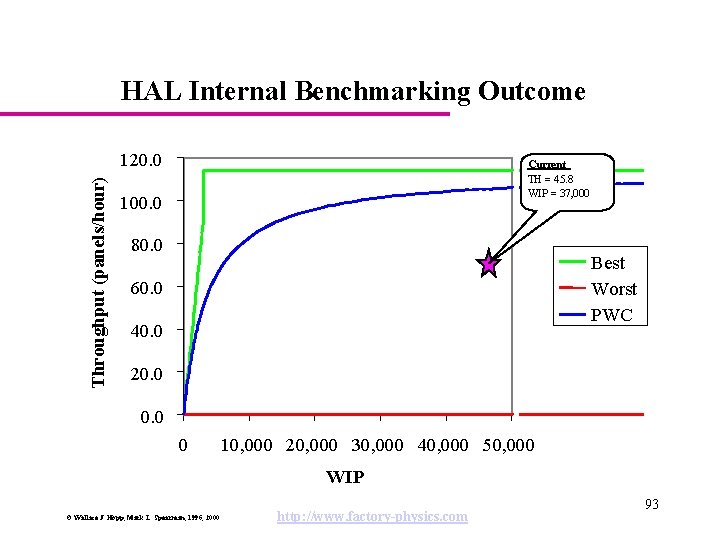
HAL Internal Benchmarking Outcome Throughput (panels/hour) 120. 0 “Lean" Region 100. 0 Current TH = 45. 8 WIP = 37, 000 80. 0 60. 0 “Fat" Region 40. 0 Best Worst PWC 20. 0 0 10, 000 20, 000 30, 000 40, 000 50, 000 WIP © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 93

Labor Constrained Systems Motivation: performance of some systems are limited by labor or a combination of labor and equipment. Full Flexibility with Workers Tied to Jobs: • WIP limited by number of workers (n) • capacity of line is n/T 0 • Best case achieves capacity and has workers in “zones” • ample capacity case also achieves full capacity with “pick and run” policy © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 94

Labor Constrained Systems (cont. ) Full Flexibility with Workers Not Tied to Jobs: • TH depends on WIP levels • THCW(n) TH(w) THCW(w) • need policy to direct workers to jobs (focus on downstream is effective) Agile Workforce Systems • bucket brigades • kanban with shared tasks • worksharing with overlapping zones • many others © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 95

Factory Dynamics Takeaways Performance Measures: • throughput • WIP • cycle time • service Range of Cases: • best case • practical worst case • worst case Diagnostics: • simple assessment based on rb, T 0, actual WIP, actual TH • evaluate relative to practical worst case © Wallace J. Hopp, Mark L. Spearman, 1996, 2000 http: //www. factory-physics. com 96