BASIC ENGINEERING SCIENCE CHAPTER 3 FORCE AND MOTION

BASIC ENGINEERING SCIENCE SUBTOPICS • Newton’s Law • Force From Newton’s Law

BASIC ENGINEERING SCIENCE NEWTON’S LAW Sir Isaac Newton (1643 – 1727) English physicist, mathematician, astronomer, natural philosopher, and alchemist

BASIC ENGINEERING SCIENCE NEWTON’S FIRST LAW n. Definition- An object at rest will remain at rest, or if it is moving, it will continue to move with constant velocity, unless acted upon by a resultant force/ an unbalanced force. (Fnet=0) Another way of stating this law in more detail is: 1. If an object is motionless, it will stay motionless unless acted upon by some force. 2. If an object is moving at a constant speed or velocity, it will continue at that speed unless acted upon by some force along the line of motion. 3. If an object is moving, it will move in a straight line unless acted upon at an angle by some force. The Law of Inertia assumes there is no friction or other resistive force that can slow down an object. Inertia can be best demonstrated in outer space.

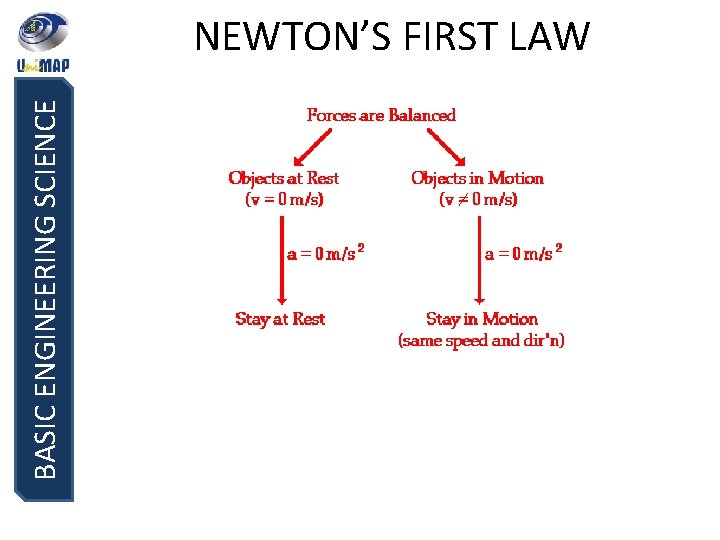
BASIC ENGINEERING SCIENCE NEWTON’S FIRST LAW

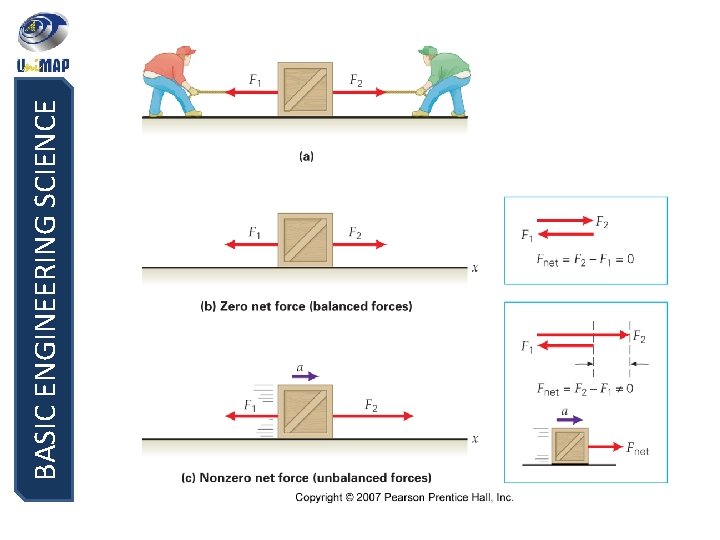
BASIC ENGINEERING SCIENCE Balanced and Unbalanced Force Balanced Force (zero net force) - the net force is zero when forces of equal magnitude act in opposite direction Example : Fnet= F 1 -F 2=0 F 1 F 2

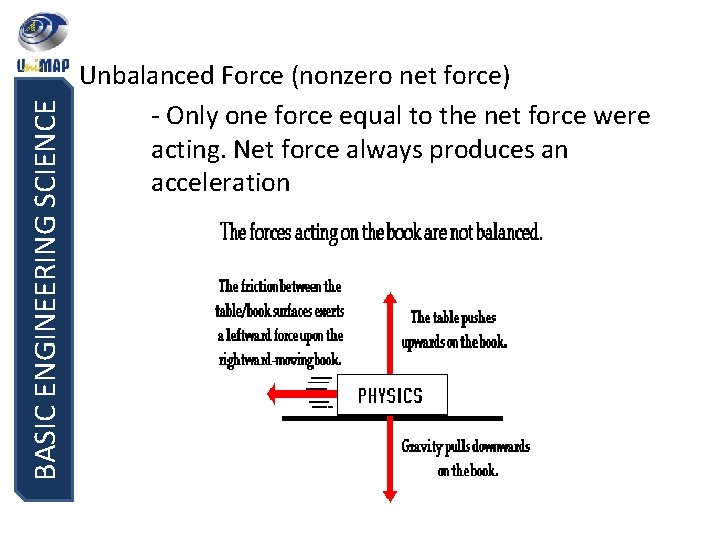
BASIC ENGINEERING SCIENCE Unbalanced Force (nonzero net force) - Only one force equal to the net force were acting. Net force always produces an acceleration Eg: a)

BASIC ENGINEERING SCIENCE

BASIC ENGINEERING SCIENCE NEWTON’S SECOND LAW Definition: The rate of change of momentum of an object is directly proportional to the resultant force acting on the object and is in the same direction as the resultant force. Resultant force, F = d/dt (mv) Where m is the mass and v is velocity We can express the equation; where the net force is equal to the product of the mass times the acceleration SI unif of force: newton (N) or kgms-2

BASIC ENGINEERING SCIENCE NEWTON’S SECOND LAW Figure above shows the relationship among force, acceleration and mass (assuming no friction) Note: If the net force acting on a object is zero, the object’s acceleration is zero, and it remains at rest or in uniform motion Newton's first law. For a nonzero net force(an unbalance force), the resulting acceleration is in the same direction as the force

BASIC ENGINEERING SCIENCE MASS AND WEIGHT Mass and weight are different in physics. Example: Your mass doesn’t change when you go to the moon, but your weight does. Mass shows the quantity, and weight shows the size of gravity. If you know your mass, you can easily find your weight because When the object is drop, it falls towards the earth. Force is acting on the object, its weight (w) is the net force, acceleration due to gravity (g). Therefore equation for weight in terms of mass is a form of Newton second law.

BASIC ENGINEERING SCIENCE The Second Law in Component Form ØA force may be expressed in component notation in 2 dimension : and

BASIC ENGINEERING SCIENCE Newton’s Third Law Definition: Every action has a reaction that is equal in magnitude but opposite in direction In symbol notation, Newton’s third law is : the force exert on object 1 by object 2 : the equal and opposite force exert on object 2 by object 1 (minus indicates opposite direction)

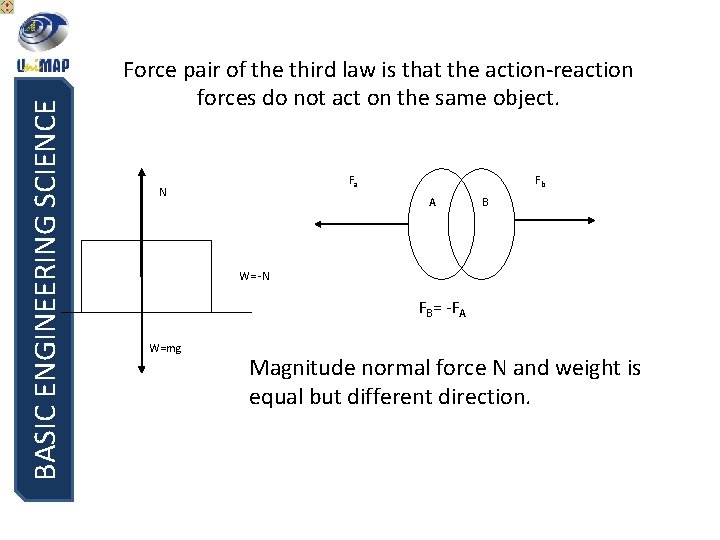
BASIC ENGINEERING SCIENCE Force pair of the third law is that the action-reaction forces do not act on the same object. Fa N Fb A B W= -N FB= -FA W=mg Magnitude normal force N and weight is equal but different direction.

BASIC ENGINEERING SCIENCE When you kick the wall in your room, you will probably end up hurting your foot. WHY? ? ?

BASIC ENGINEERING SCIENCE SUBTOPICS • Newton’s Law • Force From Newton’s Law

BASIC ENGINEERING SCIENCE FORCE FROM NEWTON’S LAW NORMAL FORCE A book on the table exerts a force which is equal to its weight, mg on the table top. R mg Newton’s third law – the table top exerts an equal and opposite force, R on the book. R=mg (opposite direction) The force R (normal reaction) that the table top exerts on the book is normal, or perpendicular to the table top.

NORMAL FORCE is the force exerted by a surface, and is BASIC ENGINEERING SCIENCE perpendicular to the surface R Fg θ Friction mg sin θ θ A θ mg cos θ mg The normal reaction R is not necessarily always equals to the weight, mg of the object Figure above shows the box at rest on a rough plane inclined at an angle θ to the horizontal. The weight mg of the box may be resolved into two orthogonal directions. One component, mg sin θ, is parallel to the inclined plane and another component, mg cos θ, is perpendicular to the inclined plane. Since the box is not moving; R= mg cos θ and friction, Fg =mg sin θ

BASIC ENGINEERING SCIENCE FORCE FROM NEWTON’S LAW FRICTIONAL FORCE Frictional Forces are divided to 2 conditions: a)Static Friction- exist when the object is static/before motion occurs b)Kinetic Friction- exist when the object is moving. Static Friction-is the resistance to motion that occurs between contacting surfaces

BASIC ENGINEERING SCIENCE STATIC FRICTION N A book resting on a flat table, the frictional force is zero. There is no force trying to move the book across the table, so there is no need for a frictional force because there is nothing for the frictional force to oppose. P F W If we try to slide the book across the table, however, friction will come in to play. Let's say it takes a force of 5 N to start the book moving. If we push on the book with a force of less than 5 N, the book won't move, because the frictional force will exactly balance the force we apply. If we push with a 1 N force, a 1 N frictional force opposes us. If we exert a 2 N force, the frictional force matches us at 2 N, and so on. When a frictional force exists but there is no relative motion of the surfaces in contact (e. g. , the book isn't sliding across the table), we call it a static frictional force, Fs. The static frictional force is given by the equation: µs = coefficient of static friction

BASIC ENGINEERING SCIENCE KINETIC FRICTION What happens when one object is sliding over another, when there is relative motion between two surfaces? There will still be a frictional force, but because we're dealing with things in motion we call it the kinetic frictional force. There is a different coefficient of friction associated with kinetic friction, the kinetic coefficient of friction, which is always less than or equal to the static coefficient. As with the static frictional force, the kinetic frictional force acts to oppose the relative motion of the surfaces in contact. One important difference between the two is that the kinetic friction equation has an equals sign: the kinetic force of friction is always equal to the kinetic coefficient of friction times the normal force. µk = coefficient of kinetic friction

BASIC ENGINEERING SCIENCE EXAMPLE 8 Given: Coefficient of static friction between the 40 kg box and the floor is 0. 650. a) What is the minimum horizontal force must the worker pull to get the box moving? b) If the worker maintain the force once the box starts to move and coefficient of kinetic friction between the surface is 0. 500, what is the magnitude of the acceleration of the box?

BASIC ENGINEERING SCIENCE EXAMPLE 9 An applied force of 20 N is used to accelerate an object to the right across a frictional surface. The object encounters 10 N of friction. Use the diagram to determine the normal force, the net force, the coefficient of friction (µ) between the object and the surface, the mass, and the acceleration of the object. (Neglect air resistance. )

BASIC ENGINEERING SCIENCE EXAMPLE 10 A box is pulled at a constant speed of 0. 40 m/s across a frictional surface. Perform an extensive analysis of the diagram below to determine the values for the blanks.

BASIC ENGINEERING SCIENCE EXAMPLE 11 The free-body diagram shows the forces acting upon a 100 -kg crate which is sliding down an inclined plane. The plane is inclined at an angle of 30 degrees. The coefficient of friction between the crate and the incline is 0. 3. Determine the net force and acceleration of the crate.