BASIC ENGINEERING SCIENCE CHAPTER 2 DESCRIPTION OF MOTION

BASIC ENGINEERING SCIENCE CHAPTER 2 DESCRIPTION OF MOTION AND MOTION IN TWO DIMENSION

BASIC ENGINEERING SCIENCE OBJECTIVES • Ability to understand define scalar and vector quantity. • Ability to understand the concept of vector addition, subtraction & components and applying the analytical component method. • Ability to understand distinguish between speed, velocity and acceleration • Ability to apply motion equation based on physical situations.

BASIC ENGINEERING SCIENCE SUBTOPICS • Scalars & Vectors • Speed, Velocity & Acceleration • Motion Equation

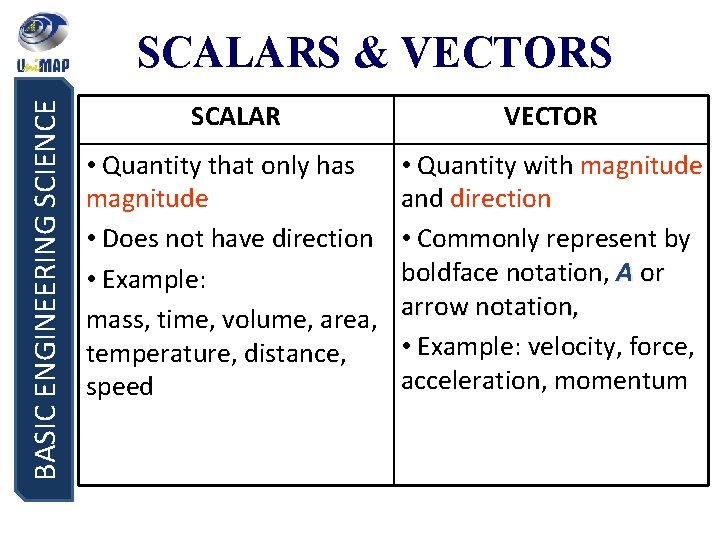
BASIC ENGINEERING SCIENCE SCALARS & VECTORS SCALAR VECTOR • Quantity that only has magnitude • Does not have direction • Example: mass, time, volume, area, temperature, distance, speed • Quantity with magnitude and direction • Commonly represent by boldface notation, A or arrow notation, • Example: velocity, force, acceleration, momentum

BASIC ENGINEERING SCIENCE VECTORS • Vectors – an arrow is commonly used to represent a vector quantity; moreover, there are two common ways to symbolize a vector quantity : – Boldface notation: A – “Arrow” notation: A A=A

BASIC ENGINEERING SCIENCE VECTORS 2 vectors are the same if : (a) magnitude a = magnitude b |a| = |b| (b) a and b parallel or same direction

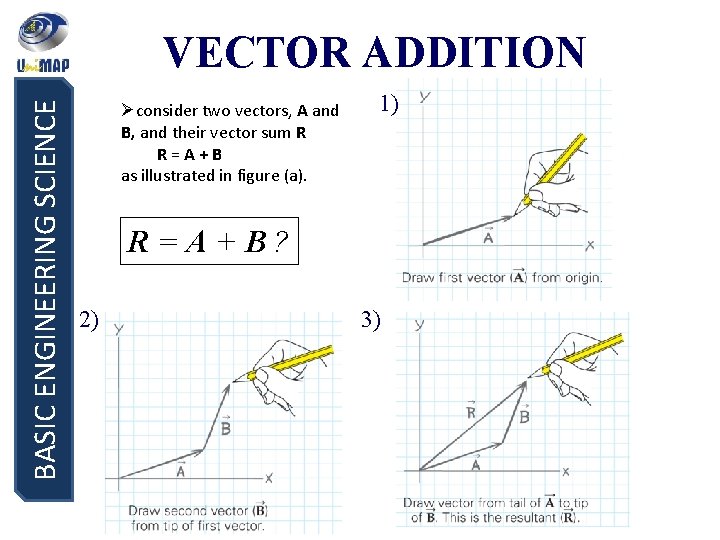
BASIC ENGINEERING SCIENCE VECTOR ADDITION Øconsider two vectors, A and B, and their vector sum R R=A+B as illustrated in figure (a). 1) R=A+B? 2) 3)

BASIC ENGINEERING SCIENCE the sum of vectors is independent of the order in which the vectors are added, as long as we maintain their length and direction

BASIC ENGINEERING SCIENCE VECTORS SUBSTRACTION R = A – B = A + (–B) The –ve of a vector is represented by an arrow of the same length as the original vector, but pointing in the opposite direction (A+B) B A R=(A-B) -B

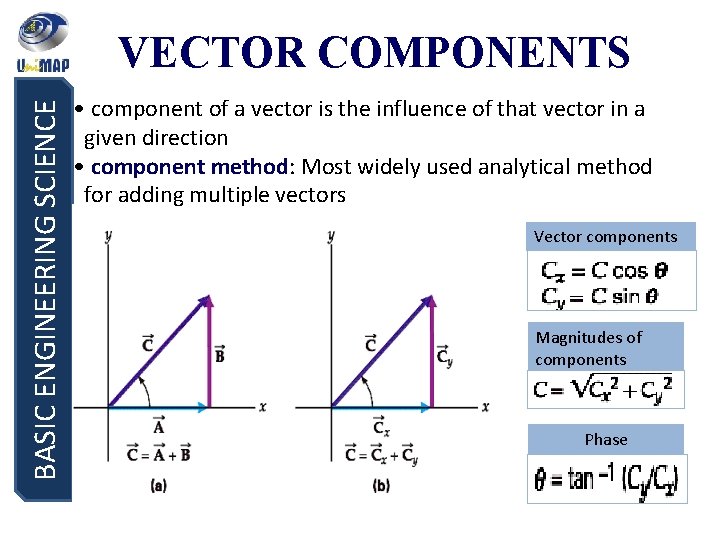
BASIC ENGINEERING SCIENCE VECTOR COMPONENTS • component of a vector is the influence of that vector in a given direction • component method: Most widely used analytical method for adding multiple vectors Vector components Magnitudes of components Phase

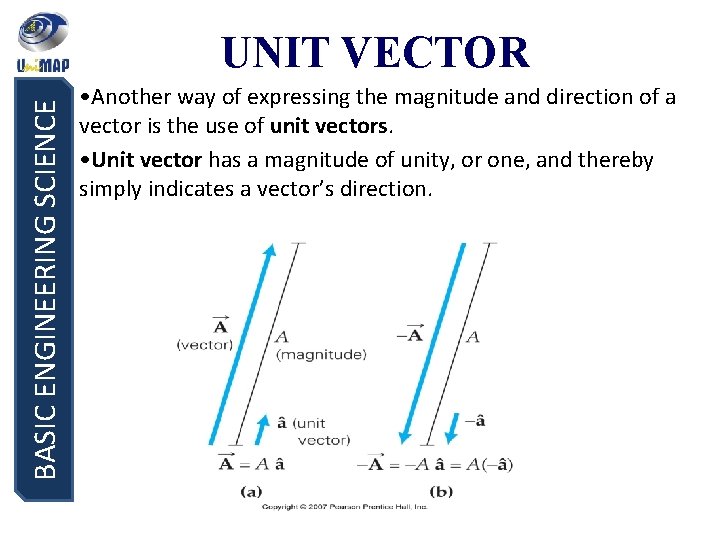
BASIC ENGINEERING SCIENCE UNIT VECTOR • Another way of expressing the magnitude and direction of a vector is the use of unit vectors. • Unit vector has a magnitude of unity, or one, and thereby simply indicates a vector’s direction.

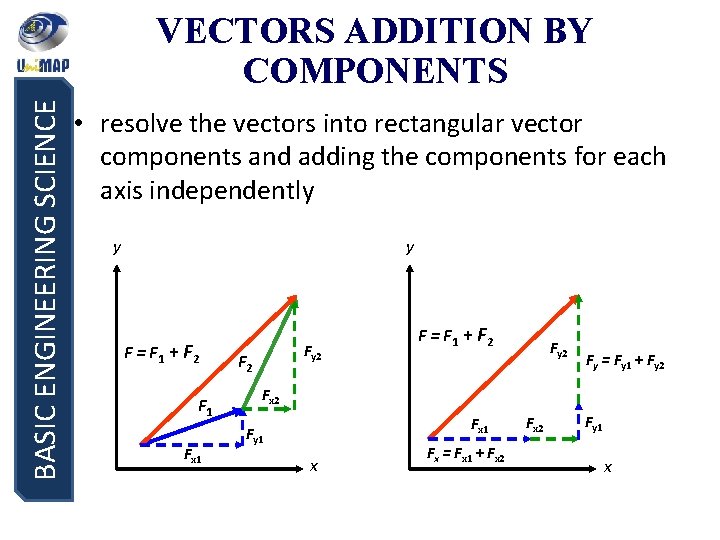
BASIC ENGINEERING SCIENCE VECTORS ADDITION BY COMPONENTS • resolve the vectors into rectangular vector components and adding the components for each axis independently y y F = F 1 + F 2 F 1 Fx 1 Fy 2 F = F 1 + F 2 Fy = Fy 1 + Fy 2 Fx 1 Fy 1 x Fx = Fx 1 + Fx 2 Fy 1 x

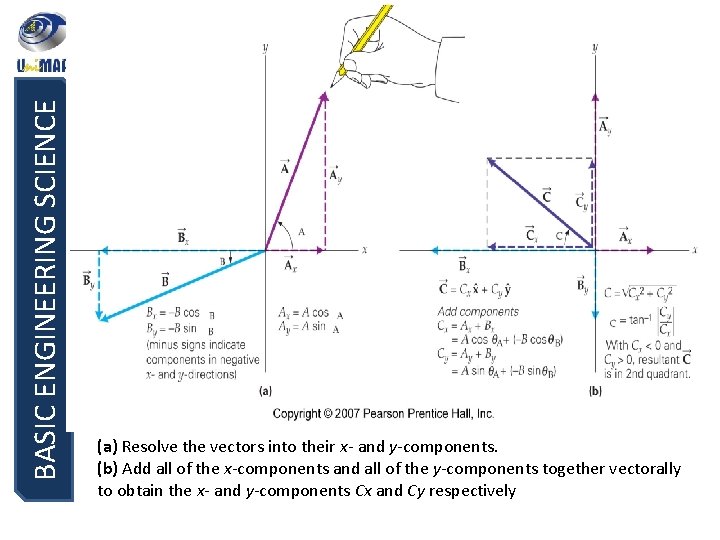
BASIC ENGINEERING SCIENCE (a) Resolve the vectors into their x- and y-components. (b) Add all of the x-components and all of the y-components together vectorally to obtain the x- and y-components Cx and Cy respectively

BASIC ENGINEERING SCIENCE EXAMPLE 1 Given V 1 = 4. 5 m/s V 2 = 5. 0 m/s Find the vector v(resultant) V 3 = 9. 0 m/s

BASIC ENGINEERING SCIENCE SOLUTION (a) Resolve the vectors into their x- and y-components. X-component Y-component (b) Add all of the x-components and all of the y-components together vectorally

BASIC ENGINEERING SCIENCE In component form, the resultant vector is In magnitude-angle form, the resultant velocity has a magnitude of Magnitude Phase

BASIC ENGINEERING SCIENCE EXAMPLE 2 You are given two displacement vectors: 1) A with magnitude of 6. 0 m in the direction of 45 o below the + x-axis, and 2) B, which has an x – component of +2. 5 m and a y-component of +4. 0 m. Find a vector C so that A + B + C equals a vector D that has magnitude of 6. 0 m in the + y-direction.

BASIC ENGINEERING SCIENCE SOLUTION x - components y - components Ax = Ay = Bx = By = Cx = Cy = Dx =

BASIC ENGINEERING SCIENCE • Calculate x – and y – components separately: x-components: y-components: • So, C = _______ x + _______y Magnitude: Phase:

BASIC ENGINEERING SCIENCE SUBTOPICS • Scalars & Vectors • Speed, Velocity & Acceleration • Motion Equation

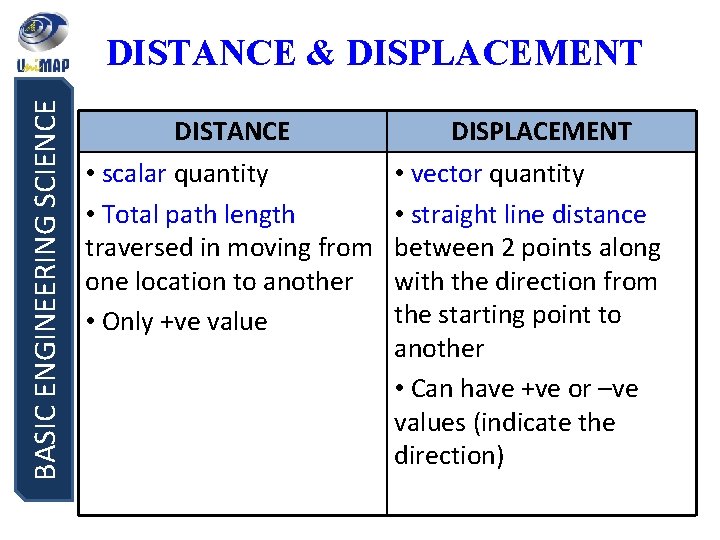
BASIC ENGINEERING SCIENCE DISTANCE & DISPLACEMENT DISTANCE • scalar quantity • Total path length traversed in moving from one location to another • Only +ve value DISPLACEMENT • vector quantity • straight line distance between 2 points along with the direction from the starting point to another • Can have +ve or –ve values (indicate the direction)

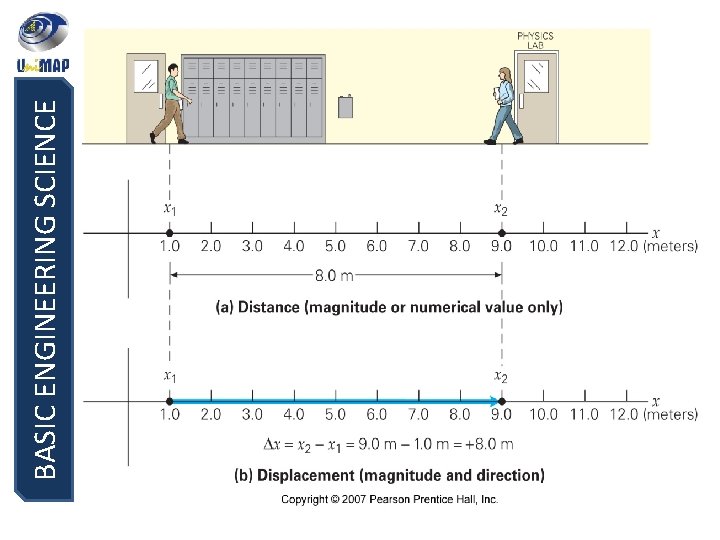
BASIC ENGINEERING SCIENCE

BASIC ENGINEERING SCIENCE SPEED & VELOCITY SPEED § refers to how fast an object is moving § scalar quantity § defined as the rate of motion, or rate of change in position. §fast moving = high speed, slow moving = slow speed § zero speed = no movement VELOCITY §Refers to how fast something is moving and in which direction it is moving. § vector quantity § defined as the rate of change of displacement or the rate of displacement. § velocity = 0, does not mean the object is not moving.

BASIC ENGINEERING SCIENCE SPEED SI Unit: m/s VELOCITY SI Unit: m/s

BASIC ENGINEERING SCIENCE EXAMPLE 3 A jogger jogs from one end to the other of a straight 300 m track in 2. 50 min and then jogs back to the starting point in 3. 30 min. What was the jogger’s average velocity (a) in jogging to the far end of the track (b) coming back to the starting point, and (c) for total jog 2. 5 minutes 300 m 3. 3 minutes

BASIC ENGINEERING SCIENCE SOLUTION

BASIC ENGINEERING SCIENCE Find the jogger’s average speed for each cases in this example and compare it with respective average volocities. [Will the average speed for (c) be zero?

BASIC ENGINEERING SCIENCE ACCELERATION - rate of change of velocity. SI Unit: meters per second squared (m/s 2). Since velocity is a vector quantity, with magnitude and direction, an acceleration can occur when a) A change in magnitude, but not direction b) A change in direction, but not magnitude c) A change in both, magnitude and direction

BASIC ENGINEERING SCIENCE SI Unit: meters per second squared (m/s 2).

BASIC ENGINEERING SCIENCE EXAMPLE 4 A couple of sport-utility vehicle (SUV) are traveling at 110 km/h on a PLUS highway. The drives sees an accident in the distance and slows down to 55 km/h in 10 s. What is the average acceleration of the SUV?

BASIC ENGINEERING SCIENCE SOLUTION

Signs of Velocity and Acceleration +x BASIC ENGINEERING SCIENCE -x a positive v positive RESULT : a negative v positive RESULT : a positive v negative RESULT : a negative v negative RESULT :

BASIC ENGINEERING SCIENCE SUBTOPICS • Scalars & Vectors • Speed, Velocity & Acceleration • Motion Equation

BASIC ENGINEERING SCIENCE What is motion? • In physics, motion means a continuous change in the position of a body relative to a reference point, as measured by a particular observer in a particular frame of reference. MOTION EQUATION • Equation that describe the behavior of system (e. g the motion of a particle under an influence of a force) as a function of time • Sometimes the term refers to the differential equations that the system satisfies and sometimes to the solutions to those equations.

BASIC ENGINEERING SCIENCE Motion With Constant Acceleration When an object moves along the straight line and velocity increase uniformly from Vo to v in time t. Therefore the constant acceleration is given by: constant acceleration: a = change in velocity / time taken = (v-u )/ t v = u+at

BASIC ENGINEERING SCIENCE derivation of motion equation: • v = u + at • s = ½(u+v)t • Where ; s = the distance traveled from the initial state to the final state (displacement) u = the initial speed v = the final speed • s = ut + ½ at 2 • v 2 = u 2 + 2 as a = the constant acceleration t = the time taken to move from the initial state to the final state

BASIC ENGINEERING SCIENCE EXAMPLE 5 • The speed of a car travelling along a straight road decreases uniformly from 12 m/s to 8 m/s over 88 m. Calculate the a) Decelaration of the car b)Time taken for the speed to decrease from 12 m/s to 8 m/s c) Time taken for the car to come to a halt from the speed of 12 m/s d)Total distance travelled by the car during this time.

BASIC ENGINEERING SCIENCE SOLUTION

BASIC ENGINEERING SCIENCE EXAMPLE 6 A drag racer starting from rest accelerates in a straight line at a constant rate of 5. 5 m/s 2 for 6. 0 s. a) What is the racer’s velocity at the end of this period of time? b) If a parachute deployed at this time cause the racer to slow down uniformly a rate of 25 m/s 2, how long it will take the racer to come to a stop? c) What is the racer’s instantaneous velocity 10 seconds after the parachute is deployed?

BASIC ENGINEERING SCIENCE SOLUTION

BASIC ENGINEERING SCIENCE FREE FALL MOTION • Objects in motion solely under the influence of gravity. • Acceleration due to gravity, represent by the symbol g (value assume 9. 81 ms-2) • Expressing a = -g in the kinematics equation for constant acceleration in the y-direction yields the following; v = u - gt s = ut - ½ gt 2 v 2 = u 2 - 2 gs

BASIC ENGINEERING SCIENCE FREE FALL MOTION a= -9. 8 m/s 2 a= a= 2 -9. 8 m/s 2 Acceleration § Acceleration due to gravity is always downward, then it is in negative y-direction. § The ball’s acceleration stays the same – on the way up, at the top, and on the way back down. It’s always negative. Velocity § When the ball ascending, the velocity decrease to zero. § The velocity of the ball is zero when the ball reaches the highest point. § Magnitude of velocity starts increase when the ball fall downwards. § But the velocity of ball is negative because it’s moving downward

BASIC ENGINEERING SCIENCE EXAMPLE 7 A boy on a bridge throws a stone vertically downward with an initial velocity of 14. 7 m/s toward the river below. If the stone hits the water 2. 00 s later, what is the height of the bridge above the water? How much longer would it take for the stone to reach the river if the boy had dropped the ball rather than thrown it?

BASIC ENGINEERING SCIENCE SOLUTION

BASIC ENGINEERING SCIENCE EXAMPLE 8 A tennis ball is dropped from a height of 2. 0 m and it rebounds to a height of 1. 5 m. If the ball is in contact with the floor for 0. 010 s, what is the acceleration of the ball when it is in contact with the floor?

BASIC ENGINEERING SCIENCE SOLUTION