Basic Electricity and Electronics Module Two Basic Electronics

Transistor Basics n A semiconductor device n Conductivity is controlled by current n Made

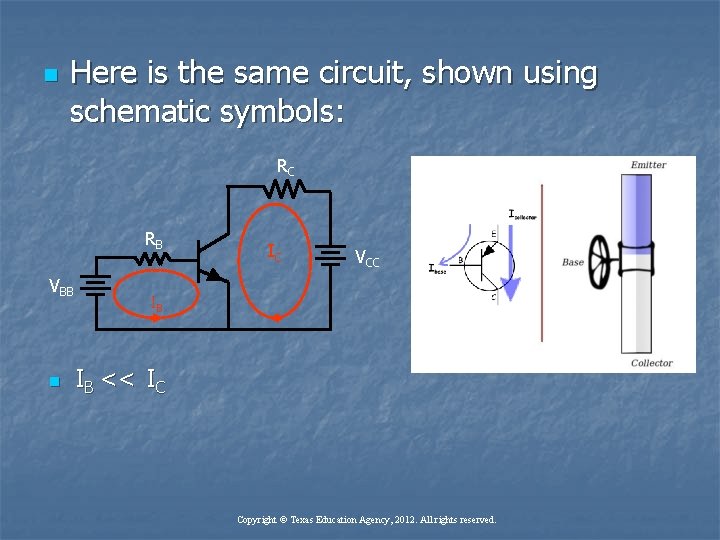
n Here is the same circuit, shown using schematic symbols: RC RB VBB n

n Here is the same circuit, shown slightly different: Power Supply (VCC) RC Output Signal In n n This is a standard transistor switch Used in computers and other electronic devices Copyright © Texas Education Agency, 2012. All rights reserved.

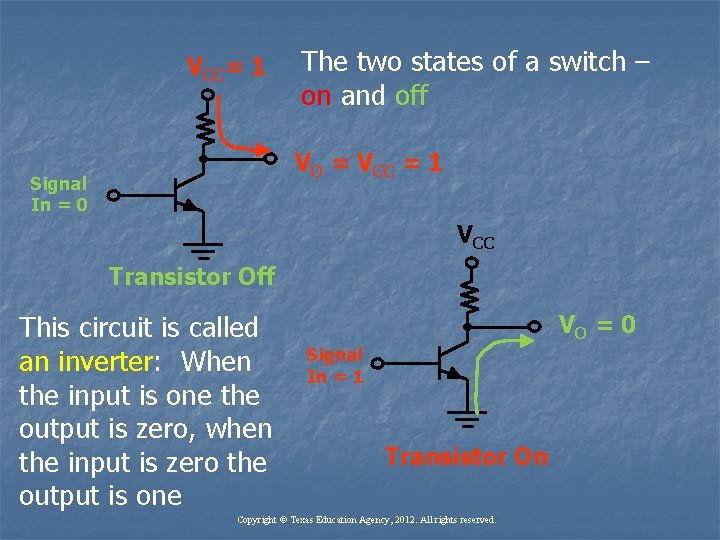
VCC= 1 The two states of a switch – on and off VO = VCC = 1 Signal In = 0 VCC Transistor Off This circuit is called an inverter: When the input is one the output is zero, when the input is zero the output is one VO = 0 Signal In = 1 Transistor On Copyright © Texas Education Agency, 2012. All rights reserved.

We Use Transistors n n n All logic uses transistors We use voltage to represent binary TTL (transistor – transistor logic) is common: + 5 V = binary 1 n 0 V = binary 0 n n These voltages will turn on or off transistors Copyright © Texas Education Agency, 2012. All rights reserved.

The Truth Table A tool used to understand binary logic n Shows every possible input n Shows the output for each input n What circuit does this represent? Input Output A X 0 1 1 0 An Inverter! Copyright © Texas Education Agency, 2012. All rights reserved.

Binary Logic n n n A set of rules that applies to a digital circuit Logic defines the way the circuit will act Given a set of inputs, the output will produce a specific outcome Always acts exactly the same way We use a truth table to help us define how we want the logic circuit to act Copyright © Texas Education Agency, 2012. All rights reserved.

Two Bit Binary Adder Adds two binary bits n Binary can only have two values, 0 and 1 n 0 +0 0 n 0 +1 1 1 +0 1 1 +1 0 Carry 1 1 + 1 = 2, which is not valid binary Copyright © Texas Education Agency, 2012. All rights reserved.

Truth Table for Binary Addition We have two inputs n We generate two outputs n Input Output Carry Σ (sum) Co A B How do we do this? 0 0 1 1 0 1 0 1 1 0 0 1 Copyright © Texas Education Agency, 2012. All rights reserved. First, we have to understand binary!

Binary Numbers n n n Binary only has two values, 0 and 1 The decimal number system has ten values, 0 through 9 How do we count higher than 9 in decimal? n n -We add decimal places How do we count higher than one in binary? n -We add binary bits Copyright © Texas Education Agency, 2012. All rights reserved.

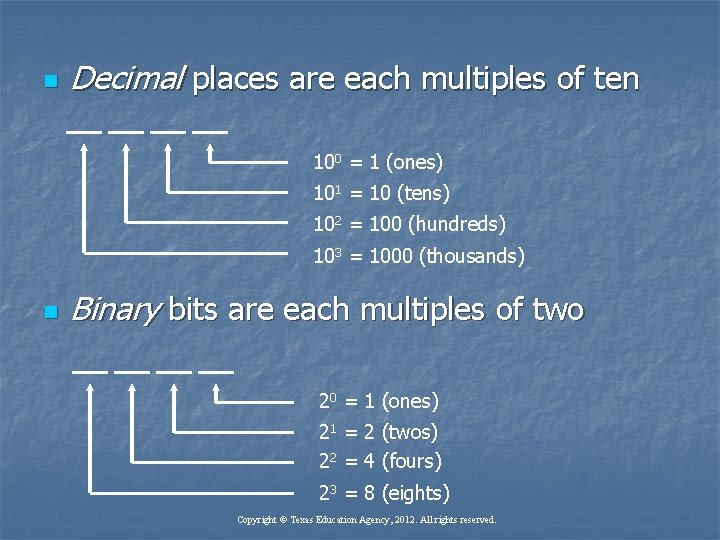
n Decimal places are each multiples of ten 100 = 1 (ones) 101 = 10 (tens) 102 = 100 (hundreds) 103 = 1000 (thousands) n Binary bits are each multiples of two 20 = 1 (ones) 21 = 2 (twos) 22 = 4 (fours) 23 = 8 (eights) Copyright © Texas Education Agency, 2012. All rights reserved.

Reading Binary Numbers n A decimal number like 9437 reads: n n Nine thousand, four hundred, thirty, seven. The binary number 1011 has values: One eight, no fours, one two, one. n 1011 has a decimal value of 11 (eleven) n n How do read the binary 1111? n n Decimal Fifteen How do you count higher than fifteen? n Add more binary bits (decimal places) Copyright © Texas Education Agency, 2012. All rights reserved.

Binary Bit Values n To count up to 1000 (decimal) you need ten binary bits Bit number 9 8 7 6 5 4 3 2 1 0 Decimal value 5 1 2 2 5 6 1 2 8 6 4 3 2 1 6 8 4 2 1 n To count higher, you need more binary bits Copyright © Texas Education Agency, 2012. All rights reserved.

Binary to Decimal n The binary number: 1001011001 n Has a decimal value: 512 + 64 + 16 + 8 + 1 = 601 1 0 0 1 n 9 8 7 6 5 4 3 2 1 0 5 1 2 2 5 6 1 2 8 6 4 3 2 1 6 8 4 2 1 This process involves addition Copyright © Texas Education Agency, 2012. All rights reserved.

Decimal to Binary n n Decimal to binary is a little harder The process involves subtraction For example, consider the decimal number: 361 Go back to the binary count: 9 8 7 6 5 4 3 2 1 0 5 1 2 2 5 6 1 2 8 6 4 3 2 1 6 8 4 2 1 Copyright © Texas Education Agency, 2012. All rights reserved.

Binary Count n n The easiest way to show all possible input values is a binary count Keep adding one to the previous value Everyone should be able to count in binary D = 1, C = 2, B = 4, A=8 A B C D Deci Hex 0 0 0 0 1 1 1 1 0 0 1 1 Copyright © Texas Education Agency, 2012. All rights reserved. 0 1 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F

A B C D Deci What happens if you have to keep counting? 0 0 0 1 1 1 Hex 0 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 0 1 1 1 16 17 31 255 10 11 1 F FF Copyright © Texas Education Agency, 2012. All rights reserved.

Hexadecimal n n n Computers and electronic devices communicate in binary All those 1’s and 0’s are confusing Is there an easy way to tell what the binary values are? YES – it’s called Hexadecimal is a base 16 number system Hexadecimal exactly represents 4 binary bits Copyright © Texas Education Agency, 2012. All rights reserved.

Using Hex n n To create hex, start with bit 0 and group the binary number into groups of 4 For example, our decimal 601 would be: n 10010110012 or 25916 Copyright © Texas Education Agency, 2012. All rights reserved.

Using Hex n n To create hex, start with bit 0 and group the binary number into groups of 4 For example, our decimal 601 would be: n 10 0101 10012 or 25916 Copyright © Texas Education Agency, 2012. All rights reserved.

Using Hex n n To create hex, start with bit 0 and group the binary number into groups of 4 For example, our decimal 601 would be: n 70110 = 10 1011 11012 = ? Copyright © Texas Education Agency, 2012. All rights reserved.

Using Hex n n To create hex, start with bit 0 and group the binary number into groups of 4 For example, our decimal 601 would be: n 70110 = 10 1011 11012 = 2 BD 16 Copyright © Texas Education Agency, 2012. All rights reserved.

n There are several ways to indicate the hex number system: n n n Use the subscript 16 Use a lower case h right after the number Use a dollar sign, e. g. $2 BD Hex is a shorthand way of representing binary The hex number always exactly represents 4 binary bits Copyright © Texas Education Agency, 2012. All rights reserved.

Back to Addition n n Add 2 4 -bit binary numbers: 111 0101 5 + 0011 +3 11000 8 1 + 1 = 2, which is written 10 in binary This 1 is a carry into the next bit Copyright © Texas Education Agency, 2012. All rights reserved.

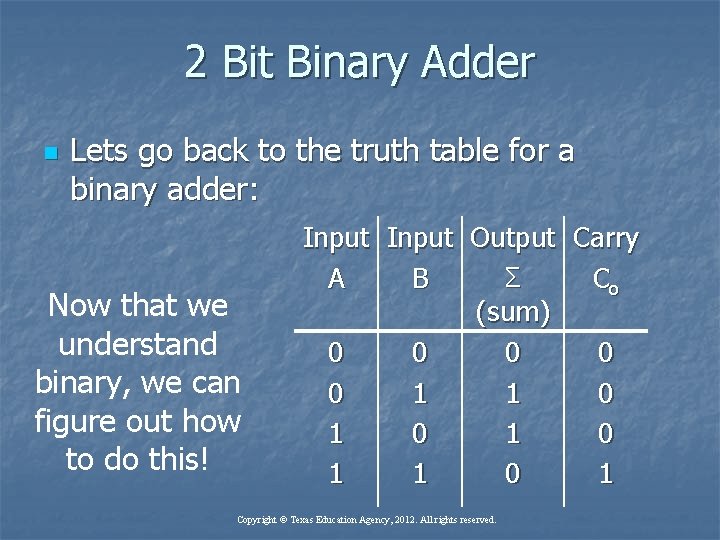
2 Bit Binary Adder n Lets go back to the truth table for a binary adder: Now that we understand binary, we can figure out how to do this! Input Output Carry Σ A B Co (sum) 0 0 0 1 1 0 1 0 1 Copyright © Texas Education Agency, 2012. All rights reserved.