Basic dynamics The equation of motion Scale Analysis

Basic dynamics The equation of motion Scale Analysis Boussinesq approximation Geostrophic balance (Reading: Pond and Pickard, Chapters 6 -8)

The Equation of Motion Newton’s second law in a rotating frame. (Navier-Stokes equation) Force per unit mass : Acceleration relative to axis fixed to the earth. 1 sidereal day =86164 s : Pressure gradient force. 1 solar day = 86400 s : Coriolis force, where : Effective (apparent) gravity. : Friction. g 0=9. 80 m/s 2 molecular kinematic viscosity.

Gravitation and gravity

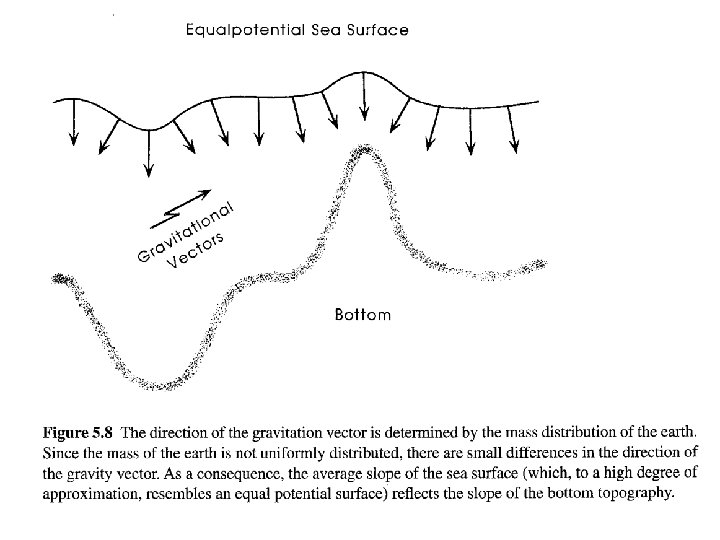
Gravity: Equal Potential Surfaces • g changes about 5% 9. 78 m/s 2 at the equator (centrifugal acceleration 0. 034 m/s 2, radius 22 km longer) 9. 83 m/s 2 at the poles) • equal potential surface normal to the gravitational vector constant potential energy the largest departure of the mean sea surface from the “level” surface is about 2 m (slope 10 -5) • The mean ocean surface is not flat and smooth earth is not homogeneous

Coriolis Force

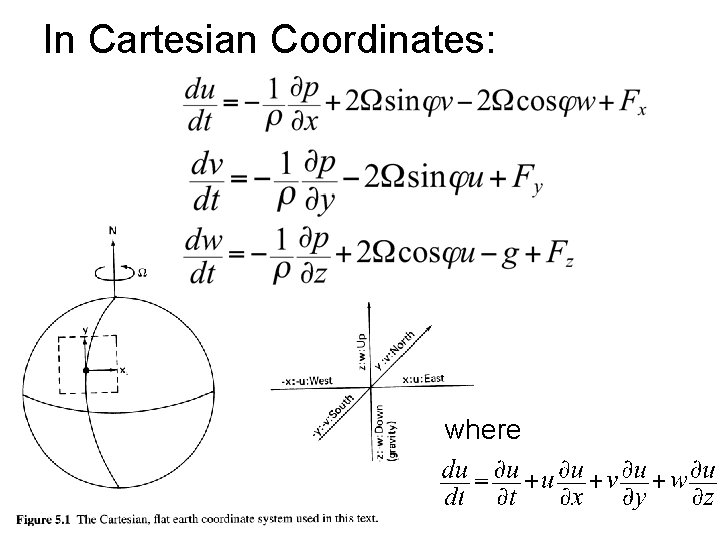
In Cartesian Coordinates: where

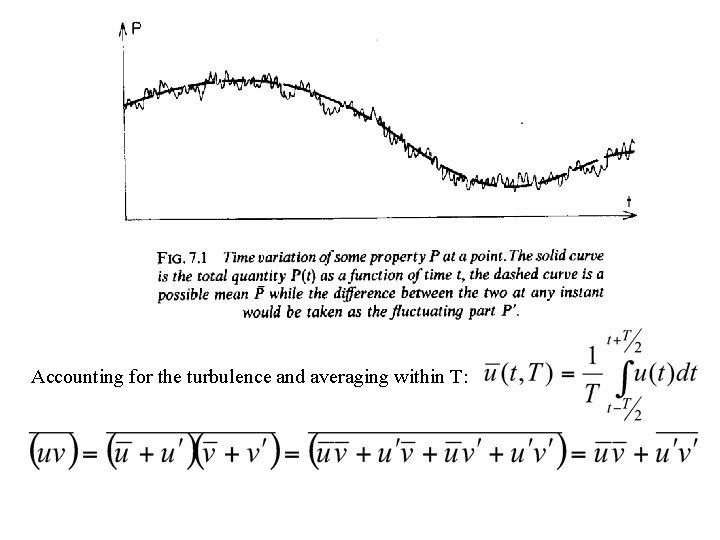
Accounting for the turbulence and averaging within T:

Given the zonal momentum equation If we assume the turbulent perturbation of density is small i. e. , The mean zonal momentum equation is Where Fx is the turbulent (eddy) dissipation If the turbulent flow is incompressible, i. e. ,

Eddy Dissipation , Reynolds stress tensor and eddy viscosity: Then Where the turbulent viscosity coefficients are anisotropic. Ax=Ay~102 -105 m 2/s >> Az ~10 -4 -10 -2 m 2/s

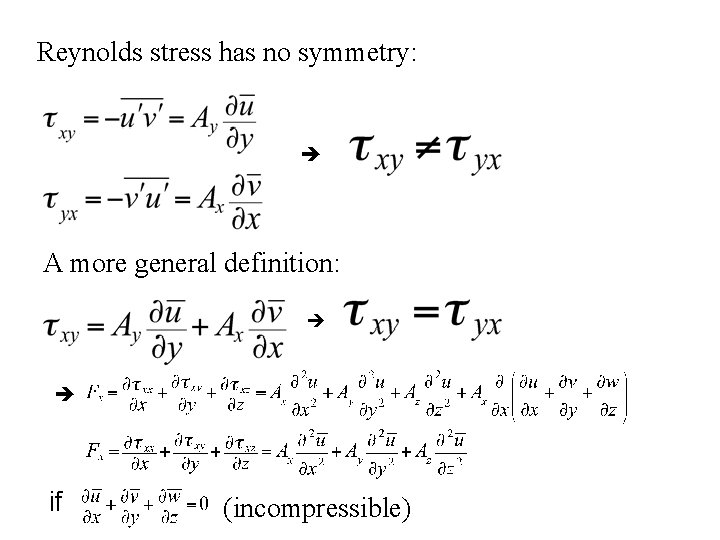
Reynolds stress has no symmetry: A more general definition: if (incompressible)

Scaling of the equation of motion • Consider mid-latitude ( ≈45 o) open ocean away from strong current and below sea surface. The basic scales and constants: L=1000 km = 106 m H=103 m U= 0. 1 m/s T=106 s (~ 10 days) 2 sin 45 o=2 cos 45 o≈2 x 7. 3 x 10 -5 x 0. 71=10 -4 s-1 g≈10 m/s 2 ≈103 kg/m 3 Ax=Ay=105 m 2/s Az=10 -1 m 2/s • Derived scale from the continuity equation Incompressible W=UH/L=10 -4 m/s

Scaling the vertical component of the equation of motion Hydrostatic Equation accuracy 1 part in 106

Boussinesq approximation Density variations can be neglected for its effect on mass but not on weight (or buoyancy). Assume that where , we have neglected

Geostrophic balance in ocean’s interior

Scaling of the horizontal components (accuracy, 1% ~ 1‰) Zero order (Geostrophic) balance Pressure gradient force = Coriolis force

Re-scaling the vertical momentum equation Since the density and pressure perturbation is not negligible in the vertical momentum equation, i. e. , , , and The vertical pressure gradient force becomes

Taking into the vertical momentum equation, we have If we scale , and assume then and (accuracy ~ 1‰)