Basic Data Structures Trees l Informal a tree

Basic Data Structures - Trees l Informal: a tree is a structure that looks like a real tree (upside-down) l Formal: a tree is a connected graph with no cycles.

Trees A tree T is a set of nodes storing values in a parent-child relationship with following properties: l T has a special node called root. l Each node different from root has a parent node. l When there is no node, T is an empty tree.

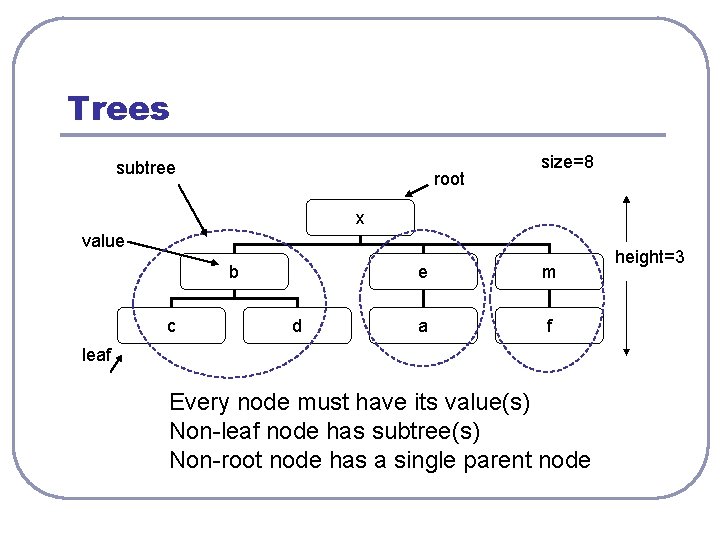
Trees subtree root size=8 x value b c d e m a f leaf Every node must have its value(s) Non-leaf node has subtree(s) Non-root node has a single parent node height=3

Binary Trees l Each node can have at most 2 sub-trees Multi-way Trees (order k) ---------------------------l Each node can have at most k sub-trees

Binary Search Trees A binary search tree is a tree satisfying the following properties: v It is a binary tree. v For every node with a value N, all values in its left sub-tree must less than or equal to N, and all values in its right sub-tree must be greater than or equal to N.

This is NOT a binary search tree 5 4 3 7 2 8 9

Searching in a binary search tree search( s, t ) { If(s==t’s value) return t; If(t is leaf) return null If(s < t’s value) search(s, t’s left tree) else search(s, t’s right tree)} Time per level O(1) h Total O(h)

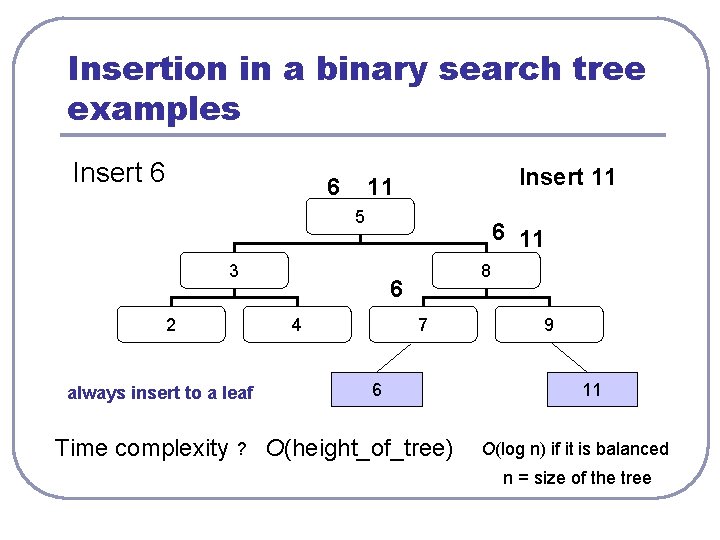
Insertion in a binary search tree examples Insert 6 6 Insert 11 11 5 6 11 3 2 Time complexity 6 4 always insert to a leaf ? 8 7 6 O(height_of_tree) 9 11 O(log n) if it is balanced n = size of the tree

Insertion in a binary search tree insert. In. Order(s, t) { if(t is an empty tree) // insert here return a new tree node with value s else if( s < t’s value) t. left = insert. In. Order(s, t. left) else t. right = insert. In. Order(s, t. right) return t }

Comparison – Insertion in an ordered list insert. In. Order(s, list) { loop 1: search from beginning of list, look for an item >= s loop 2: shift remaining list to its right, start from the end of list insert s } Insert 6 6 2 6 3 6 4 Time complexity? 6 5 7 6 8 9 O(n) n = size of the list

Deleting an item from a list delete. Item(s, list) { loop 1: search from beginning of list, look for an item == s loop 2: shift remaining list to its left } delete 6 6 2 6 3 6 4 Time complexity? 6 5 6 7 8 9 O(n) n = size of the list

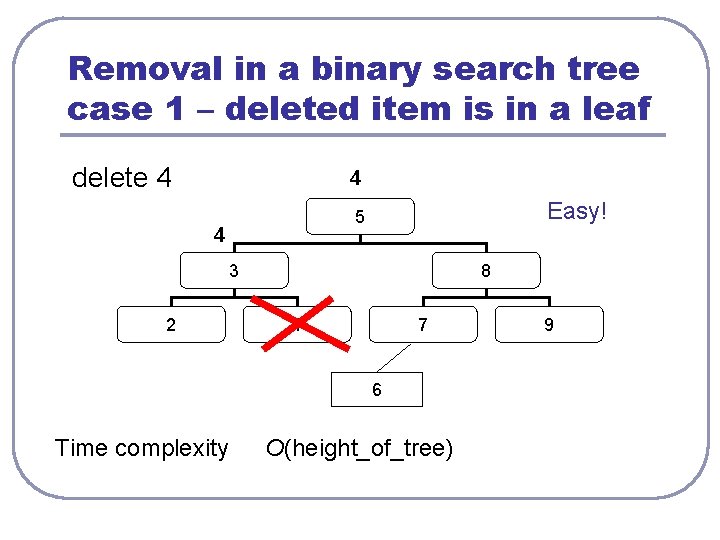
Removal in a binary search tree case 1 – deleted item is in a leaf delete 4 4 Easy! 5 4 3 2 8 4 7 6 Time complexity O(height_of_tree) 9

Removal in a binary search tree case 2 – deleted item is NOT in a leaf delete 5 5 3 2 8 4 7 6 9

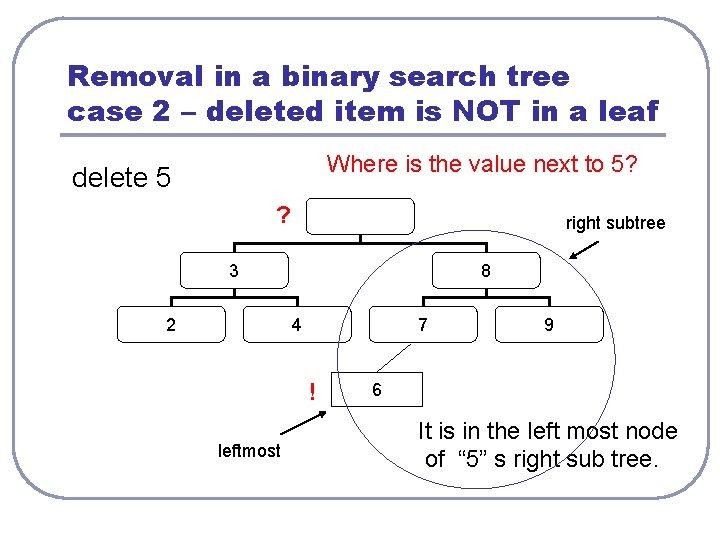
Removal in a binary search tree case 2 – deleted item is NOT in a leaf Where is the value next to 5? delete 5 ? right subtree 3 2 8 4 7 ! leftmost 9 6 It is in the left most node of “ 5” s right sub tree.

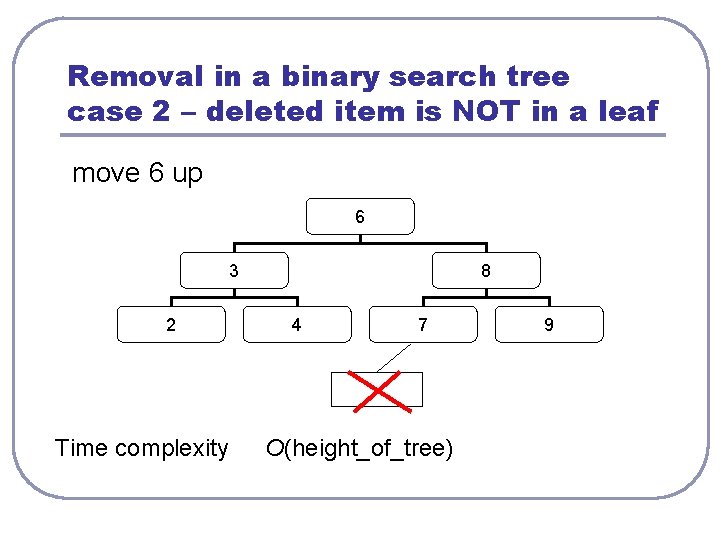
Removal in a binary search tree case 2 – deleted item is NOT in a leaf move 6 up 6 3 2 Time complexity 8 4 7 O(height_of_tree) 9

Removal in a binary search tree delete. Item(s, t) { x = search. Item(s, t) if(x == null) return // nothing to remove if(x is a leaf) remove node x else if(x. right != null) y = find. Leftmost(x. right) else if(x. left != null) y = find. Rightmost(x. left) move value in y to x, then remove node y }