Basic Data Structures in Prolog Lists and Graphs

Overview Lists List Operations Graph Operations

Lists What are the classic properties of lists? n n Easy to insert and delete at end (free pointer) Harder to change in the middle O(n) to search unless ordered Variable size

Prolog Lists The major complex data structure Can contain atoms, variables, etc. Have 2 parts, a Head and a Tail n n n Head is the first element in a list Tail is everything else [Head|Tail] The empty list [] is a list Every list has an empty list at the end

Getting a Feel for Lists head( [H|T], H ). tail( [H|T], T ). Every nontrivial list operation involves recursion

Member member( H, [H|T] ). member( H, [_|T] ): member( H, T ).

Append append( H, [], [H] ). append( X, [H|T], [H|T 2] ): append( X, T, T 2 ).

Delete delete( H, [H|T], T ). delete( X, [H|T], [H|T 2] ): delete( X, T, T 2 ). Delete can test membership!

Length length( [], 0 ). length( [H|T], X+1 ): length( T, X ).

Concat concat( H, [], H ). concat( [H|T], [H 2|T 2], [H|T 3] ): append( H 2, T, H 3 ), concat( H 3, T 2, T 3 ). concat 2( [], H, H ). concat 2( [H|T], L 2, [H|T 2] ): concat 2( T, L 2, T 2 ).

Sort sort 1( [], [] ). sort 1( L 1, L 2 ): permute( L 1, L 2 ), ordered( L 2 ).

Permute permute( [], [] ). permute( L, [H|T] ): delete( H, L, L 2 ), permute( L 2, T ).

Ordered ordered( [] ). ordered( [X|[]] ). ordered( [H|[H 2|T]] ): H < H 2, ordered( [H 2|T] ).

Flatten - Double Recursion flatten( [], [] ). flatten( X, [X] ): atomic( X ), X == []. flatten( [H|T], L ): flatten( H, H 2 ), flatten( T, T 2 ), concat( H 2, T 2, L ).

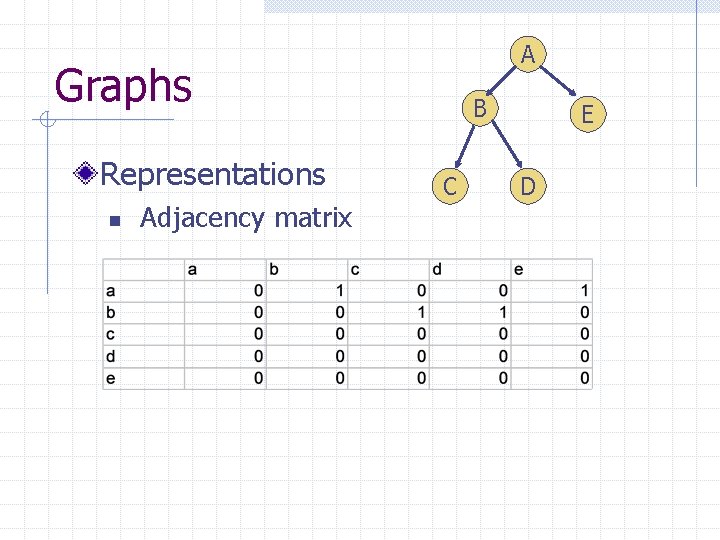
A Graphs Representations n Adjacency matrix B C E D

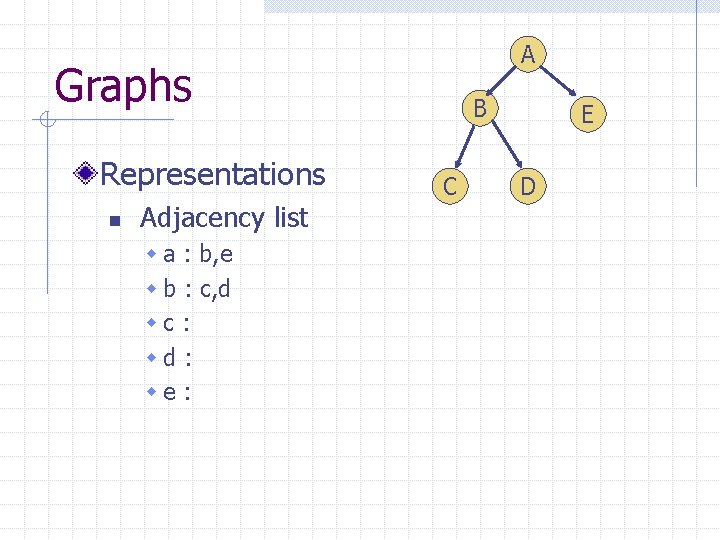
A Graphs Representations n Adjacency list w a : b, e w b : c, d wc : wd : we : B C E D

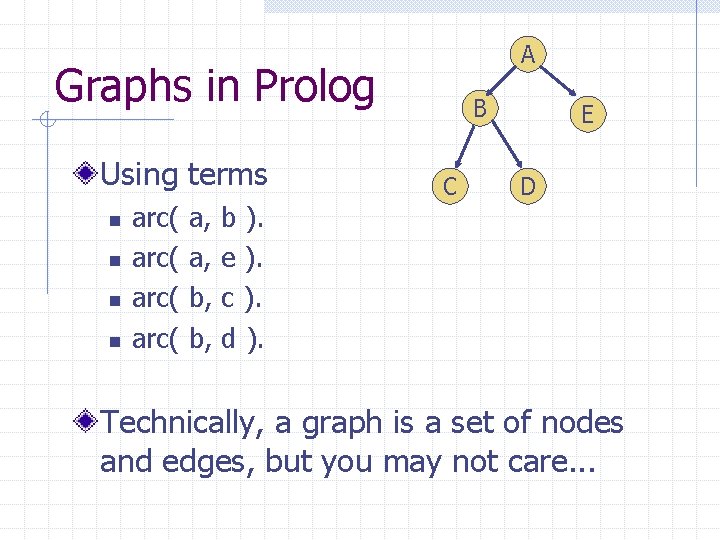
A Graphs in Prolog Using terms n n arc( a, b ). a, e ). b, c ). b, d ). B C E D Technically, a graph is a set of nodes and edges, but you may not care. . .

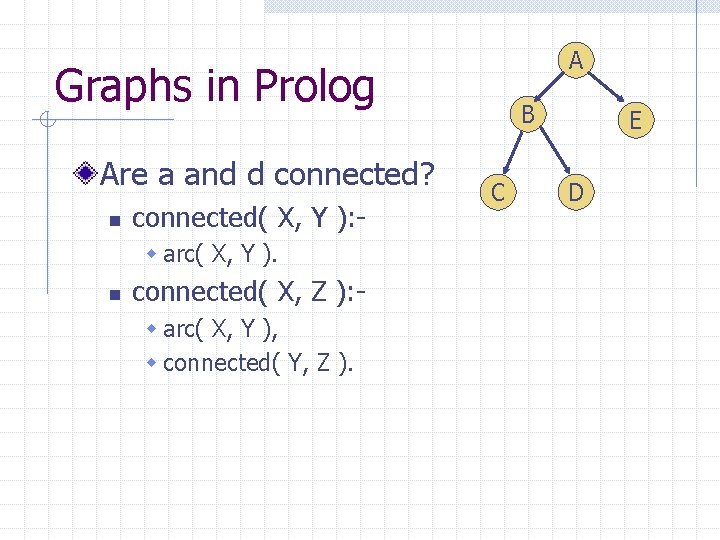
A Graphs in Prolog Are a and d connected? n connected( X, Y ): w arc( X, Y ). n connected( X, Z ): w arc( X, Y ), w connected( Y, Z ). B C E D

A Depth First Search Return path to goal state n dfs( N, [] ): w goal( N ). n dfs( N, [H|T] ): w connected( N, H ), w dfs( H, T ). B C E D

Graphs in Prolog What if you want a graph/tree to be an argument to a predicate? graph([nodes], [edges]) n graph([a, b, c, d, e], [arc(a, b), arc(a, e), arc(b, c), arc(b, d)] graph( t(node, [edgenodes]), . . . ) n graph( t(a, [b, e]), t(b, [c, d]), t(c, []), t(d, []), t(e, []) )