BASIC CRYPTOGRAPHIC CONCEPTS Public Key Cryptography Uses two

BASIC CRYPTOGRAPHIC CONCEPTS

Public Key Cryptography Uses two keys for every simplex logical communication link. � Public key � Private key The use of two keys has profound consequences in the areas of � Confidentiality � Key distribution � Authentication

Basic ingredients of the scheme: � Plaintext Message to be encrypted � Public (P) Key (KU) and Private Key (KR) One with the sender and other with the receiver � Ciphertext Message after encryption � Encryption algorithm (EA) Uses P and KU � Decryption (C) algorithm (DA) Uses C and KR

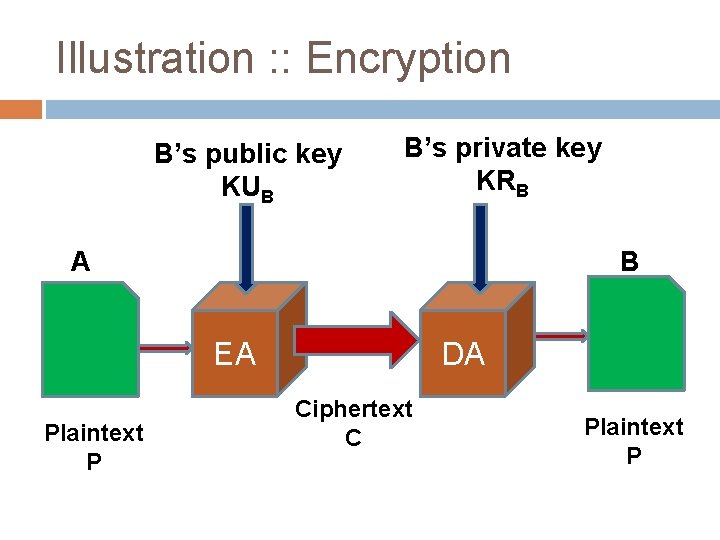
Illustration : : Encryption B’s public key KUB B’s private key KRB A B EA Plaintext P DA Ciphertext C Plaintext P

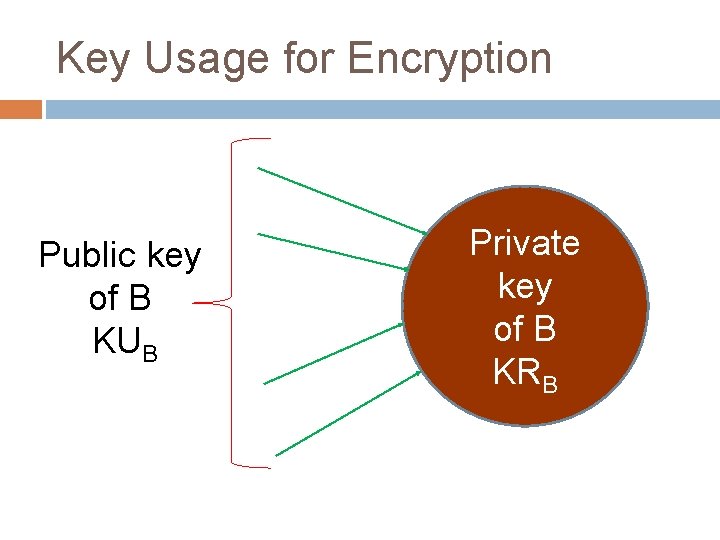
Key Usage for Encryption Public key of B KUB Private key of B KRB

Illustration : : Authentication A’s private key KRA A’s public key KUA A B EA Plaintext P DA Ciphertext C Plaintext P

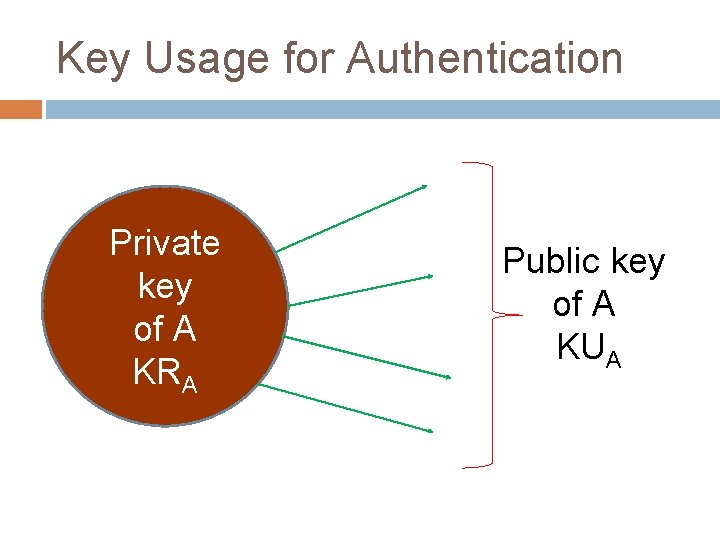
Key Usage for Authentication Private key of A KRA Public key of A KUA

Applications Three categories: � Encryption/decryption: The sender encrypts a message with the recipient’s public key. � Digital The � Key signature / authentication: sender signs a message with its private key. exchange: Two sides cooperate to exchange a session key.

Requirements Computationally easy for a party B to generate a key pair � Public key KUB � Private key KRB Easy for sender to generate ciphertext C = E (M, KUB ) Easy for receiver to decrypt ciphertext using private key: M = D(C, KRB ) = D(E (M, KUB ), KRB )

Computationally infeasible to determine KRB knowing KUB. Computationally infeasible to recover message M, knowing KUB and ciphertext C. Either of the two keys can be used for encryption, with the other used for decryption: M = D (E (M, KUB ), KRB)= D ( E (M, KRB), KUB)

The RSA Public Key Algorithm RSA Algorithm � Developed by Ron Rivest, Adi Shamir and Len Adleman at MIT, in 1977. � A block cipher. Not � The fixed size most widely implemented.

RSA : Key Generation 1. 2. 3. 4. 5. 6. 7. Select p, q p and q both prime Calculate n = p × q Calculate ɸ(n) = (p-1)(q-1) Select integer e gcd(ɸ(n), e) =1 ; 1<e< ɸ(n) Calculate d de=1 mod ɸ(n) Public Key KU={e, n} Private Key KR={d, n} ɸ(n) is the number of positive number less than n and relatively prime to n (called Euler totient).

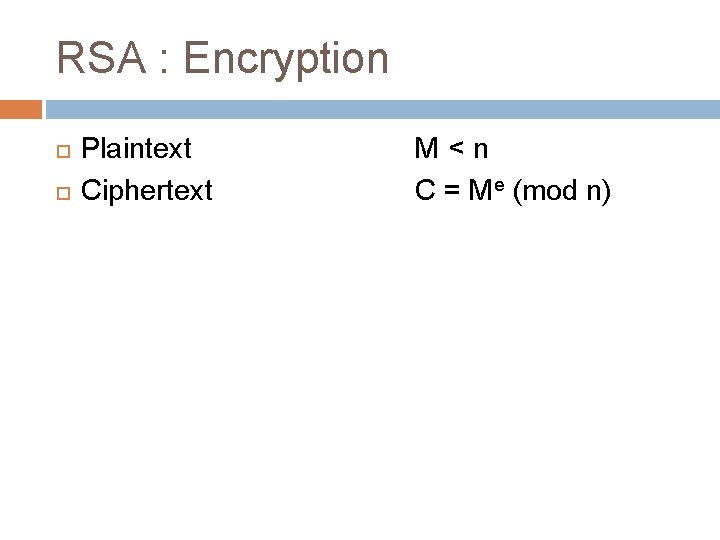
RSA : Encryption Plaintext Ciphertext M<n C = Me (mod n)

RSA : Decryption Ciphertext Pliantext C M= Cd (mod n)

Example Select two prime numbers, p=7 and q=17. Calculate n=pq= 7× 17 = 119. Calculate ɸ(n) = (p-1)(q-1) =96. Select e such that e is relatively prime to ɸ(n)=96, and less than ɸ(n). � In this case, e=5. Determine d such that de = 1 mod 96 and d<96. � D=77, because 77 × 5 = 385 = 4 × 96 + 1. Public key KU = {5, 119} Private key KR={77, 119}

Encryption process: � Say, plaintext M = 19. � Ciphertext C= 195 mod 119 = 2476099 mod 119 = 66 Decryption process: �M = 6677 mod 119 = 19.

The security of RSA is secure since � We use large number of bits in e and d. � The problem of factoring n into two prime factors is computationally very difficult. Knowing p and q will allow us to know ɸ(n). This will help an intruder to know the values of e and d. � Key safe sizes in the range of 1024 to 2048 bits seems

Until recently, this was felt to be infeasible for numbers in the range of 100 decimal digits or so (approximately 300 bit). A worldwide team cooperating over the internet and using 1600 computers recently cracked the code in eight months. Currently, a 1024 -bit key size (about 300 decimal digits) is considered strong enough for virtually all applications.

Diffie-Hellman Key Exchange Proposed in 1976. Allows group of users to agree on secret key over insecure channel. Cannot be used to encrypt and decrypt messages. Depends for its effectiveness on the difficulty of computing discrete logarithms.

D-H Algorithm A and B want to agree on secret key. � They agree on two large numbers n and g, such that 1<g<n. � A choose random x, computes X=gx mod n, and sends X to B. � B chooses random y, computes Y=gy mod n, and sends Y to A. � A computes k 1 =Yx mod n. � B computes k 2 =Xy mod n. Note: k 1 =k 2 = gxy mod n.

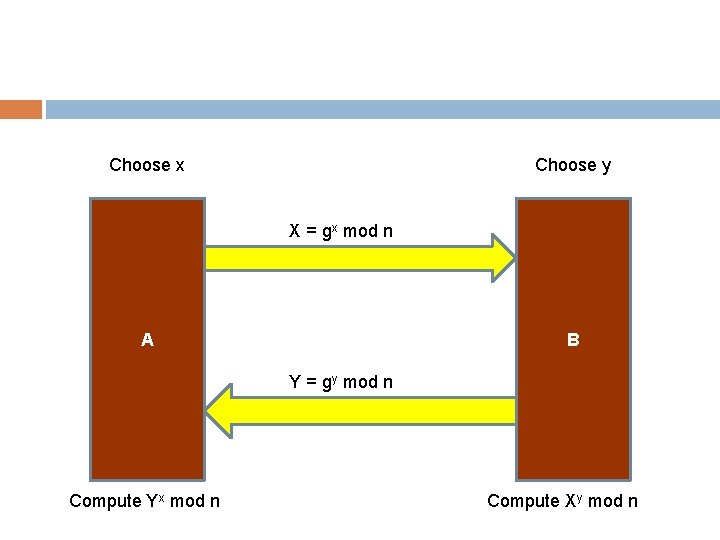
Choose x Choose y X = gx mod n A B Y = gy mod n Compute Yx mod n Compute Xy mod n

D-H Algorithm Requires no prior communication between A and B. Security depends on difficulty of computing x, given X = gx mod n. Choices for g and n are critical. � Both n and (n-1)/2 should be prime. � n should be large. Susceptible to intruder-in-the-middle (man-inthe-middle) attack. � Active intruder.

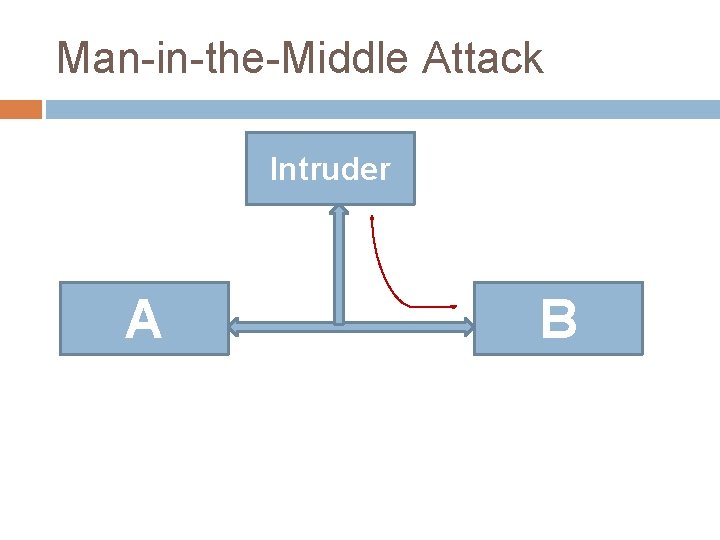
Man-in-the-Middle Attack Intruder A B

A Comparison Symmetric encryption/decryption is much faster than asymmetric encryption/decryption: RSA: kilobits/second DES: megabits/second DES is about 100 times faster than RSA Key size: � RSA: selected by user � DES: 56 bits

Message Authentication

Various Approaches Authentication using conventional encryption. � Only the sender and receiver should share a key. Message authentication without message encryption. An authentication tag is generated and appended to each message. Message authentication code. Calculate the MAC as a function of the message and key: MAC = F(K, M)

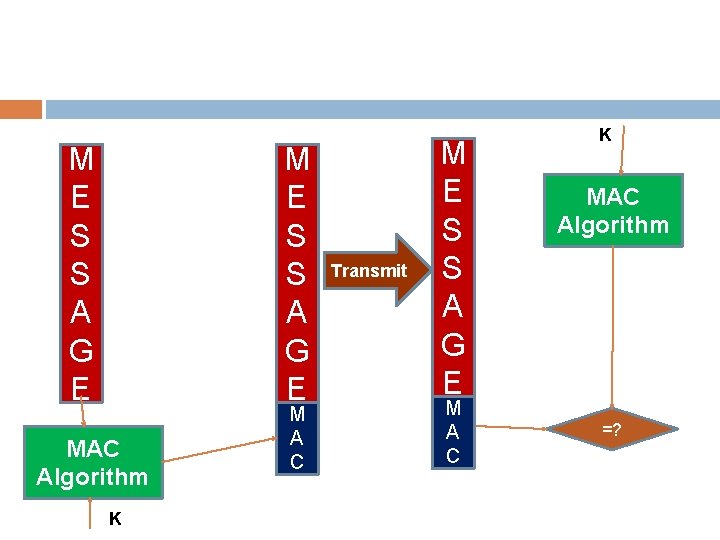
M E S S A G E MAC Algorithm K M A C Transmit M E S S A G E M A C K MAC Algorithm =?

Commonly Used Schemes The MD family � MD 2, MD 4 and MD 5 (128 -bit hash). The SHA family � SHA-1 (160 -bit), SHA-256 (256 -bit), SHA-384 (384 -bit) and SHA-512 (512 -bit). RIPEMD-128 (128 -bit), RIPEMD-160 (160 -bit).