Basic Concepts of Thermodynamics Dept Phys Tunghai Univ

Basic Concepts of Thermodynamics Dept. Phys. , Tunghai Univ. Biophysics, C. T. Shih

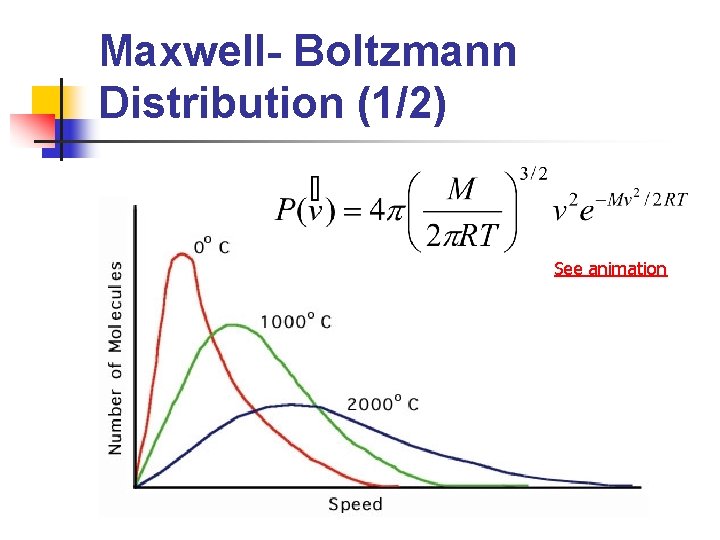
Maxwell- Boltzmann Distribution (1/2) See animation

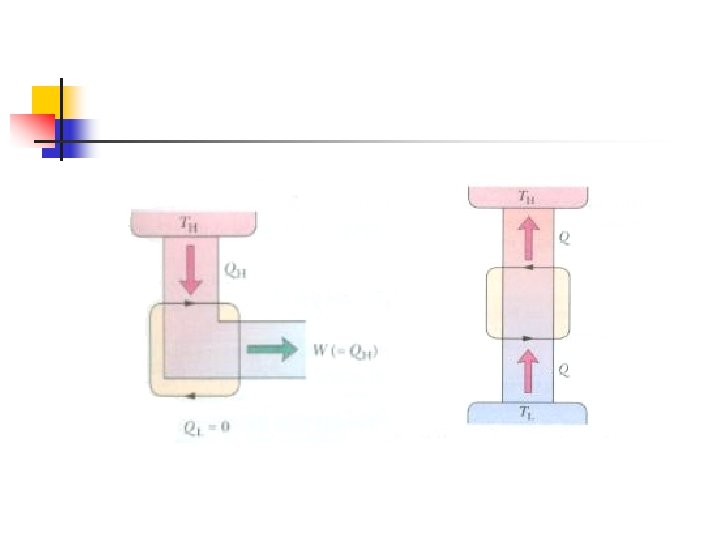
Second Law of Thermodynamics n n n Kelvin-Planck statement: 淨反應為由一熱 庫（heat reservior）抽出熱能Q完全轉換為 功W的熱機（heat engine）不存在 Clausius statement: 淨反應為將熱能由低溫 熱庫抽至高溫熱庫的熱機不存在 These two statements are equivalent!

Entropy and Probability (2/2) n n 每個微觀狀態出現的機率均等 平衡態即是W最大的分佈狀態，滿足Maxwell. Boltzmann distribution 複合系統之entropy可加成 S=S 1+S 2 此時的entropy滿足Boltzmann’s entropy equation: S=kln. W

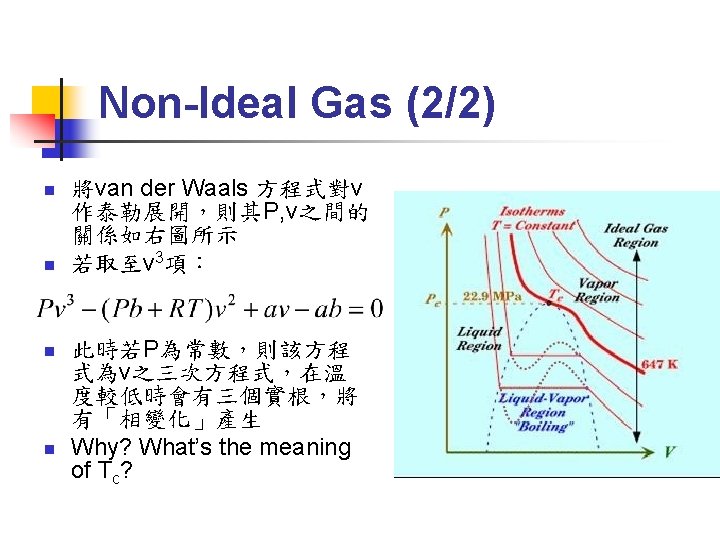
Thermal Equilibrium (1/4) Fundamental equation：系統內能為S, V, N等 external parameters（與系統大小成正比的量） 的函數，可寫為：U=U(S, V, N 1, N 2, N 3……） n 也可寫為：S=S(U, V, N 1, N 2, N 3……） n 練習：導出理想氣體的 fundamental equation 為： n

Thermal Equilibrium (2/4) n 取 fundamental equation 之微分： n 可以定義出一組與系統大小無關的量： 稱為 intensive parameters

Extremum Principle (1/2) n n n Entropy minimum principle: The equilibrium value of any unconstrained internal parameter is such as to maximize the entropy for the given value of the total energy. Energy minimum principle: The equilibrium value of any unconstrained internal parameter is such as to minimize the energy for the given value of total entropy. These two principles are equivalent!

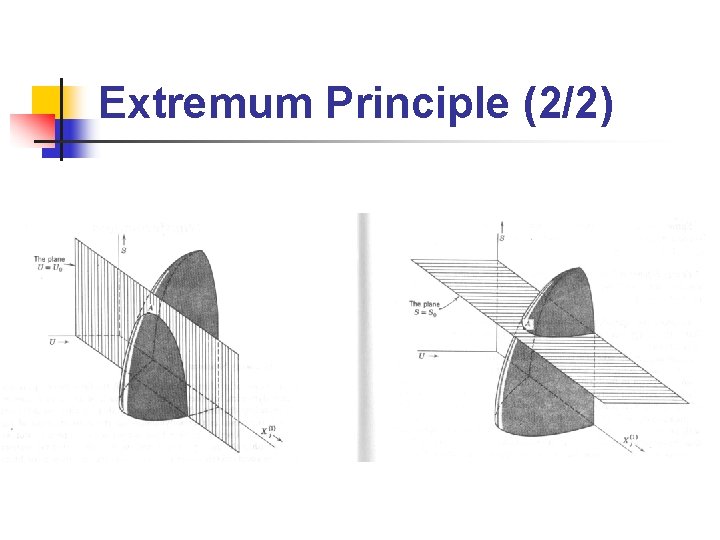
Extremum Principle (2/2)

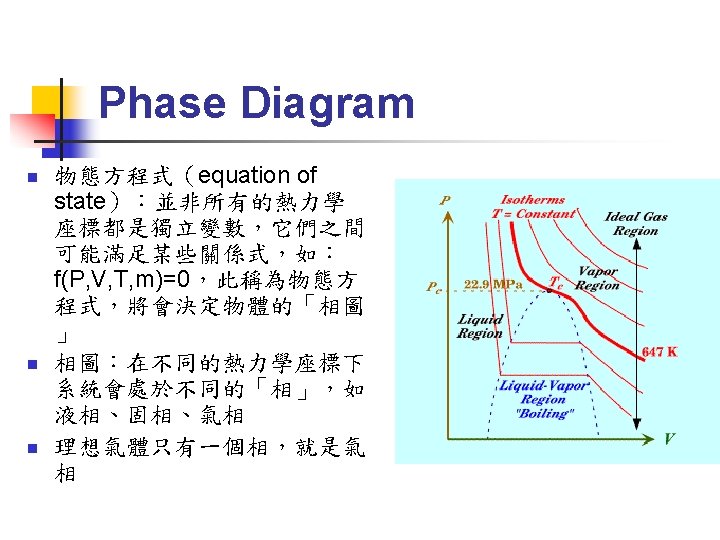
Legendre Transformations n n Fundamental equation: U=U(S, V, N)，是 以extensive paramters（S, V, N）為座標 欲找一等價的方程式，但以前述 intensive parameters（P, T, m）為座標 Why? 實驗上，（P, T, m）較（S, V, N）易 於測量與控制 Legendre transformation即為此 extensive/intensive 變數變換的方法

Helmholtz Free Energy

Enthalpy

Gibbs Free Energy

Grand Canonical Potential

Now the Extremum Principles become… n n Hemholtz free energy is minimized at constant temperature Enthalpy is minimized at constant pressure Gibbs function is minimized at constant temperature and constant pressure All these principles are equivalent!

Stability of Thermodynamic Systems (2/3) n 由d. U=0與d 2 U＞ 0可推出，平衡態下的任 一子系統必須滿足以下條件（u=U/N， f=F/N，v=V/N，uss=d 2 u/ds 2）：

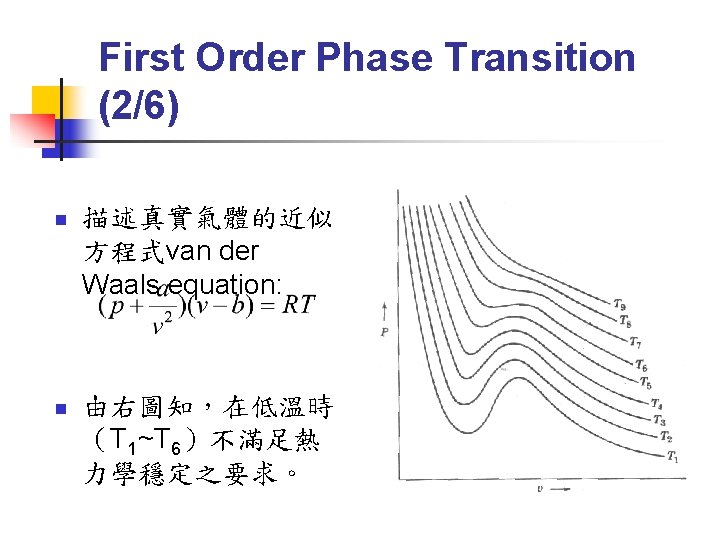
First Order Phase Transition (3/6) n Gibbs-Duhem Relation: n Φ(T) 只與溫度有關，因此在等溫過程中：

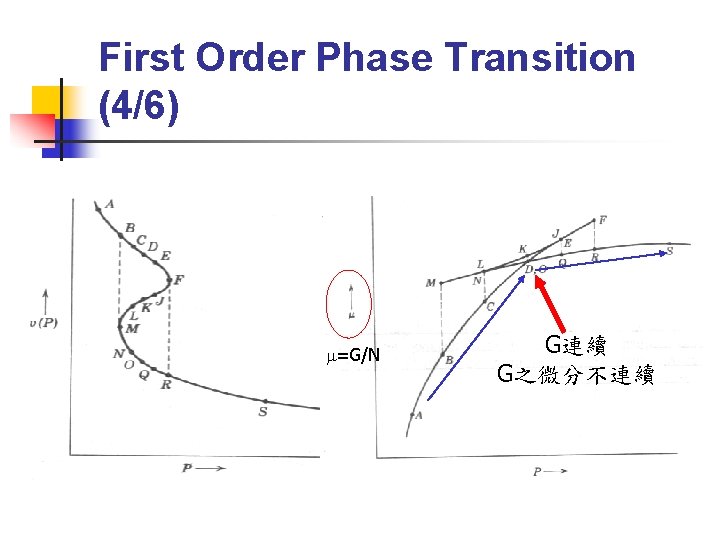
First Order Phase Transition (4/6) m=G/N G連續 G之微分不連續

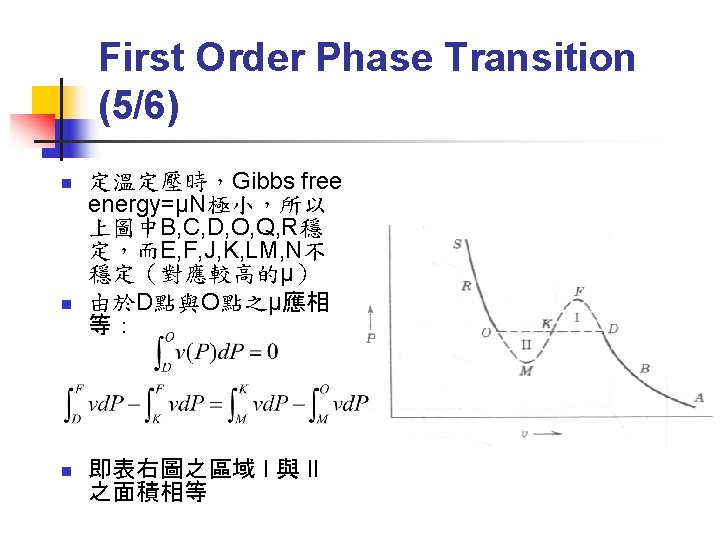
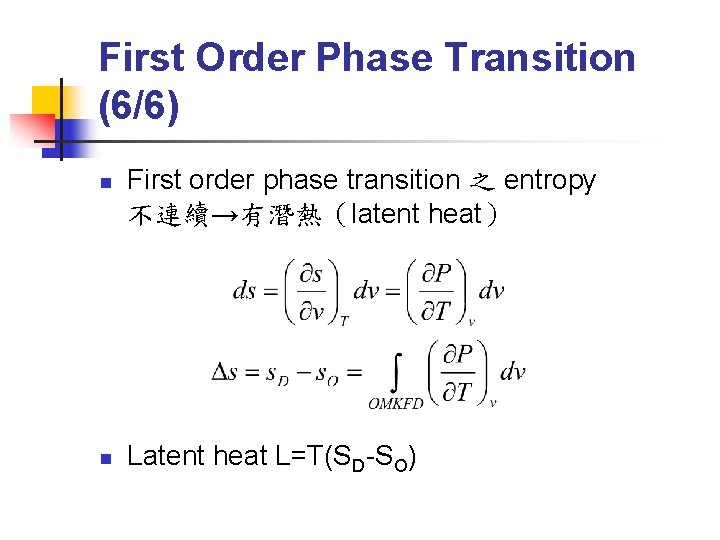
First Order Phase Transition (6/6) n n First order phase transition 之 entropy 不連續→有潛熱（latent heat） Latent heat L=T(SD-SO)

Summary of Part. 2 n n Fundamental equation of thermodynamics Detailed description of equilibrium Extremum principle and different thermodynamic potential Stability of equilibrium and phase transition

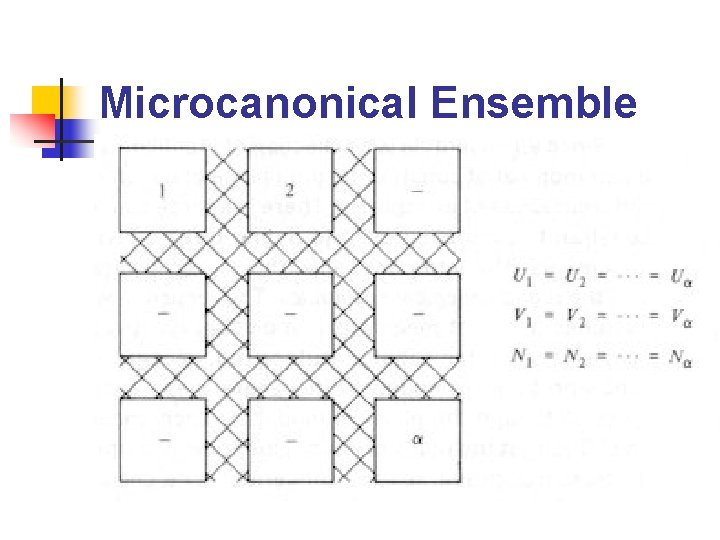
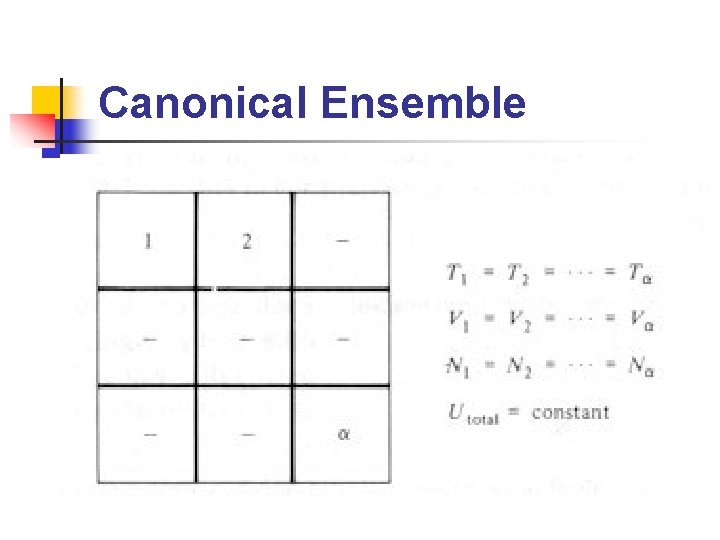
Ensembles (2/2) n n Microcanonical ensemble: ensemble 中所有系 統的N, V, U相等 Canonical ensemble: ensemble 中所有系統之 N, V, T 相等 Grand canonical ensemble: ensemble 中所有 系統之μ, V, T 相等 在不同的條件下（constant temperature, constant pressure……etc. ）使用不同的 ensemble 會比較方便

Microcanonical Ensemble

Canonical Ensemble

Grand Canonical Ensemble

Canonical Ensemble (3/3) n n 對W(a)求極大值，即得Maxwell-Boltzmann distribution Q稱為「partition function」，各物理量滿足：

Grand Canonical Ensemble

Quantum Statistics (2/3) n 對費米子而言，由於有 Pauli’s exclusion principle，nk只能為 0或 1，因此 partition function 為： n 因此可求出，佔據 k 態的粒子數期望值為： n 此稱為 Fermi-Dirac distribution

Quantum Statistics (3/3) n Boson system: 沒有 exclusion principle，所 以 nk 可以是 0, 1, 2…∞，因此其 partition function 為： n 同理，佔據 k 態的粒子數期望值為： n 此稱為 Bose-Einstein distribution

Summary of Part. 3 n n Ensembles and ensemble average Partition functions of ensembles Thermodynamic variables and the partition function Quantum statistics