Basic Concepts of Computers Most computer systems consists

Basic Concepts of Computers

Most computer systems consists of three basic structures or subsystems: § The high speed memory unit also called Random Access Memory (RAM). § The Central Processing Unit (CPU). The CPU is the brains of the computer. § The I/O subsystem (Communicating with Input and Output devices). 2

Number Systems and Codes The most commonly used numbering system is the decimal system. However, due to the binary nature of electronic devices, the use of decimal system by the computer is limited. Most of the data representation and arithmetic operations are carried out in the binary system or some of its “shorthand” notation such as the octal or hexadecimal systems. 3

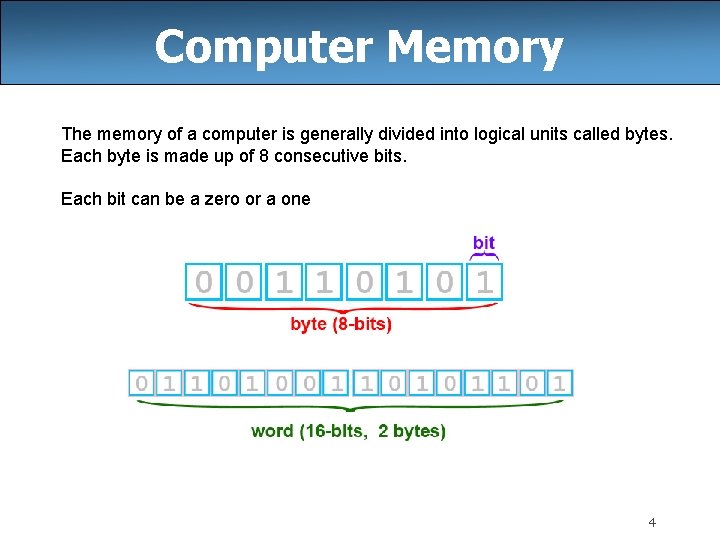
Computer Memory The memory of a computer is generally divided into logical units called bytes. Each byte is made up of 8 consecutive bits. Each bit can be a zero or a one 4

Address Space • The Address space is the set of all unique addresses that a program can reference. The size of this space can be calculated by where n is the number of bits Used to represent the address. • Bytes are also grouped into larger units. 1 nibble 4 consecutive bits 1 byte 8 consecutive bits 1 word 2 consecutive bytes 1 longword 4 consecutive bytes 1 quadword 8 consecutive bytes 1 octaword 16 consecutive bytes 5

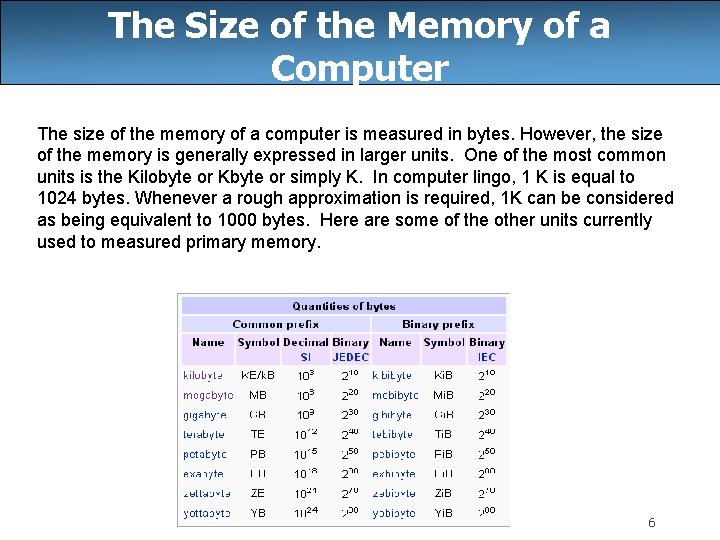
The Size of the Memory of a Computer The size of the memory of a computer is measured in bytes. However, the size of the memory is generally expressed in larger units. One of the most common units is the Kilobyte or Kbyte or simply K. In computer lingo, 1 K is equal to 1024 bytes. Whenever a rough approximation is required, 1 K can be considered as being equivalent to 1000 bytes. Here are some of the other units currently used to measured primary memory. 6

Converting binary Numbers to Decimal Numbers Convert 1 1 0 01 1 0 1 to decimal = 205 7

Converting binary Numbers to Decimal Numbers • Convert to Decimal 11001 = 25 1000111 =71 10101 =341 8

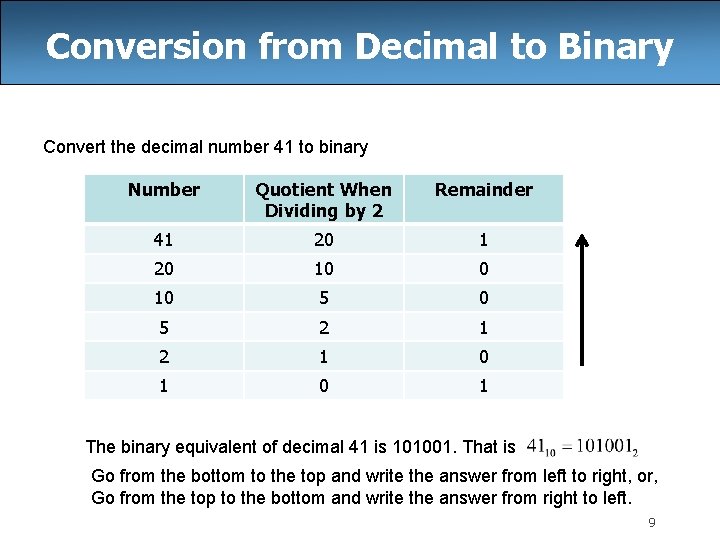
Conversion from Decimal to Binary Convert the decimal number 41 to binary Number Quotient When Dividing by 2 Remainder 41 20 10 5 2 1 0 1 The binary equivalent of decimal 41 is 101001. That is Go from the bottom to the top and write the answer from left to right, or, Go from the top to the bottom and write the answer from right to left. 9

Conversion from Decimal to Binary Convert the following Decimal Number to a Binary Number 92 =1011100 300 =100101100 10

Hexadecimal Number System 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 What is the decimal equivalent of the hexadecimal number 1 A 5 F 11

Hexadecimal Number System What is the binary equivalent of the hexadecimal number AF 3 B 1 A F 3 B 1 1010 1111 0011 1011 0001 = 10101111001110110001 12

Hexadecimal Number System What is the decimal equivalent of the following hexadecimal number? EF 5 A =61274 What is the binary equivalent of the following hexadecimal number? 39 A =1110011010 13

Hexadecimal Number System What is the hexadecimal equivalent of the binary number 011001111010100111 01 1001 1110 1010 0111 = 19 EAA 7 What is the hexadecimal equivalent of the binary number 1010111100011 =15 E 3 14

Hexadecimal Number System What is the hexadecimal representation of decimal 300 Number Quotient When Dividing by 16 Remainder 300 18 12 18 1 2 1 0 1 Therefore 300 in decimal is 12 C in the hexadecimal number system What is the hexadecimal representation of decimal 425 =1 A 9 15

Octal Number System • Octal Numeral System - Base-8 • Octal numbers uses digits from 0. . 7. • Examples: Convert the octal number into a decimal • 278 = 2× 81+7× 80 = 16+7 = 23 • 308 = 3× 81+0× 80 = 24 • 43078 = 4× 83+3× 82+0× 81+7× 80= 2247 16

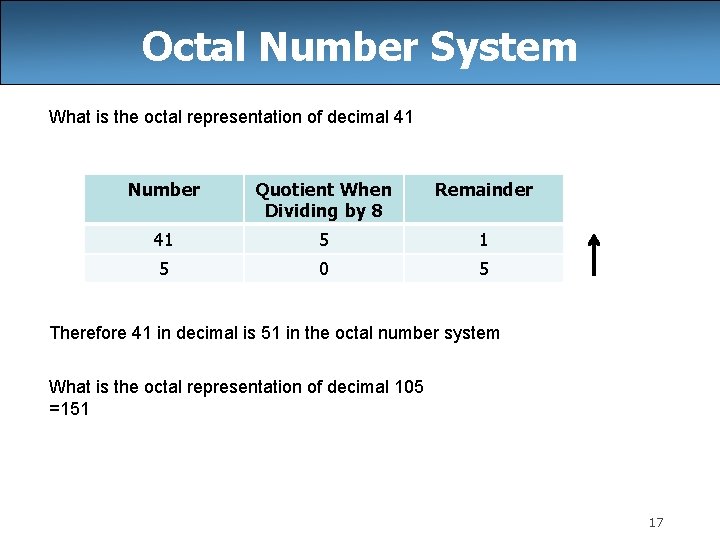
Octal Number System What is the octal representation of decimal 41 Number Quotient When Dividing by 8 Remainder 41 5 0 5 Therefore 41 in decimal is 51 in the octal number system What is the octal representation of decimal 105 =151 17