Basic Communication Operations Carl Tropper Department of Computer

Basic Communication Operations Carl Tropper Department of Computer Science

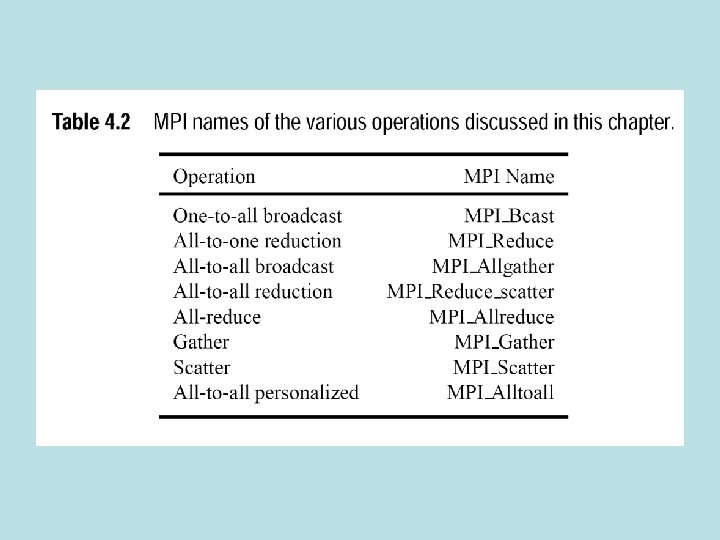
Building Blocks in Parallel Programs • Common interactions between processes in parallel programs-broadcast, reduction, prefix sum…. • Study their behavior on standard networksmesh, hypercube, linear arrays • Derive expressions for time complexity – Assumptions are: send/receive one message on a link at a time, can send on one link while receiving on another link, cut through routing, bidirectional links – Message transfer time on a link: ts + twm

Broadcast and Reduction • One to all broadcast • All to one reduction • p processes have m words apiece • associative operation on each wordsum, product, max, min • Both used in • Gaussian elimination • Shortest paths • Inner product of vectors

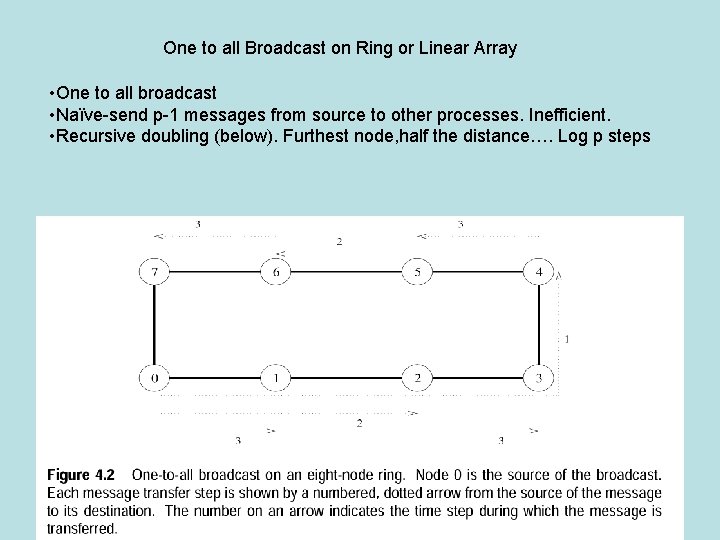
One to all Broadcast on Ring or Linear Array • One to all broadcast • Naïve-send p-1 messages from source to other processes. Inefficient. • Recursive doubling (below). Furthest node, half the distance…. Log p steps

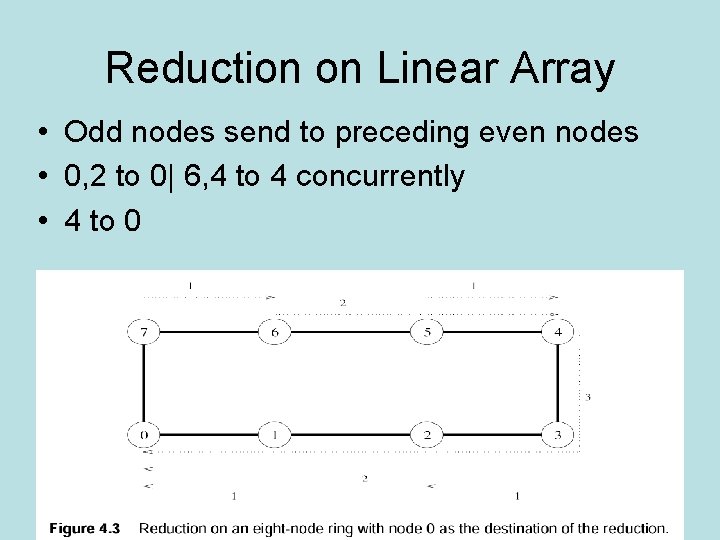
Reduction on Linear Array • Odd nodes send to preceding even nodes • 0, 2 to 0| 6, 4 to 4 concurrently • 4 to 0

Matrix vector multiplication on an nxn mesh • Broadcast input vector to each row • Each row does reduction

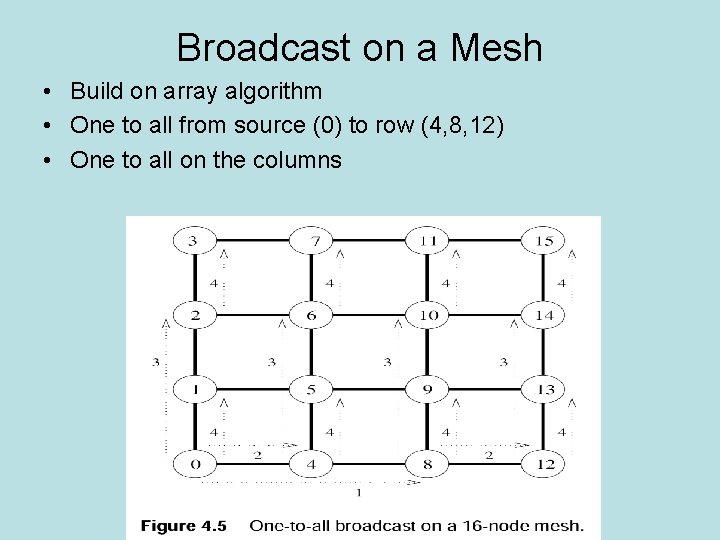
Broadcast on a Mesh • Build on array algorithm • One to all from source (0) to row (4, 8, 12) • One to all on the columns

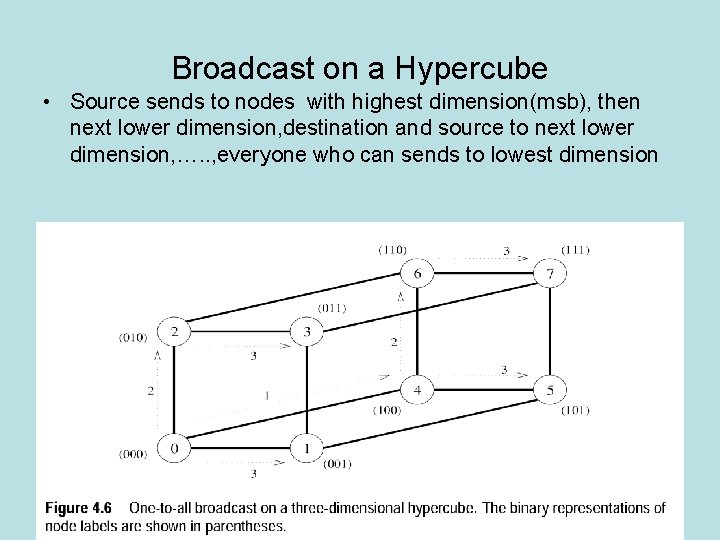
Broadcast on a Hypercube • Source sends to nodes with highest dimension(msb), then next lower dimension, destination and source to next lower dimension, …. . , everyone who can sends to lowest dimension

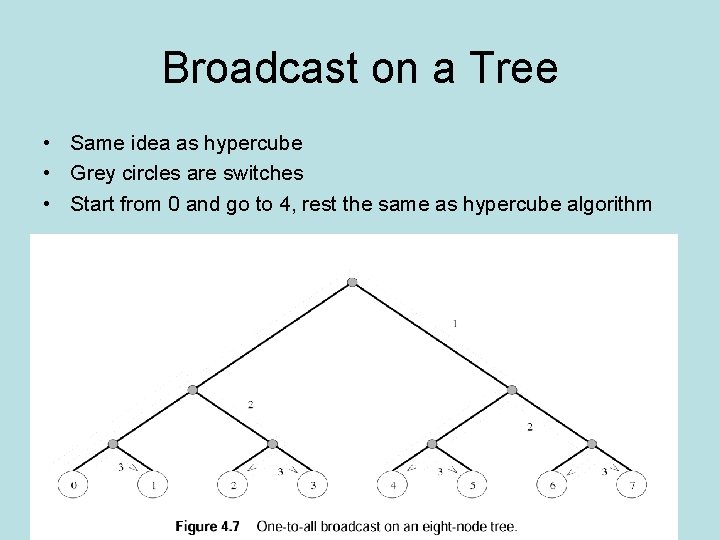
Broadcast on a Tree • Same idea as hypercube • Grey circles are switches • Start from 0 and go to 4, rest the same as hypercube algorithm

All to all broadcast on linear array/ring • Idea-each node is kept busy in a circular transfer

All to all broadcast on ring

All to all broadcast • Mesh-each row does all to all. Nodes do all to all broadcast in their columns. • Hypercube-pairs of nodes exchange messages in each dimension. Requires log p steps.

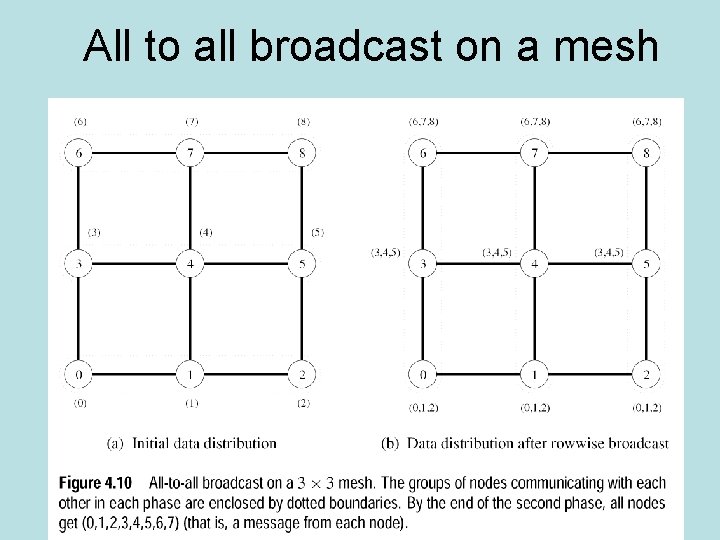
All to all broadcast on a mesh

All to all broadcast on a hypercube • Hypercube of dimension p is composed of two hypercubes of dimension p-1 • Start with dimension one hypercubes. Adjacent nodes exchange messages • Adjacent nodes in dimension two hypercubes exchange messages • In general, adjacent nodes in next higher dimensional hypercubes exchange messages • Requires log p steps.

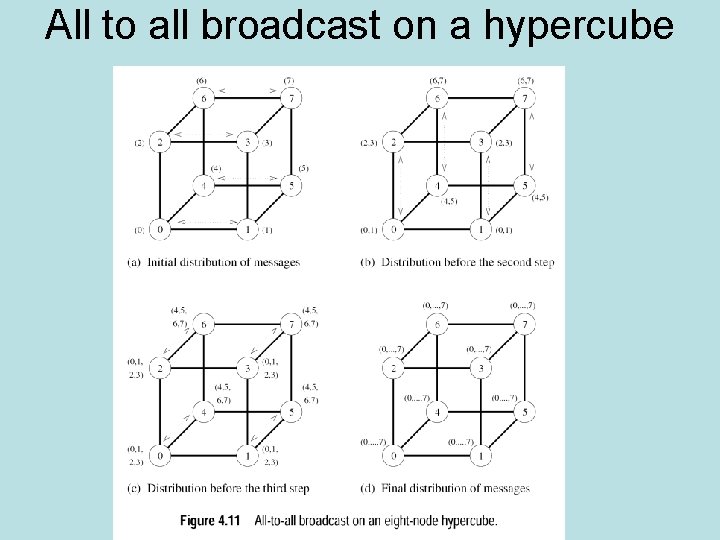
All to all broadcast on a hypercube

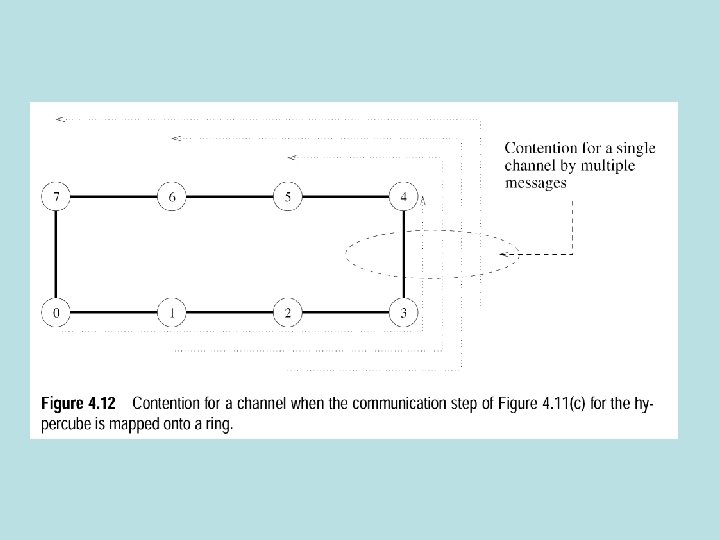
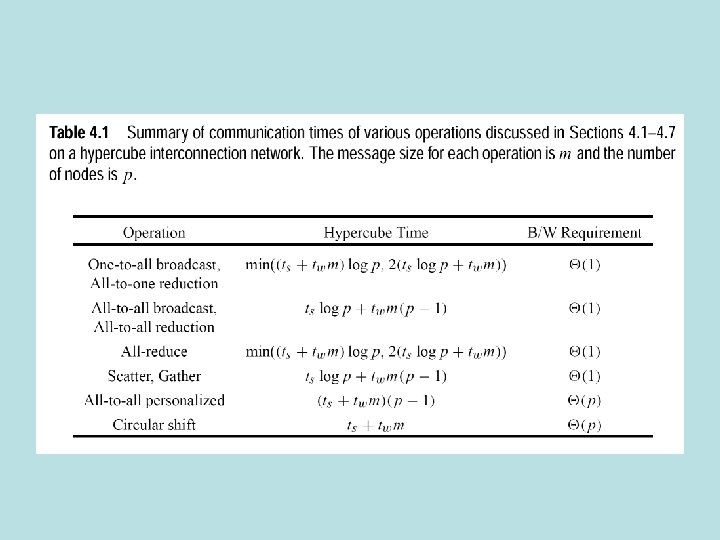
All to all broadcast time • Ring or Linear Array T=(ts+twm)(p-1) • Mesh • 1 st phase: √p simultaneous all to all broadcasts among √p nodes takes time (ts+ twm)(√p-1) • 2 nd phase: size of each message is m√p, phase takes time (ts+twm√p) )(√p-1) • T=2 ts(√p-1)+twm(p-1) is total time • Hypercube • Size of message in ith step is 2 i-1 m • Takes ts+2 i-1 twm for a pair of nodes to send and receive messages • T=∑I=1 logp (ts+2 i-1 twm)=tslog p + twm(p-1)

Observation on all to all broadcast time • Send time neglecting start up is the same for all 3 architectures: twm(p-1) • Lower bound on communication time for all 3 architectures

All Reduce Operation • All reduce operation-all nodes start with buffer of size m. Associative operation performed on all buffers-all nodes get same result. • Semantically equivalent to all to one reduction followed by one to all broadcast. • All reduce with one word implements barrier synch for message passing machines. No node can finish reduction before all nodes have contributed to the reduction. • Implement all reduce using all to all broadcast. Add message contents instead of concatenating messages. • In hypercube, T=(ts+twm)log p for log p steps because message size does not double in each dimension.

Prefix Sum Operation • Prefix sums (scans) are all partial sums, sk, of p numbers, n 1, …. , np-1, one number living on each node. • Node k starts out with nk and winds up with sk • Modify all to all broadcast. Each node only uses partial sums from nodes with smaller labels.

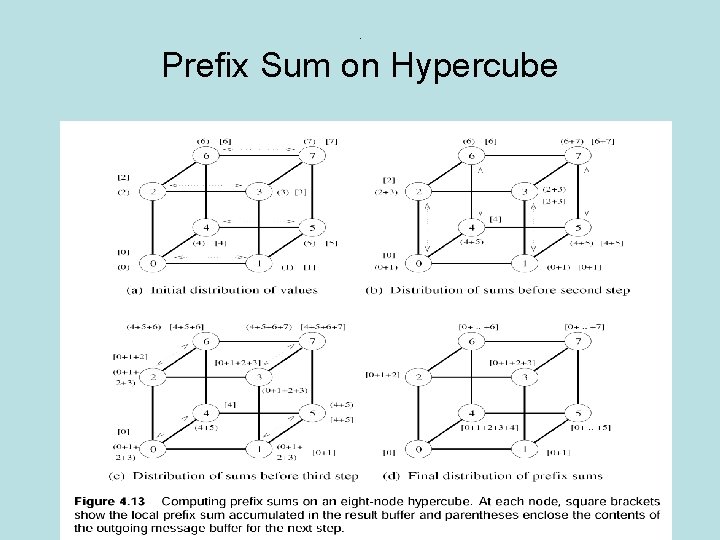
. Prefix Sum on Hypercube

Prefix sum on hypercube

Scatter and gather • Scatter (one to all personalized communication) source sends unique message to each destination (vs broadcast - same message for each destination) – Hypercube: use one to all broadcast. Node transfers half of its messages to one neighbor and half to other neighbor at each step. Data goes from one subcube to another. Log p steps. • Gather: Node collects unique messages from other nodes – Hypercube: Odd numbered nodes send buffers to even nodes in other (lower dimensional) cube. Continue….

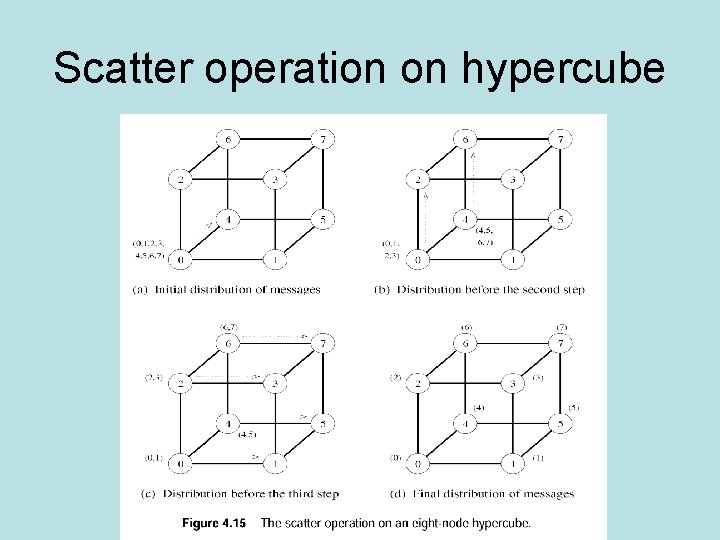
Scatter operation on hypercube

All to all personalized communication • Each node sends distinct messages to every other node. • Used in FFT, Matrix transpose, sample sort • Transpose of A[i, j] is AT=A[j, i] , 0≤ i, j ≤ n • Put row i {(i, o), (i, 1), …. , (i, n-1) } processor Pi • Transpose-(i, 0) goes to P 0, (i, 1) goes to processor 1, (i, n) goes to Pn • Every processor sends a distinct element to every other processor! • All to all on ring, mesh, hypercube

All to all on ring, mesh, hypercube • Ring: All nodes send messages in same direction. • Each node sends p-1 message of size m to neighbor. • Nodes extract message(s) for them, forward rest • Mesh: p x p mesh. Each node groups destination nodes into columns • All to all personalized communication on each row • Upon arrival, messages are sorted by row • All to all communication on rows • Hypercube p node hypercube – p/2 links in same dimension connect 2 subcubes with p/2 nodes • Each node exchanges p/2 messages in a given dimension

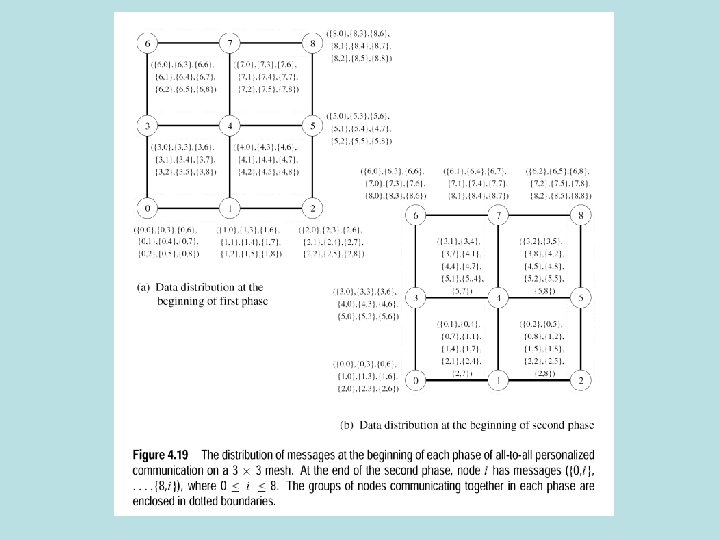
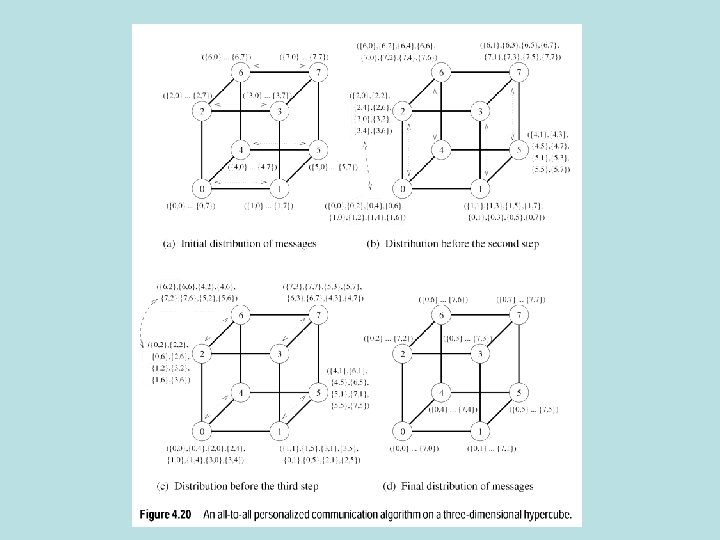
All to all personalized communication -optimal algorithm on a hypercube • Nodes chose partners for exchange in order to not suffer congestion • In step j node i exchanges with node i XOR j • First step-all nodes differing in lsb exchange messages…………. . • Last step-all nodes differing msb exchange messages • E cube routing in hypercube implements this • (Hamming) distance between nodes is # non-zero bits in i xor j • Sort links corresponding to non-zero bits in ascending order • Route messages along these links

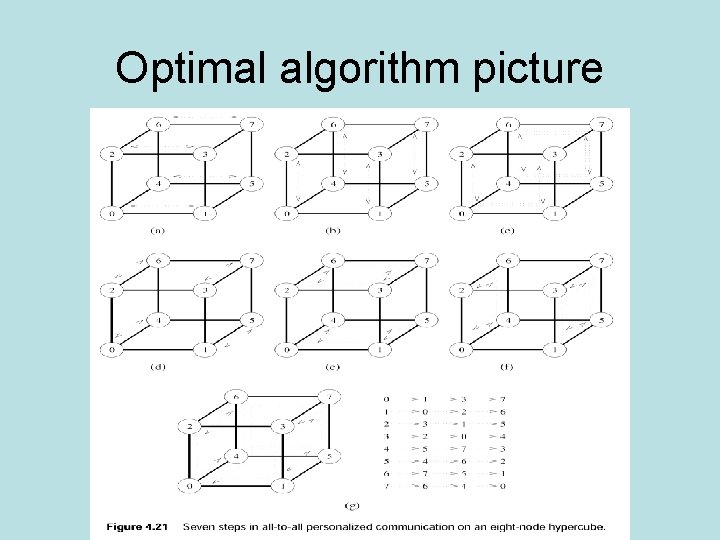
Optimal algorithm picture

Optimal algorithm • T=(ts+twm)(p-1)

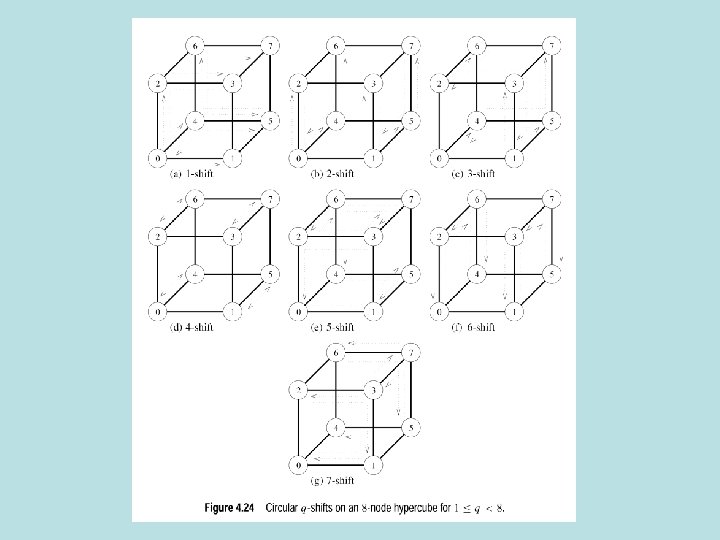
Circular q Shift • Node i sends packet to (i+q) mod p • Useful in string, image pattern matching, matrix comp… • 5 shift on 4 x 4 mesh • Everyone goes 1 to the right (q mod √p) • Everyone goes 1 upwards q/√p • Left column goes up before general upshift to make up for wraparound effect in first step

Mesh Circular Shift

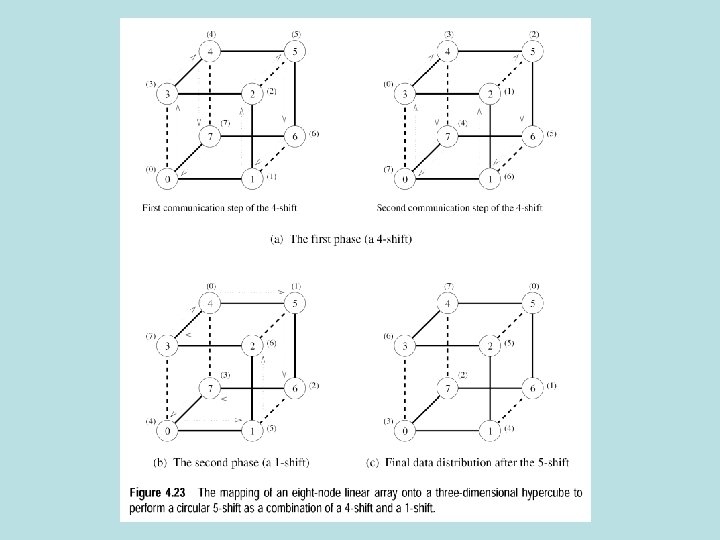
Circular shift on hypercube • Map linear array onto hypercube: map I to j, where j is the d bit reflected Gray code of i

What happens if we split messages into packets? • One to all broadcast: scatter operation followed by all to all broadcast • Scatter: tslogp p + tw(m/p)(p-1) • All to all of messages of size m/p: ts log p +tw(m/p)(p-1) on a hypercube • T~2 x (ts log p + twm)on a hypercube • Bottom line-double the start-up cost, but cost of tw reduced by (log p)/2 • All to one reduction-dual of one to all broadcast, so all to all reduction followed by gather • All reduce combine the above two