BASIC ANTENNA PARAMETERS 1 Presentation Outline n n

BASIC ANTENNA PARAMETERS 1

Presentation Outline n n n n n Introduction Reflection Coefficient Impedance bandwidth Radiation patterns Field Regions Beamwidth Directivity Antenna Efficiency Antenna Gain Polarization 2

Introduction n n Antenna parameters: describe the performance of an antenna Definitions of the various parameters are necessary, and some are interrelated. Most parameters are derived from: ¨ Complex radiation pattern ¨ Gain (or efficiency) ¨ Impedance (or scattering parameters) IEEE Standard Definitions of Terms for Antennas (IEEE Std 145 – 1983) 3

Reflection Coefficient n Ratio of the reflected voltage amplitude vs the forward voltage amplitude 4

Impedance Bandwidth n A range of frequencies, within which the antenna characteristics (input impedance) conforms to certain specifications (e. g. |Γ| = -10 d. B): n For narrowband antennas, the FBW is expressed as a percentage of the frequency difference over the center frequency: 5

Radiation Pattern n Defined as “a mathematical function or a graphical representation of the radiation properties of the antenna as a function of space coordinates. n Is determined in the far-field region. n Represented as a function of the directional coordinates. n Radiation properties include power flux density, radiation intensity, field strength, directivity, phase or polarization. ” 6

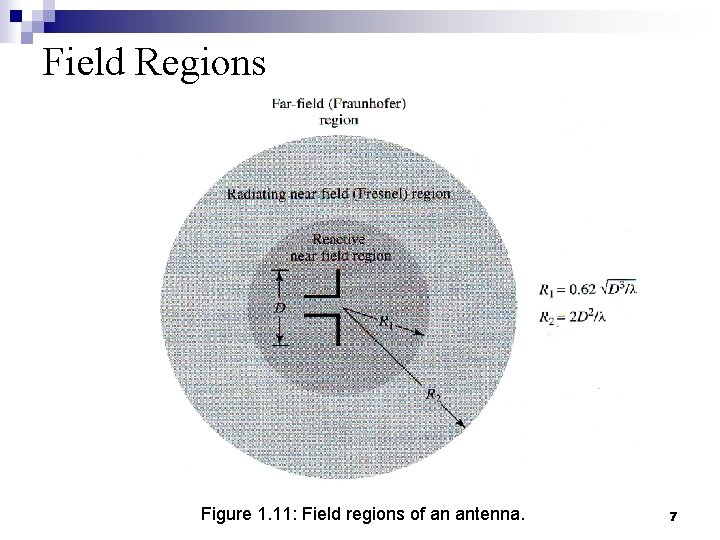
Field Regions Figure 1. 11: Field regions of an antenna. 7

Field Regions n Reactive near-field region is defined as “that portion of the near-field region immediately surrounding the antenna wherein the reactive field predominates”. [1. 10] where λ is the wavelength D is the largest dimension of the antenna n For a very short dipole (or equivalent radiator) the outer boundary is commonly taken to exist at a distance λ/2π from the antenna surface. 8

Field Regions n Radiating near-field region (Fresnel) is defined as “that region of the field of an antenna between the reactive near-field region and the far-field region wherein radiation fields predominate and wherein the angular field distribution is dependent upon the distance from the antenna”. [1. 11] where λ is the wavelength D is the largest dimension of the antenna n If antenna has a dimension that is not large compared to wavelength, this region may not exist. 9

Field Regions n Far-field region (Fraunhofer) is defined as “that region of the field of an antenna where the angular field distribution is essentially independent of the distance from the antenna”. [1. 12] where λ is the wavelength D is the largest dimension of the antenna n The far-field patterns of certain antennas, such as multibeam reflector antennas are sensitive to variations in phase over their apertures. 10

Field Regions Typical changes of antenna amplitude pattern shape from reactive near field 11 toward the far field.

Radiation Pattern: Types of Radiation Patterns: Power pattern: the trace of the angular variation of the received/radiated power at a constant radius from the antenna ¨ Amplitude field pattern: the trace of the spatial variation of the magnitude of electric (magnetic) field at a constant radius from the antenna. ¨ n n Often the field and power pattern are normalized with respect to their maximum value, yielding normalized field and power patterns. The power pattern is usually plotted on a logarithmic scale or more commonly in decibels (d. B). 12

Radiation Pattern: Types n For an antenna, the ¨ Field pattern (in linear scale) typically represents a plot of the magnitude of the electric or magnetic field as a function of the angular space. ¨ Power pattern (in linear scale) typically represents a plot of the square of the magnitude of the electric or magnetic field as a function of the angular space. ¨ Power pattern (in d. B) represents the magnitude of the electric or magnetic field, in decibels, as a function of the angular space. n Note: the power pattern and the amplitude field pattern 13 are the same when computed and plotted in d. B.

Radiation Pattern: Example Figure 1. 1: coordinate system for antenna analysis 14

Radiation Pattern: Example 3 D & 2 D Three and two dimensional power patterns (in linear scale) 15

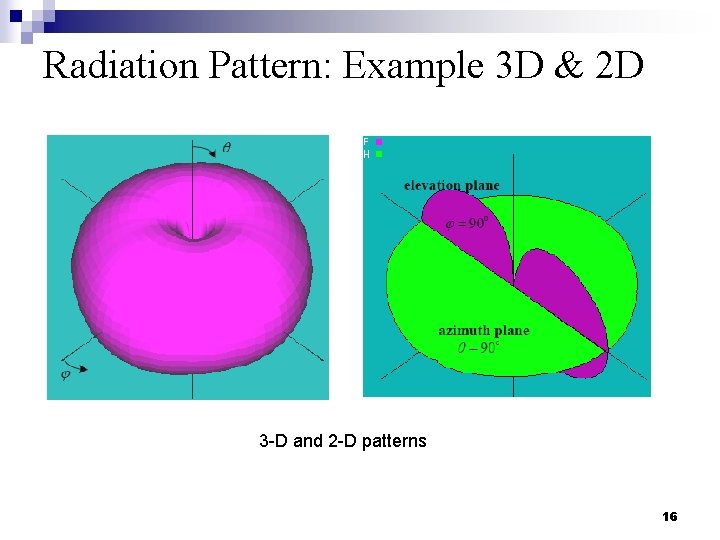
Radiation Pattern: Example 3 D & 2 D 3 -D and 2 -D patterns 16

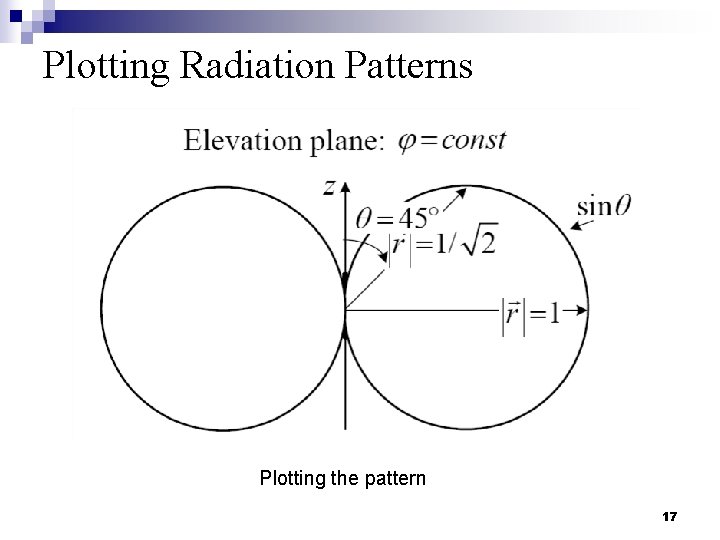
Plotting Radiation Patterns Plotting the pattern 17

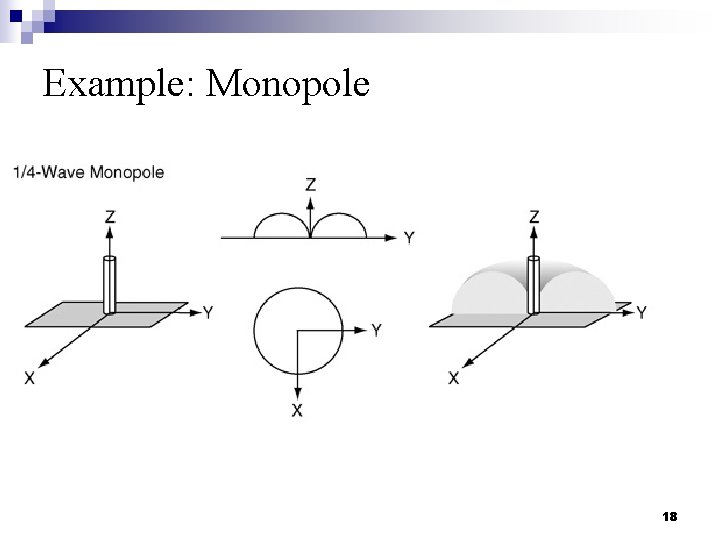
Example: Monopole 18

Example: Yagi antenna 19

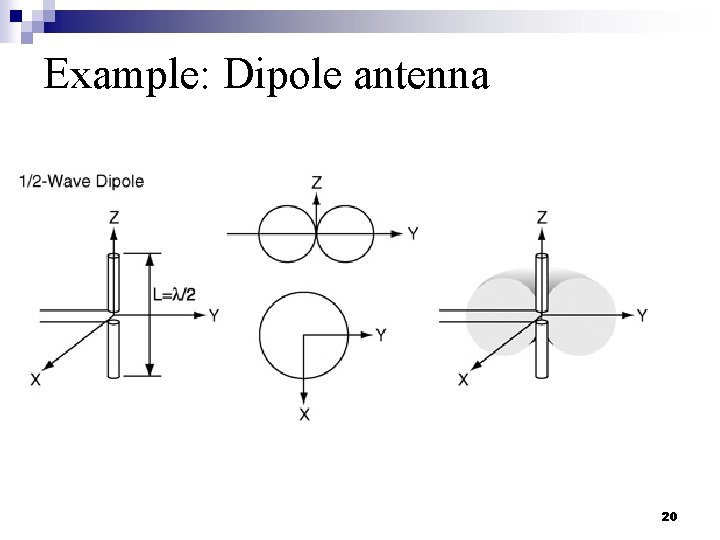
Example: Dipole antenna 20

Radiation Pattern Characteristics n n n The plus (+) and the minus (-) signs in the lobes indicate the relative polarization of the amplitude between the various lobes, which changes (alternates) as the nulls are crossed. To find the points where the pattern achieves its half -power (-3 d. B points), relative to the maximum value of the pattern: ¨ Field pattern at 0. 707 value of its maximum. ¨ Power pattern (in linear scale) at its 0. 5 value of its maximum. ¨ Power pattern (in d. B) at -3 d. B value of its maximum. The angular separation between the two half-power points is referred to as HPBW. 21

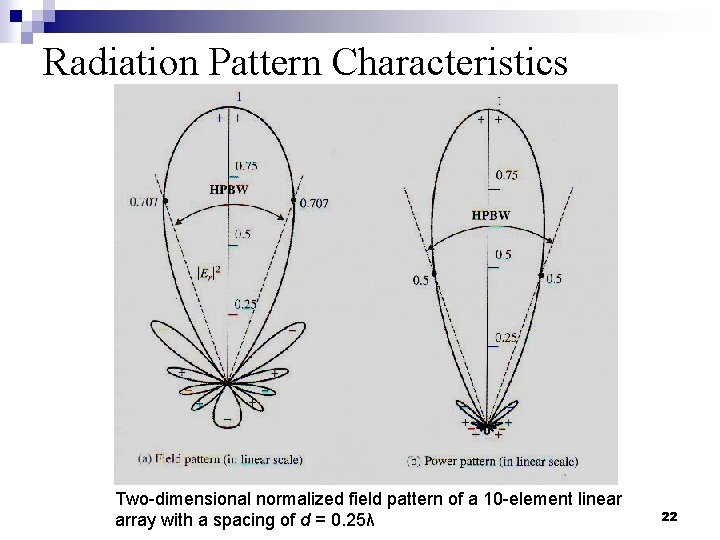
Radiation Pattern Characteristics Two-dimensional normalized field pattern of a 10 -element linear array with a spacing of d = 0. 25λ 22

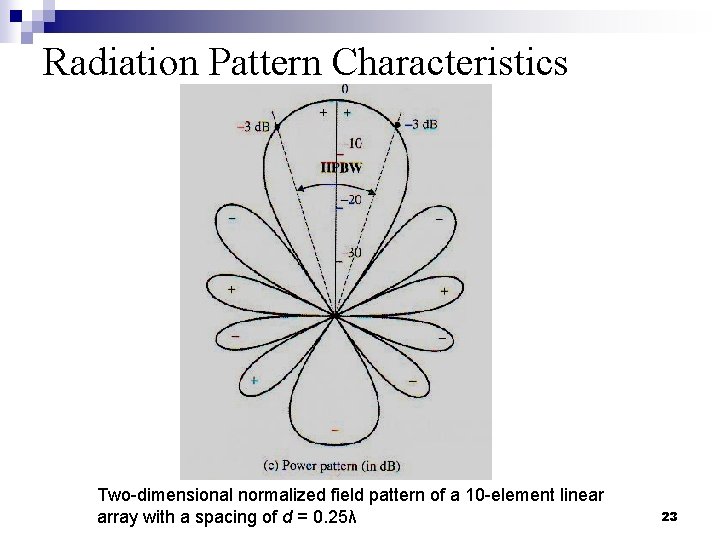
Radiation Pattern Characteristics Two-dimensional normalized field pattern of a 10 -element linear array with a spacing of d = 0. 25λ 23

Beamwidth • Defined as the angular separation between two identical points on opposite side of the pattern maximum. • The Half-Power Beamwidth (HPBW): in a plane containing the direction of the maximum of a beam. • First-Null Beamwidth (FNBW): the angular separation between the first nulls if the pattern. Often FNBW≈2⋅HPBW • Used as a trade-off between it and the side lobe level; as the beamwidth decreases, the side lobe increases and vice-versa. • Used to describe the resolution capabilities of the antenna; to distinguish between two adjacent radiating sources and targets. 24

Beamwidth Pattern beamwidth. 25

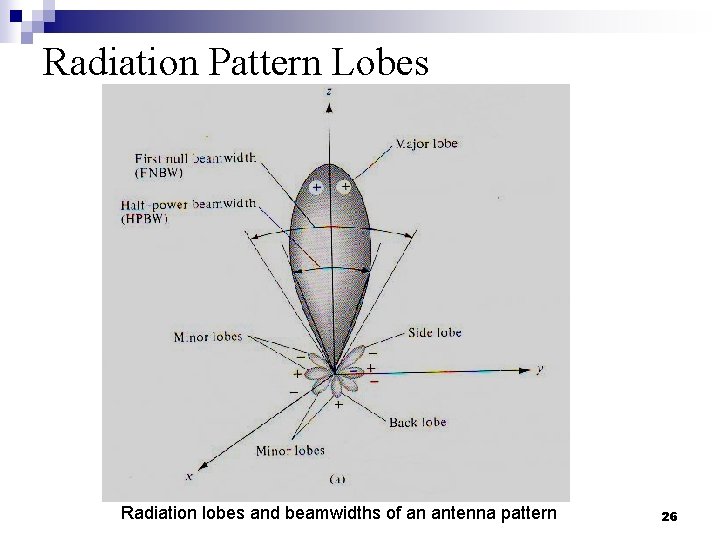
Radiation Pattern Lobes Radiation lobes and beamwidths of an antenna pattern 26

Radiation Pattern Lobes n n A major lobe (also called main beam) is defined as “the radiation lobe containing the direction of maximum radiation”. A minor lobe is any lobe except major lobe. represent radiation in undesired directions, and they should be minimized A side lobe is “a radiation lobe in any direction other than intended lobe”. Normally adjacent to the main lobe and occupies the hemisphere in the direction of the main beam. Largest of the minor lobes. A back lobe is “a radiation lobe whose axis makes an angle of approximately 180º with respect to the beam of the antenna”. 27

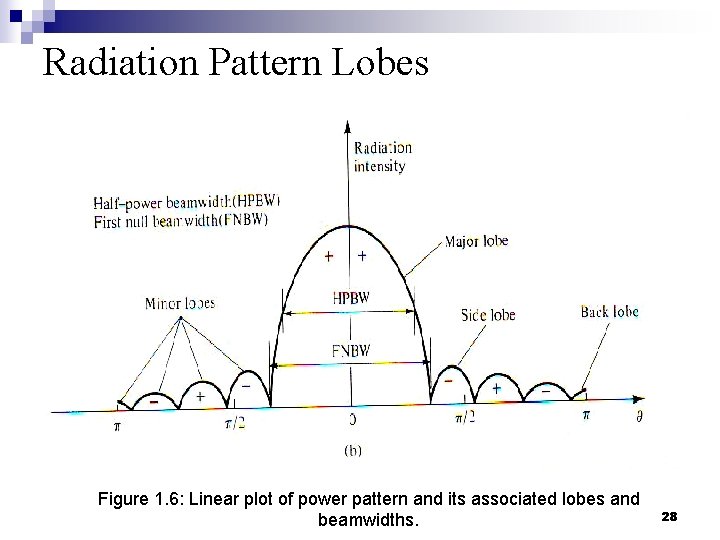
Radiation Pattern Lobes Figure 1. 6: Linear plot of power pattern and its associated lobes and beamwidths. 28

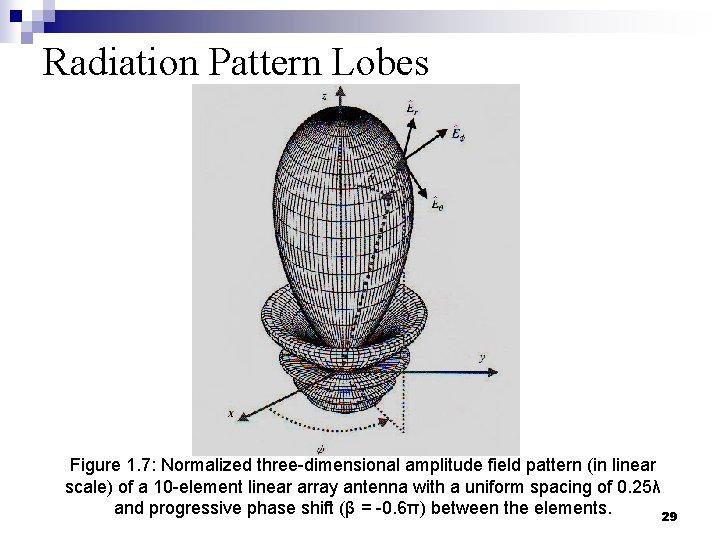
Radiation Pattern Lobes Figure 1. 7: Normalized three-dimensional amplitude field pattern (in linear scale) of a 10 -element linear array antenna with a uniform spacing of 0. 25λ and progressive phase shift (β = -0. 6π) between the elements. 29

Isotropic/Directional/Omnidirectional Patterns n Isotropic pattern ¨ is the pattern of an antenna having equal radiation in all directions. ¨ This is an ideal (not physically achievable) concept. ¨ Used to define other antenna parameters. ¨ It is represented simply by a sphere whose center coincides with the location of the isotropic radiator. n Directional antenna ¨ is an antenna, which radiates (receives) much more efficiently in some directions than in others. ¨ Applies to antennas whose directivity is much higher than that of a half wavelength dipole. 30

Isotropic/Directional/Omnidirectional Patterns n Omnidirectional antenna ¨ is an antenna, which has a non-directional pattern in a given plane, and a directional pattern in any orthogonal plane (e. g. single-wire antennas). 31

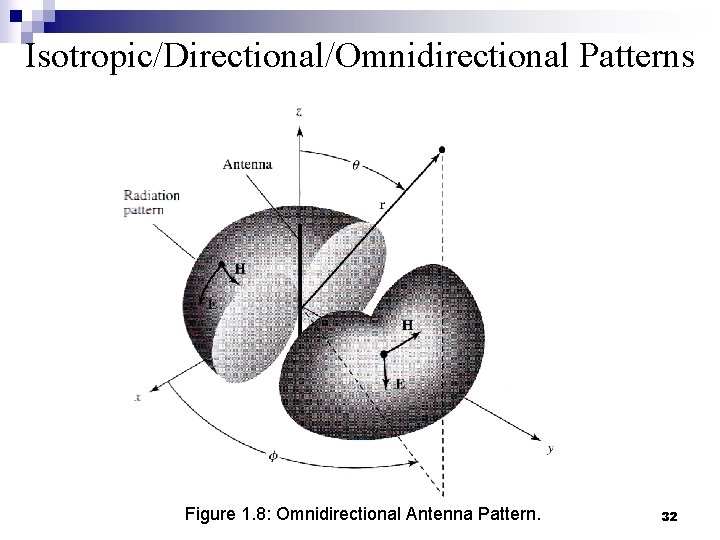
Isotropic/Directional/Omnidirectional Patterns Figure 1. 8: Omnidirectional Antenna Pattern. 32

Principal Patterns n Principal patterns are the 2 -D patterns of linearly polarized antennas, measured in the E-plane (a plane parallel to the |Ē| vector and containing the direction of maximum radiation) n the H-plane (a plane parallel to the vector, orthogonal to the E-plane, and containing the direction of maximum radiation). 33

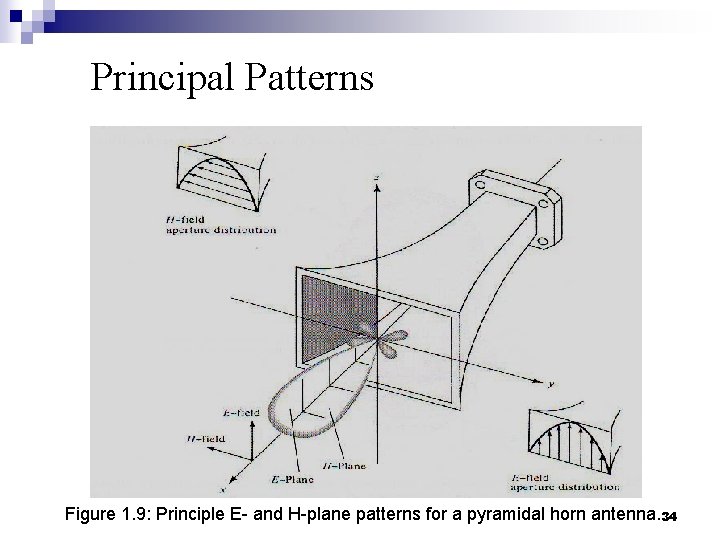
Principal Patterns Figure 1. 9: Principle E- and H-plane patterns for a pyramidal horn antenna. 34

Polarization n n The polarization of the wave can be defined in terms of a wave radiated (transmitted) or received by an antenna in a given direction. Polarization may be classified as linear, circular or elliptical. If the vector that describes the electric field at a point in space as a function of time is always directed along a line, the field is said to be linearly polarized. If the figure that the electric field traces is an ellipse, the field is said to be elliptically polarized. Linear and circular polarizations are special cases of elliptical, and they can be obtained when the ellipse become a straight line or a circle, respectively. 35

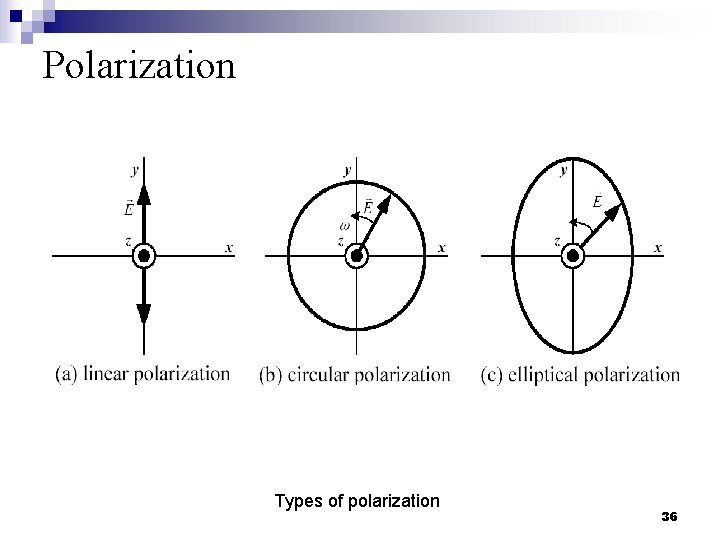
Polarization Types of polarization 36

Polarization n Polarization of an antenna in a given direction is defined as “the polarization of the wave transmitted (radiated) by the antenna. When the direction is not stated, the polarization is taken to be the polarization in the direction of maximum gain”. n Polarization of a radiated wave is defined as “that property of an electromagnetic wave describing the time varying direction and relative magnitude of the electric field vector. n Polarization is the curve traced by the end point of the arrow (vector) representing the instantaneous electric field. The field must be observed along the direction of propagation. 37

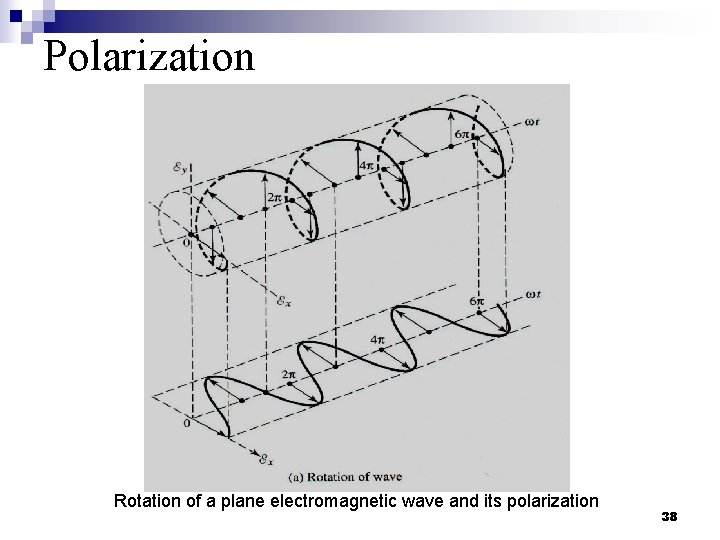
Polarization Rotation of a plane electromagnetic wave and its polarization 38

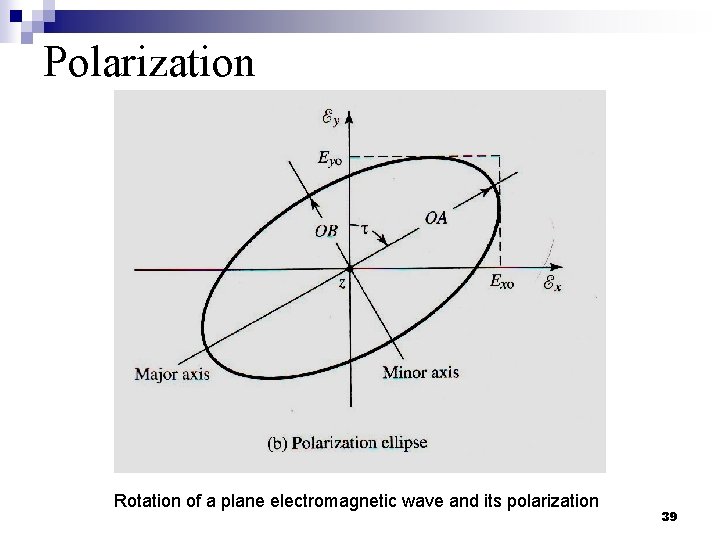
Polarization Rotation of a plane electromagnetic wave and its polarization 39

Polarization n At each point on the radiation sphere, the polarization is usually resolved into a pair of orthogonal polarizations, the co-polarization and cross-polarization. n Co-polarization represents the polarization the antenna is intended to radiate (receive) while crosspolarization represents the polarization orthogonal to the co-polarization 40

Radiation Pattern Measurement 41

Radiation Pattern Measurement 42

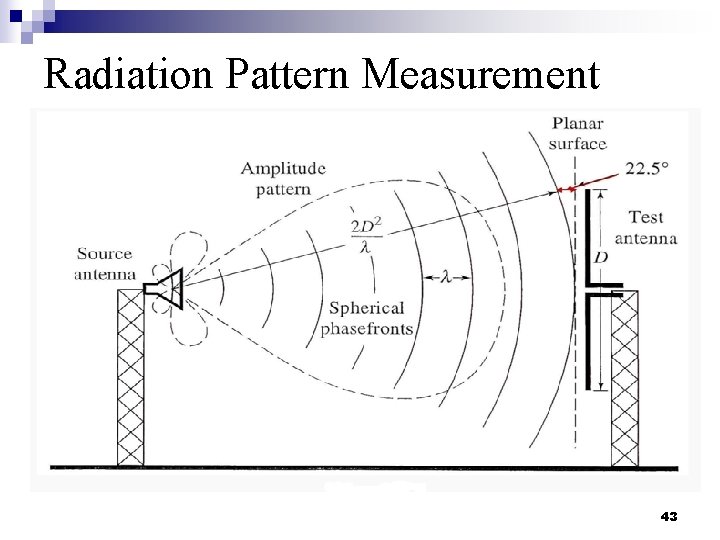
Radiation Pattern Measurement 43

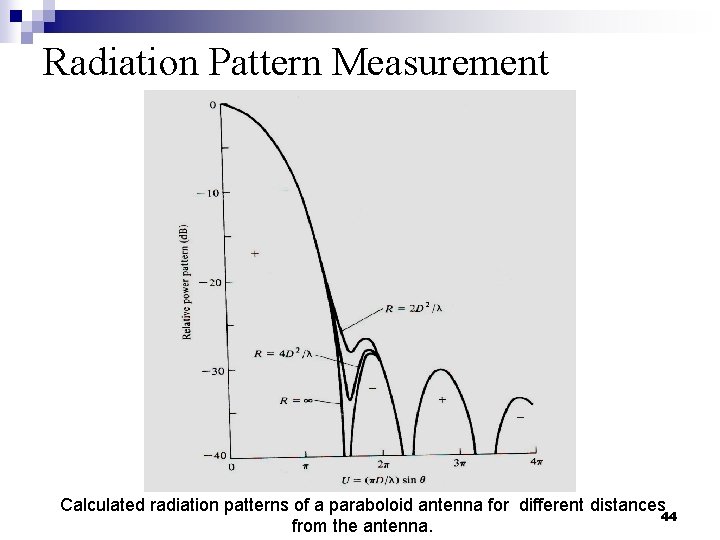
Radiation Pattern Measurement Calculated radiation patterns of a paraboloid antenna for different distances 44 from the antenna.

Directivity • Defined as “the ratio of the radiation intensity in a given direction from the antenna to the radiation intensity averaged over all directions. ” • “The average radiation intensity is equal to the total power radiated by the antenna divided by 4π. ” • If the direction is not specified, the direction of maximum radiation intensity is implied. ” • The directivity of a non-isotropic source is equal to the ratio of its radiation intensity in a given direction over that of an isotropic source. 45

Directivity • If the direction is not specified, it implies the direction of maximum radiation intensity (maximum directivity) expressed as: [1. 28] D = directivity (dimensionless) D 0 = maximum directivity (dimensionless) U = radiation intensity (W / unit solid angle) Umax = maximum radiation intensity (W / unit solid angle) U 0 = radiation intensity of isotropic source (W / unit solid angle) Prad = total radiated power (W) 46

Antenna Efficiency n n n Total efficiency of an antenna et is used to estimate the total loss of energy at the input terminals of the antenna and within the antenna structure. Includes all mismatch losses and the dielectric/conduction losses (described by the radiation efficiency, e, as defined by the IEEE Standards) The overall efficiency: e 0 = total efficiency (dimensionless) er = reflection (missmatch) efficiency (dimensionless) ec = conduction efficiency (dimensionless) ed = dielectric efficiency (dimensionless) Γ = voltage reflection coefficient at the input terminals of the antenna. 47

Antenna Efficiency Reference terminals and losses of an antenna 48

Antenna Gain • G is the ratio of the radiation intensity U in a given direction and the radiation intensity that would be obtained, if the power fed to the antenna were radiated isotropically. • Normally we deal with relative gain. • Defined as “the ratio of the power gain in a given direction to the power gain of a reference antenna in its referenced direction”. • The power input must be same for both antennas. 49

Antenna Gain n The reference antenna usually a dipole, horn, or any other antenna whose gain can be calculated or it is known. n When the direction is not stated, the power gain is usually taken in the direction of maximum radiation. 50

Gain Measurement n Popular: Gain comparison/substitution method n A standard gain antenna (with known gain) is used to calculate the gain of the antenna under test (AUT) n From the Friis Transmission equation: 51

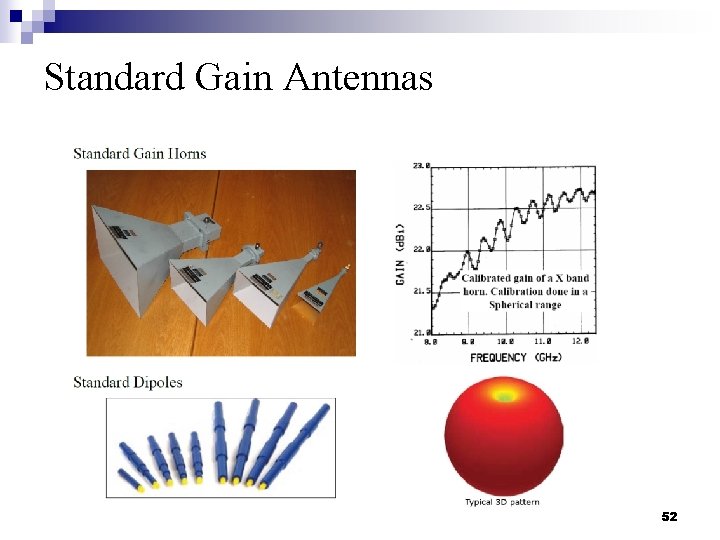
Standard Gain Antennas 52

Gain Measurement n Step 1: Measure the standard gain antenna (SGH) as the AUT n Step 2: Measure the AUT 53

Gain Measurements n Step 3: Gain of AUT can be calculated using: n Note: n Tx and AUT needs to be co-polarized n AUT need to be placed in the far field 54

Extra Slides 55

Radian & Steradian • The measure of a plane angle is a radian. • One radian is defined as the plane angle with its vertex at the center of a circle of radius r that is subtended by an arc whose length is r. • There are 2π rad (2πr/r) in a full circle. 56

Radian & Steradian • The measure of a solid angle is a steradian. • One steradian is defined as the solid angle with its vertex at the center of a circle of a sphere radius r that is subtended by a spherical surface area equal to that of square which each side of a length r. • There are 4π sr (4πr 2/r 2) in a closed sphere. 57

Radian & Steradian The infinitesimal area d. A on the surface of a sphere of radius r, is given by: (m 2) Therefore, the element of solid angle dΩ of a sphere can be written as: (sr) 58

Radian & Steradian Geometrical arrangements for defining a radian and a steradian 59