Baseband Signaling and Modulation Part 1 Baseband Signaling

Baseband Signaling and Modulation Part 1: Baseband Signaling Part 1 of a 2 -part presentation Eric L. Michelsen Inductive Logic
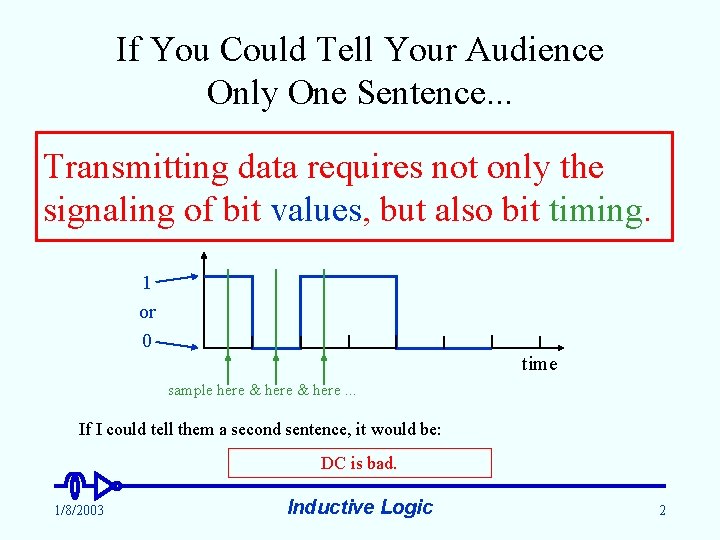
If You Could Tell Your Audience Only One Sentence. . . Transmitting data requires not only the signaling of bit values, but also bit timing. 1 or 0 time sample here & here. . . If I could tell them a second sentence, it would be: DC is bad. 1/8/2003 Inductive Logic 2

Topics: Baseband Signaling (day 1) • • • On-Off signaling Antipodal signaling Timing recovery NRZI Multilevel: 2 B 1 Q DS 1 & DS 3 • • Cosine review Sums of cosines Spectra Fourier transforms Baseband signaling Why cosine waves? Transfer functions • • • Manchester encoding 4 B/5 B encoding 8 B/10 B encoding Multi-Level Transition A modern line code Topics: Modulation (day 2) 1/8/2003 • • • Communication channels as filters Amplitude modulation Amplitude demodulation Quadrature multiplexing DMT ADSL Inductive Logic 3
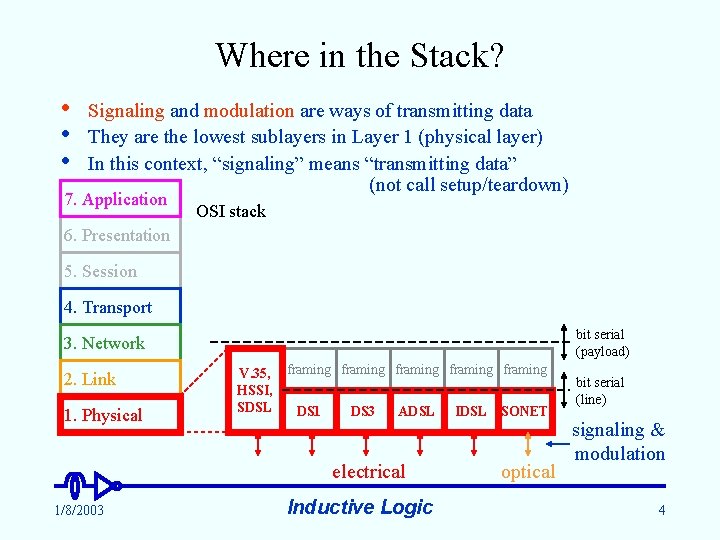
Where in the Stack? • • • Signaling and modulation are ways of transmitting data They are the lowest sublayers in Layer 1 (physical layer) In this context, “signaling” means “transmitting data” (not call setup/teardown) 7. Application OSI stack 6. Presentation 5. Session 4. Transport bit serial (payload) 3. Network 2. Link 1. Physical V. 35, HSSI, SDSL framing framing DS 1 DS 3 ADSL electrical 1/8/2003 Inductive Logic IDSL SONET optical bit serial (line) signaling & modulation 4
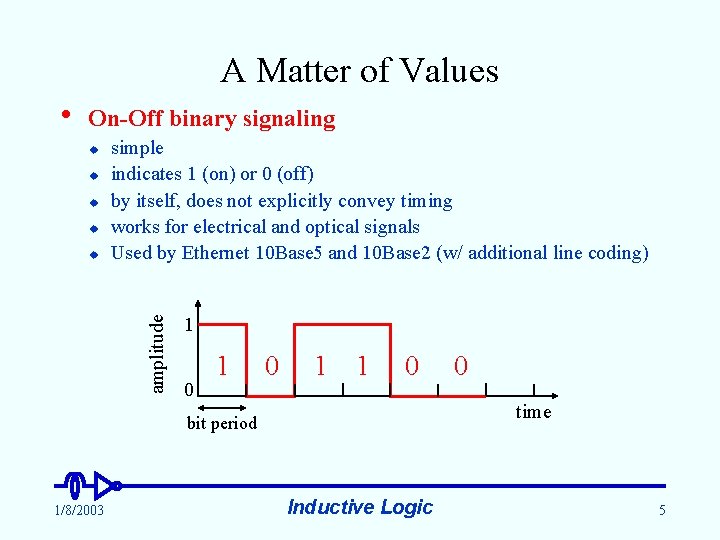
A Matter of Values • On-Off binary signaling u u amplitude u simple indicates 1 (on) or 0 (off) by itself, does not explicitly convey timing works for electrical and optical signals Used by Ethernet 10 Base 5 and 10 Base 2 (w/ additional line coding) 1 0 1 1 0 time bit period 1/8/2003 0 Inductive Logic 5
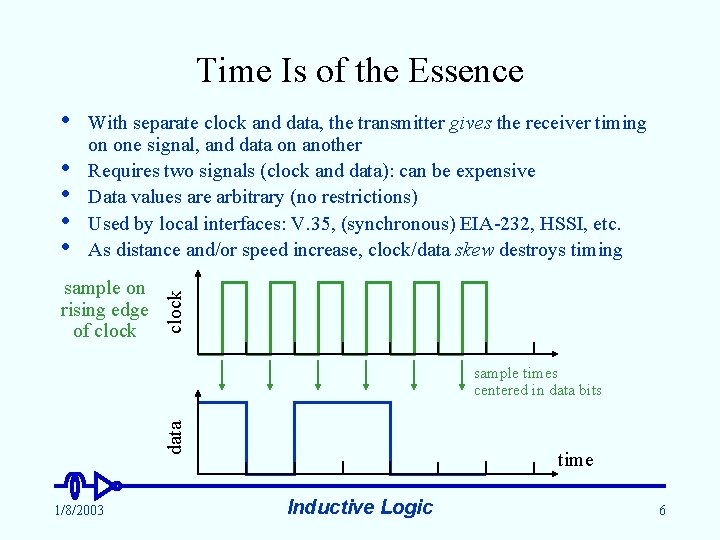
Time Is of the Essence • • With separate clock and data, the transmitter gives the receiver timing on one signal, and data on another Requires two signals (clock and data): can be expensive Data values are arbitrary (no restrictions) Used by local interfaces: V. 35, (synchronous) EIA-232, HSSI, etc. As distance and/or speed increase, clock/data skew destroys timing sample on rising edge of clock • data sample times centered in data bits 1/8/2003 time Inductive Logic 6

• • No Clock: Do You Know Where Your Data Is? Most long-distance or high speed signaling is self timed: it has no separate clock; the receiver recovers timing from the data itself Receiver knows the nominal data rate, but requires transitions in the signal to locate the bits, and interpolate the sample points Receiver tracks the timing continuously, to stay in synch u Tracking requires sufficient transition density throughout the data stream Used in all DSLs, DS 1, DS 3, SONET, all Ethernets, etc. data transitions locate data interpolated sample times (bit centers) 1/8/2003 Inductive Logic time 7

Timing Recovery • All self-timed line codes provide sufficient signal transitions for timing recovery. Some methods used: u u u u 1/8/2003 Scrambling Return to zero (RTZ) Zero substitution Manchester encoding 4 B/5 B 8 B/10 B Multi-level transition Inductive Logic 8

All For One. . . or Zero • amplitude • • • On-Off binary signaling: simple, but not energy efficient (SNR) At unit distance (A = 1), average energy = A 2/2 = 0. 5 For balanced data, DC (Direct Current) ~= 0. 5 (bad) Also known as Non-Return to Zero (NRZ) Requires sufficient data transition density, or scrambling Works for electrical and optical signals 1 0 distance 1 0 1 1 0 time bit period 1/8/2003 0 Inductive Logic 9
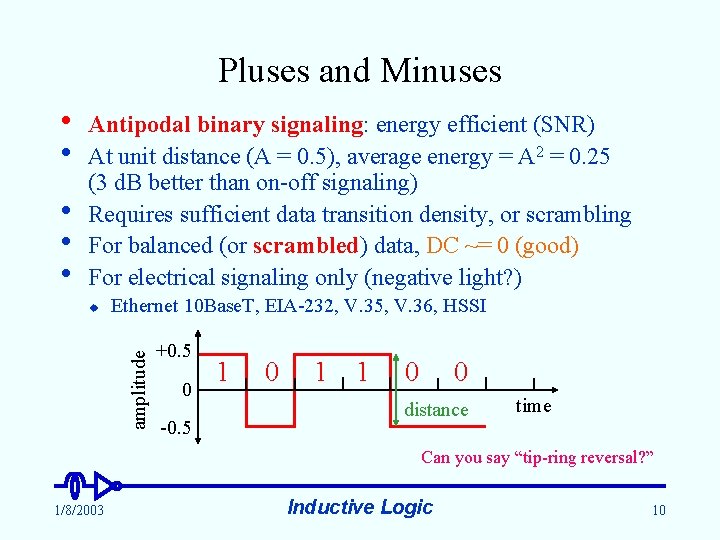
Pluses and Minuses • • • Antipodal binary signaling: energy efficient (SNR) At unit distance (A = 0. 5), average energy = A 2 = 0. 25 (3 d. B better than on-off signaling) Requires sufficient data transition density, or scrambling For balanced (or scrambled) data, DC ~= 0 (good) For electrical signaling only (negative light? ) Ethernet 10 Base. T, EIA-232, V. 35, V. 36, HSSI amplitude u +0. 5 0 -0. 5 1 0 1 1 0 0 distance time Can you say “tip-ring reversal? ” 1/8/2003 Inductive Logic 10
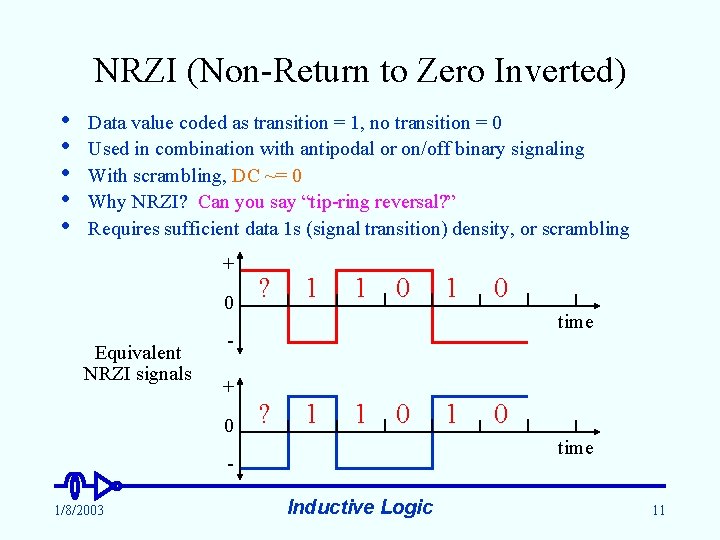
NRZI (Non-Return to Zero Inverted) • • • Data value coded as transition = 1, no transition = 0 Used in combination with antipodal or on/off binary signaling With scrambling, DC ~= 0 Why NRZI? Can you say “tip-ring reversal? ” Requires sufficient data 1 s (signal transition) density, or scrambling + 0 Equivalent NRZI signals ? 1 1 0 0 time + 0 ? 1 1 0 time 1/8/2003 1 Inductive Logic 11
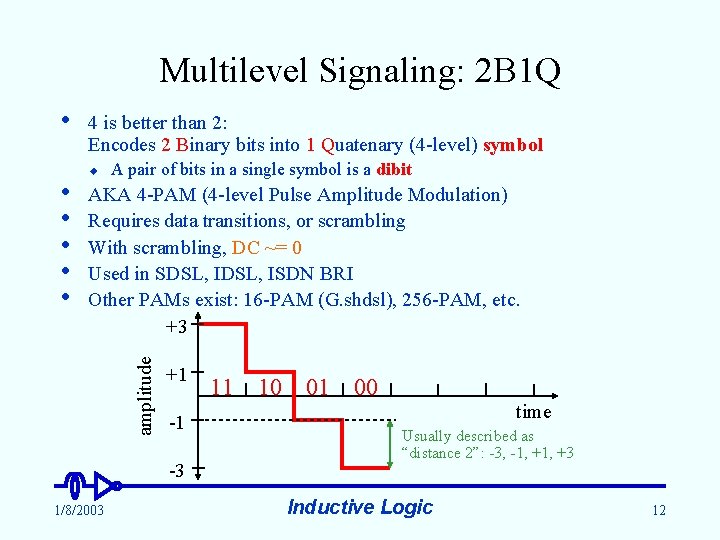
Multilevel Signaling: 2 B 1 Q • u A pair of bits in a single symbol is a dibit AKA 4 -PAM (4 -level Pulse Amplitude Modulation) Requires data transitions, or scrambling With scrambling, DC ~= 0 Used in SDSL, ISDN BRI Other PAMs exist: 16 -PAM (G. shdsl), 256 -PAM, etc. +3 amplitude • • • 4 is better than 2: Encodes 2 Binary bits into 1 Quatenary (4 -level) symbol +1 -1 -3 1/8/2003 11 10 01 00 time Usually described as “distance 2”: -3, -1, +3 Inductive Logic 12
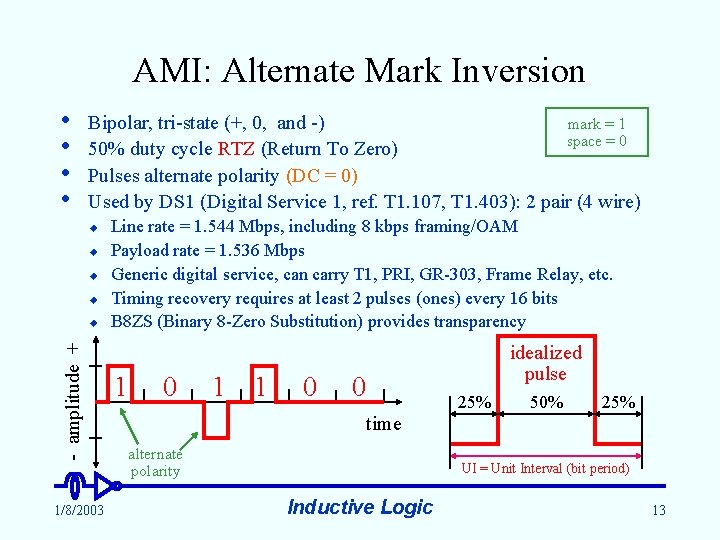
AMI: Alternate Mark Inversion • • mark = 1 Bipolar, tri-state (+, 0, and -) space = 0 50% duty cycle RTZ (Return To Zero) Pulses alternate polarity (DC = 0) Used by DS 1 (Digital Service 1, ref. T 1. 107, T 1. 403): 2 pair (4 wire) u u - amplitude + u 1/8/2003 Line rate = 1. 544 Mbps, including 8 kbps framing/OAM Payload rate = 1. 536 Mbps Generic digital service, can carry T 1, PRI, GR-303, Frame Relay, etc. Timing recovery requires at least 2 pulses (ones) every 16 bits B 8 ZS (Binary 8 -Zero Substitution) provides transparency 1 0 1 1 0 idealized pulse 0 time alternate polarity 25% 50% 25% UI = Unit Interval (bit period) Inductive Logic 13
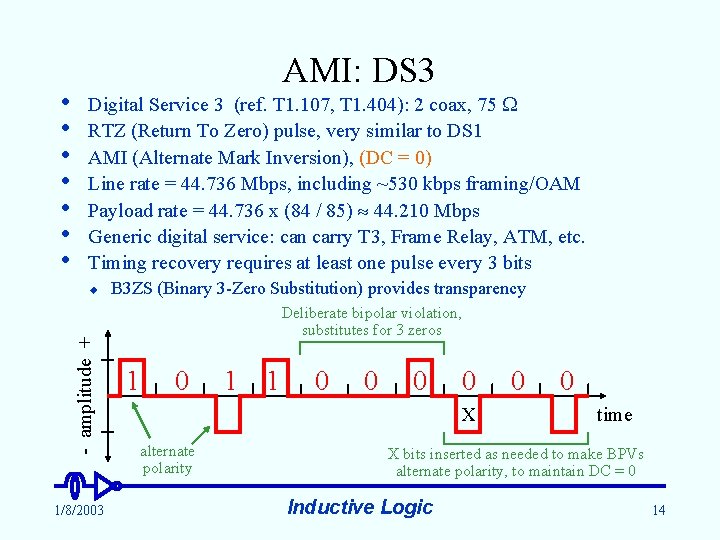
• • AMI: DS 3 Digital Service 3 (ref. T 1. 107, T 1. 404): 2 coax, 75 RTZ (Return To Zero) pulse, very similar to DS 1 AMI (Alternate Mark Inversion), (DC = 0) Line rate = 44. 736 Mbps, including ~530 kbps framing/OAM Payload rate = 44. 736 x (84 / 85) 44. 210 Mbps Generic digital service: can carry T 3, Frame Relay, ATM, etc. Timing recovery requires at least one pulse every 3 bits - amplitude + u 1/8/2003 B 3 ZS (Binary 3 -Zero Substitution) provides transparency Deliberate bipolar violation, substitutes for 3 zeros 1 0 1 1 0 0 X alternate polarity 0 0 time X bits inserted as needed to make BPVs alternate polarity, to maintain DC = 0 Inductive Logic 14
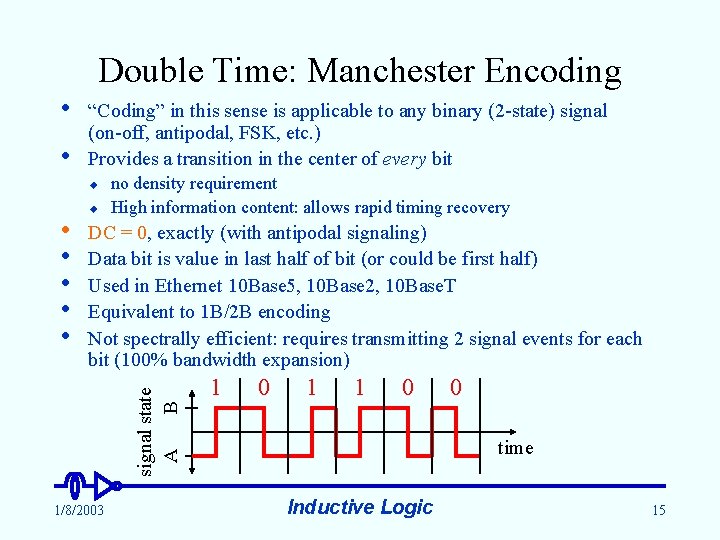
Double Time: Manchester Encoding • • “Coding” in this sense is applicable to any binary (2 -state) signal (on-off, antipodal, FSK, etc. ) Provides a transition in the center of every bit u DC = 0, exactly (with antipodal signaling) Data bit is value in last half of bit (or could be first half) Used in Ethernet 10 Base 5, 10 Base 2, 10 Base. T Equivalent to 1 B/2 B encoding Not spectrally efficient: requires transmitting 2 signal events for each bit (100% bandwidth expansion) signal state A B • • • u no density requirement High information content: allows rapid timing recovery 1/8/2003 1 0 1 1 0 0 time Inductive Logic 15

Enough is Enough: 4 B/5 B Encoding • • Encodes 4 payload bits into 5 line bits Guarantees transitions; no user data restrictions or scrambling needed Extra codewords available for control (Idle, SSD, ESD, . . . ) More BW efficient than Manchester: 25% expansion Data DC >> 0 (bad), but used with NRZI or MLT, DC ~= 0 0 1 1 0 1 0 0 1 Checks line integrity by counting invalid codes 2 1 0 0 Used in Ethernet 100 Base. TX, FDDI 3 1 0 1 Control 1/8/2003 1 1 1 IDLE used as inter-stream fill code 1 1 0 0 0 J 1 0 0 0 1 K 0 1 1 0 1 T 0 0 1 1 1 R Start-of-Stream Delimiter, Part 1 of 2; always used in pairs with K Start-of-Stream Delimiter, Part 2 of 2; always used in pairs with J End-of-Stream Delimiter, Part 1 of 2; always used in pairs with R End-of-Stream Delimiter, Part 2 of 2; always used in pairs with T Inductive Logic 4 5 6 7 8 9 A B C D E F 0 0 1 1 1 0 0 1 1 0 0 1 1 1 0 0 0 1 0 1 0 1 16

• • • Twice as Good: 8 B/10 B Encoding Encodes 8 payload bits into 10 line bits Guarantees 3 to 8 transitions per 10 -bit codeword Maximum run-length of 5 25% BW expansion (same as 4 B/5 B) 12 control codes (start of packet, end of packet, error, etc. ) Alternately inverts non-zero-DC codewords to achieve zero DC (similar to AMI) u • • Worst case codeword imbalance is 6/4 Checks line integrity by counting invalid codes Used in Gigabit Ethernet, Fiber Channel (FC), some backplanes 1/8/2003 Inductive Logic 17
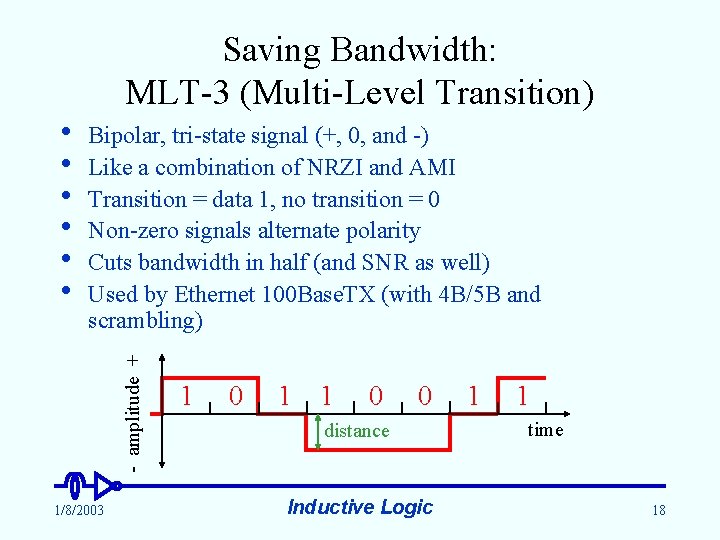
Saving Bandwidth: MLT-3 (Multi-Level Transition) Bipolar, tri-state signal (+, 0, and -) Like a combination of NRZI and AMI Transition = data 1, no transition = 0 Non-zero signals alternate polarity Cuts bandwidth in half (and SNR as well) Used by Ethernet 100 Base. TX (with 4 B/5 B and scrambling) - amplitude + • • • 1/8/2003 1 0 1 1 0 0 distance Inductive Logic 1 1 time 18
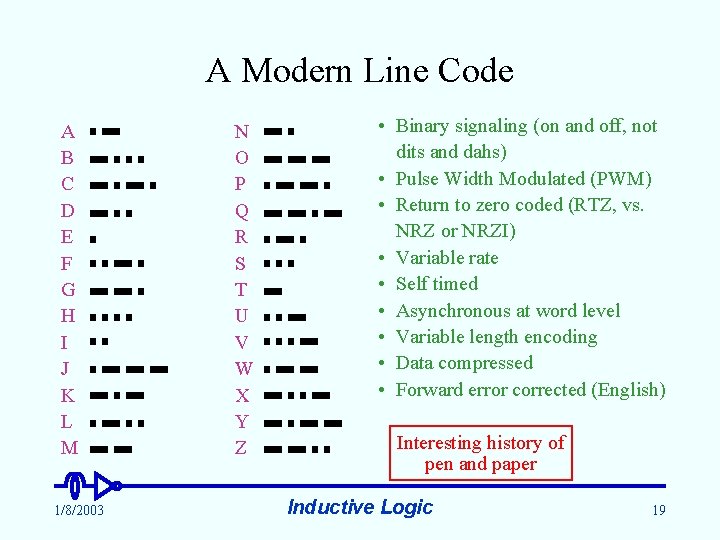
A Modern Line Code A B C D E F G H I J K L M 1/8/2003 N O P Q R S T U V W X Y Z • Binary signaling (on and off, not dits and dahs) • Pulse Width Modulated (PWM) • Return to zero coded (RTZ, vs. NRZ or NRZI) • Variable rate • Self timed • Asynchronous at word level • Variable length encoding • Data compressed • Forward error corrected (English) Interesting history of pen and paper Inductive Logic 19
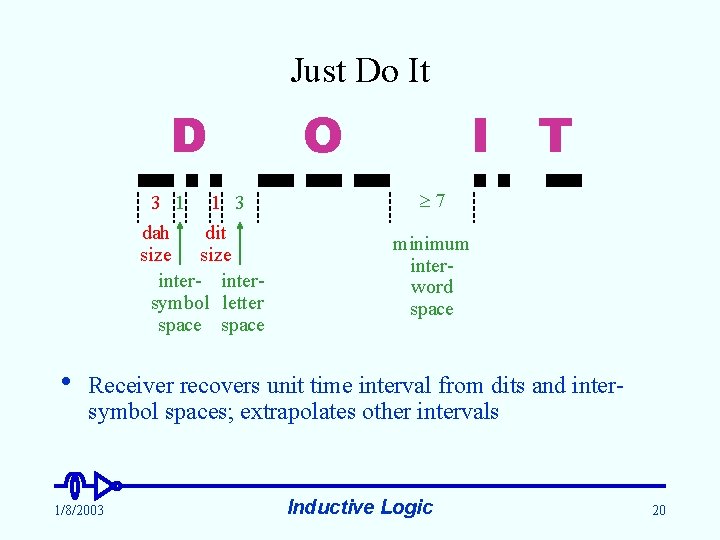
Just Do It D 3 1 1 3 dah dit size inter- intersymbol letter space • O I T 7 minimum interword space Receiver recovers unit time interval from dits and intersymbol spaces; extrapolates other intervals 1/8/2003 Inductive Logic 20

Data Compression: English size A 8 B 12 C 14 D 10 E 4 F 12 G 12 H 10 I 6 J 16 K 12 L 12 M 10 frequency. 082. 014. 028. 038. 131. 029. 020. 053. 063. 001. 004. 034. 025 avg. . 65. 17. 39. 38. 52. 35. 24. 53. 38. 02. 05. 41. 25 size frequency N 8. 071 O 14. 080 P 14. 020 Q 16. 001 R 10. 068 S 8. 061 T 6. 105 U 10. 025 V 12. 009 W 12. 015 X 14. 002 Y 16. 020 Z 14. 001 avg. . 57 1. 12. 28. 02. 68. 49. 63. 25. 11. 18. 02. 32. 01 Avg letter size: 11. 2 units English weighted avg letter size: 9. 0 (~20% savings) Opt. Eng. weighted avg letter size: 8. 6 (within 5%) 1/8/2003 Inductive Logic 21

optical multi-level antipodal on-off Baseband Summary 1/8/2003 Interface Signaling States Transition Coding Ethernet 10 Base 5, 10 Base 2 on-off + DC bias Manchester Morse Code on-off RTZ Ethernet 10 Base. T antipodal EIA-232, V. 35, HSSI antipodal Manchester none (NRZ, separate clock and data) Ethernet 100 Base. TX, FDDI (electrical) SDSL, ISDN BRI MLT (3 -level) 4 B/5 B, scrambled 2 B 1 Q (= 4 -PAM) scrambled G. shdsl 16 -PAM scrambled DS 1, DS 3 Gigabit Ethernet (optical), Fiber Channel SONET AMI (3 -level) RTZ, Bx. ZS on-off (optical) 8 B/10 B on-off (optical) scrambled FDDI (optical) on-off (optical) 4 B/5 B, NRZI Inductive Logic 22

Baseband Signaling and Modulation Part 2: Modulation Eric L. Michelsen 1/8/2003 Inductive Logic 23

Another Day, Another Sentence Modulation avoids baseband problems of signal overlap and DC error. If I could tell them a second sentence, it would be: Bandwidth is not capacity! If I could tell them a third sentence, it would be: Bandwidth is not capacity! But first, a review of Fourier analysis. . . 1/8/2003 Inductive Logic 24

Topics: Modulation • • Cosine review Sums of cosines Spectra Fourier transforms Baseband signaling Why cosine waves? Transfer functions 1/8/2003 • • • Communication channels as filters Amplitude modulation Amplitude demodulation Quadrature multiplexing DMT ADSL Inductive Logic 25

Definitions • Baseband signaling u u • Communicating a signal in its original form for a given medium (e. g. , audio) or Communicating a signal with components down to DC (or almost DC) Carrier modulation u u 1/8/2003 Communication based on modifying (modulating) a cosine wave signal Other forms of modulation exist (non-carrier modulation, e. g. , PAM, PWM, PCM(? ), but that’s another story) Inductive Logic 26
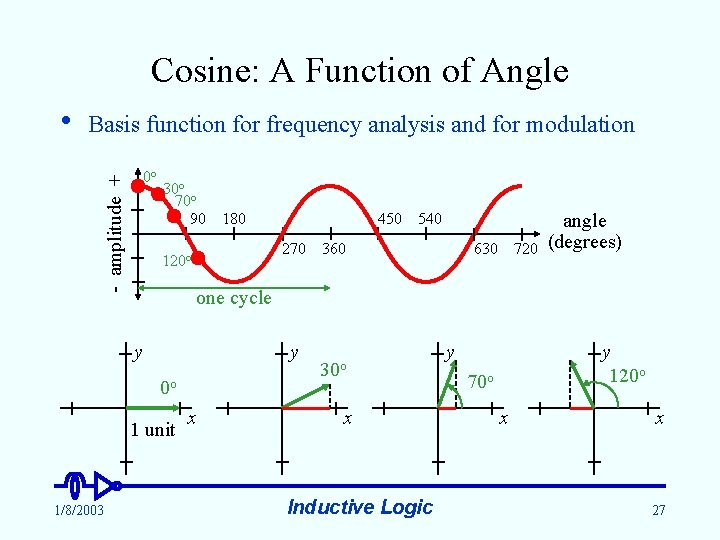
Cosine: A Function of Angle Basis function for frequency analysis and for modulation 0 o - amplitude + • 30 o o 70 90 450 270 120 o 540 360 630 720 angle (degrees) one cycle y y 0 o 1 unit 1/8/2003 180 x 30 o x Inductive Logic y y 120 o 70 o x x 27
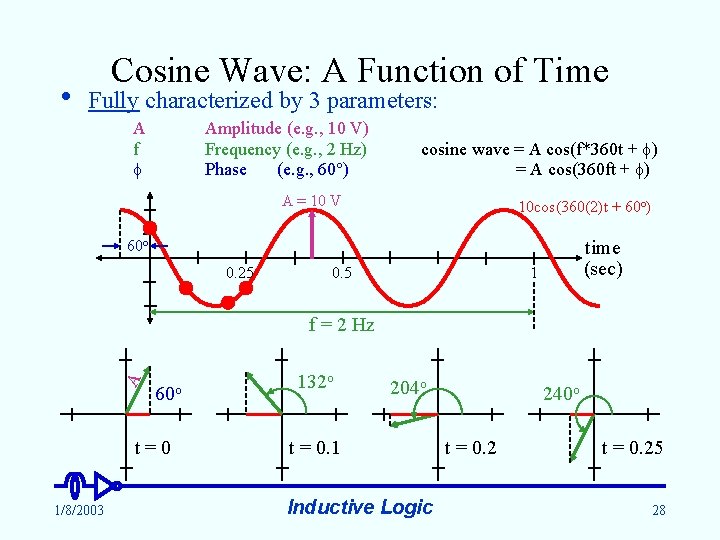
• Cosine Wave: A Function of Time Fully characterized by 3 parameters: A f Amplitude (e. g. , 10 V) Frequency (e. g. , 2 Hz) Phase (e. g. , 60 ) cosine wave = A cos(f*360 t + ) = A cos(360 ft + ) A = 10 V 10 cos(360(2)t + 60 o) time (sec) 60 o 0. 25 0. 5 1 A f = 2 Hz 60 o t=0 1/8/2003 132 o 204 o t = 0. 1 Inductive Logic 240 o t = 0. 25 28
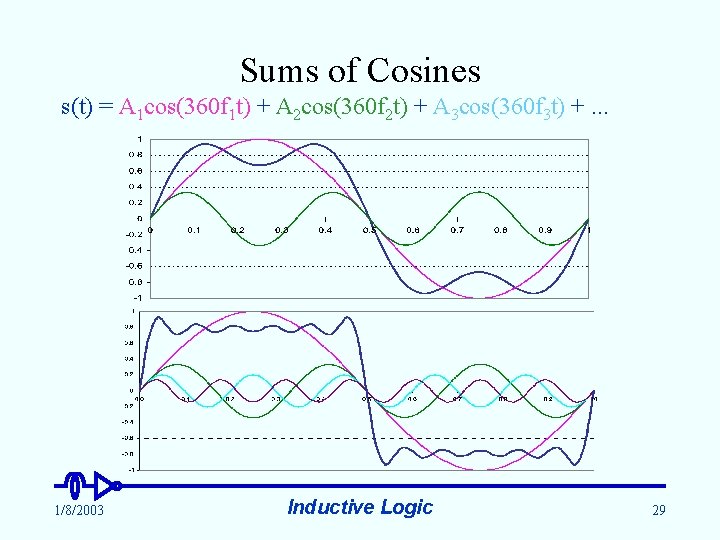
Sums of Cosines s(t) = A 1 cos(360 f 1 t) + A 2 cos(360 f 2 t) + A 3 cos(360 f 3 t) +. . . 1/8/2003 Inductive Logic 29
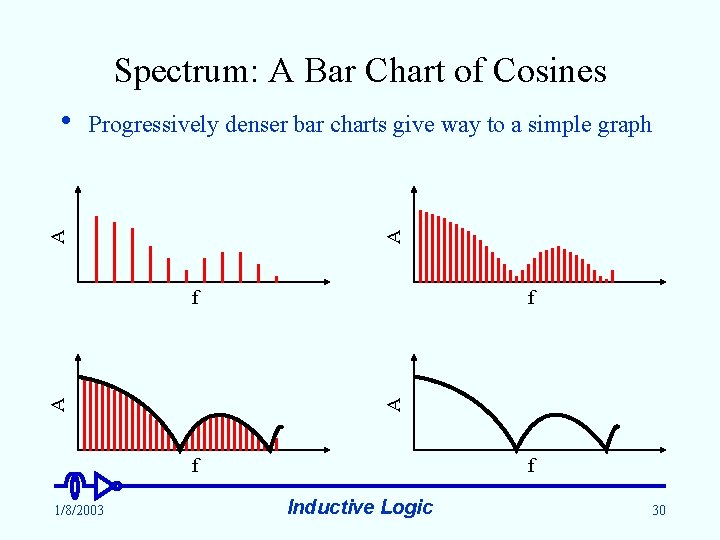
Spectrum: A Bar Chart of Cosines A Progressively denser bar charts give way to a simple graph A • f A A f f 1/8/2003 f Inductive Logic 30
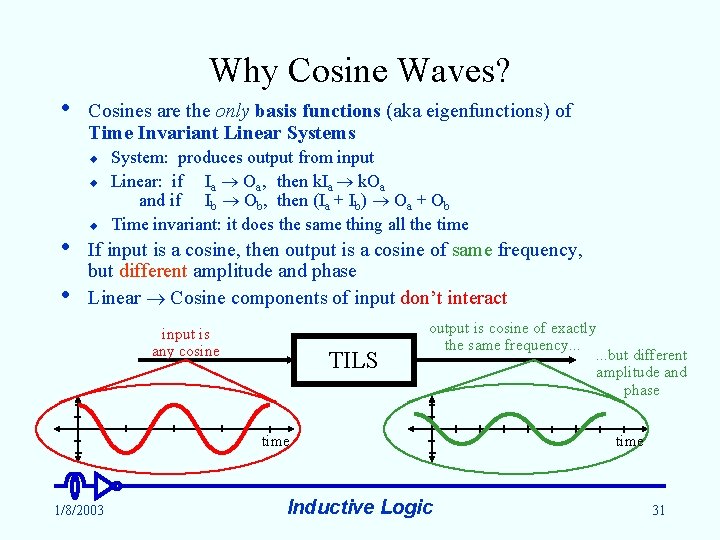
Why Cosine Waves? • Cosines are the only basis functions (aka eigenfunctions) of Time Invariant Linear Systems u u • • u System: produces output from input Linear: if Ia Oa, then k. Ia k. Oa and if Ib Ob, then (Ia + Ib) Oa + Ob Time invariant: it does the same thing all the time If input is a cosine, then output is a cosine of same frequency, but different amplitude and phase Linear Cosine components of input don’t interact input is any cosine TILS output is cosine of exactly the same frequency. . . but different amplitude and phase time 1/8/2003 Inductive Logic time 31
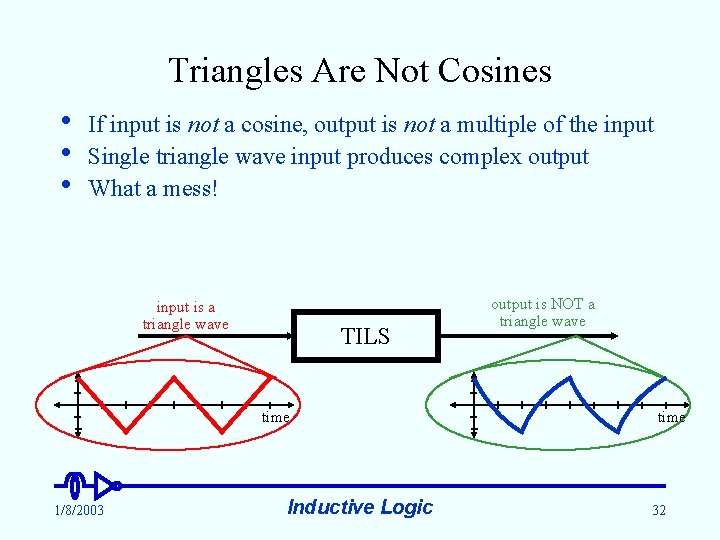
Triangles Are Not Cosines • • • If input is not a cosine, output is not a multiple of the input Single triangle wave input produces complex output What a mess! input is a triangle wave TILS time 1/8/2003 Inductive Logic output is NOT a triangle wave time 32
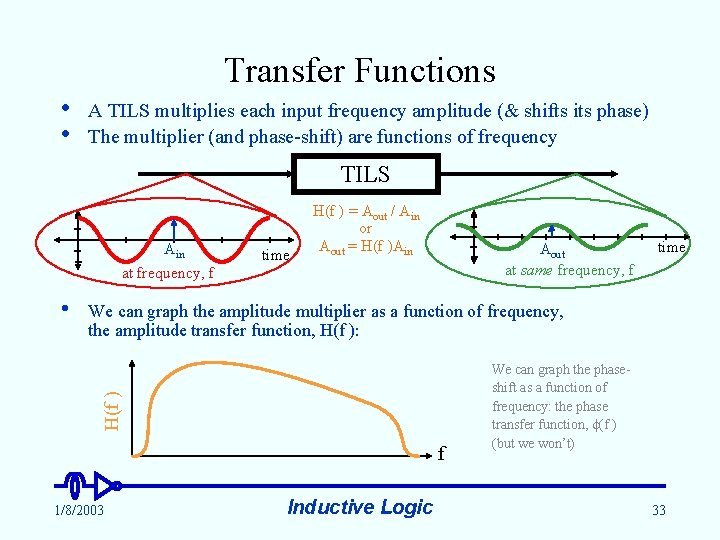
Transfer Functions • • A TILS multiplies each input frequency amplitude (& shifts its phase) The multiplier (and phase-shift) are functions of frequency TILS Ain at frequency, f Aout at same frequency, f time We can graph the amplitude multiplier as a function of frequency, the amplitude transfer function, H(f ): H(f ) • time H(f ) = Aout / Ain or Aout = H(f )Ain f 1/8/2003 Inductive Logic We can graph the phaseshift as a function of frequency: the phase transfer function, (f ) (but we won’t) 33
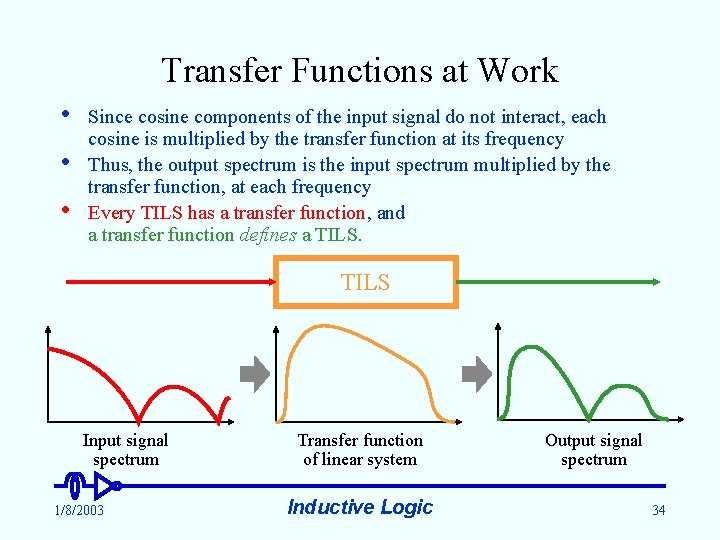
Transfer Functions at Work • • • Since cosine components of the input signal do not interact, each cosine is multiplied by the transfer function at its frequency Thus, the output spectrum is the input spectrum multiplied by the transfer function, at each frequency Every TILS has a transfer function, and a transfer function defines a TILS Input signal spectrum 1/8/2003 Transfer function of linear system Inductive Logic Output signal spectrum 34
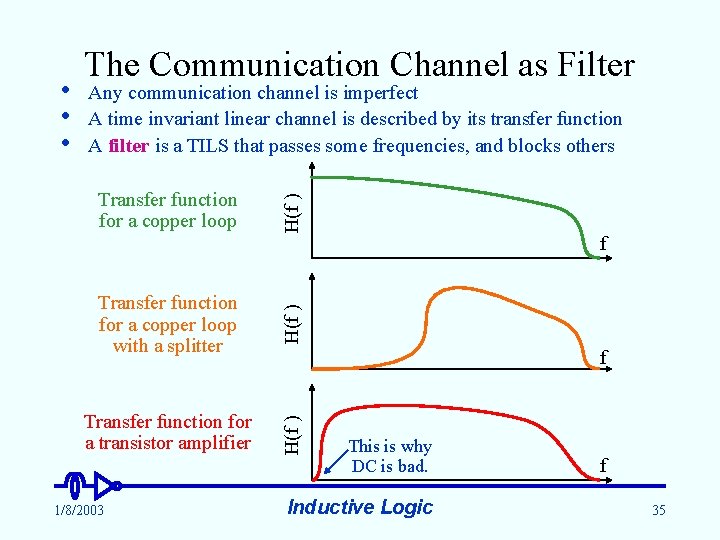
Any communication channel is imperfect A time invariant linear channel is described by its transfer function A filter is a TILS that passes some frequencies, and blocks others Transfer function for a copper loop with a splitter H(f ) Transfer function for a transistor amplifier H(f ) Transfer function for a copper loop H(f ) • • • The Communication Channel as Filter 1/8/2003 f f This is why DC is bad. Inductive Logic f 35
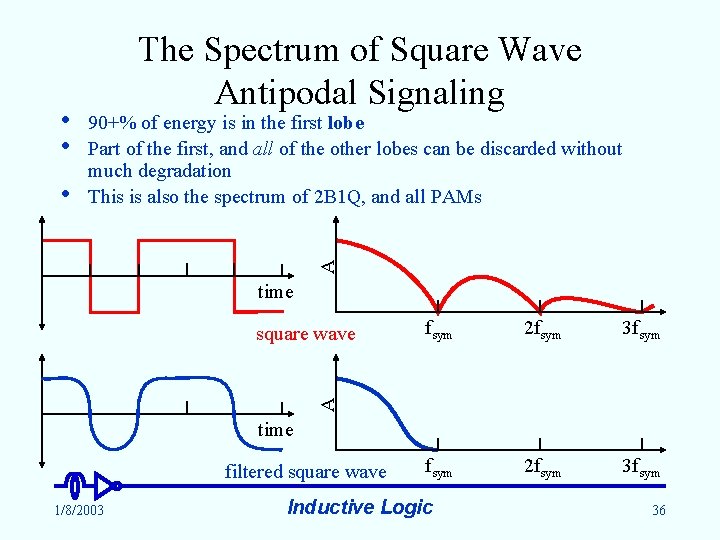
• • 90+% of energy is in the first lobe Part of the first, and all of the other lobes can be discarded without much degradation This is also the spectrum of 2 B 1 Q, and all PAMs A • The Spectrum of Square Wave Antipodal Signaling time fsym 2 fsym 3 fsym A square wave time filtered square wave 1/8/2003 Inductive Logic 36
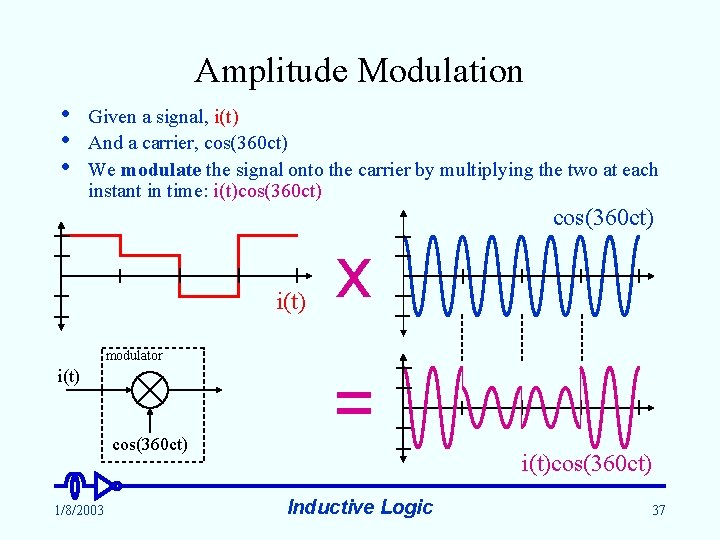
Amplitude Modulation • • • Given a signal, i(t) And a carrier, cos(360 ct) We modulate the signal onto the carrier by multiplying the two at each instant in time: i(t)cos(360 ct) i(t) x modulator i(t) cos(360 ct) 1/8/2003 = i(t)cos(360 ct) Inductive Logic 37

Know Your Identity 1. cos(-a) = cos(a) 2. cos(90 -a) = -cos(90 +a) 3. cos(a+b) = cos(a)cos(b) - cos(90 -a)cos(90 -b) cos(a - b) + cos(a + b) 4. cos(a)cos(b) = cos(90 -a)cos(90 -b) 2 90 -b Demonstration of identity #3 H a H • cos(a) 1/8/2003 cos(90 -a) b 1 u nit Recall that for any right triangle: 90 -a (a os ) c a b cos(a+b) cos(a)cos(b) Inductive Logic cos(90 -a)cos(90 -b) 38
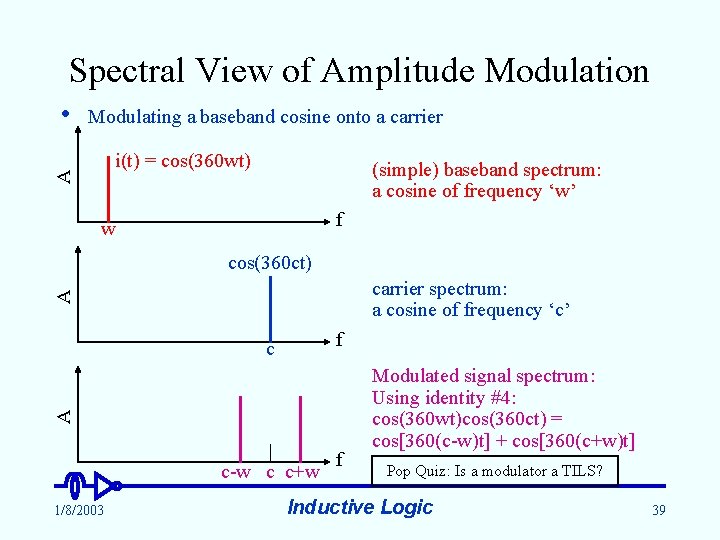
Spectral View of Amplitude Modulation Modulating a baseband cosine onto a carrier i(t) = cos(360 wt) A • (simple) baseband spectrum: a cosine of frequency ‘w’ f w cos(360 ct) A carrier spectrum: a cosine of frequency ‘c’ f A c c-w c c+w 1/8/2003 f Modulated signal spectrum: Using identity #4: cos(360 wt)cos(360 ct) = cos[360(c-w)t] + cos[360(c+w)t] Pop Quiz: Is a modulator a TILS? Inductive Logic 39
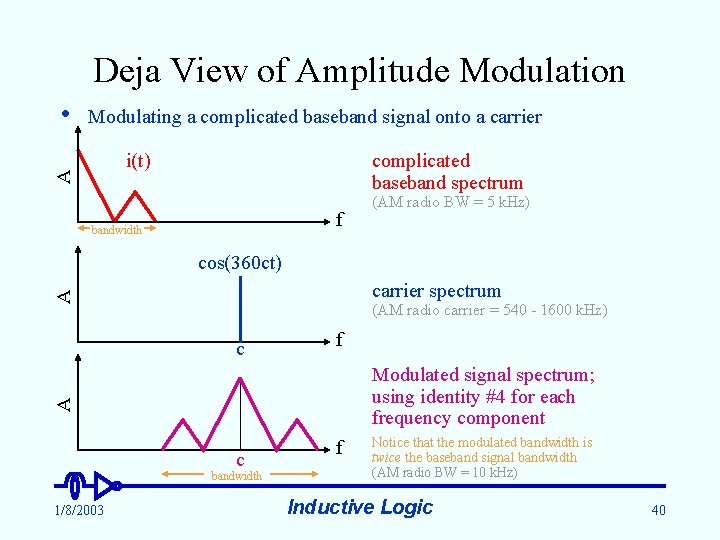
Deja View of Amplitude Modulation Modulating a complicated baseband signal onto a carrier complicated baseband spectrum i(t) A • f bandwidth (AM radio BW = 5 k. Hz) cos(360 ct) A carrier spectrum (AM radio carrier = 540 - 1600 k. Hz) c f A Modulated signal spectrum; using identity #4 for each frequency component c bandwidth 1/8/2003 f Notice that the modulated bandwidth is twice the baseband signal bandwidth (AM radio BW = 10 k. Hz) Inductive Logic 40
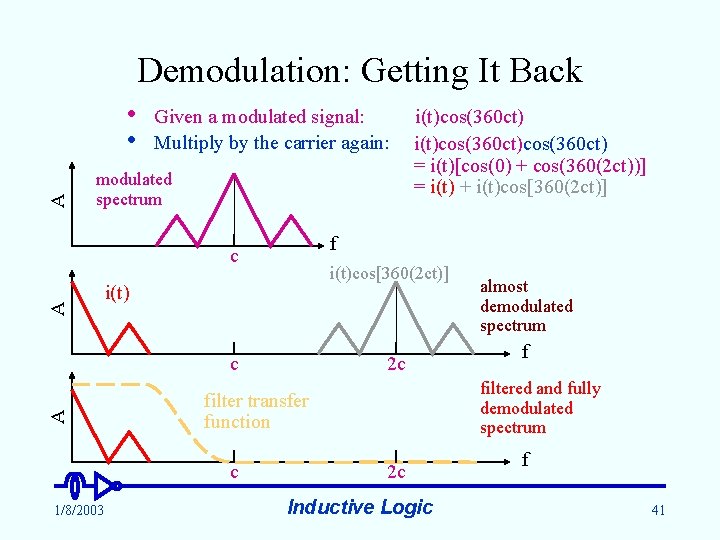
Demodulation: Getting It Back A • • Given a modulated signal: Multiply by the carrier again: modulated spectrum f A c i(t)cos[360(2 ct)] i(t) A c 2 c almost demodulated spectrum f filtered and fully demodulated spectrum filter transfer function c 1/8/2003 i(t)cos(360 ct)cos(360 ct) = i(t)[cos(0) + cos(360(2 ct))] = i(t) + i(t)cos[360(2 ct)] 2 c Inductive Logic f 41
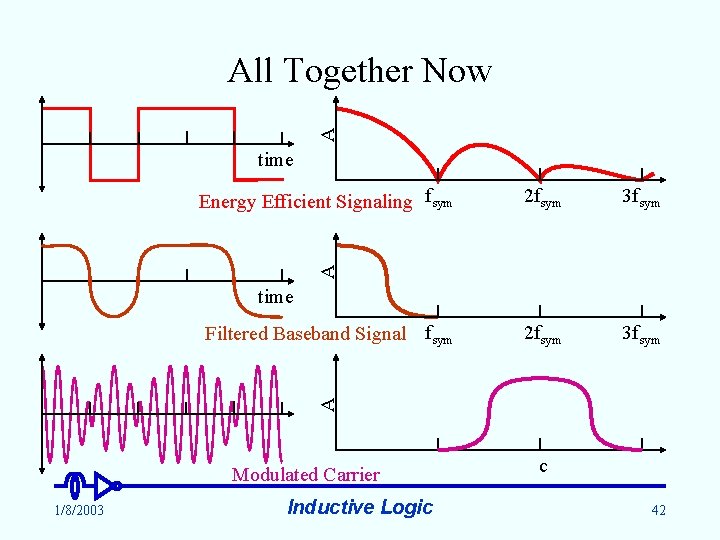
A All Together Now time 2 fsym 3 fsym A Energy Efficient Signaling fsym time A Filtered Baseband Signal fsym Modulated Carrier 1/8/2003 Inductive Logic c 42
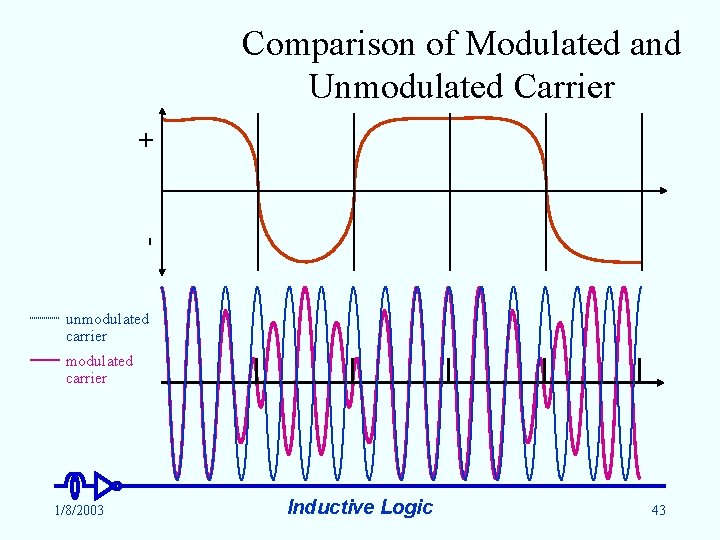
- + Comparison of Modulated and Unmodulated Carrier unmodulated carrier 1/8/2003 Inductive Logic 43

A • Quadrature Multiplexing: Two for the Bandwidth of One Consider a signal modulated with the wrong carrier phase, off by 90. We attempt to demodulate (recall identity #4): i(t)cos(360 ct + 90)cos(360 ct) modulated = i(t)[cos(90) + cos(360(2 ct) + 90)] spectrum = i(t)cos[360(2 ct) + 90] f c A i(t)cos[360(2 ct) + 90] A c 2 c filter transfer function attempted demodulated spectrum f filtered signal spectrum f 1/8/2003 Inductive Logic 44

Quadrature Multiplexing: Part Deux Consider two signals, i(t) and q(t), modulated with two carriers of the same frequency, but different by 90 : i(t)cos(360 ct) + q(t)cos(360 ct + 90) q(t) A i(t) A • baseband spectra f f A modulated signal spectrum: generally not symmetric c 1/8/2003 Inductive Logic f 45
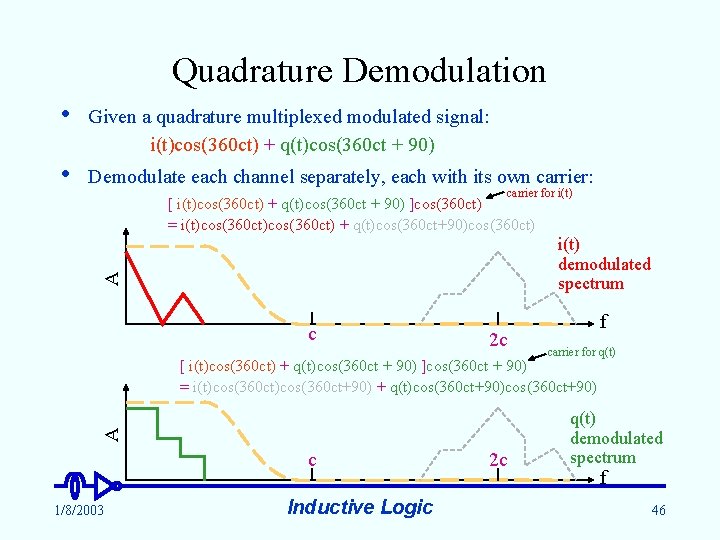
Quadrature Demodulation • Given a quadrature multiplexed modulated signal: i(t)cos(360 ct) + q(t)cos(360 ct + 90) • Demodulate each channel separately, each with its own carrier: carrier for i(t) [ i(t)cos(360 ct) + q(t)cos(360 ct + 90) ]cos(360 ct) = i(t)cos(360 ct) + q(t)cos(360 ct+90)cos(360 ct) A i(t) demodulated spectrum c 2 c f carrier for q(t) A [ i(t)cos(360 ct) + q(t)cos(360 ct + 90) ]cos(360 ct + 90) = i(t)cos(360 ct+90) + q(t)cos(360 ct+90) c 1/8/2003 Inductive Logic 2 c q(t) demodulated spectrum f 46

DMT ADSL • • Discrete Multi-Tone Up to 255 “separate” carriers, u u • u Each carrier is quadrature multiplexed multi-level PAM Two to 15 bits per symbol per carrier (2 - 256 PAM per I/Q axis) Optimum filling of data into the carriers for maximum total SNR All share the same time, frequency, and phase references Lower carriers omitted for baseband voice Carrier spacing is 4312. 5 Hz A upstream downstream baseband voice 300 Hz 1/8/2003 3600 Hz N x 4312. 5 Hz Inductive Logic f 47
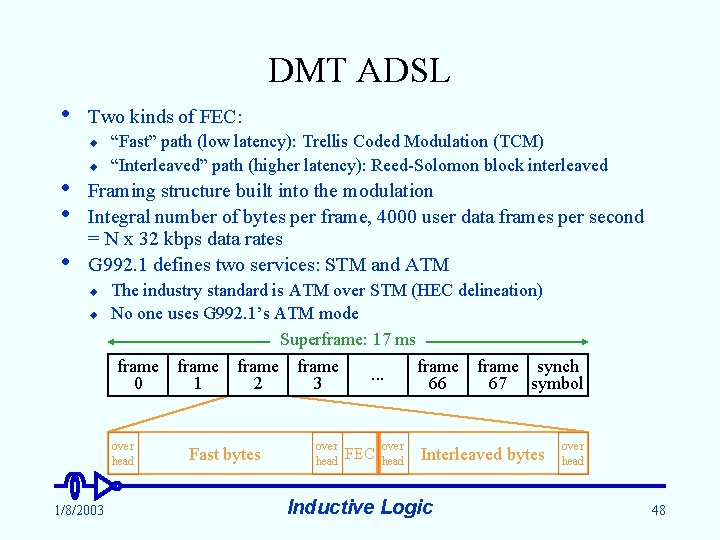
DMT ADSL • Two kinds of FEC: u • • • u “Fast” path (low latency): Trellis Coded Modulation (TCM) “Interleaved” path (higher latency): Reed-Solomon block interleaved Framing structure built into the modulation Integral number of bytes per frame, 4000 user data frames per second = N x 32 kbps data rates G 992. 1 defines two services: STM and ATM u u The industry standard is ATM over STM (HEC delineation) No one uses G 992. 1’s ATM mode Superframe: 17 ms frame frame synch. . . 0 1 2 3 66 67 symbol over head 1/8/2003 Fast bytes over head FEC over head Interleaved bytes Inductive Logic over head 48
- Slides: 48