BARISAN DERET LIA INDRIANI A 410080057 barisan Geometri

BARISAN DERET LIA INDRIANI A 410080057

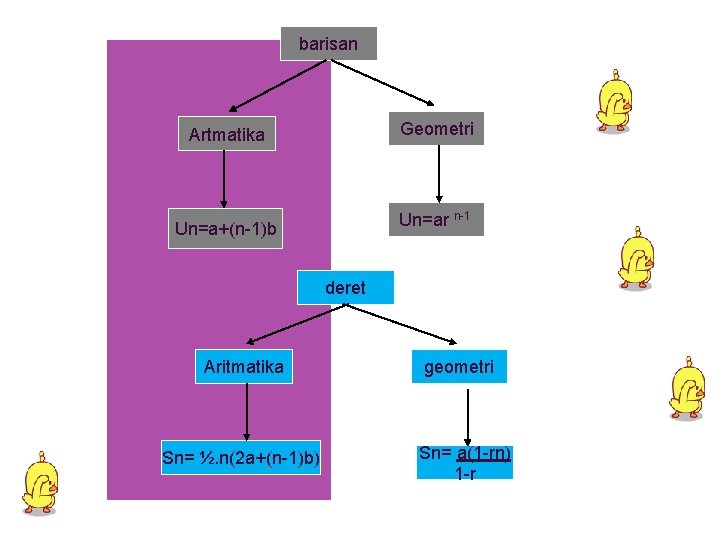
barisan Geometri Artmatika Un=ar n-1 Un=a+(n-1)b deret Aritmatika Sn= ½. n(2 a+(n-1)b) geometri Sn= a(1 -rn) 1 -r

A. Barisan Aritmatika

Barisan aritmatika adalah barisan bilangan dimana selisih dua suku yang berurutan selalu tetap besarnya. Nilai yang tetap tersebut disebut beda, disimbolkan dengan b. U 1, U 2, U 3. . . Un Barisan aritmatika U 2 -U 1=U 3 -U 2=. . . =tetap=beda b=Un-Un-1

Rumus suku ke-n = Un Bentuk umum barisan aritmatika Un=suku ke-n a= suku pertama b= beda Un=a+(n-1)b a+(a+b)+(a+2 b)+(a+3 b)+. . . U 1 = a U 2=a+b U 3=a+2 b Un=a+(n-1)b

C 0 ntoh: Diketahui barisan bilangan 2, 5, 8, . . . Hitunglah suku ke 50 (U 50)! Jawab: U 1 = a = 2 b = U 2 -U 1 = 3 n = 50 Un = a + (n-1)b U 50 = 2+(50 -1)3 = 149

B. DERET ARITMATIKA

Perhatikan deret aritmatika a+(a+b)+(a+2 b)+. . . Jika jumlah n suku pertama dinyatakan dengan Sn, maka: Sn = a+(a+b)+(a+2 b)+. . . Un Sn = Un+. . . +(a+2 b)+(a+b)+a 2 Sn = (a+Un)+(a+Un)+. . . +(a+Un) 2 Sn = n. (a+Un) Sn = 1/2 n(a+Un) Atau Sn = 1/2 n{a+a+(n-1)b} Sn = ½ n {2 a+(n-1)b} = ½ n {2 a+{n-1}b} Sn = ½ n {2 a+{n-1}b}

Contoh : suatu deret aritmatika diketahui 12+15+18+. . . , hitung S 10! Jawab: a =12, b= 3, n= 10 Un =a+(n-1)b U 10 = 12+(10 -1)3 =39 Sn = 1/2 n(a+Un) S 10 = ½. 10(12+39) =255

Soal 1. Diketahui barisan aritmatika U 7 = 19 dan U 13 = 37, hitunglah U 20! 2. Dalam suatu barisan aritmatika diketahui suku ke-n adalah 9 sedanngkan jumlah suku ke-5 dan ke-7 adalah 36. tentukan suku ke 100 barisan tersebut! 3. Tentukan jumlah 20 suku pertama dari deret aritmatika : 3+7+11+. . . !

TERIMAKASIH