Baris Deret Penerapan Ekonomi Matematika Ekonomi Model Perkembangan

Baris & Deret : Penerapan Ekonomi Matematika Ekonomi

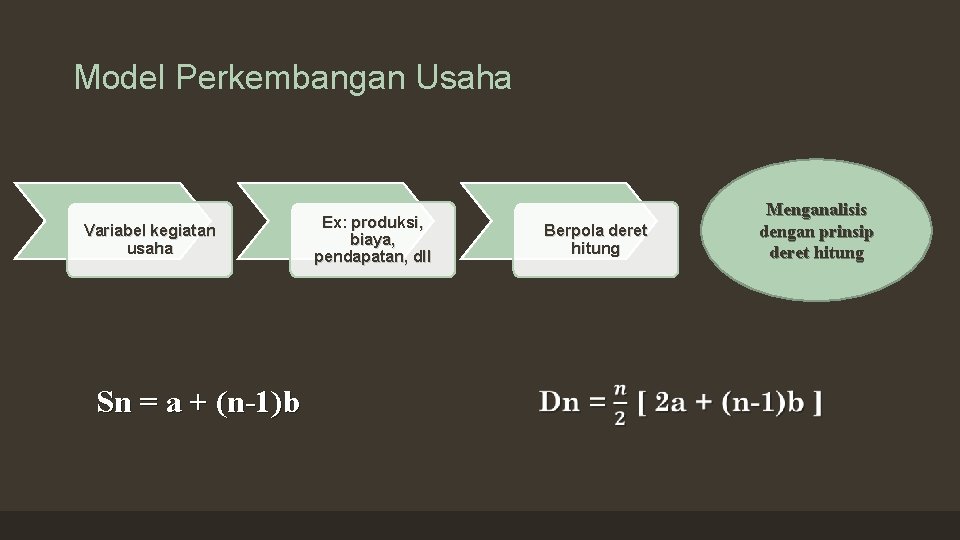
Model Perkembangan Usaha Variabel kegiatan usaha Sn = a + (n-1)b Ex: produksi, biaya, pendapatan, dll Berpola deret hitung Menganalisis dengan prinsip deret hitung

Contoh 1 1. Perusahaan kursi “Maju Mundur” menghasilkan 3. 000 kursi pada bulan pertama produksinya. Dengan menambah tenaga kerja dan peningkatan produksivitasnya, perusahaan mampu menambah produksi sebanyak 500 kursi setiap bulannya. Jika perkembangan produksinya konstan, berapa kursi yang di hasilkan pada bulan kelima? Berapa kursi yang telah dihasilkan sampai bulan kelima?

Jawab: Diketahui: a = 3. 000 b = 500 n=5 Ditanya: S 5 dan D 5 ? •

Contoh 2 2. Besarnya penerimaan PT Merpati dari hasil penjualan barangnya 720 juta rupiah pada tahun kelima dan 980 juta rupiah pada tahun ketujuh. Apabila perkembangan penerimaan penjualan tersebut berpola seperti deret hitung, berapa perkembangan penerimaannya per tahun? Berapa besar penerimaan pada tahun pertama dan pada tahun berapa penerimaannya mencapai 460 juta rupiah?

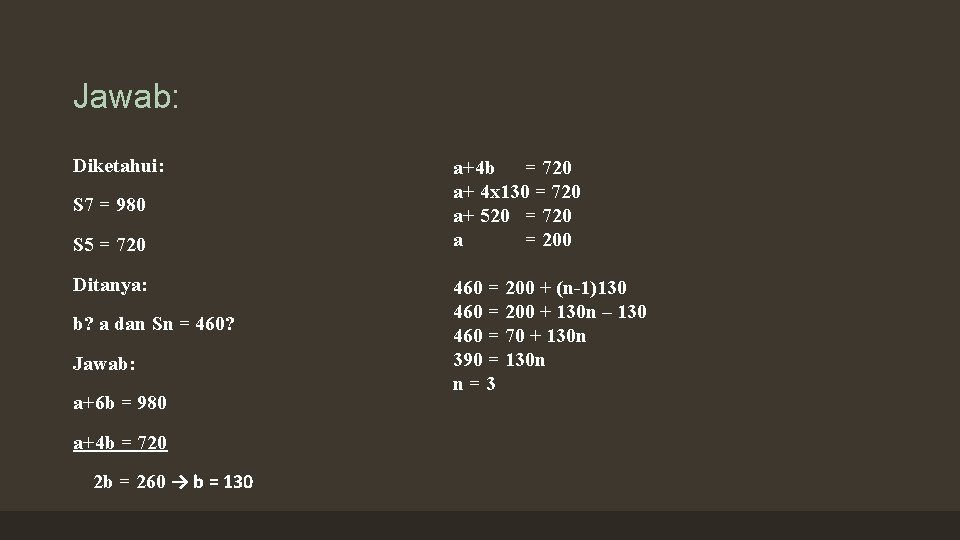
Jawab: Diketahui: S 7 = 980 S 5 = 720 Ditanya: b? a dan Sn = 460? Jawab: a+6 b = 980 a+4 b = 720 2 b = 260 → b = 130 a+4 b = 720 a+ 4 x 130 = 720 a+ 520 = 720 a = 200 460 = 200 + (n-1)130 460 = 200 + 130 n – 130 460 = 70 + 130 n 390 = 130 n n=3

Model Pertumbuhan Penduduk Pt = P 1 x Rt-1 dimana: R = 1 + r Penduduk dunia tumbuh mengikuti pola deret ukur P 1 : jumlah pada tahun pertama (basis) Pi : jumlah pada tahun ke-t r : persentase pertumbuhan per tahun t : indeks waktu (tahun)

Contoh 1 1. Penduduk kota A berjumlah 1 juta jiwa pada tahun 1991, tingkat pertumbuhannya 4% per tahun. Hitunglah jumlah penduduk kota tersebut pada tahun 2006. Jika mulai tahun 2006 pertumbuhannya menurun menjadi 2, 5%, berapa jumlahnya pada 11 tahun kemudian?

Jawab Diketahui: P 1 = 1. 000 P 1 = 1. 800. 943 r = 4% atau 0, 04 r = 2, 5% atau 0, 025 R = 1 + 0, 04 = 1, 04 R = 1 + 0, 025 = 1, 025 Ditanya: P 16? Ditanya: P 11? Jawab: P 16 = 1. 000 x (1, 04)16 -1 P 11 = 1. 800. 943 x (1, 025)11 -1 P 16 = 1. 800. 943 P 11 = 2. 305. 359

Teori Nilai Uang (Bunga Majemuk) •

Contoh 1 1. Amir meminjam uang di bank sebanyak 5 juta rupiah untuk jangka waktu 3 tahun, dengan tingkat bunga 2%/th. Berapa jumlah seluruh uang yang harus dikembalikannya saat pelunasan? Seandainya perhitungan pembayaran bunga menjadi setiap semester, berapa jumlah yang harus dia kembalikan?

Jawab: Diketahui: P = 5. 000 n = 3 i = 2% atau 0, 02 Ditanya: F 3? Jawab: F 3 = 5. 000 (1+0, 02)3 F 3 = 5. 306. 040 •

Contoh 2 2. Daniel memiliki tabungan yang pada tiga tahun mendatang akan berjumlah Rp 532. 400, - Jika tingkat bunga yang berlaku 10%/th, berapa tabungan Daniel pada saat sekarang?

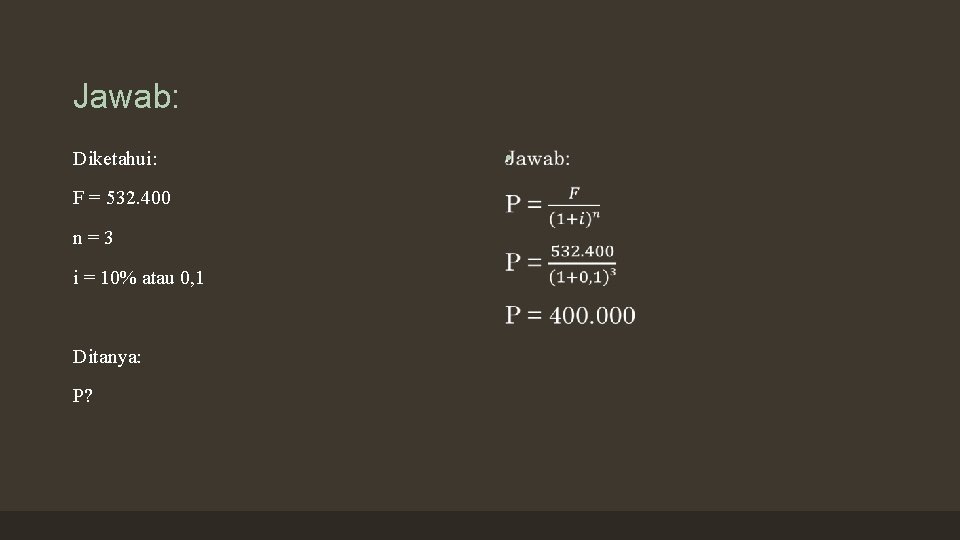
Jawab: Diketahui: F = 532. 400 n = 3 i = 10% atau 0, 1 Ditanya: P? •

Terima kasih Selamat belajar