Bankers Algorithm Example of Bankers Algorithm 5 processes

Bankers Algorithm

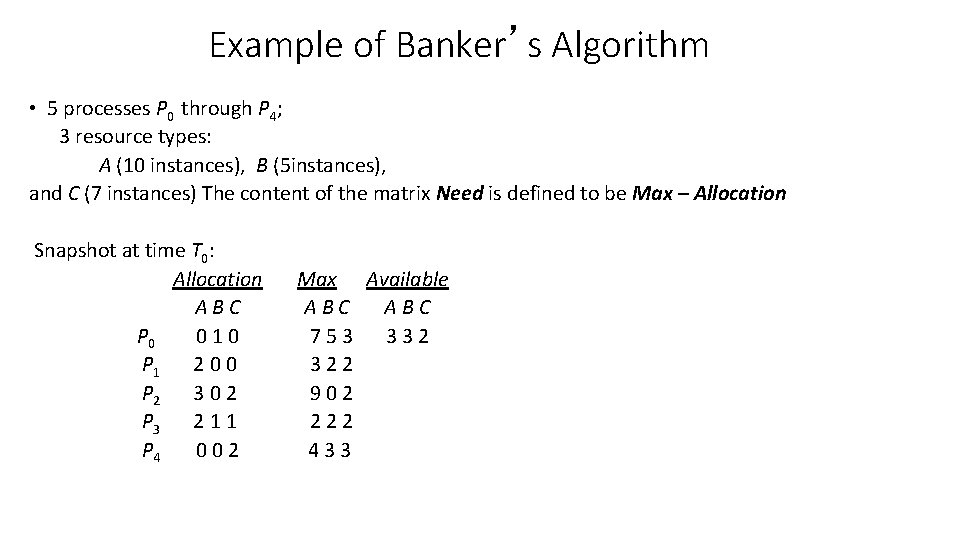
Example of Banker’s Algorithm • 5 processes P 0 through P 4; 3 resource types: A (10 instances), B (5 instances), and C (7 instances) The content of the matrix Need is defined to be Max – Allocation Snapshot at time T 0: Allocation ABC P 0 010 P 1 2 0 0 P 2 3 0 2 P 3 2 1 1 P 4 002 Max Available ABC 753 332 322 902 222 433

Q 1: Is the system in a safe state ? / The system is in a safe state since the sequence < P 1, P 3, P 4, P 0, P 2> satisfies safety criteria Q 2: Can request for (3, 3, 0) by P 2 be granted?

NEED = MAX – ALLOCATION Available[n] = Available[n-1]+Allocation[n]

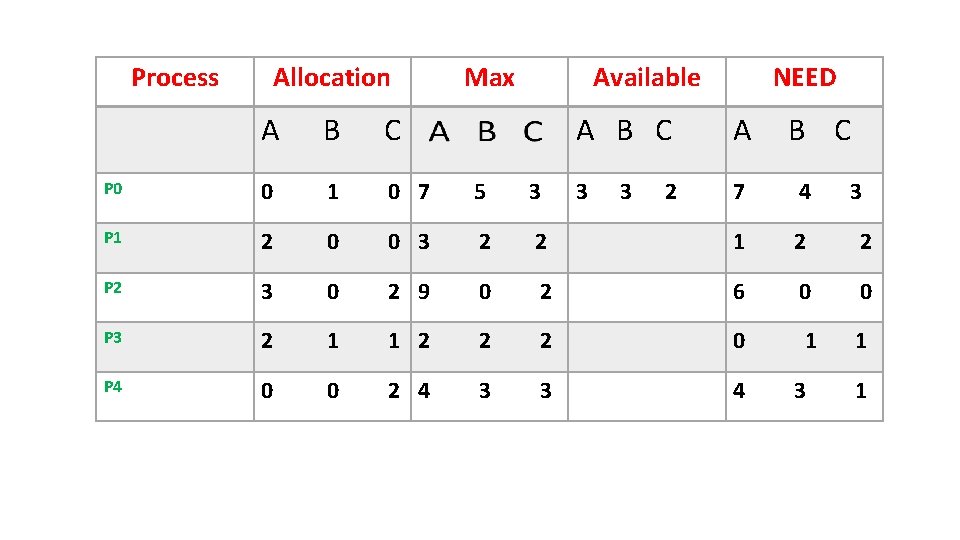
Process Allocation Max Available A B C P 0 0 1 0 7 5 3 P 1 2 0 0 3 2 P 2 3 0 2 9 P 3 2 1 P 4 0 0 NEED A B C A 3 7 4 2 1 2 2 0 2 6 0 0 1 2 2 2 0 1 1 2 4 3 3 4 3 2 B C 3 3 1

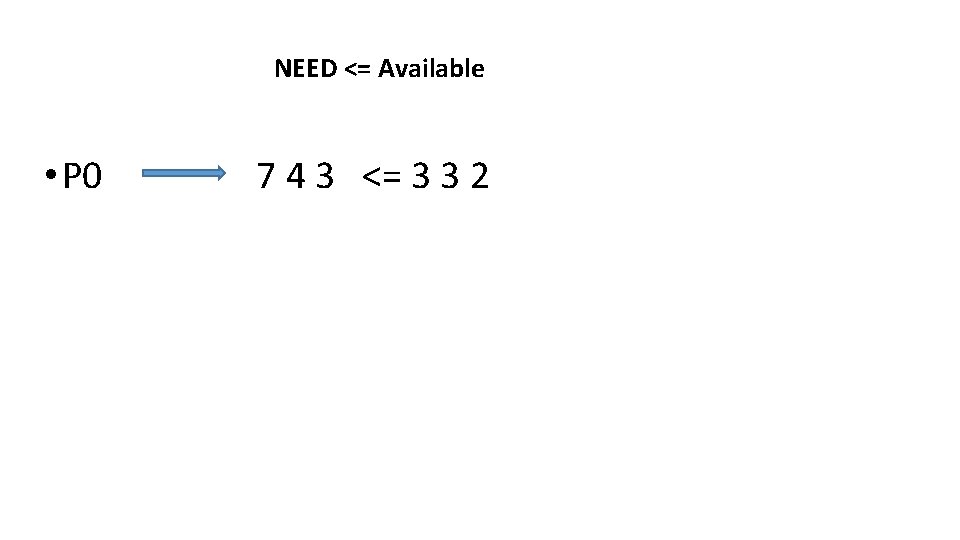
NEED <= Available • P 0 7 4 3 <= 3 3 2

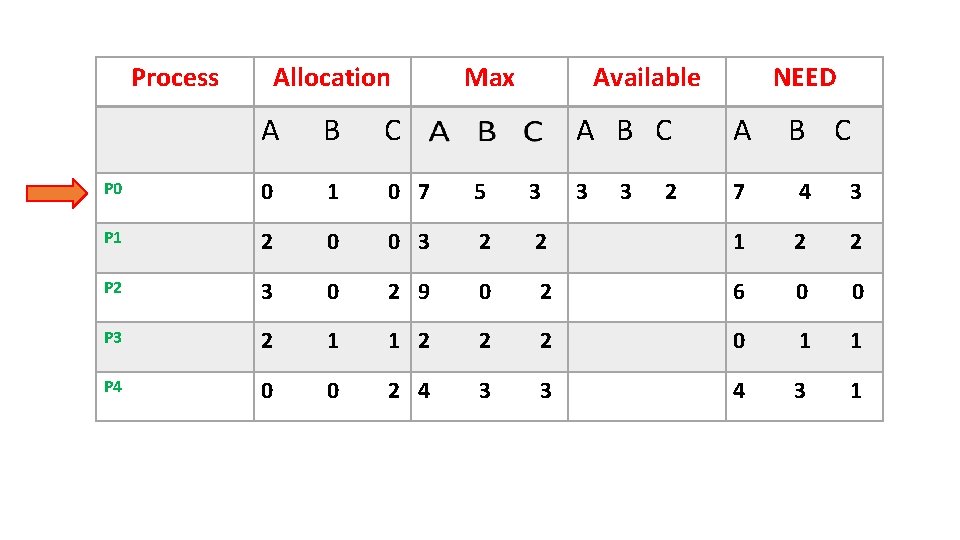
Process Allocation Max Available A B C P 0 0 1 0 7 5 3 P 1 2 0 0 3 2 P 2 3 0 2 9 P 3 2 1 P 4 0 0 NEED A B C A 3 7 4 3 2 1 2 2 0 2 6 0 0 1 2 2 2 0 1 1 2 4 3 3 4 3 1 3 2 B C

• P 1 1 2 2 <= 3 3 2 Available= Available + Allocation =332 +200 =5 3 2

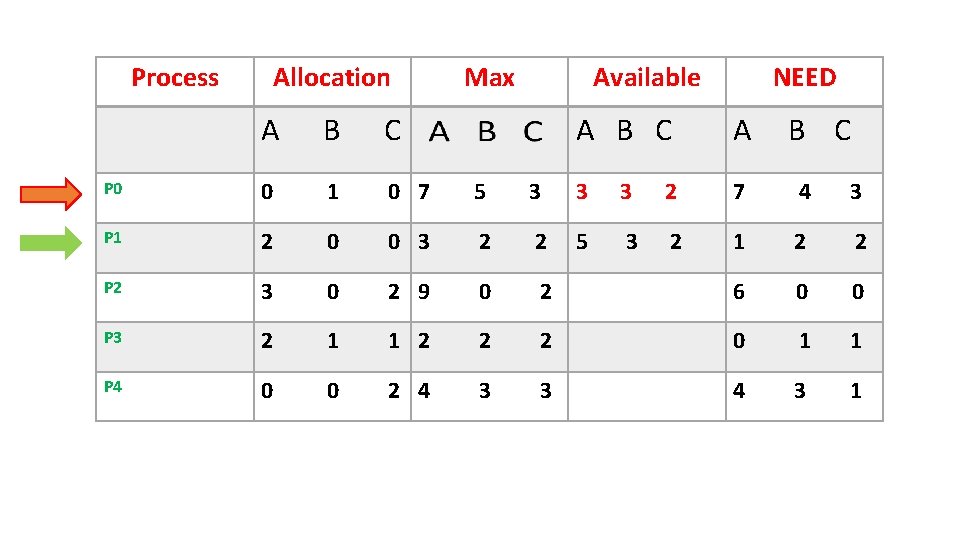
Process Allocation Max A B C P 0 0 1 0 7 5 P 1 2 0 0 3 P 2 3 0 P 3 2 P 4 0 Available NEED A B C 3 3 3 2 7 4 3 2 2 5 3 2 1 2 2 2 9 0 2 6 0 0 1 1 2 2 2 0 1 1 0 2 4 3 3 4 3 1

P 2 6 0 0 <= 5 3 2 P 3 0 1 1 <= 5 3 2 Available[n]= Available + Allocation =532 +211 =7 4 3

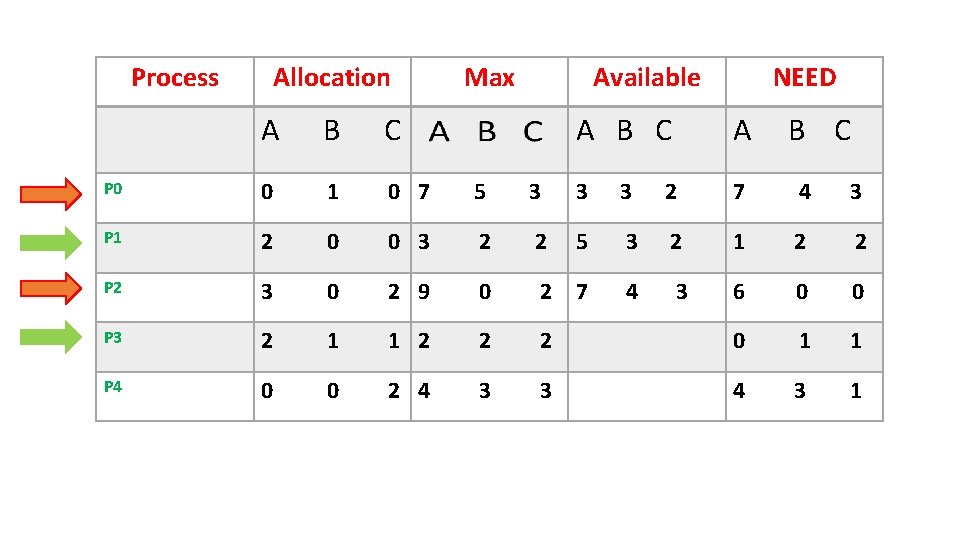
Process Allocation Max A B C P 0 0 1 0 7 5 P 1 2 0 0 3 P 2 3 0 P 3 2 P 4 0 Available NEED A B C 3 3 3 2 7 4 3 2 2 5 3 2 1 2 2 2 9 0 2 7 4 3 6 0 0 1 1 2 2 2 0 1 1 0 2 4 3 3 4 3 1

P 4 4 3 1 <= 5 3 2 Available[n]= Available + Allocation =7 4 3+002 =745

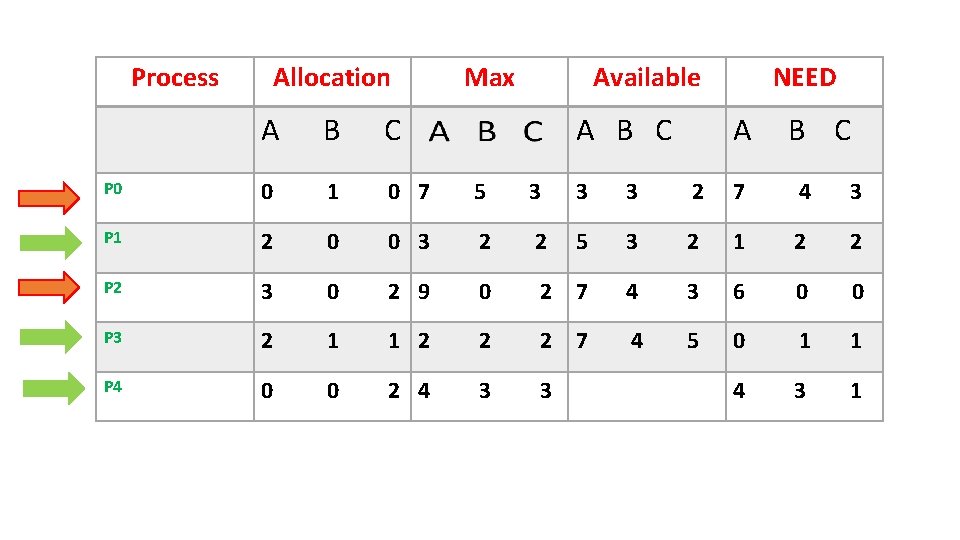
Process Allocation Max Available A B C NEED A B C P 0 0 1 0 7 5 3 3 3 2 7 4 3 P 1 2 0 0 3 2 2 5 3 2 1 2 2 P 2 3 0 2 9 0 2 7 4 3 6 0 0 P 3 2 1 1 2 2 2 7 4 5 0 1 1 P 4 0 0 2 4 3 3 4 3 1

P 0 7 4 3 <= 7 4 5 Available[n]= Available + Allocation =745 +010 =7 5 5

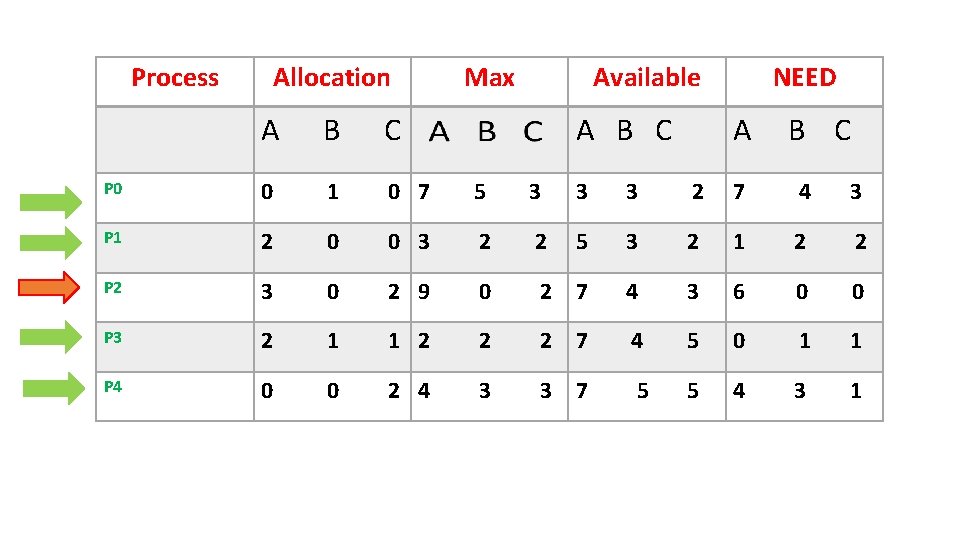
Process Allocation Max Available A B C NEED A B C P 0 0 1 0 7 5 3 3 3 2 7 4 3 P 1 2 0 0 3 2 2 5 3 2 1 2 2 P 2 3 0 2 9 0 2 7 4 3 6 0 0 P 3 2 1 1 2 2 2 7 4 5 0 1 1 P 4 0 0 2 4 3 3 7 5 5 4 3 1

P 2 6 0 0 <= 7 5 5 Available[n]= Available + Allocation =755 +302 = 10 5 7

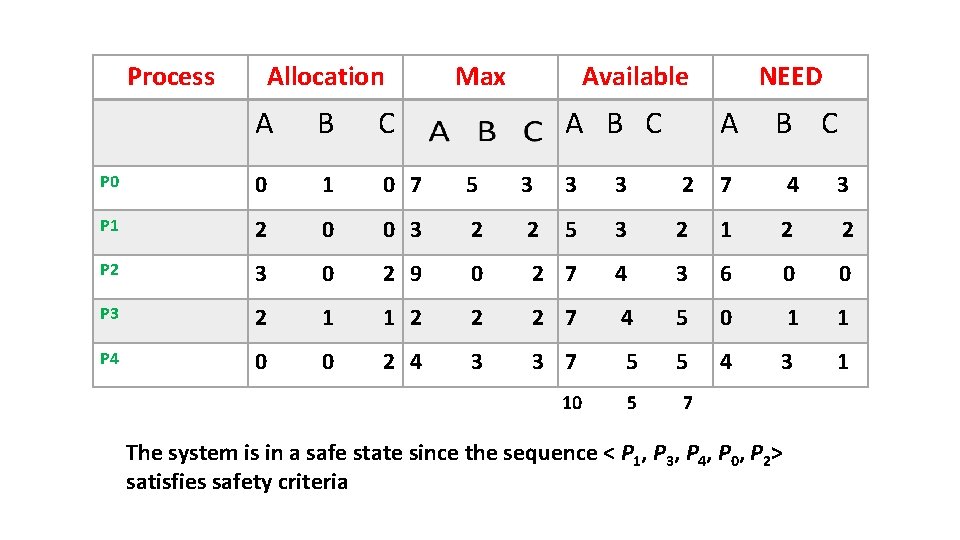
Process Allocation Max Available A B C NEED A B C P 0 0 1 0 7 5 3 3 3 2 7 4 3 P 1 2 0 0 3 2 2 5 3 2 1 2 2 P 2 3 0 2 9 0 2 7 4 3 6 0 0 P 3 2 1 1 2 2 2 7 4 5 0 1 1 P 4 0 0 2 4 3 3 7 5 5 4 3 1 10 5 7 The system is in a safe state since the sequence < P 1, P 3, P 4, P 0, P 2> satisfies safety criteria

• The system is in a safe state since the sequence < P 1, P 3, P 4, P 0, P 2> satisfies safety criteria

For, Exercise 02 Q 1: Find Out Need matrix and Is the system in a safe state ?

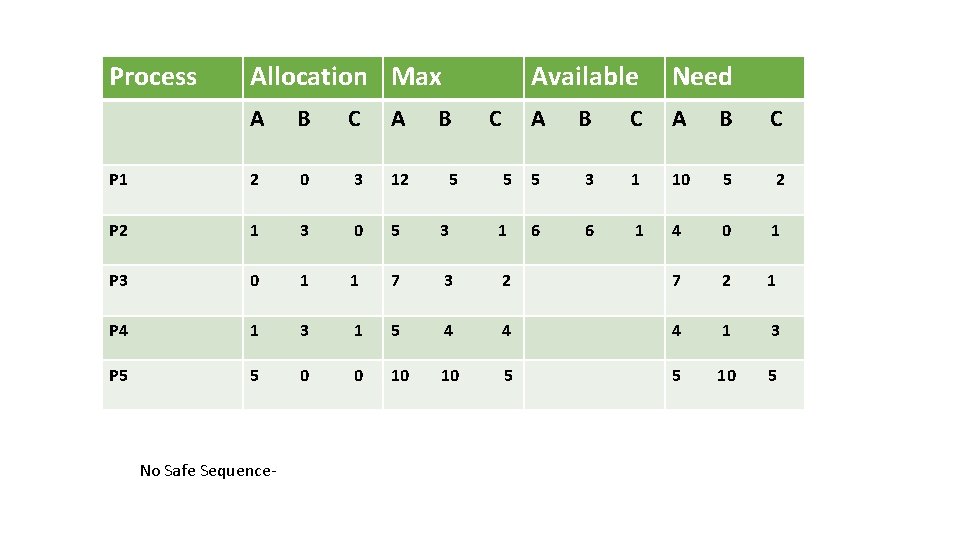
Process Allocation Max Need A B C 5 5 3 1 10 5 2 6 6 1 4 0 1 A B C A P 1 2 0 3 12 P 2 1 3 0 5 3 1 P 3 0 1 1 7 3 2 7 2 1 P 4 1 3 1 5 4 4 4 1 3 P 5 5 0 0 10 10 5 5 10 5 No Safe Sequence- B Available 5 C

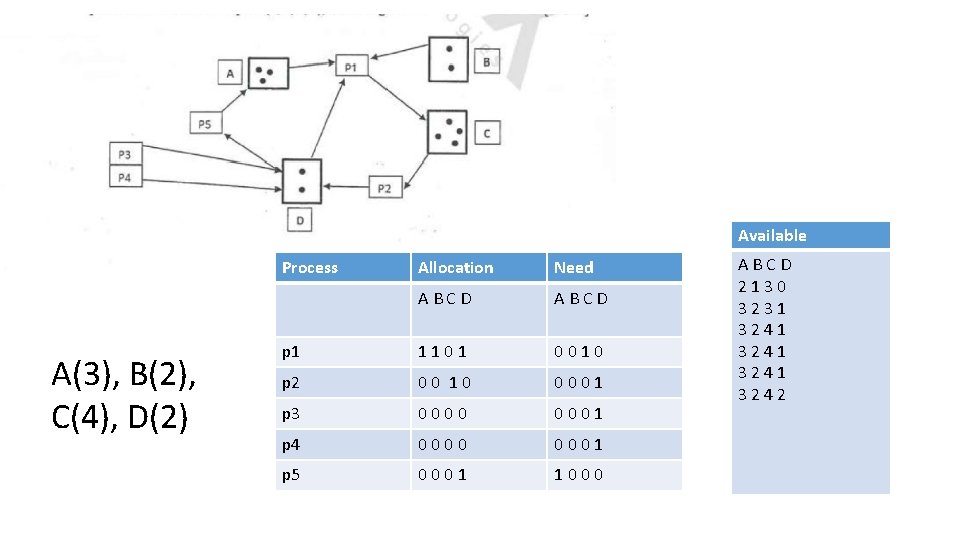
Available Process A(3), B(2), C(4), D(2) Allocation Need ABCD p 1 1101 0010 p 2 00 10 0001 p 3 0000 0001 p 4 0000 0001 p 5 0001 1000 ABCD 2130 3231 3241 3242

Q 2: Can request for (1, 0, 2) by P 1 be immediately granted?

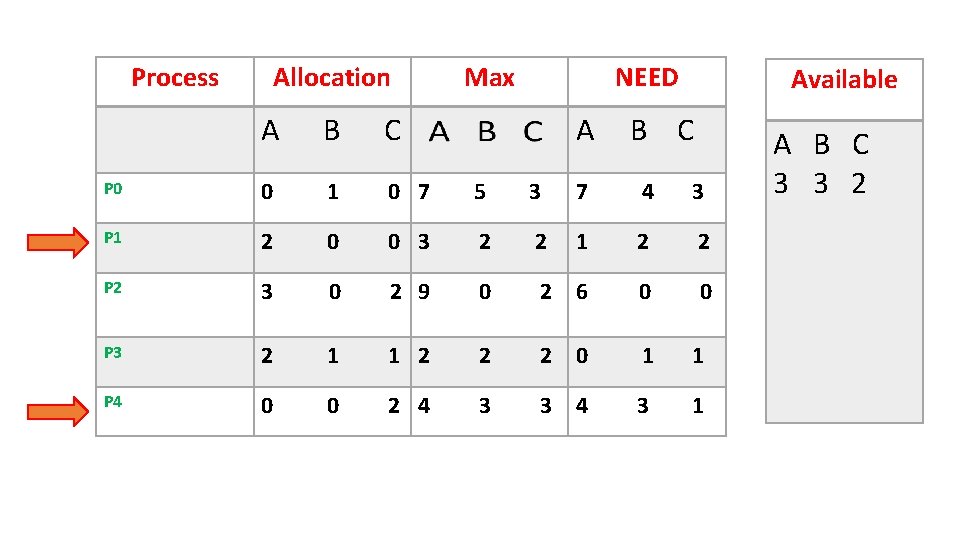
Process Allocation Max NEED A Available A B C P 0 0 1 0 7 5 3 7 4 3 P 1 2 0 0 3 2 2 1 2 2 P 2 3 0 2 9 0 2 6 0 0 P 3 2 1 1 2 2 2 0 1 1 P 4 0 0 2 4 3 3 4 3 1 A B C 3 3 2

If request <= NEED If request <= Available • Available = 3 3 2 – 1 0 2 = 2 3 0 • Allocation= 2 0 0 + 1 0 2 = 3 0 2 • NEED = 1 2 2 – 1 0 2 = 0 2 0

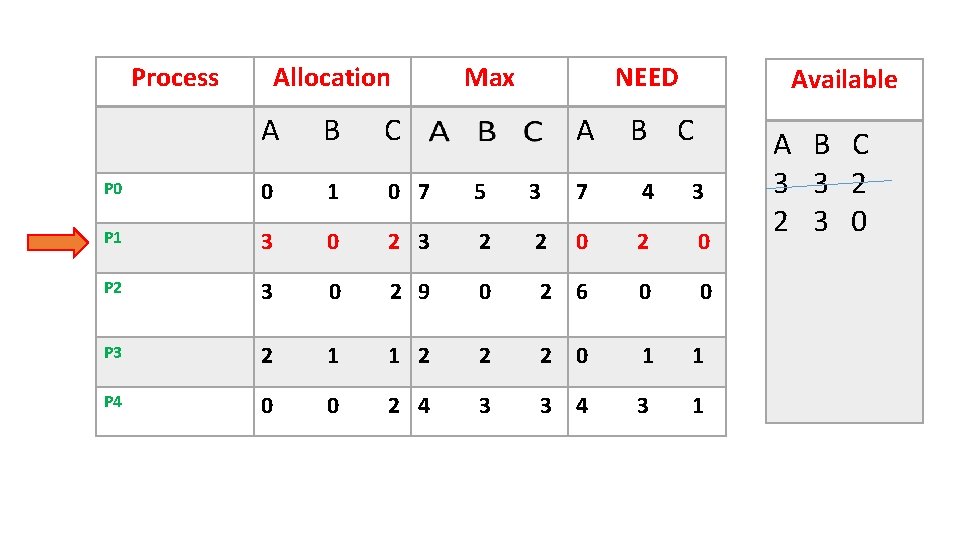
Process Allocation Max NEED A Available A B C P 0 0 1 0 7 5 3 7 4 3 P 1 3 0 2 3 2 2 0 P 2 3 0 2 9 0 2 6 0 0 P 3 2 1 1 2 2 2 0 1 1 P 4 0 0 2 4 3 3 4 3 1 A B C 3 3 2 2 3 0