Ball and plate system Making an unstable system

Ball and plate system Making an unstable system stable J. Gorasia and D. Greeley

Goals • Making an unstable system stable • Make system capable of rejecting noise • Decent transient response

The Plant Proportional Angular Displacement Approximation

Transfer Function Small angle approximation Transfer Function

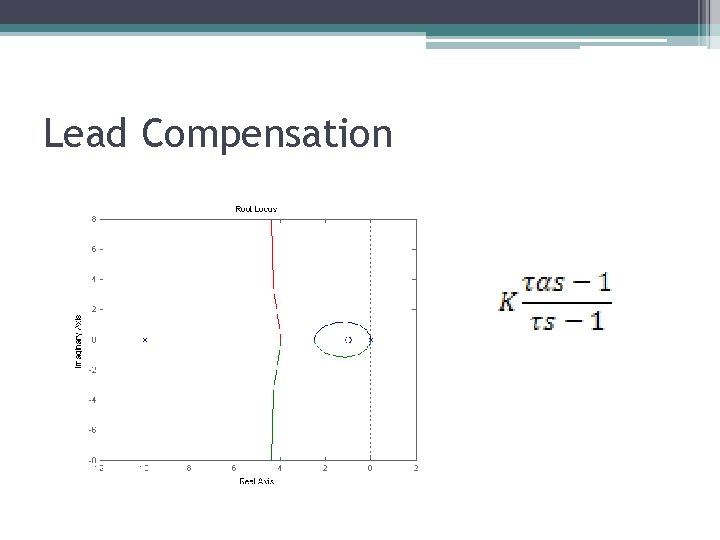
Lead Compensation

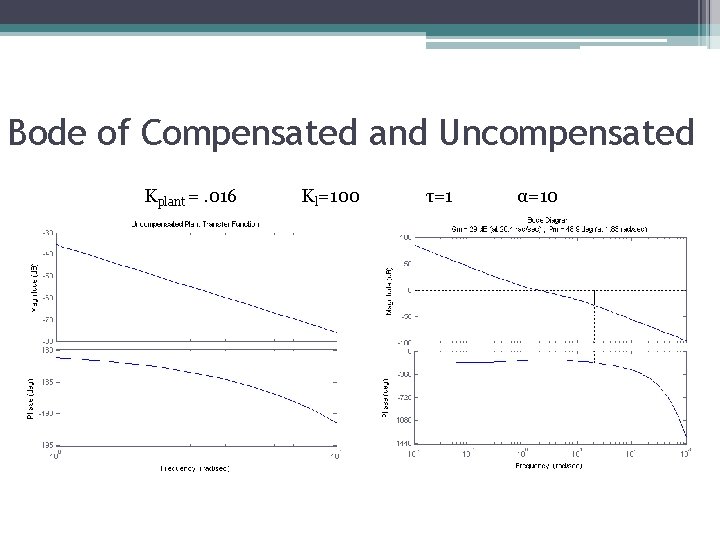
Bode of Compensated and Uncompensated Kplant =. 016 Kl=100 τ=1 α=10

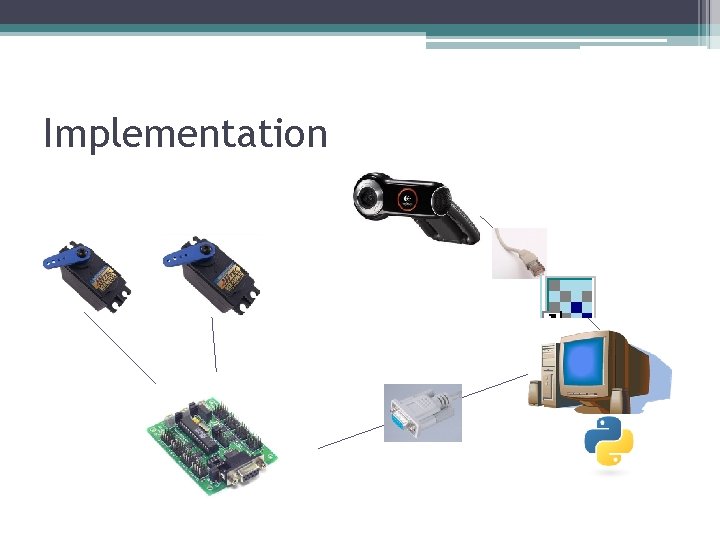
Implementation

Sensors 1. 2. 3. 4. Affine Filter for colors Threshold Find centroid 1 2 3 4 Resolution: 160 x 120 33 frames per second

Motors • Hitec HSR-5995 TG • Moves at maximum speed of 0. 12 sec/60 degrees • Which translates to a maximum frequency of 1. 4 rad/s of the plate • Torque 417 oz-in

Discretization • Use design by emulation ▫ Do everything in s domain, then digitize • Substitute s to z using: • Solve for largest power of the output • Then perform the inverse z transform

Discrete Compensator

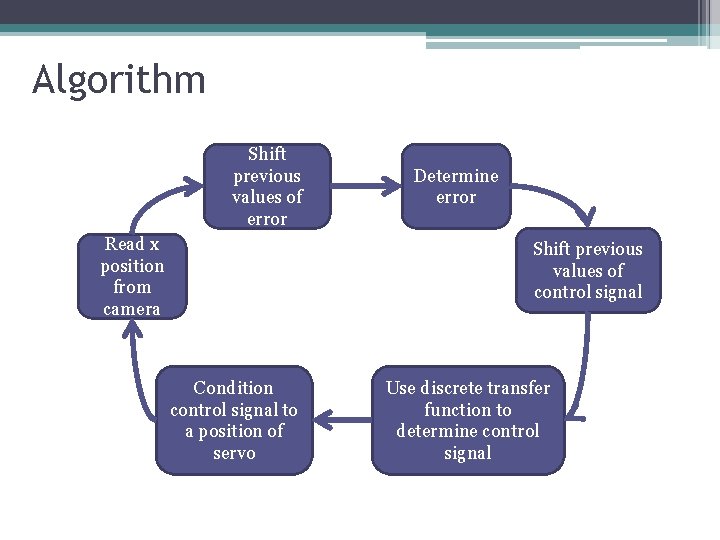
Algorithm Shift previous values of error Read x position from camera Determine error Shift previous values of control signal Condition control signal to a position of servo Use discrete transfer function to determine control signal

Verification • Goals met? • Model accurate? • What are the sources of error? ▫ ▫ ▫ Image tracking Saturation Discrete angle positions Bending of the plate Model of servos

Going forward • • Use vvvv or FPGA for vision tracking More angular displacement of plant Use RTOS or embedded chip for control system Better plant design

Questions?