Balanced Trees Ellen Walker CPSC 201 Data Structures

Balanced Trees Ellen Walker CPSC 201 Data Structures Hiram College

Search Tree Efficiency • The average time to search a binary tree is the average path length from root to leaf • In a tree with N nodes, this is… – Best case: log N (the tree is full) – Worst case: N (the tree has only one path) • Worst case tree examples – Items inserted in order – Items inserted in reverse order

Keeping Trees Balanced • Change the insert algorithm to rebalance the tree • Change the delete algorithm to rebalance the tree • Many different approaches, we’ll look at one – RED-BLACK trees – Based on non-binary trees (2 -3 -4 trees)

2 -3 Trees • Relax constraint that a node has 2 children • Allow 2 -child nodes and 3 -child nodes – With bigger nodes, tree is shorter & branchier – 2 -node is just like before (one item, two children) – 3 -node has two values and 3 children (left, middle, right) < x , y> <=x >x and <=y >y

Why 2 -3 tree • Faster searching? – Actually, no. 2 -3 tree is about as fast as an “equally balanced” binary tree, because you sometimes have to make 2 comparisons to get past a 3 -node • Easier to keep balanced? – Yes, definitely. – Insertion can split 3 -nodes into 2 -nodes, or promote 2 -nodes to 3 -nodes to keep tree approximately balanced!

3 -Node and Equivalent 2 -Nodes 20 10, 20 L M 10 R L 10 R M 20 L M R

Inserting into 2 -3 Tree • As for binary tree, start by searching for the item • If you don’t find it, and you stop at a 2 -node, upgrade the 2 -node to a 3 -node. • If you don’t find it, and you stop at a 3 -node, you can’t just add another value. So, replace the 3 -node by 2 2 -nodes and push the middle value up to the parent node • Repeat recursively until you upgrade a 2 -node or create a new root. • When is a new root created?

Why is this better? • Intuitively, you unbalance a binary tree when you add height to one path significantly more than other possible paths. • With the 2 -3 insert algorithm, you can only add height to the tree when you create a new root, and this adds one unit of height to all paths simultaneously. • Hence, the average path length of the tree stays close to log N.

Deleting from a 2 -3 Tree • Like for a binary tree, we want to start our deletion at a leaf • First, swap the value to be deleted with its immediate successor in the tree (like binary search tree delete) • Next, delete the value from the node. – If the node still has a value, you’ve changed a 3 node into a 2 -node; you’re done – If no value is left, find a value from sibling or parent

Deletion Cases • If leaf has 2 items, remove one item (done) • If leaf has 1 item – If sibling has 2 items, redistribute items among sibling, parent, and leaf – If sibling has 1 item, slide an item down from the parent to the sibling (merge) – Recursively redistribute and merge up the tree until no change is needed, or root is reached. (If root becomes empty, replace by its child) • Fig. 11. 42 -11. 47, p. 602 -603

Going Another Step • If 2 -3 trees are good, why not make bigger nodes? • 2 -3 -4 trees have 3 kinds of nodes • Remember a node is described by the number of children. It contains one less value than children • So, a 4 -node has 4 children and 3 values. • Names of children are left, middle-left, middleright, and right

4 -node is equivalent to 3 2 -nodes • 4 node has 3 values e. g. <10, 20, 30> • A binary tree of those values would have the middle value (20) as the parent, and the outer values (10, 20) as the children • So every 4 -node can be replaced by 3 2 nodes. • This leads naturally to a very nice insertion algorithm.

Insert into 2 -3 -4 tree • Find the place for the item in the usual way. • On the way down the tree, if you see any 4 -nodes, split them and pass the middle value up. • If the leaf is a 2 -node or 3 -node, add the item to the leaf. • If the leaf is a 4 -node, split it into 2 2 -nodes, passing the middle value up to the parent node, then insert the item into the appropriate leaf node. • There will be room, because 4 -nodes were split on the way down!

2 -3 -4 Insert Example 6, 15, 25 2, 4, 5 10 18, 20 Insert 24, then 19 30

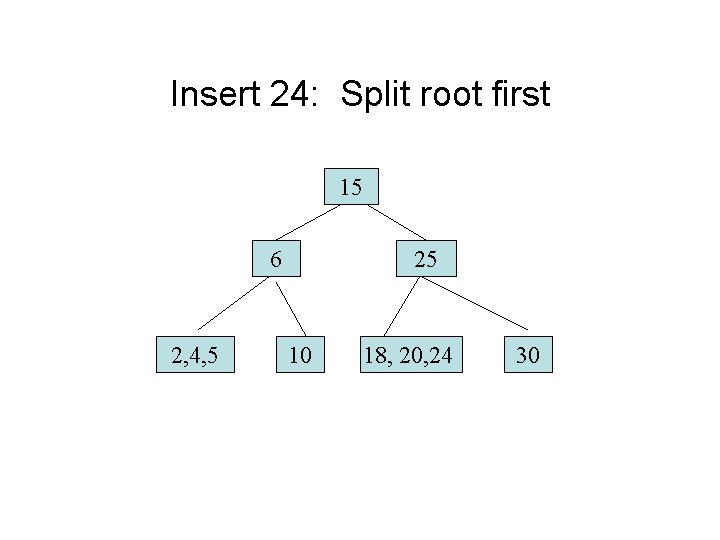
Insert 24: Split root first 15 6 2, 4, 5 25 10 18, 20, 24 30

Insert 19, Split leaf (20 up) first 15 6 2, 4, 5 20, 25 10 18, 19 24 30

2 -3 -4 Algorithm is Simpler • All splits happen on the way down the tree • Therefore, there is always room in the leaf for the insertion • And there is always room in the parent for a node that has to move up (because if the parent were a 4 -node, it would already have been split!)

Deleting from a 2 -3 -4 Tree • Find the value to be deleted and swap with inorder successor. • On the way down the tree (both for value and successor), upgrade 2 -nodes into 3 -nodes or 4 nodes. This ensures that the deleted value will be in a 3 -node or 4 -node leaf • Remove the value from the leaf.

Upgrade cases • 2 -node whose next sibling is a 2 -node – Combine sibling values and “divider” value from parent into a 4 -node – By the algorithm, parent cannot be a 2 -node unless it is the root; in this case, our new 4 -node becomes the root • 2 -node whose next sibling is a 3 -node – Move this value up to parent, move divider value down, shift a value to sibling

Red-Black Trees • Red-Black trees are binary trees • But each node has an additional piece of information (color) • Red nodes can be considered (with their parents) as 3 -nodes or 4 -nodes • There can never be 2 red nodes in a row!

Advantages of Red-black trees • Binary tree search algorithm and traversals hold directly (ignore color) • 2 -3 -4 tree insert and delete algorithms keep tree balanced (consider color)

Splitting a 4 -node • A 4 -node in a RB tree looks like a black node with two red children. • If you make it a red node with 2 black children, you have split the node (and passed the parent up). • If the parent is red, you have to split it too.

Revising a 3 -node • To avoid having two red children in a row, you might have to rotate as well as color change. • When the parent is red: – If the parent’s value is between the child’s and the grandparent’s, do a single rotation – If the child’s value is between the parent’s and the grandparent’s, do a double rotation

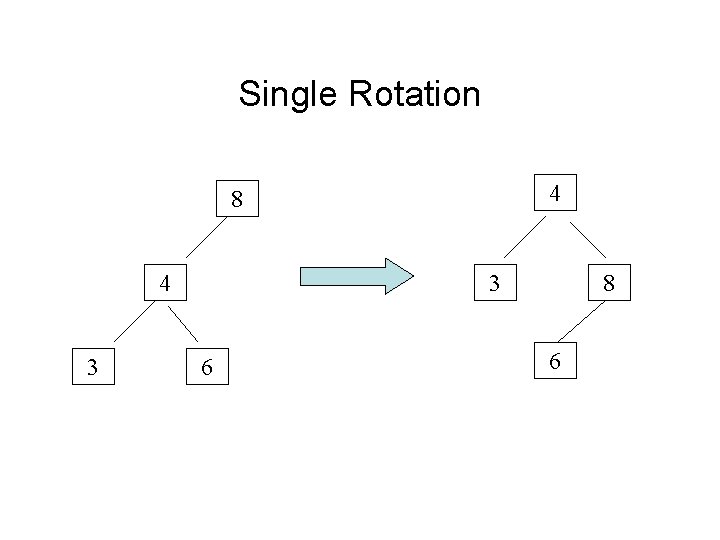
Single Rotation 4 8 4 3 3 6 8 6

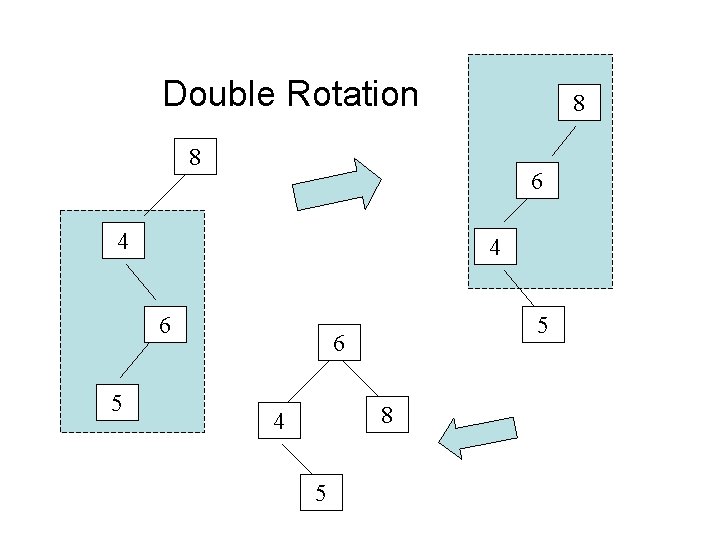
Double Rotation 8 8 6 4 4 6 5 5 6 8 4 5

Top Down Insertion Algorithm • Search the binary tree in the usual way for the insertion algorithm • If you pass a 4 -node (black node with two red children) on the way down, split it • Insert the node as a red child, and use the split algorithm to adjust via rotation if the parent is red also. • Force the root to be black after every insertion.

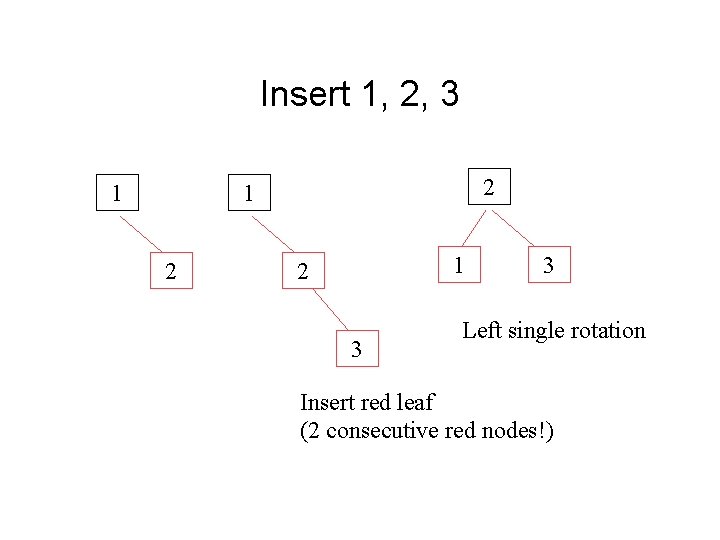
Insert 1, 2, 3 1 2 1 2 3 3 Left single rotation Insert red leaf (2 consecutive red nodes!)

Continued: Insert 4, 5 2 1 2 3 1 4 4 -node (2 red children) split on the way down Root remains black 2 3 1 4 3 4 5 5 Single rotation to avoid consecutive red nodes

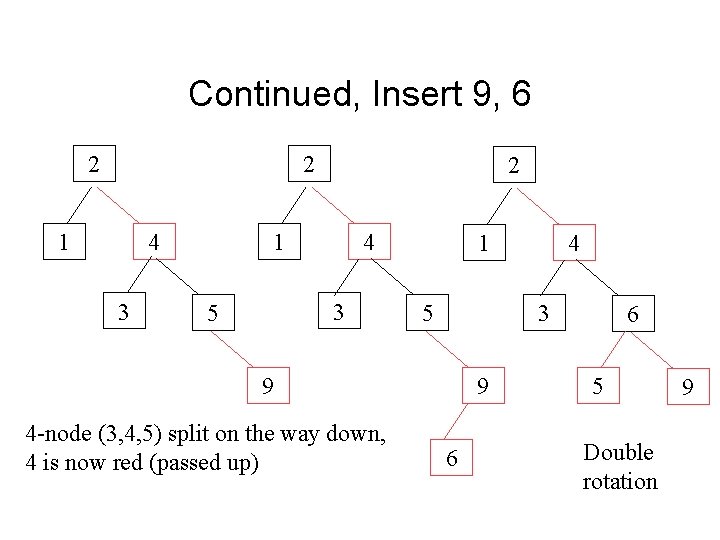
Continued, Insert 9, 6 2 2 1 4 3 5 1 5 3 9 4 -node (3, 4, 5) split on the way down, 4 is now red (passed up) 4 9 6 6 5 Double rotation 9

Deletion Algorithm • Find the node to be deleted (NTBD) – On the way down, if you pass a 2 -node upgrade it by borrowing from its neighbor and/or parent • If the node is not a leaf node, – Find its immediate successor, upgrading all 2 nodes – Swap value of leaf node with value of NTBD • Remove the current leaf node, which is now NTBD (because of swap, if it happened)

Red-black “neighbor” of a node • Let X be a 2 -node to be deleted • If X is its parent’s left child, X’s right neighbor can be found by: – Let S = parent’s right child. If S is black, it is the neighbor – Otherwise, S’s left child is the neighbor. • If X is parent’s left child, then X’s left neighbor is grandparent’s left child.

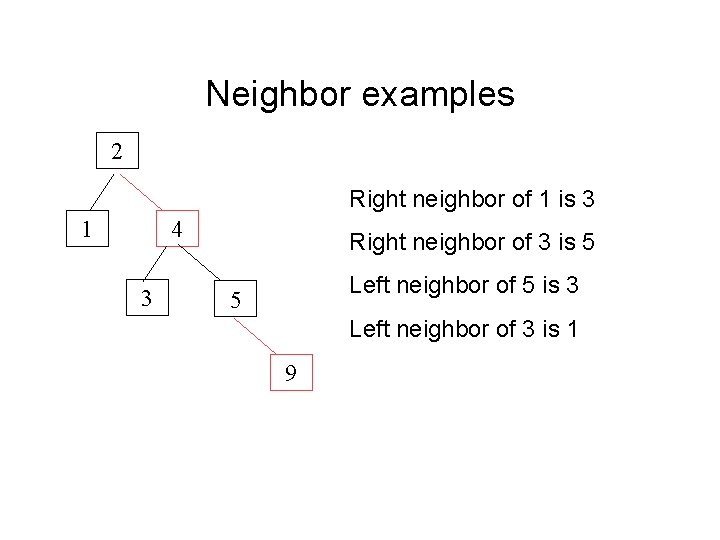
Neighbor examples 2 Right neighbor of 1 is 3 1 4 3 Right neighbor of 3 is 5 Left neighbor of 5 is 3 5 Left neighbor of 3 is 1 9

Upgrade a 2 -node • Find the 2 -node’s neighbor (right if any, otherwise left) • If neighbor is also a 2 -node (2 black children) – Create a 4 -node from neighbors and their parent. – If neighbors are actually siblings, this is a color swap. – Otherwise, it requires a rotation • If neighbor is a 3 -node or 4 -node (red child) – Move “inner value” from neighbor to parent, and “dividing value” from parent to 2 -node. – This is a rotation

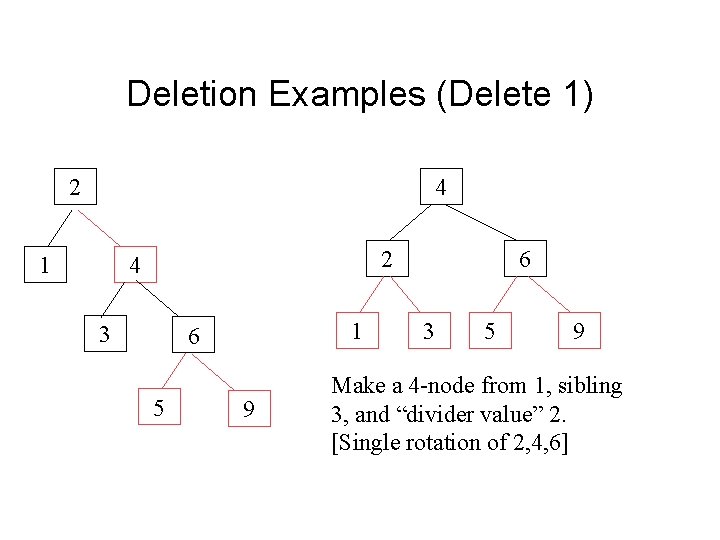
Deletion Examples (Delete 1) 2 4 1 2 4 3 1 6 5 9 6 3 5 9 Make a 4 -node from 1, sibling 3, and “divider value” 2. [Single rotation of 2, 4, 6]

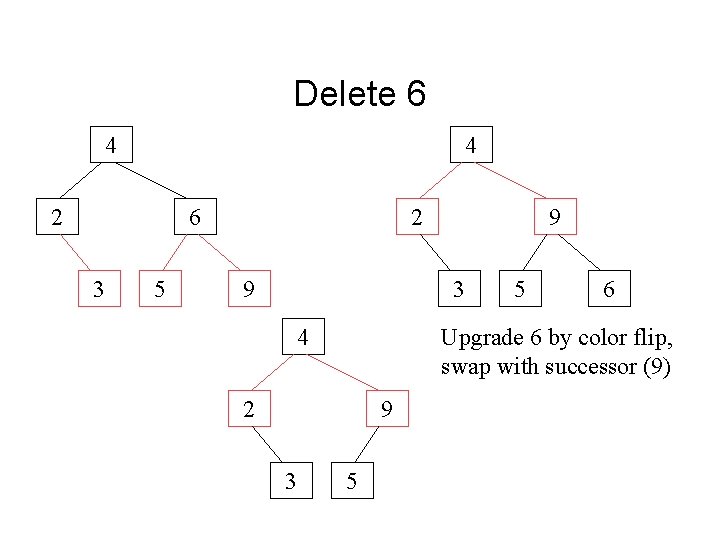
Delete 6 4 4 2 6 3 5 2 9 9 3 4 6 Upgrade 6 by color flip, swap with successor (9) 2 9 3 5 5

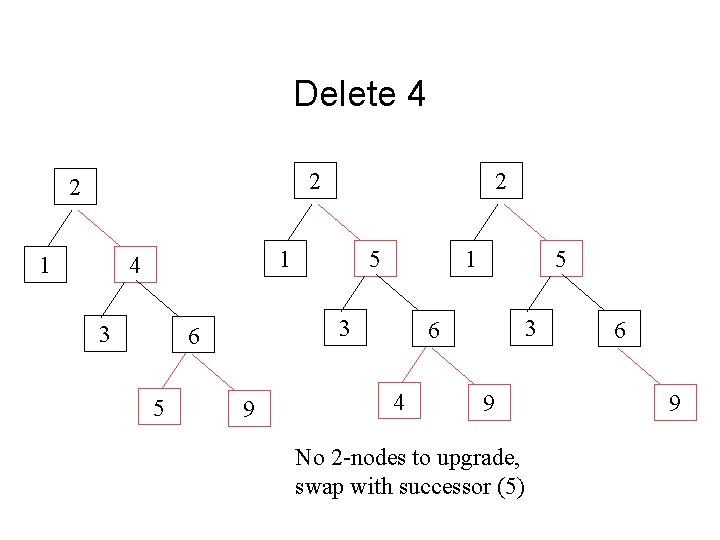
Delete 4 2 2 1 4 3 1 3 6 5 5 9 5 3 6 4 9 No 2 -nodes to upgrade, swap with successor (5) 6 9

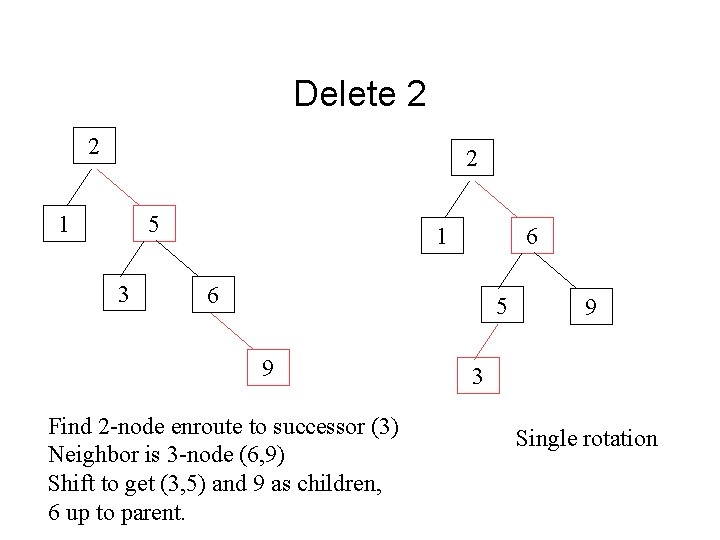
Delete 2 2 2 1 5 3 1 6 6 5 9 Find 2 -node enroute to successor (3) Neighbor is 3 -node (6, 9) Shift to get (3, 5) and 9 as children, 6 up to parent. 9 3 Single rotation

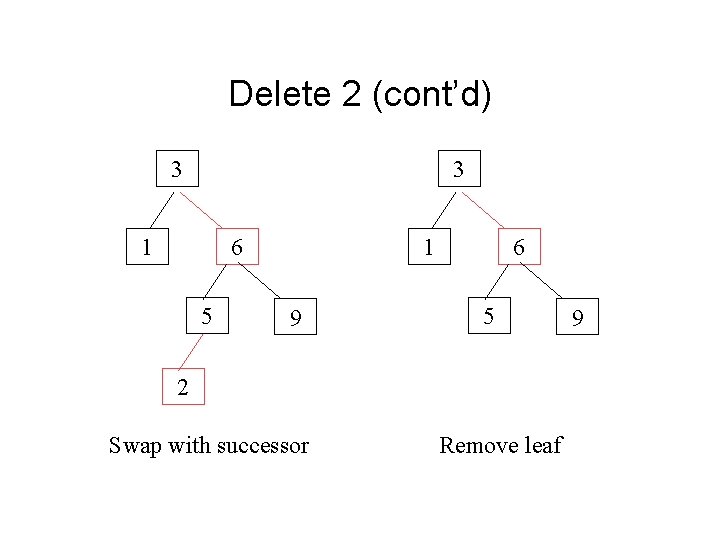
Delete 2 (cont’d) 3 3 1 6 5 1 9 6 5 2 Swap with successor Remove leaf 9