Balanced Search Trees l BST efficient lookup insertion

Balanced Search Trees l BST: efficient lookup, insertion , deletion Ø Average case: O(log n) for all operations since find is O(log n) [complexity of insert after find is O(1), why? ] Ø l Worst case is bad, what's big-Oh? What's the tree shape? Balanced Search trees Ø Use rotations to maintain balance, different implementations rotate/rebalance at different times Ø AVL tree is conceptually simple, bookkeeping means coefficient for big-Oh is higher than other ideas Ø Red-black tree harder to code but good performance: basis for Java map classes and most C++ map classes CPS 100 9. 1

Balance trees we won't study l B-trees are used when data is both in memory and on disk Ø File systems, really large data sets Ø Rebalancing guarantees good performance both asymptotically and in practice. Differences between cache, memory, disk are important l Splay trees rebalance during insertion and during search, nodes accessed often more closer to root Ø Other nodes can move further from root, consequences? • Performance for some nodes gets better, for others … Ø CPS 100 No guarantee running time for a single operation, but guaranteed good performance for a sequence of operations, this is good amortized cost (vector push_back) 9. 2

Balanced trees we will study l l l Both kinds have worst-case O(log n) time for tree operations AVL (Adel’son-Velskii and Landis), 1962 Ø Nodes are “height-balanced”, subtree heights differ by 1 Ø Rebalancing requires per-node bookkeeping of height Ø http: //www. seanet. com/users/arsen/avltree. html Red-black tree uses same rotations, but can rebalance in one pass, contrast to AVL tree Ø In AVL case, insert, calculate balance factors, rebalance Ø In Red-black tree can rebalance on the way down, code is more complex, but doable Ø STL in C++ uses red-black tree for map and set classes Ø Standard java. util. Tree. Map/Tree. Set use red-black CPS 100 9. 3

Balanced Trees in Practice l See usetreeset. cpp Ø Balanced and unbalanced search trees as basis for sets Ø Contrast with red-black trees in STL, see setstl. cpp l Reasons STL code is faster than AVL code? Ø Intrinsically better algorithm, one pass v. two pass Ø Makes better use of storage allocation? (conceivably) Ø More/better programming? l Reading code: STL v. Java implementations Ø What does tradition tell us? CPS 100 9. 4

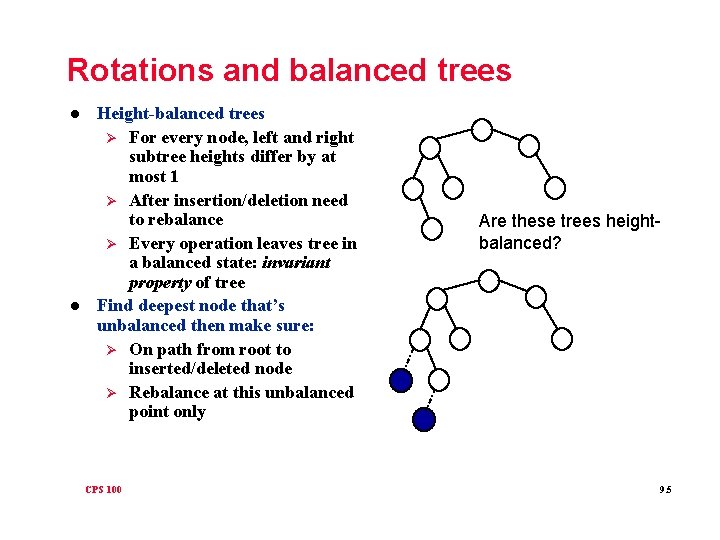
Rotations and balanced trees l l Height-balanced trees Ø For every node, left and right subtree heights differ by at most 1 Ø After insertion/deletion need to rebalance Ø Every operation leaves tree in a balanced state: invariant property of tree Find deepest node that’s unbalanced then make sure: Ø On path from root to inserted/deleted node Ø Rebalance at this unbalanced point only CPS 100 Are these trees heightbalanced? 9. 5

Rotation to rebalance N N C A B l A B C When a node N (root) is unbalanced height differs by 2 (must be more than one) Ø Change N->left • do. Left Ø Change N->left->right • do. Left. Right Tree * do. Left(Tree * root) Ø Change N->right->left • do. Right. Left { Ø Change N->right Tree * new. Root = root->left; root->left = new. Root->right; • do. Right new. Root->right = root; l First/last cases are symmetric return new. Root; l Middle cases require two rotations } Ø First of the two puts tree into do. Left or do. Right CPS 100 9. 6

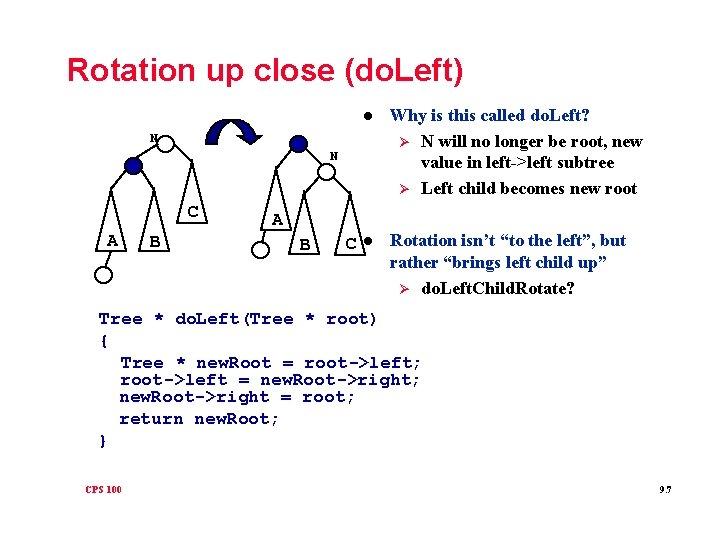
Rotation up close (do. Left) l Why is this called do. Left? Ø N will no longer be root, new value in left->left subtree Ø Left child becomes new root l Rotation isn’t “to the left”, but rather “brings left child up” Ø do. Left. Child. Rotate? N N C A B C Tree * do. Left(Tree * root) { Tree * new. Root = root->left; root->left = new. Root->right; new. Root->right = root; return new. Root; } CPS 100 9. 7

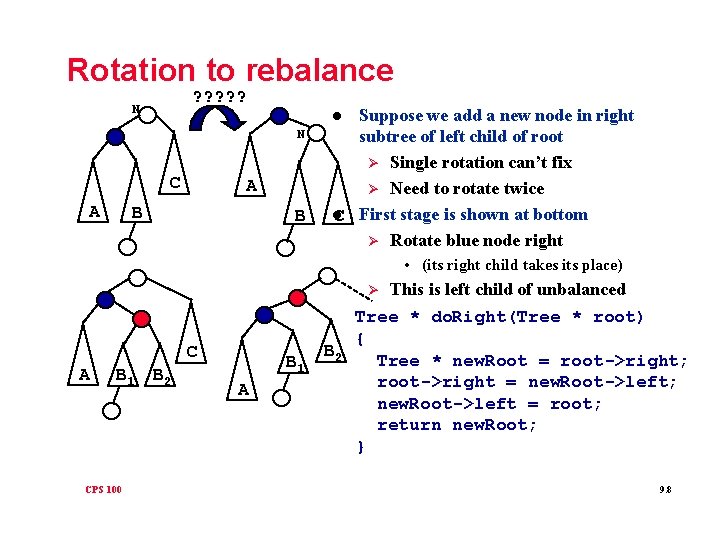
Rotation to rebalance ? ? ? N N C A Suppose we add a new node in right subtree of left child of root Ø Single rotation can’t fix Ø Need to rotate twice l C First stage is shown at bottom Ø Rotate blue node right l A B B • (its right child takes its place) Ø C A B 1 CPS 100 B 2 B 1 A B 2 This is left child of unbalanced Tree * do. Right(Tree * root) { Tree * new. Root = root->right; root->right = new. Root->left; new. Root->left = root; return new. Root; } 9. 8

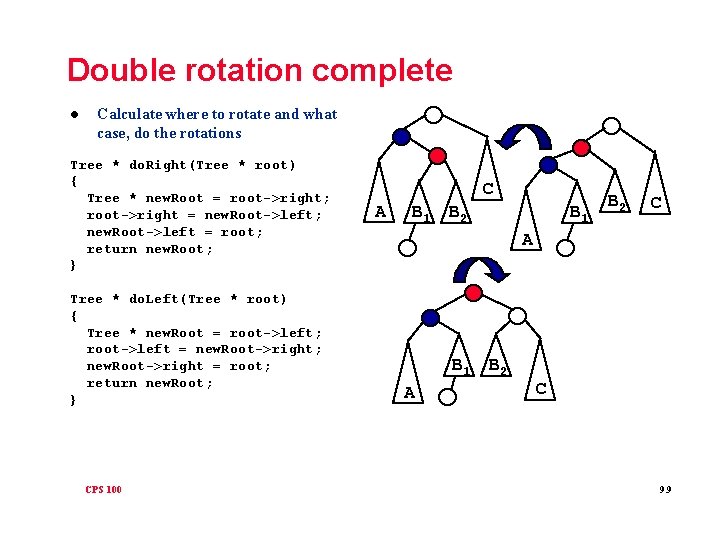
Double rotation complete l Calculate where to rotate and what case, do the rotations Tree * do. Right(Tree * root) { Tree * new. Root = root->right; root->right = new. Root->left; new. Root->left = root; return new. Root; } Tree * do. Left(Tree * root) { Tree * new. Root = root->left; root->left = new. Root->right; new. Root->right = root; return new. Root; } CPS 100 C A B 1 B 2 C A B 1 A B 2 C 9. 9

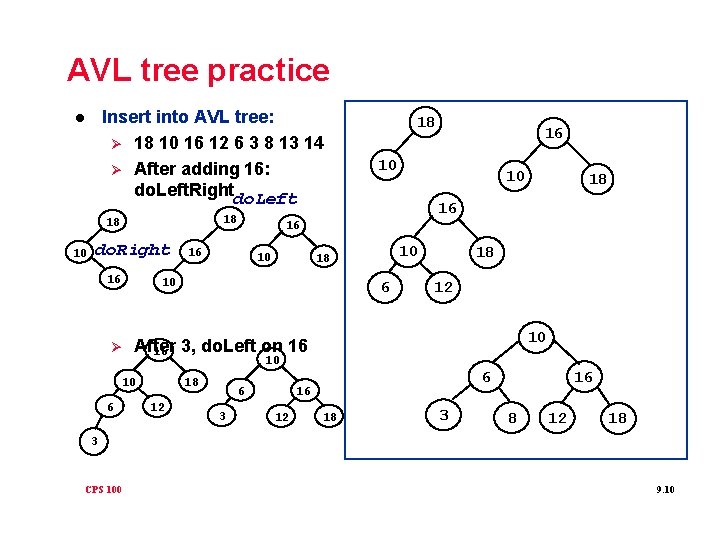
AVL tree practice Insert into AVL tree: Ø 18 10 16 12 6 3 8 13 14 Ø After adding 16: do. Left. Rightdo. Left l 18 18 10 do. Right 16 10 10 18 16 16 10 10 18 6 18 12 10 After 16 3, do. Left on 16 10 10 6 16 16 10 Ø 18 18 12 6 3 6 16 12 18 3 16 8 12 18 3 CPS 100 9. 10

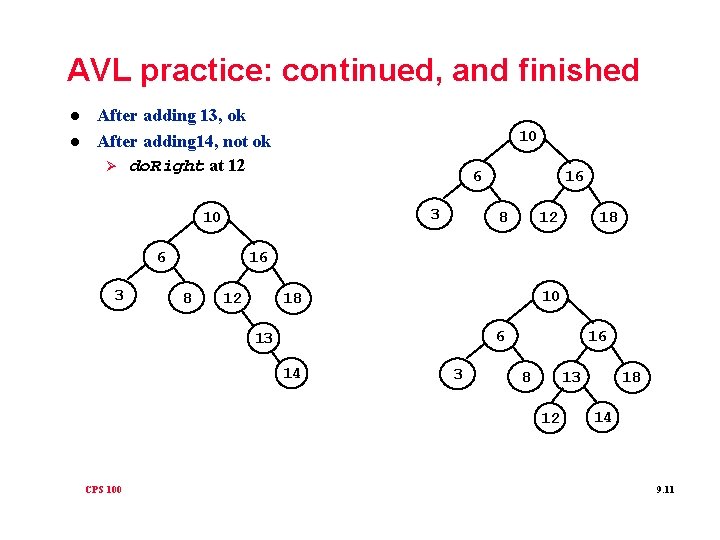
AVL practice: continued, and finished l l After adding 13, ok After adding 14, not ok Ø do. Right at 12 10 6 3 16 8 12 10 18 6 13 14 3 16 8 13 12 CPS 100 18 18 14 9. 11

Rodney Brooks l l Flesh and Machines: “We are machines, as are our spouses, our children, and our dogs. . . I believe myself and my children all to be mere machines. But this is not how I treat them in a very special way, and I interact with them on an entirely different level. They have my unconditional love, the furthest one might be able to get from rational analysis. ” Director of MIT AI Lab CPS 100 9. 12