Balance in Binary Trees Impact on Performance Creative

Balance in Binary Trees Impact on Performance Creative Commons License – Curt Hill.

Tree Shape and Performance • A tree that is balanced has excellent performance • O(log 2 N) for: – Searches – Insertions – Deletions • Only a hash table can beat this performance – But it has its own issues Creative Commons License – Curt Hill.

What is balance? • The notion is that the two sub-trees are of about the same size • Thus a search eliminates half the tree in each examination • Perfect balance: – For each node in the tree, the size of the two sub-trees are off by at most one Creative Commons License – Curt Hill.

Probabilities • What is the likelihood that a randomly built tree will have good performance characteristics? • This is a difficult question • The shape of a tree is dependent on the entry order of the nodes to be inserted • Example: – Consider the integers 1 -7 as the items to put in a tree – There are 7! = 5040 ways to order their input • 7 ways to choose first • 6 ways to choose second • etc. Creative Commons License – Curt Hill.

What do we want? 4 2 1 6 3 5 A search must look at no more than 3 nodes Creative Commons License – Curt Hill. 7

Example Continued • There are two really bad ways to choose the tree: – In ascending order or descending order – There are only two of these but there are several others that are just as bad – Consider 1 7 6 5 4 3 2 or • 1237654 • Bad in this case means that every node has zero or one descendents Creative Commons License – Curt Hill.

What do we not want? 1 1 2 Arrival in ascending order 3 Equally bad 2 3 4 7 5 5 6 6 4 7 A search must look at no more than 7 nodes Creative Commons License – Curt Hill.

Negative Combinatorics • There are two ways to choose the first item – Each subsequent item provides two ways: – The next item in ascending order – The last item – Therefore 2 * 2 * 2 * 1 – Looks like 64 ways to choose a list – This is 1. 27% chance of a list • A search would look at no more than 7 nodes Creative Commons License – Curt Hill.

Positive Combinatorics • There is only one way to choose the root, it must be the 4 • There are two ways to choose the second: 2 or 6 • There are three ways to choose third – If 2 was picked the 6 or any descendent of 2 – If 6 was picked the 2 or any descendent of 6 • It gets exciting after that Creative Commons License – Curt Hill.

Positive Combinatorics • Sub-cases need to be examined of the three last choices • These do not work well in this kind of presentation • I believe that there are 80 out of 5040 (1. 5%) permutations that yield a perfectly balance tree • However, most possibilities fall somewhere in between maximum pathes of 7 and 3 Creative Commons License – Curt Hill.

Summary • The worst case is a linked list which is bad – The worst case is not very likely • The best case is perfectly balanced – The best case is more likely, but still unlikely • Empirical studies indicate that the average path length of a unbalanced tree to be only 39% longer than a perfectly balanced tree • Balancing is hard and slows insertions and deletions Creative Commons License – Curt Hill.

When to Balance • In most cases an unbalanced tree will perform quite adequately • If the application fulfills the following two criteria then balancing could be considered – The data is large and the search performance impacts the program – The number of searches is large compared to insertion and deletion Creative Commons License – Curt Hill.

Perfectly balanced trees • Definition: – For each node the number of nodes of the left and right sub-trees differ by only 1 • Balancing a tree is a recursive process that involves nodes from the leaves to root • It is usually the case that control information is placed in node that measures the balance Creative Commons License – Curt Hill.

Balance Again • Balancing occurs in insertion and deletion, but not searches • It is somewhat intricate so perfect balance is seldom used • The ratio of searches to inserts and deletes must be very high • Is there another definition of balance that gives good performance with less rebalancing Creative Commons License – Curt Hill.

Height Balanced • Also known as AVL balance – Adelson, Velski and Landis – Developed it and proved its desirability • Definition: – The tree is balanced if for each node the heights of the two sub-trees differ at most by one • It is the height of the tree that determines the worst case search Creative Commons License – Curt Hill.

Digression on Search • Consider searching an array • On average the search requires ½N comparisons • The worst case is N searchs to find last one or to show not found • The average and worst case are quite different • This is not the case for trees Creative Commons License – Curt Hill.

Searching Trees 4 2 1 6 3 5 7 More than half the nodes are leaves at maximum depth. Worst case is three probes, but average case is only slightly less than three probes. Creative Commons License – Curt Hill.

AVL Trees Again • Adelson, Velski and Landis proved: – Worst case of an AVL tree is only 45% worse than perfectly balanced – Average case: Insignificantly different than perfectly balanced • Every perfectly balanced is also AVL balanced • Far fewer rebalances, thus cheaper to construct – For the most part rebalancing occurs when really needed Creative Commons License – Curt Hill.

Construction • Consider the construction of the following tree • Four types of rebalancing operation – RR single – LL single – LR double – RL double • Add: 4 5 7 2 1 3 6 Creative Commons License – Curt Hill.

After 2 inserts 4 5 Still perfectly balanced Creative Commons License – Curt Hill.

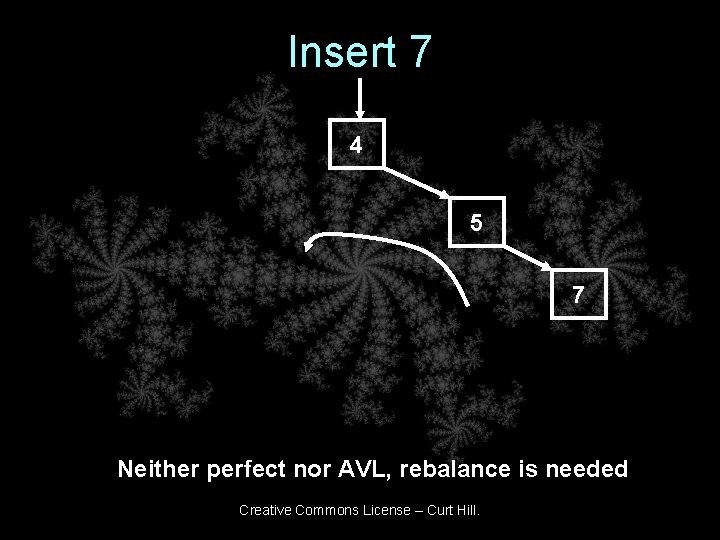
Insert 7 4 5 7 Neither perfect nor AVL, rebalance is needed Creative Commons License – Curt Hill.

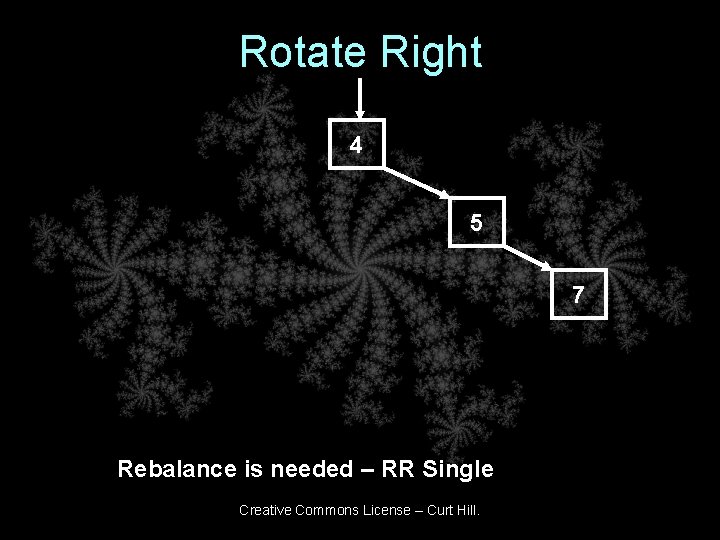
Rotate Right 4 5 7 Rebalance is needed – RR Single Creative Commons License – Curt Hill.

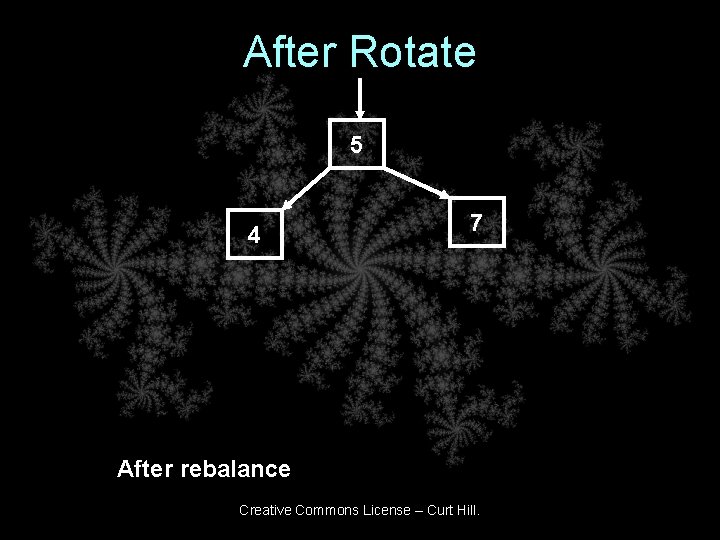
After Rotate 5 4 7 After rebalance Creative Commons License – Curt Hill.

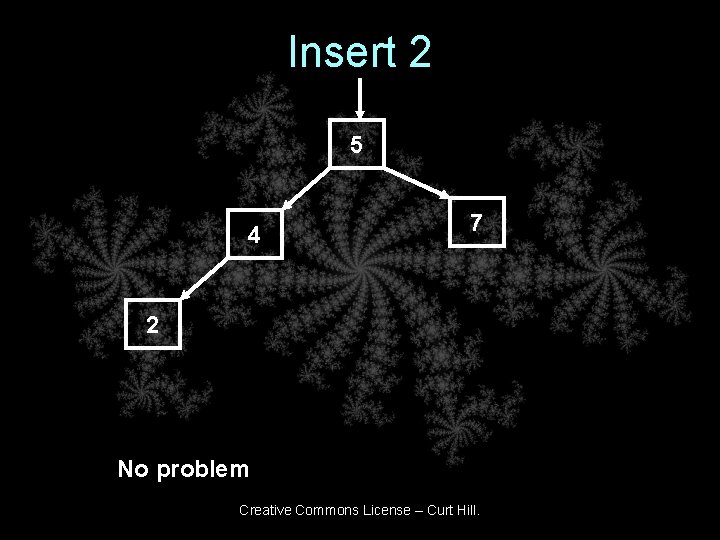
Insert 2 5 4 7 2 No problem Creative Commons License – Curt Hill.

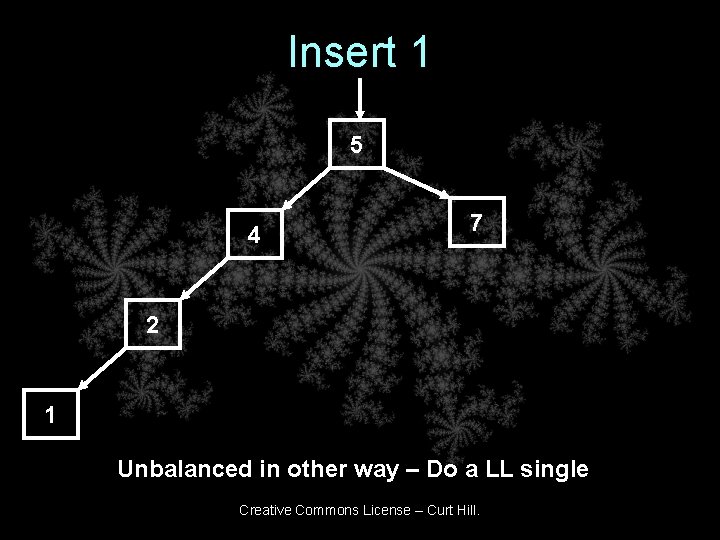
Insert 1 5 4 7 2 1 Unbalanced in other way – Do a LL single Creative Commons License – Curt Hill.

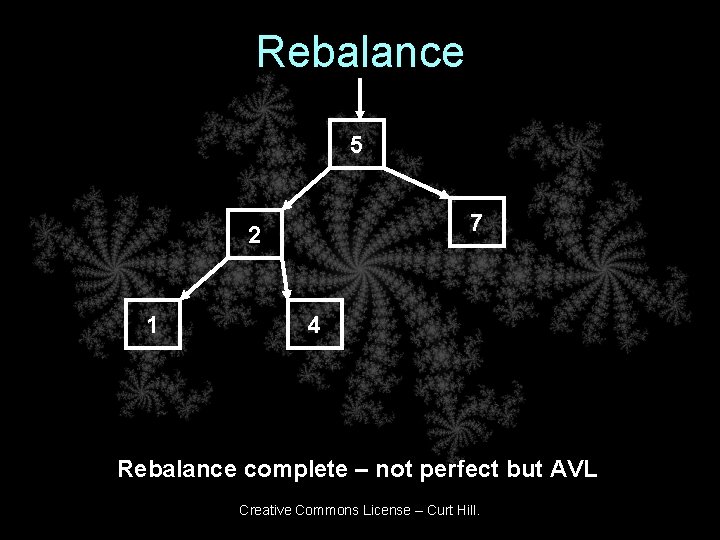
Rebalance 5 7 2 1 4 Rebalance complete – not perfect but AVL Creative Commons License – Curt Hill.

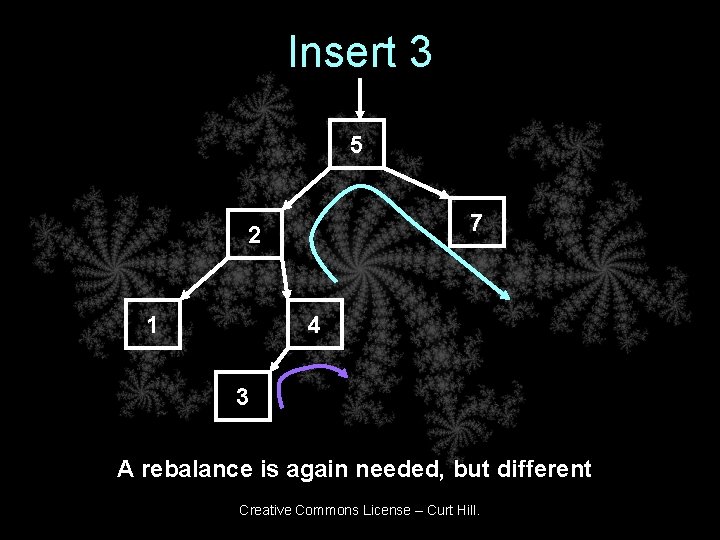
Insert 3 5 7 2 1 4 3 A rebalance is again needed, but different Creative Commons License – Curt Hill.

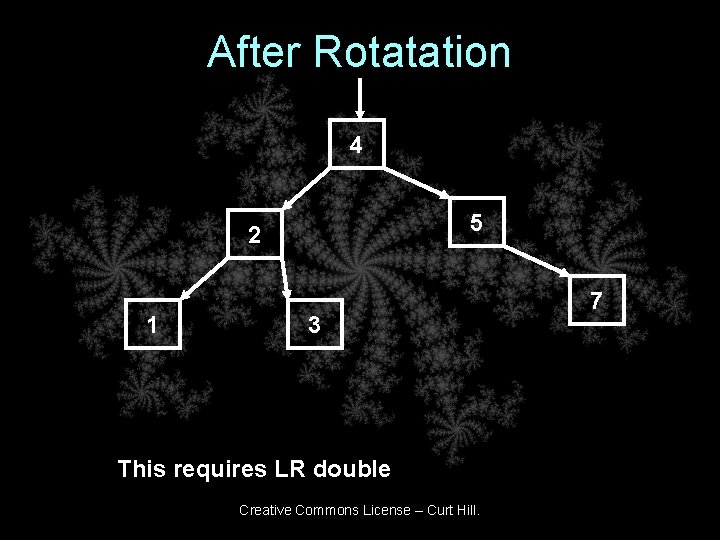
After Rotatation 4 5 2 1 3 This requires LR double Creative Commons License – Curt Hill. 7

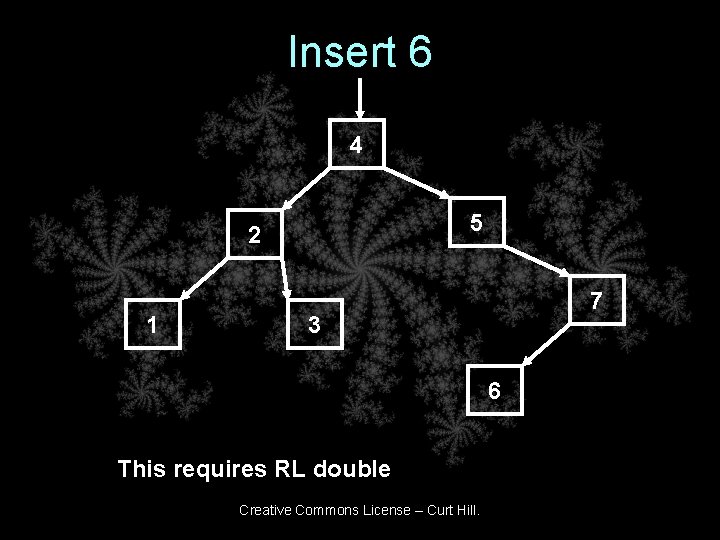
Insert 6 4 5 2 1 7 3 6 This requires RL double Creative Commons License – Curt Hill.

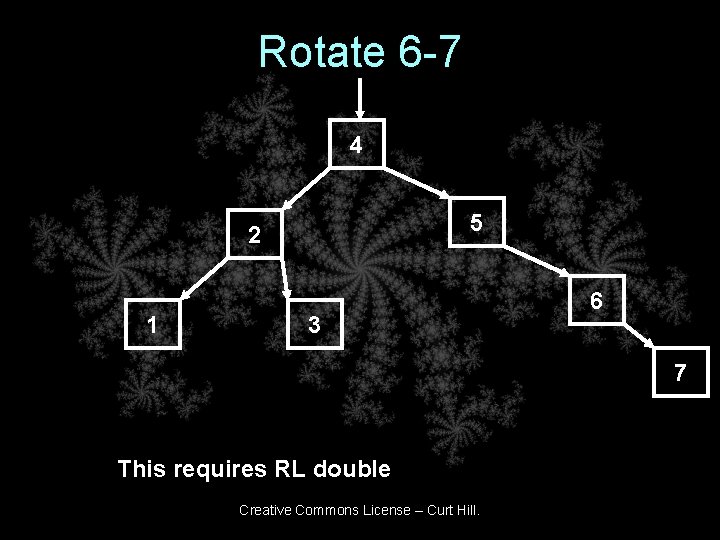
Rotate 6 -7 4 5 2 1 3 6 7 This requires RL double Creative Commons License – Curt Hill.

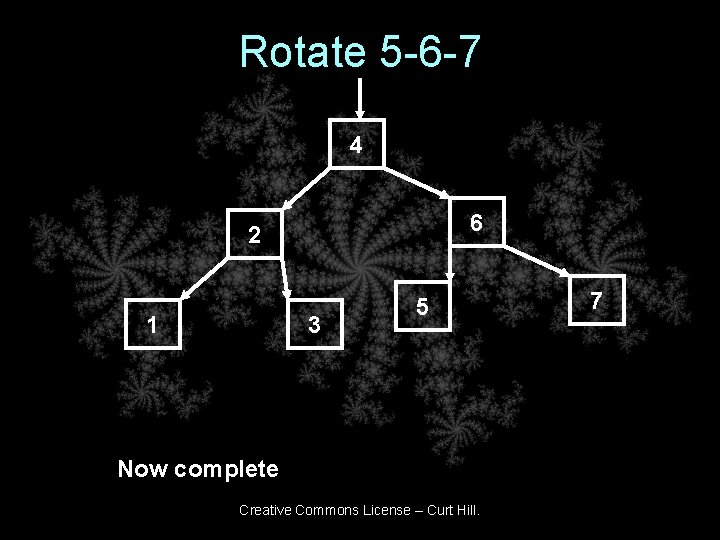
Rotate 5 -6 -7 4 6 2 1 3 5 Now complete Creative Commons License – Curt Hill. 7

The problem of balancing • To implement requires extra stuff in the nodes • Measures the height of the descendents • Even with an AVL tree there is substantial work to be done at insertion and deletion time • Thus the search to insert and delete ratio needs to be high – Just not as high as perfect balance Creative Commons License – Curt Hill.

Synonyms • Another name for an AVL trees is Fibonacci tree • The fact that heights may disagree by one leads to as strangely asymmetric tree Creative Commons License – Curt Hill.

Is this balanced? 5 2 1 8 3 6 4 10 7 9 11 12 Creative Commons License – Curt Hill.