BAHASA REGULAR PENDAHULUAN n n Bahasa regular adalah

BAHASA REGULAR

PENDAHULUAN n n Bahasa regular adalah penyusun ekspresi reguler (ER) Ekspresi reguler terdiri dari kombinasi simbol-simbol atomik menggunakan 3 operasi yaitu : – katenasi, – alternasi, dan – repetisi /closure n n Pada kasus scanner, simbol-simbol atomik adalah karakter-karakter di dalam program sumber. Dua buah ekspresi regular adalah ekuivalen jika keduanya menyatakan bahasa yang sama

Operasi Regular - katenasi n Katenasi /konkatenasi atau sequencing disajikan dengan physical adjacency – e. g. ekspresi regular ‘<letter> <digit>’ bentuk penyajian sederhana (diasumsikan sebagai definisi yang jelas dari letter dan digit) komposisi terurut dari letter diikuti dengan digit » “<” dan “>” digunakan untuk mengidentifikasi simbol-simbol yang merepresentasikan simbol spesifik (menggunakan ekspresi regular) » Kita bisa menggunakan “: : =” (ekivalensi) untuk menggabungkan ekspresi regular yang didefinisikan dengan <letter> dan <digit>

Operasi Regular - alternasi n Alternasi membolehkan pilihan dari beberapa pilihan dan biasanya disajikan dengan operator ‘|’ – E. g. <digit> : : = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 » contoh yang menggunakan juga operator ekivalensi n Bentuk tulisan cepat tertentu juga biasanya digunakan dengan alternasi (khususnya ellips) – E. g. <letter> : : = a | b | … | z | A | B | … | Z » Can use the ellipses (“…”) when a sequence is well defined

Operasi Regular - repetisi n n Terakhir, repetisi membolehkan ekspresi dari kontruksi yang diulang beberapa kali Terdapat 2 operator yang digunakan yaitu superscript ‘+’ dan superscript ‘*’ – E. g. <word> : : = <letter>+ » this implies a word consists of one or more letters (* would imply zero or more letters and a word must have at least one letter so we use +)
![Ekivalensi ER [1] Contoh : L = {aba n 1, m 1} er = Ekivalensi ER [1] Contoh : L = {aba n 1, m 1} er =](http://slidetodoc.com/presentation_image_h2/c86904b0657c1a5d4b573764af9f8203/image-6.jpg)
Ekivalensi ER [1] Contoh : L = {aba n 1, m 1} er = a b a L= {aba n 0, m 0} er = a* b a* n Perhatikan bahwa kita tidak bisa membuat ekspresi regular dari bahasa L = {aba n 1} atau L = {aba n 0}, karena keduanya tidak dihasilkan dari grammar regular.
![Ekivalensi ER[2] n (a b)* a = a (b a)* Bukti : (a b)* Ekivalensi ER[2] n (a b)* a = a (b a)* Bukti : (a b)*](http://slidetodoc.com/presentation_image_h2/c86904b0657c1a5d4b573764af9f8203/image-7.jpg)
Ekivalensi ER[2] n (a b)* a = a (b a)* Bukti : (a b)* a = ( (ab) (abab) …) a = ( a (aba) (ababa) …) = (a (aba) (ababa) …) = a ( (ba) (baba) …) = a (b a)*

Ekivalensi AHN, AHD, dan GR n AHD bisa dibentuk dari AHN. GR bisa dibentuk dari AHD. n AHN bisa dibentuk dari GR. n

Pembentukan AHD dari AHN Diberikan sebuah AHN F = (K, V, M, S, Z). Akan dibentuk sebuah AHD F’ = (K’, V’, M’, S’, Z’) dari AHN F tersebut. Algoritma pembentukannya adalah sbb. : n Tetapkan : S’ = S dan V’ = V n Copykan tabel AHN F sebagai tabel AHD F’. Mula-mula K’ = K dan M’ = M n Setiap stata q yang merupakan nilai (atau peta) dari fungsi M dan q K, ditetapkan sebagai elemen baru dari K’. Tempatkan q tersebut pada kolom Stata M’, lakukan pemetaan berdasarkan fungsi M n Ulangi langkah diatas sampai tidak diperoleh stata baru n Elemen Z’ adalah semua stata yang mengandung stata elemen Z.

Pembentukan GR dari AHD Diketahui sebuah AHD F = (K, V, M, S, Z). Akan dibentuk GR G = (V’, V, S’, Q). Algoritma pembentukan GR dari AHD adalah sebagai berikut : n Tetapkan V’ = V, S’ = S, V = S n Jika A, A K dan a V, maka : M(A, a) = A ekuivalen dengan produksi :

Pembentukan AHN dari GR Diketahui GR G = (V, V, S, Q). Akan dibentuk AHN F = (K, V’, M, S’, Z). Algoritma pembentukan AHN dari GR : n Tetapkan V’ = V, S’ = S, K = V n Produksi A a A ekuivalen dengan M(A, a) = A Produksi A a ekuivalen dengan M(A, a) = X, dimana X V n K = = K {X} n Z = {X}
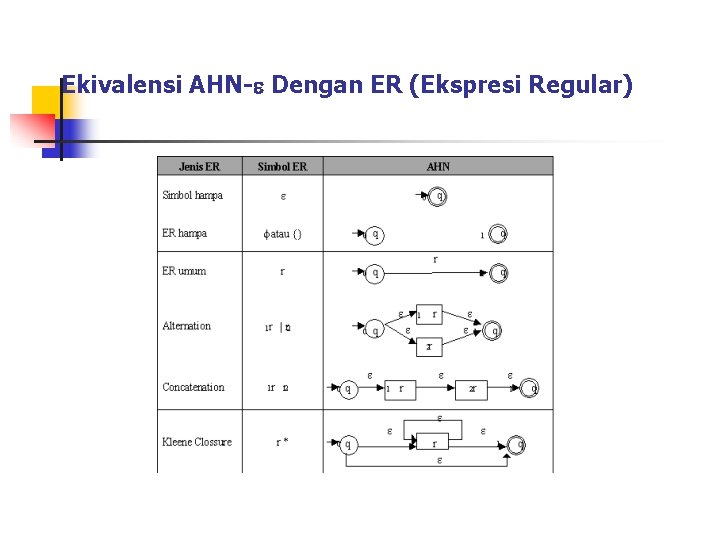
Ekivalensi AHN- Dengan ER (Ekspresi Regular)
- Slides: 12