Backpropagation Last time Correlational learning Hebb rule What

Backpropagation

Last time…

Correlational learning: Hebb rule What Hebb actually said: When an axon of cell A is near enough to excite a cell B and repeatedly and consistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficacy, as one of the cells firing B, is increased. The minimal version of the Hebb rule: When there is a synapse between cell A and cell B, increment the strength of the synapse whenever A and B fire together (or in close succession). The minimal Hebb rule as implemented in a network:

Limitations of Hebbian learning • Many association problems it cannot solve • Especially where similar input patterns must produce quite different outputs. • Without further constraints, weights grow without bound • Each weight is learned independently of all others • Weight changes are exactly the same from pass to pass.

Predictive error-driven learning with linear units…

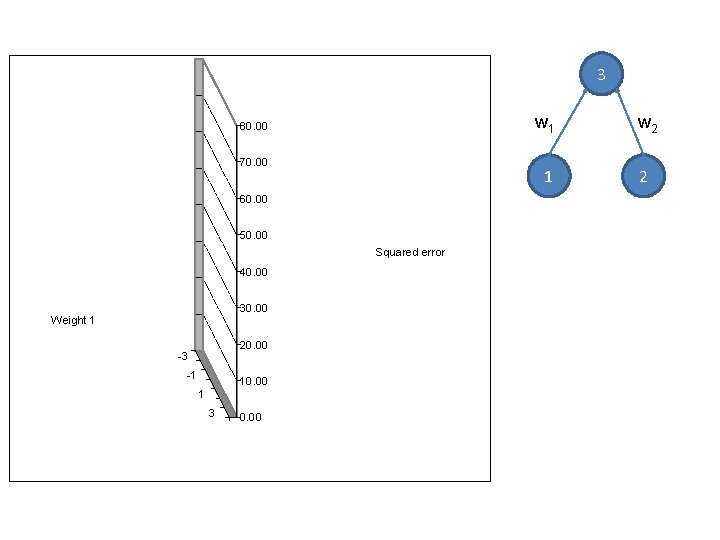
3 80. 00 70. 00 60. 00 50. 00 Squared error 40. 00 30. 00 Weight 1 20. 00 -3 -1 10. 00 1 3 0. 00 w 1 w 2 1 2

Why don’t we just use two-layer perceptrons?

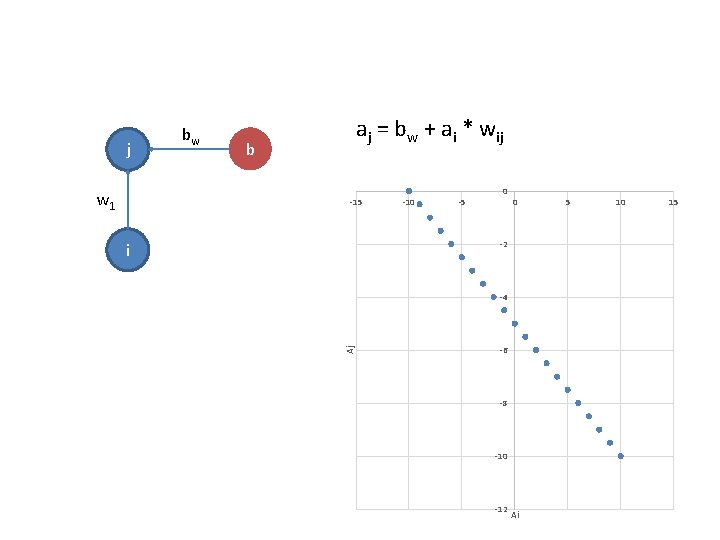
j w 1 bw aj = bw + ai * wij b -15 -10 -5 0 0 -2 i Aj -4 -6 -8 -10 -12 Ai 5 10 15

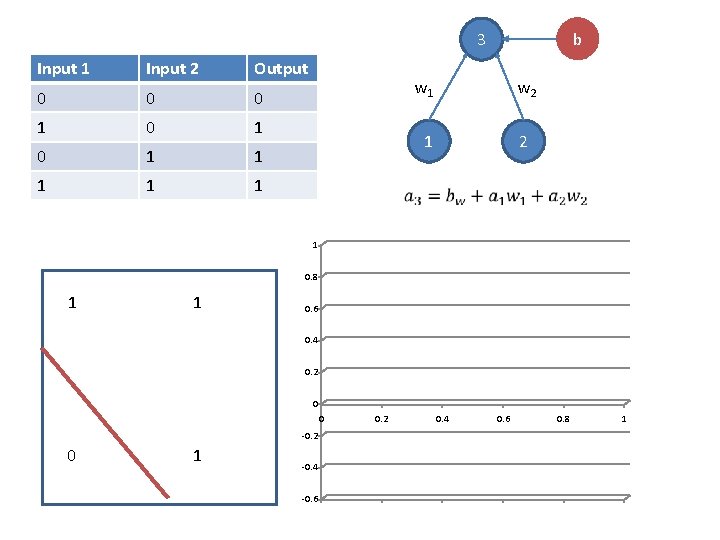
b 3 Input 1 Input 2 Output 0 0 0 1 0 1 1 1 w 2 1 2 1 0. 8 1 1 0. 6 0. 4 0. 2 0 0 -0. 2 0 1 -0. 4 -0. 6 0. 2 0. 4 0. 6 0. 8 1

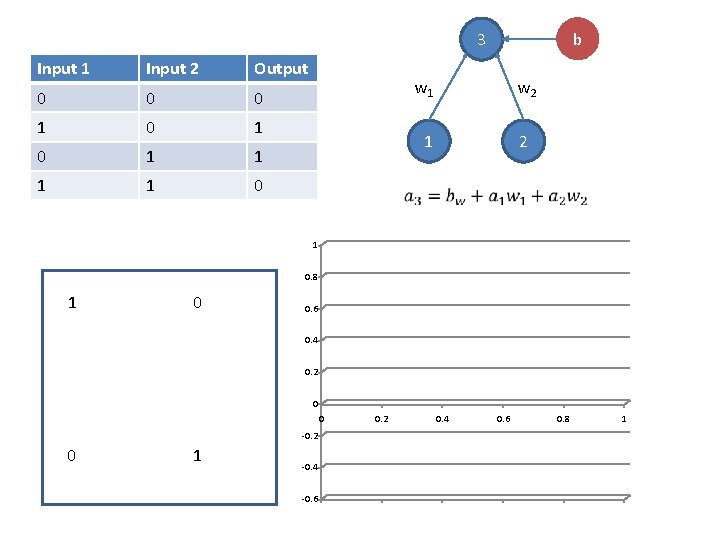
b 3 Input 1 Input 2 Output 0 0 0 1 0 1 1 0 w 1 w 2 1 2 1 0. 8 1 0 0. 6 0. 4 0. 2 0 0 -0. 2 0 1 -0. 4 -0. 6 0. 2 0. 4 0. 6 0. 8 1

Linear separability problem: with linear units (and thresholded linear units), *no solutions exist* for input/output mappings that are not linearly separable. What if we add an extra layer between input and output?

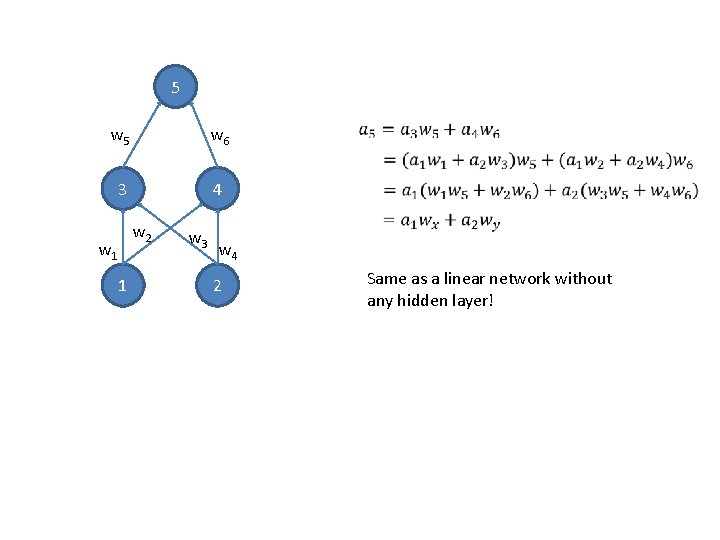
5 w 6 3 4 w 2 w 1 1 w 3 w 4 2 Same as a linear network without any hidden layer!

What if we use thresholded units?

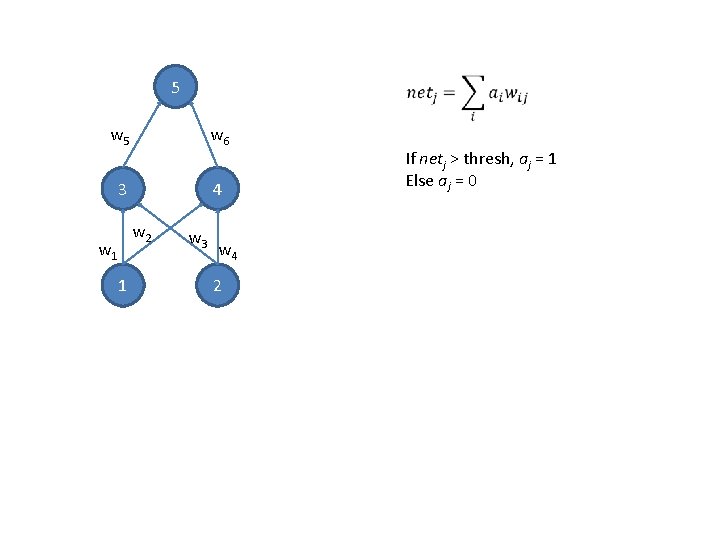
5 w 6 3 4 w 2 w 1 1 w 3 w 4 2 If netj > thresh, aj = 1 Else aj = 0

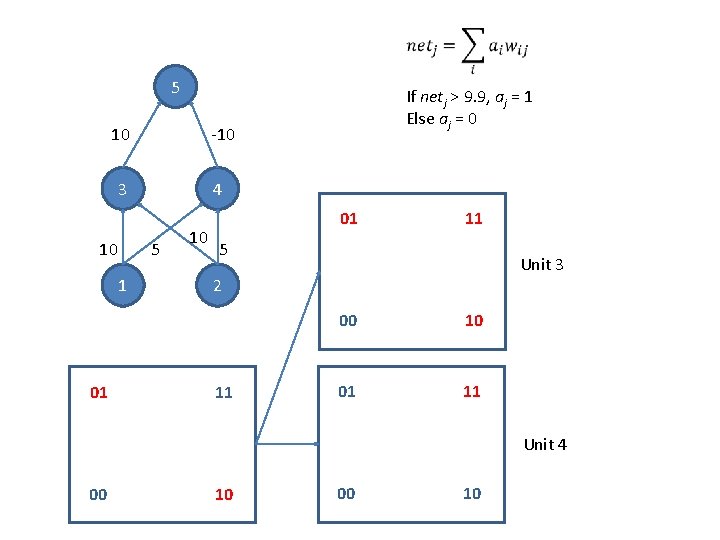
5 10 -10 3 10 01 4 5 1 If netj > 9. 9, aj = 1 Else aj = 0 10 01 11 5 Unit 3 2 11 00 10 01 11 Unit 4 00 10

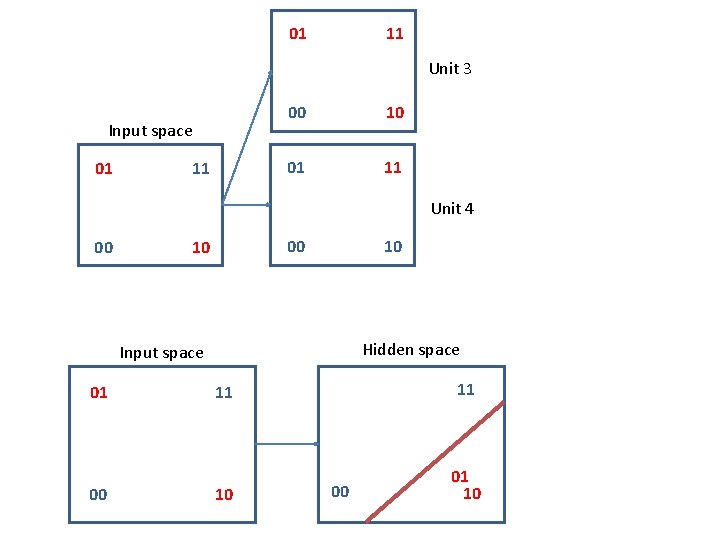
01 11 Unit 3 Input space 01 11 00 10 01 11 Unit 4 00 00 10 10 Hidden space Input space 01 00 11 11 10 00

• So with thresholded units and a hidden layer, solutions exist… • …and solutions can be viewed as “rerepresenting” the inputs, so as to make the mapping to the output unit learnable. • BUT, how can we learn the correct weights instead of just setting them by hand?

But what if: Simple delta rule: …What function should we use for aj?

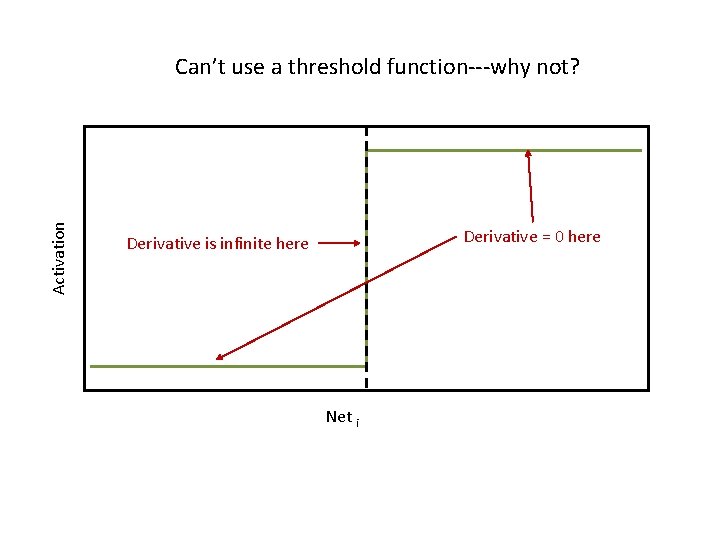
Activation Can’t use a threshold function---why not? Derivative = 0 here Derivative is infinite here Net i

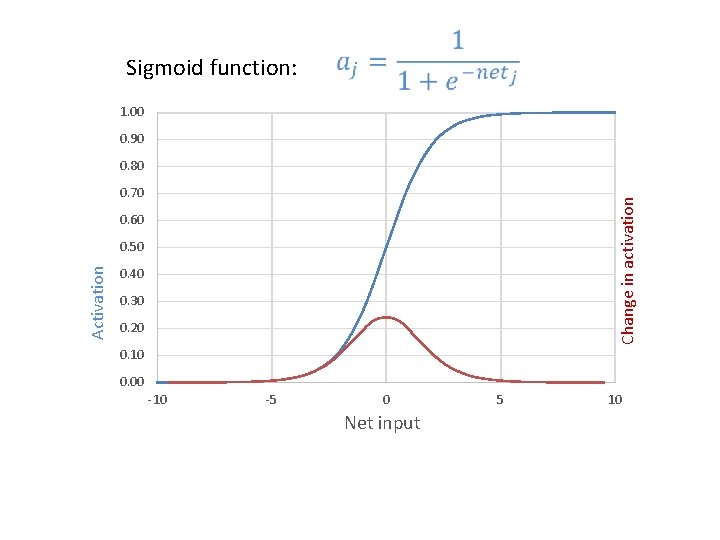
Sigmoid function: 1. 00 0. 90 0. 80 Change in activation 0. 70 0. 60 Activation 0. 50 0. 40 0. 30 0. 20 0. 10 0. 00 -10 -5 0 Net input 5 10

Simple delta rule:

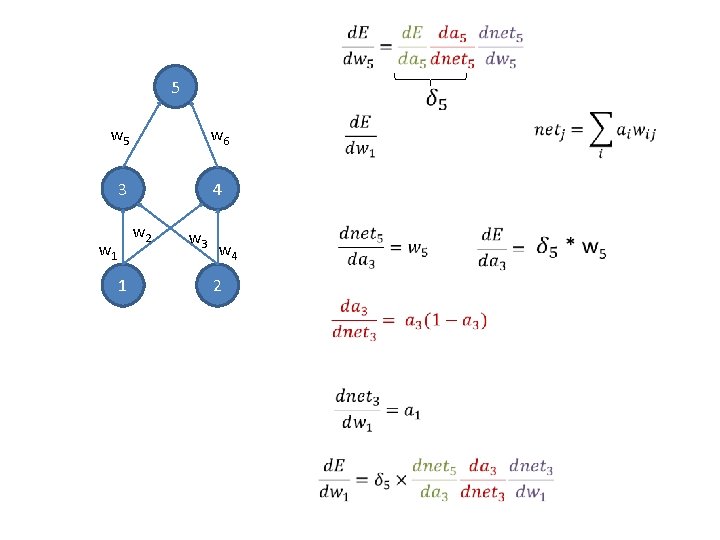
5 w 6 3 4 w 2 w 1 1 w 3 w 4 2

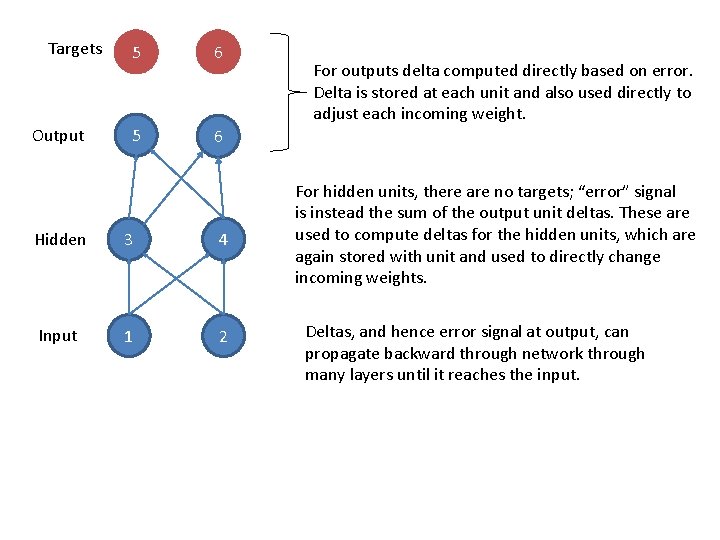
Targets Output 5 6 Hidden 3 4 Input 1 2 For outputs delta computed directly based on error. Delta is stored at each unit and also used directly to adjust each incoming weight. For hidden units, there are no targets; “error” signal is instead the sum of the output unit deltas. These are used to compute deltas for the hidden units, which are again stored with unit and used to directly change incoming weights. Deltas, and hence error signal at output, can propagate backward through network through many layers until it reaches the input.

Alternative error functions.

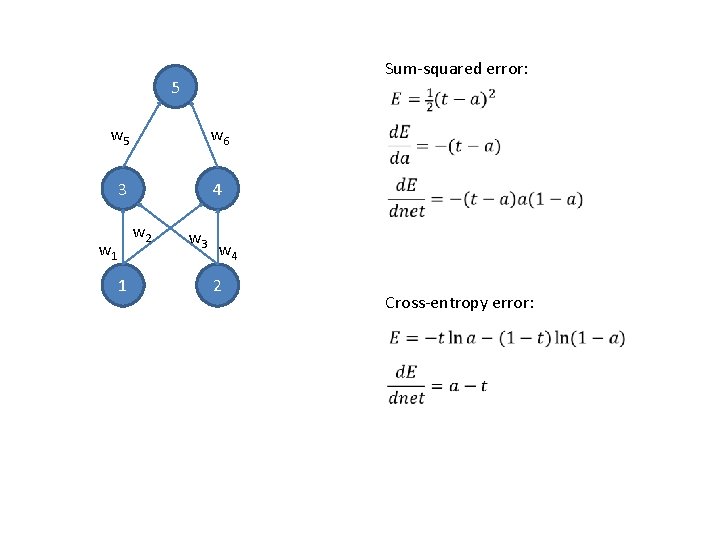
Sum-squared error: 5 w 6 3 4 w 2 w 1 1 w 3 w 4 2 Cross-entropy error:

5 w 6 3 4 w 2 w 1 1 w 3 w 4 2

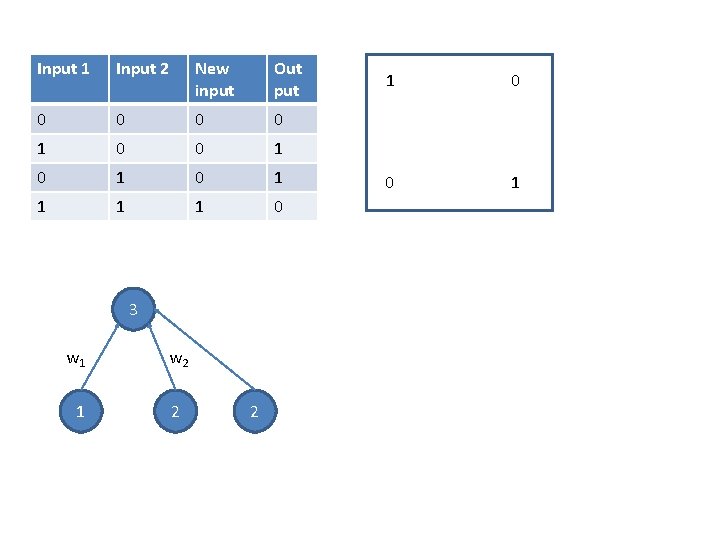
Input 1 Input 2 New input Out put 0 0 1 0 1 1 0 3 w 1 w 2 1 2 2 1 0 0 1