Background Lattices and the LearningwithErrors problem China Summer
Background: Lattices and the Learning-with-Errors problem China Summer School on Lattices and Cryptography, June 2014
Starting Point: Linear Equations � A s b e b
![Learning with Errors (LWE) [R’ 05] � b A s e](http://slidetodoc.com/presentation_image_h2/f2c497bb251c22cc34f62b35c6eda94c/image-3.jpg "Learning with Errors (LWE) [R’ 05] � b A s e")
Learning with Errors (LWE) [R’ 05] � b A s e
![Learning with Errors (LWE) [R’ 05] 1. Is it really hard to solve LWE?](http://slidetodoc.com/presentation_image_h2/f2c497bb251c22cc34f62b35c6eda94c/image-4.jpg "Learning with Errors (LWE) [R’ 05] 1. Is it really hard to solve LWE?")
Learning with Errors (LWE) [R’ 05] 1. Is it really hard to solve LWE? �How hard? �For what range of parameters? 2. Is it useful? �Can we design cryptosystems with security based on the hardness of LWE �We’ll do #2 first, then #1
Using LWE in Cryptography
The Decision-LWE Problem � A b
Search vs. Decision LWE �
Reducing Search to Decision LWE �
Reducing Search to Decision LWE � = +
Reducing Search to Decision LWE � = +
Reducing Search to Decision LWE �
Reducing Search to Decision LWE �
Reducing Search to Decision LWE �
A Useful Variant of LWE �
Uniform- vs. Small-secret LWE �
Uniform- vs. Small-secret LWE �
Uniform- vs. Small-secret LWE = � =
![Regev’s Cryptosystem [R’ 05] �](http://slidetodoc.com/presentation_image_h2/f2c497bb251c22cc34f62b35c6eda94c/image-18.jpg "Regev’s Cryptosystem [R’ 05] �")
Regev’s Cryptosystem [R’ 05] �
![Regev’s Cryptosystem [R’ 05] �](http://slidetodoc.com/presentation_image_h2/f2c497bb251c22cc34f62b35c6eda94c/image-19.jpg "Regev’s Cryptosystem [R’ 05] �")
Regev’s Cryptosystem [R’ 05] �
![Regev’s Cryptosystem [R’ 05] �](http://slidetodoc.com/presentation_image_h2/f2c497bb251c22cc34f62b35c6eda94c/image-20.jpg "Regev’s Cryptosystem [R’ 05] �")
Regev’s Cryptosystem [R’ 05] �
A Useful Variant of the Cryptosystem �
The Hardness of LWE
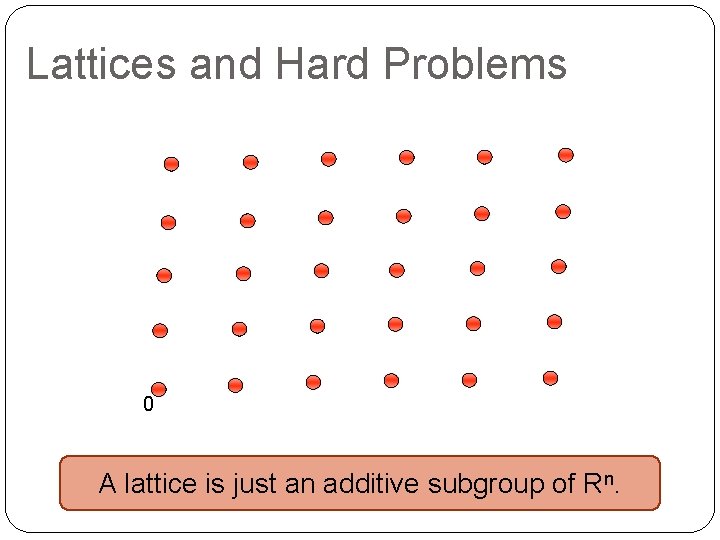
Lattices and Hard Problems 0 A lattice is just an additive subgroup of Rn.
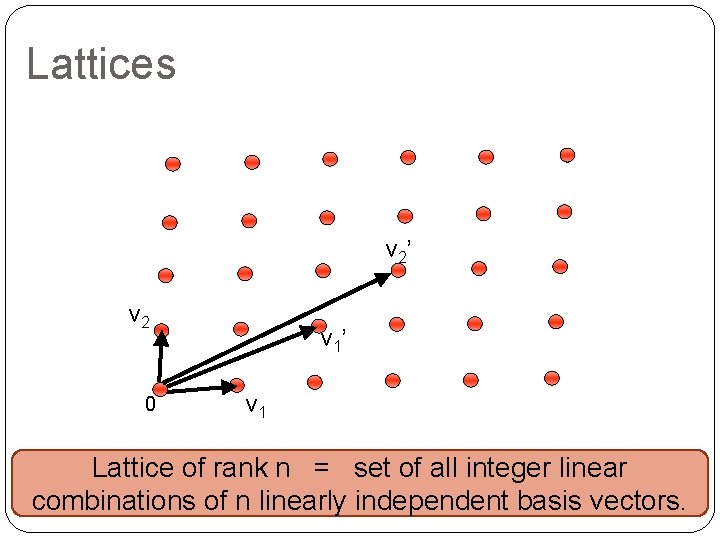
Lattices v 2’ v 2 0 v 1’ v 1 Lattice of rank n = set of all integer linear combinations of n linearly independent basis vectors.
Lattices �
Lattices �
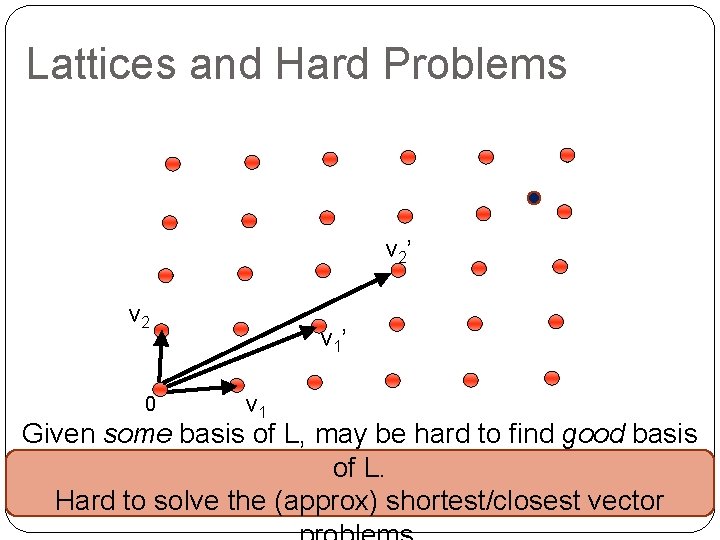
Lattices and Hard Problems v 2’ v 2 0 v 1’ v 1 Given some basis of L, may be hard to find good basis of L. Hard to solve the (approx) shortest/closest vector
Hard Problems �
Hard Problems: What’s Known? �
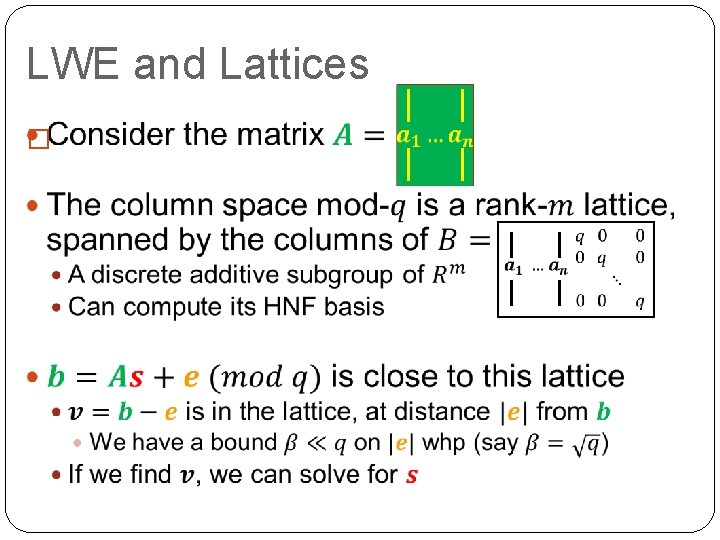
LWE and Lattices �
Bounded Distance Decoding (BDD) �
LWE and Lattices �
Summary �
- Slides: 33