Back to Random Walks on Graphs Random walk

Back to Random Walks on Graphs Random walk on a graph: Stationary distribution:
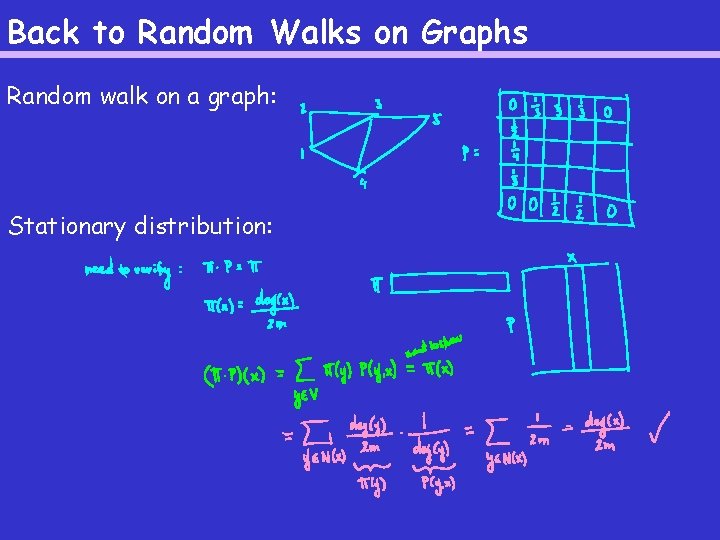
Back to Random Walks on Graphs Random walk on a graph: Stationary distribution:

Detailed balance condition: An ergodic Markov chain satisfying the detailed balance condition is called reversible.

Hitting, Commute, Cover Time Given is a MC M=( , P). Hitting time from u to v, for u, v 2 : hu, v(M) = expected number of steps of M started from u until first reach v

Hitting, Commute, Cover Time Given is a MC M=( , P). Hitting time from u to v, for u, v 2 : hu, v(M) = expected number of steps of M started from u until first reach v Commute time between u and v, for u, v 2 : Cu, v(M) = expected number of steps of M started from u to reach v and get back to u

Hitting, Commute, Cover Time Given is a MC M=( , P). Hitting time from u to v, for u, v 2 : hu, v(M) = expected number of steps of M started from u until first reach v Commute time between u and v, for u, v 2 : Cu, v(M) = expected number of steps of M started from u to reach v and get back to u Cover time: Cu(M) = expected number of steps of M started from u until every state in has been visited at least once C(M) = maxu 2 Cu(M)

Hitting Time of a Random Walk on a Graph Given is a graph G.
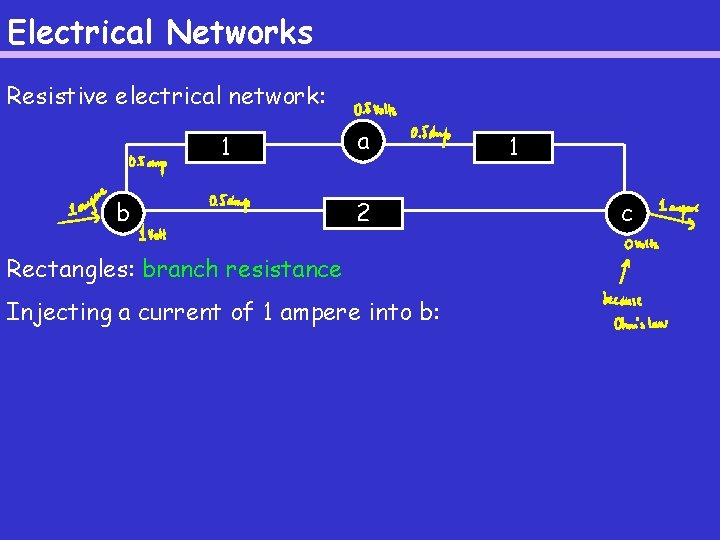
Electrical Networks Resistive electrical network: 1 b a 2 Rectangles: branch resistance Injecting a current of 1 ampere into b: 1 c
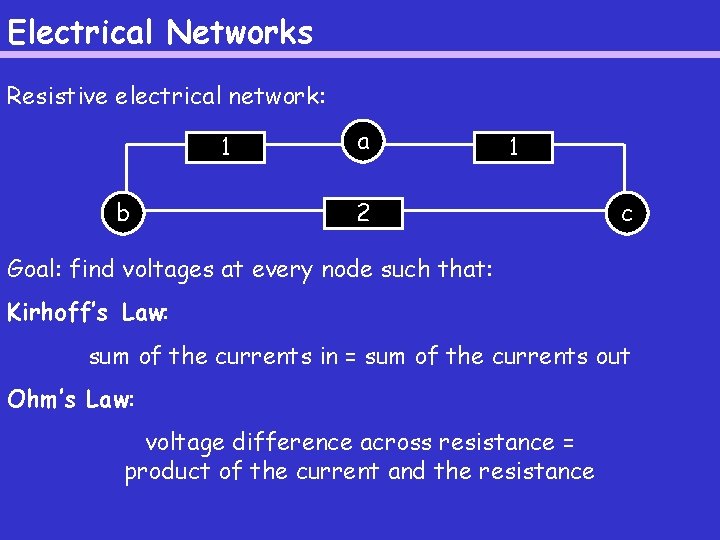
Electrical Networks Resistive electrical network: 1 b a 1 2 c Goal: find voltages at every node such that: Kirhoff’s Law: sum of the currents in = sum of the currents out Ohm’s Law: voltage difference across resistance = product of the current and the resistance
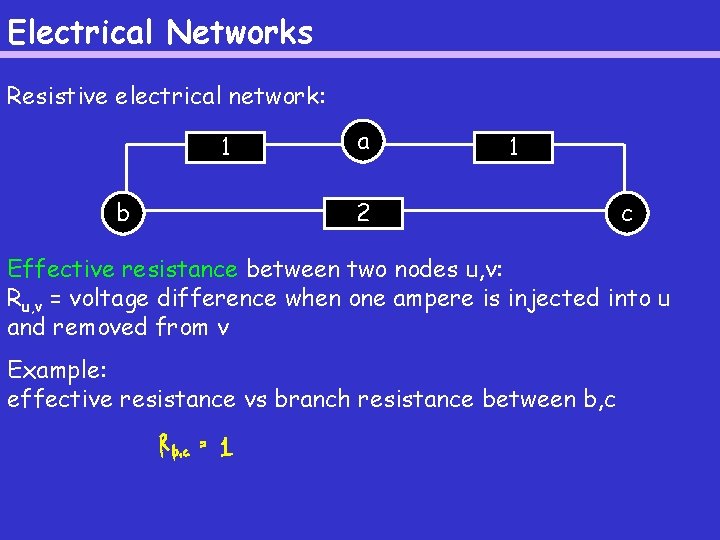
Electrical Networks Resistive electrical network: 1 b a 1 2 c Effective resistance between two nodes u, v: Ru, v = voltage difference when one ampere is injected into u and removed from v Example: effective resistance vs branch resistance between b, c
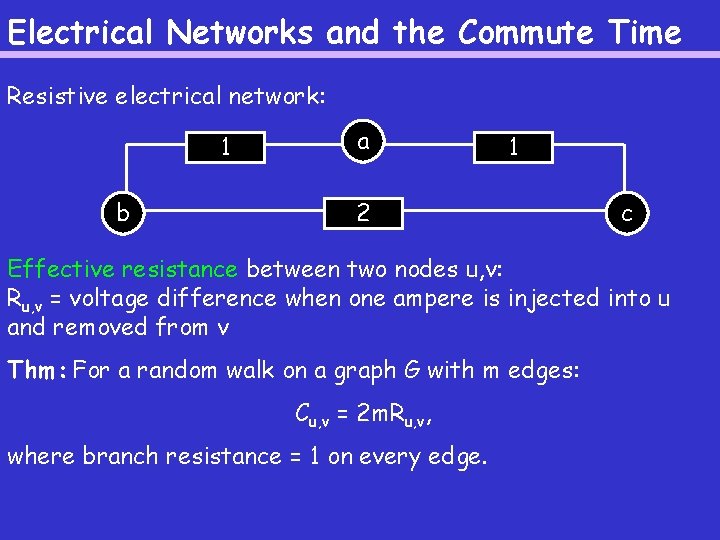
Electrical Networks and the Commute Time Resistive electrical network: 1 b a 1 2 c Effective resistance between two nodes u, v: Ru, v = voltage difference when one ampere is injected into u and removed from v Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v, where branch resistance = 1 on every edge.

Electrical Networks and the Commute Time Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v where branch resistance = 1 for every edge.

Electrical Networks and the Commute Time Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v where branch resistance = 1 for every edge.

Electrical Networks and the Commute Time Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v where branch resistance = 1 for every edge.

Electrical Networks and the Commute Time Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v where branch resistance = 1 for every edge.

Electrical Networks and the Commute Time Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v where branch resistance = 1 for every edge.

Electrical Networks and the Commute Time Thm: For a random walk on a graph G with m edges: Cu, v = 2 m. Ru, v where branch resistance = 1 for every edge. Corollary: For any u, v: Cu, v · n 3.
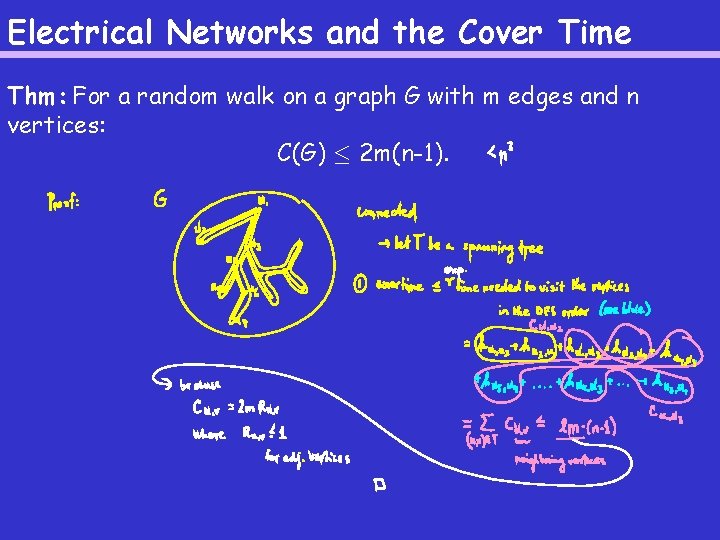
Electrical Networks and the Cover Time Thm: For a random walk on a graph G with m edges and n vertices: C(G) · 2 m(n-1).

Electrical Networks and the Cover Time Thm: For a random walk on a graph G with m edges and n vertices: m. R(G) · C(G) · 2 e 3 m. R(G)ln n + n, where R(G) = maxu, v. Ru, v.
- Slides: 19