BAB 5 Gerak Parabola Gerak Peluru 11272020 1

BAB. 5 Gerak Parabola (Gerak Peluru) 11/27/2020 1

Pendahuluan. Gerak parabola, gerak dengan jejak (lintasan) berupa grafik parabola (konsep ideal). Gerak parabola, gerak dalam bidang (dua dimensi), yaitu bidang yang dibuat oleh percepatan ( ) dan kecepatan ( ) yang membuat sudut. Contoh gerak parabola, gerak yang terjadi dalam medan gravitasi (g). Syarat yang harus dipenuhi agar gerak menjadi grafik parabola adalah: 1. kecepatan gerak (v) tidak terlalu besar. 11/27/2020 2

Lanjutan. 2. nilai percepatan gravitasi bumi (g) tetap. Syarat g tetap, akan dipenuhi jika jangkauan tidak terlalu jauh (tinggi) dari permukaan bumi. 3. kelengkungan bumi dan gesekan udara diabaikan (bumi dianggap bidang datar). Analisis gerak parabola menggunakan koordinat kartesian dua dimensi (x, y). Sudut antara v dengan garis mendatar (sudut ) disebut sudut elevasi (sudut pelemparan). 11/27/2020 3

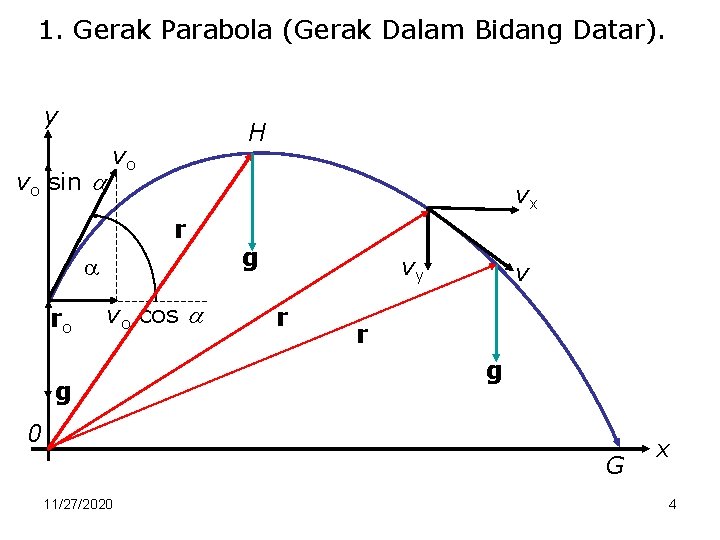
1. Gerak Parabola (Gerak Dalam Bidang Datar). y vo sin H vo vx r ro vo cos g g vy r v r g 0 G 11/27/2020 x 4

Lanjutan. Gerak parabola merupakan paduan (jumlahan) glb (pada sumbu x) dan glbb (pada sumbu y). x = vo cos t t = x/vo cos glb y = vo sin t - ½ g t 2 glbb Mengasilkan y = x tan - ½ g x 2/vo cos 2 atau y = f (x 2), yang menyimpulkan bentuk grafik (lintasan) parabola. 11/27/2020 5

Analisis Gerak Parabola. Kecepatan gerak parabola setiap saat dipenuhi dengan, dv = g dt (dalam hal ini besaran a = g) Jika dihitung kecepatan partikel setiap saat (di titik tertentu) akan diperoleh, v = vo + g t Jika kecepatan gerak partikel dinyatakan dengan komponen vektor maka menjadi, i vx + j vy = i vo cos + j vo sin - g t j Posisi partikel setiap saat dipenuhi dengan, r = r o + v o t + ½ g t 2 11/27/2020 6

Lanjutan. Jika posisi gerak partikel setiap saat dinyatakan dengan komponen vektor maka persm menjadi, i x + j y = yo j + i vo cos t + j vo sin t – ½ g t 2 j Persm posisi dan kecepatan jika dipisahkan maka menjadi, Gerak pada sumbu x, Letak posisi partikel, x = vo cos t Besar kecepatan partikel, vx = vo cos 11/27/2020 7

Lanjutan. Gerak pada sumbu y, Letak posisi partikel, y = yo + vo sin t - ½ g t 2. Besar kecepatan partikel, vy = vo sin t - g t Kecepatan partikel setiap saat, 11/27/2020 8

Lanjutan. y vo sin H vo vx r ro titik tertinggi vo cos g g vy r v r g titik terjauh 0 G 11/27/2020 x 9

Lanjutan. Letak posisi-posisi ekstrim pada gerak parabola Titik tertinggi (H) dijangkau, jika partikel sudah tidak akan naik lagi, maka dipenuhi vy = 0. vy = vo sin - g t. H = 0. Dari persm tersebut, diperoleh waktu terbang (t. H) benda (partikel) untuk mencapai titik H (titik tertinggi) yaitu: 11/27/2020 10

Lanjutan. Koordinat H (x. H, y. H) Kecepatan partikel pada H adalah vo cos . 11/27/2020 11

Koordinat G (titik terjauh partikel jatuh). Titik terjauh, dipenuhi jika partikel sampai di tanah (maka dipenuhi y. G = 0). y. G = g t 2 - 2 vo t sin - 2 yo = 0 Bentuk persm kuadrat dari t. Ada dua nilai memenuhi, dan digunakan yang memenuhi syarat, Koordinat partikel menjadi (vo cos t. G ; 0) Kecepatan partikel, 11/27/2020 12

Contoh. Peluru ditembakkan dari suatu tempat ketinggian 100 m dari permukaan tanah. Peluru vo = 80 m s-1 dengan membuat = 30 o dengan bidang horisontal. Berapa ketinggian maksm yang dicapai peluru tersebut ? Dimana dan dengan kecepatan berapa peluru tersebut jatuh di tanah ? g = 10 m s-2. Penyelesaian. Lihat gambar gerak parabola di depan !. Jika titik tertinggi H, maka koordinat H menjadi 11/27/2020 13

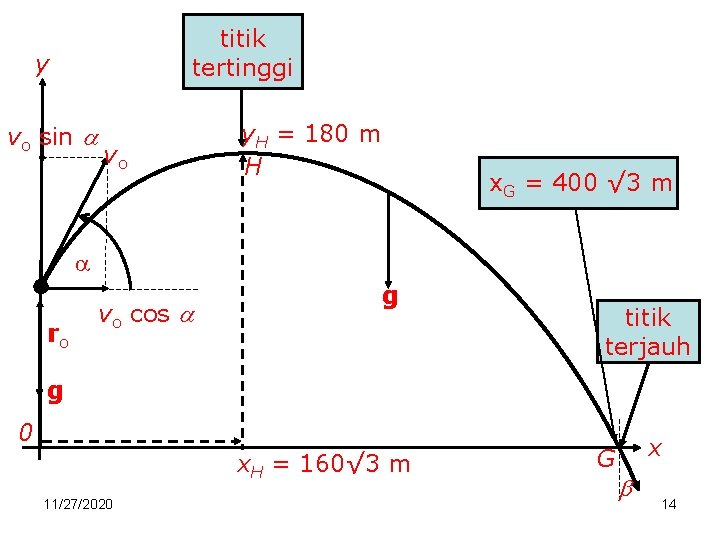
titik tertinggi y vo sin vo y. H = 180 m H x. G = 400 √ 3 m ro vo cos g titik terjauh g 0 x. H = 160√ 3 m 11/27/2020 G x 14

Sambungan. Koordinat titik tertinggi, H (160√ 3; 180) m Peluru jatuh di titik G, maka g t 2 - 2 vo t sin - 2 yo = 10 t 2 – 80 t – 200 = 0 11/27/2020 15

t 2 – 8 t – 20 = 0 (t – 10)(t + 2) = 0 Waktu terbang peluru adalah 10 detik. x. G = vo t. G cos = (80) (10) ½ √ 3 m = 400 √ 3 m Koordinat titik G atau peluru di bumi G (400√ 3; 0) Kecepatan jatuh = ( vo cos )2 + (vo sin - g t. G)2 = (40√ 3)2 + (40 – 100)2 = 4800 + 3600 = 8400 m s -1 Kecepatan partikel menumbuk tanah 20 √ 21 m s-1 ( vo). 11/27/2020 16

Arah kecepatan peluru jatuh di G, tan = vx /vy. tan (40√ 3)/(- 60) = - (2/3)√ 3, = …… Tetapi jika peluru ditembakkan dari permukaan tanah (yo = 0), besar kecepatan dan arah sampai di tanah akan sama dengan saat awal peluru ditembakkan, hanya arahnya yang berlawanan. 11/27/2020 17

Contoh. Dua peluru memiliki jangkauan R membutuhkan waktu t 1 dan t 2 untuk mencapai ketinggian masing-masing. Buktikan t 1 t 2 = 2 R/g ! Penyelesaian. R = v cos t. t = (2 v sin )/g. sin 2 + cos 2 = 1 R g 2 t 2/4 v 2 + R 2/v 2 t 2 = 1 g 2 t 4 – 4 v 2 t 2 + 4 R 2 = 0 x 2 = t 2 g 2 x 2 – 4 v 2 x + 4 R 2 = 0. 11/27/2020 18

11/27/2020 19

2. Gerak Vertikal (Jatuh Bebas) Gerak vertikal ke atas dapat dianggap, sebagai gerak parabola khusus [yaitu sudut elevasi ben-da = 90 o, (nilai cos 90 o = 0 dan sin 90 o = 1)]. Persm gerak peluru tegak lurus, identik gerak lurus vertikal (gerak dalam sb. y). y j = yo j + vo j t + ½ g (- j) t 2 Persm gerak ke atas (tegak lurus) menjadi, y = y o + v o t - ½ g t 2 Persm gerak ke bawah (tegak lurus dihempaskan) menjadi, y = yo + vo t + ½ g t 2 11/27/2020 20

Jika partikel (peluru) dilempar ke atas, maka suatu saat partikel akan mencapai puncak. Partikel akan mencapai puncak dipenuhi v = 0. Jika v = 0, akan dipenuhi vo = g t. Koordinat puncak menjadi, y = yo + Kecepatan partikel, pada suatu posisi setiap saat dinyatakan sebagai, v 2 = vo 2 ± 2 g y. 11/27/2020 21

Contoh. Seorang melempar benda (secara tegak lurus) dengan kecepatan awal 40 m s-1 dari ketinggian 45 m. Berapakah ketinggian yang dicapai benda tersebut dan dengan kecepatan berapa benda akan menumbuk tanah ? g = 10 ms-2. Penyelesaian. Benda mencapai titik tertinggi, y = yo + y = 45 m + (1600/20) m = 125 m. 11/27/2020 22

Kecepatan menumbuk tanah, v 2 = vo 2 + 2 g y. v 2 = (40)2 + 2 (- 10)(- 45) = 1600 + 900 = 2500 m 2 s-2. Besar kecepatan benda menumbuk tanah, v = 50 m s-1, dengan arah ke bawah. 11/27/2020 23

Contoh. Sebuah batu dijatuhkan dari ketinggian h. Se-telah t detik batu kedua dijatuhkan ke bawah dengan diberi kecepatan v. Kedua benda me-ngenai permukaan tanah secara bersamaan. Per-syaratan apa yang diperlukan agar hal tersebut dapat terjadi ? Penyelesaian. Batu pertama, h = ½ g t 12 atau Batu kedua, h = v (t 1 + t) + ½ g (t 1 + t)2. 11/27/2020 24

Persm di atas dikuadratkan dikalikan g menjadi, 11/27/2020 25

8 h (g 2 t 2 + v 2 - 2 v t) = g t 2 (g 2 t 2 + 4 v 2 – 4 v g t) 8 h (g t - v)2 = g t 2 (g t - 2 v)2 11/27/2020 26

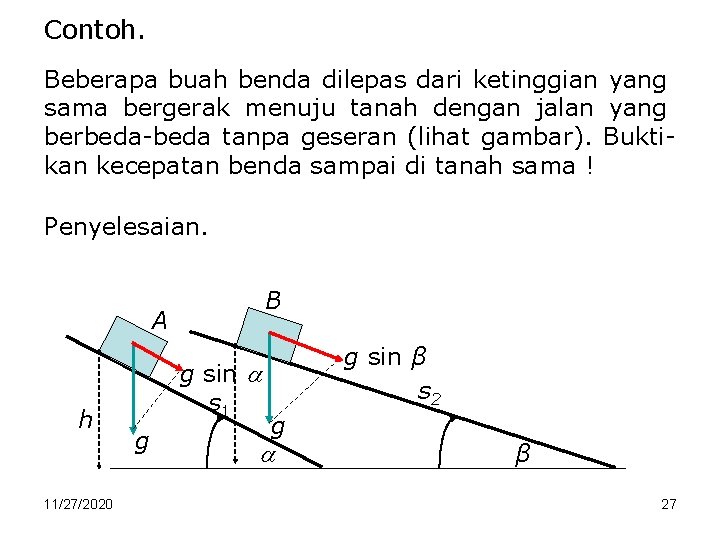
Contoh. Beberapa buah benda dilepas dari ketinggian yang sama bergerak menuju tanah dengan jalan yang berbeda-beda tanpa geseran (lihat gambar). Buktikan kecepatan benda sampai di tanah sama ! Penyelesaian. B A h 11/27/2020 g sin s 1 g g sin β s 2 g β 27

lanjutan. Benda A menempuh jarak s 1 dengan memiliki percepatan g sin dan B, s 2 dengan percepatan g sin β. Persm gerak benda A, mencapai tanah dengan waktu t 1, s 1 = ½ g sin t 12. Dalam hal ini t 1 akan, 11/27/2020 28

lanjutan. Persm gerak benda B mencapai tanah dengan waktu t 2, lintasan ditempuh s 2 = ½ g sin t 2. Dalam hal ini t 2 akan sama dengan, 11/27/2020 29

lanjutan. Kecepatan benda sampai di tanah hanya tergantung pada ketinggian benda (h) dan tidak tergan tung pada jalan atau lintasan. Perhatikan v 1 = v 2, terbukti !. 11/27/2020 30

3. Gerak Parabola Dalam Bidang Miring Gerak parabola dalam bidang miring merupakan gerak parabola dengan sumbu x tidak menunjukkan garis horizontal tetapi miring. Analisis gerakan tersebut identik dengan gerak parabola horizontal [sumbu datar (sb x)] dengan dilakukan transformasi. Sudut β merupakan sudut bidang miring. Bidang miring dijadikan sebagai sumbu x yang baru dan dibuat sumbu y baru (sb. y baru sb. x baru). 11/27/2020 31

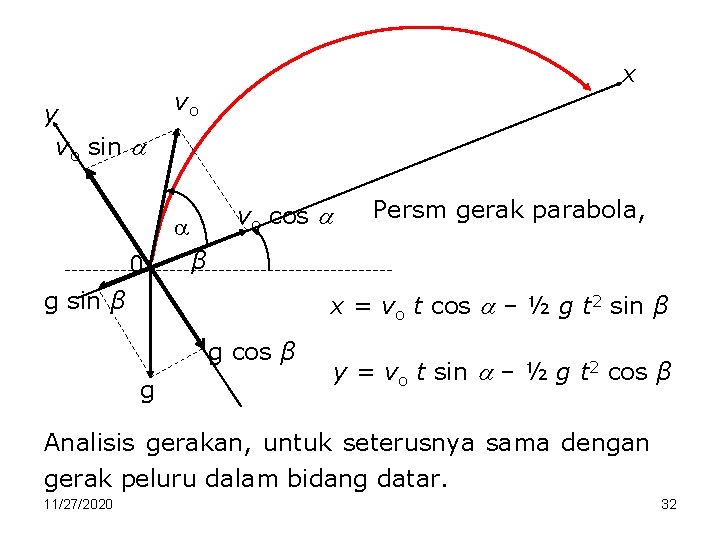
y vo sin vo vo cos 0 x Persm gerak parabola, β g sin β x = vo t cos – ½ g t 2 sin β g cos β g y = vo t sin – ½ g t 2 cos β Analisis gerakan, untuk seterusnya sama dengan gerak peluru dalam bidang datar. 11/27/2020 32

Contoh. Sebuah bola elastis dijatuhkan di atas bidang miring dengan tinggi h. Bola tersebut terpantul dan jatuh pada bidang miring dalam titik yang berbeda dan seterusnya (bola terpantul dan jatuh pada bidang miring dalam posisi yang berbeda), (lihat gambar). Jika jarak antara posisi pertama (1) bola jatuh dan posisi kedua (2), d 12 dan jarak jatuh antara titik kedua (2) dan ketiga (3) adalah d 23. Tentukan perbandingan jarak 11/27/2020 ! 33

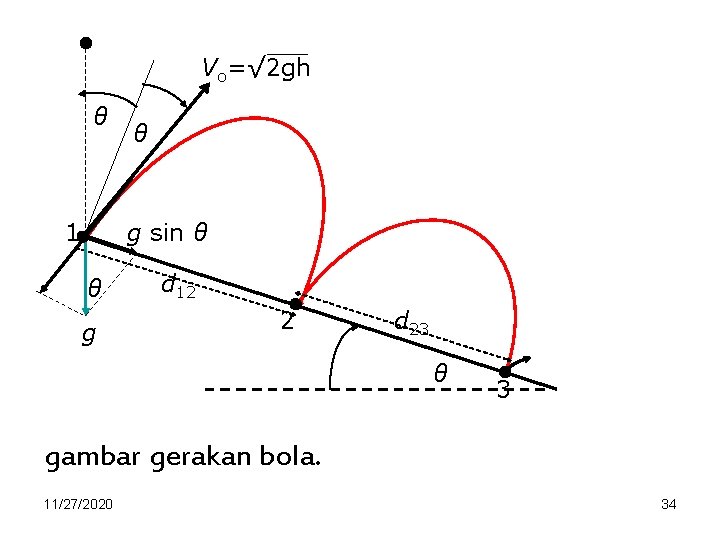
Vo=√ 2 gh θ 1 θ g sin θ θ g d 12 2 d 23 θ 3 gambar gerakan bola. 11/27/2020 34

Kecepatan benda pada posisi (1) vo = √ 2 gh. Persm gerak pada sb. y menjadi, y = vo t cos θ – ½ g t 2 cos θ. Mencapai bidang miring kembali y = 0 sehingga diperlukan waktu t = (2 vo)/g. Jarak tempuh bola jatuh d 12 akan menjadi, d 12 = vo t sin θ + ½ g t 2 sin θ 11/27/2020 35

Besar nilai v adalah benda jatuh pada ketinggian, h + 8 h sin 2 θ atau h (1 + 8 sin 2 θ) Sehingga kecepatan pada posisi (2) menjadi, , nilai tetap. 11/27/2020 36

11/27/2020 37

11/27/2020 38