BAB 4 Peramalan 4 1 Apa itu peramalan

BAB 4 Peramalan 4 -1

Apa itu peramalan? ► ► Proses memprediksi kejadian yang akan datang Sebagai dasar kegiatan bisnis ► Produksi ► Persediaan ► Personalia ► Fasilitas ? ? 4 -2

Time Horizons (Horison Waktu) 1. Peramalan jangka pendek o o 2. Peramalan jangka menengah o o 3. Paling lama 1 tahun, biasanya kurang dari 3 bulan Pembelian, Penjadwalan kerja, tingakt tenaga kerja, penugasan, tingkat produksi 3 bulan sampai 3 tahun Perencanaan penjualan dan produksi, penanggaran (budgeting) Permalan jangka panjang o o 3+ tahun Perencanaan produk baru, lokasi fasilitas, penelitian dan pengembangan 4 -3

Perbedaan horison waktu 1. 2. 3. Peramalan jangka menengah/panjang terkait dengan isu komprehensif dan mendukung keputusan manajemen terkait perencanaan dan produk, pabrik, dan proses Peramalan jangka pendek biasanya menggunakan metodoloti yang berbeda dibandingkan peramalan jangka panjang Peramalan jangka pendek cenderung lebih akurat dibandingkan perencanaan jangka panjang 4 -4

Pengaruh Product Life Cycle Introduction – Growth – Maturity – Decline Pendahuluan dan pertumbuhan membutuhkan prakiraan yang lebih lama daripada kematangan dan kemunduran ► Ketika produk melewati siklus hidup, perkiraan berguna dalam memproyeksikan ► ► Tingkat kepegawaian Tingkat persediaan Kapasitas pabrik 4 -5

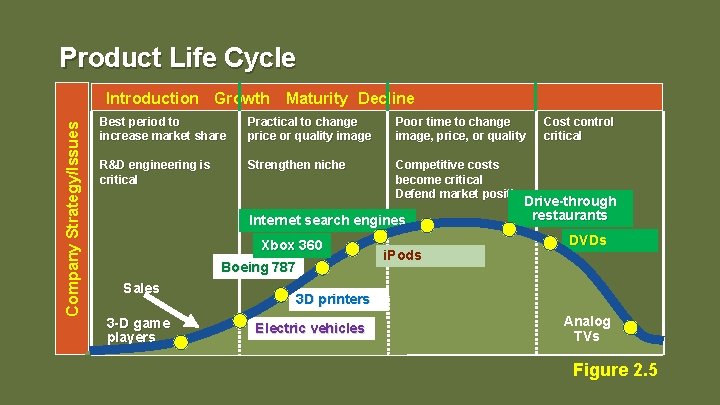
Product Life Cycle Company Strategy/Issues Introduction Growth Maturity Decline Best period to increase market share Practical to change price or quality image Poor time to change image, price, or quality R&D engineering is critical Strengthen niche Competitive costs become critical Defend market position Internet search engines Xbox 360 Boeing 787 Sales 3 -D game players i. Pods Cost control critical Drive-through restaurants DVDs 3 D printers Electric vehicles Analog TVs Figure 2. 5 4 -6

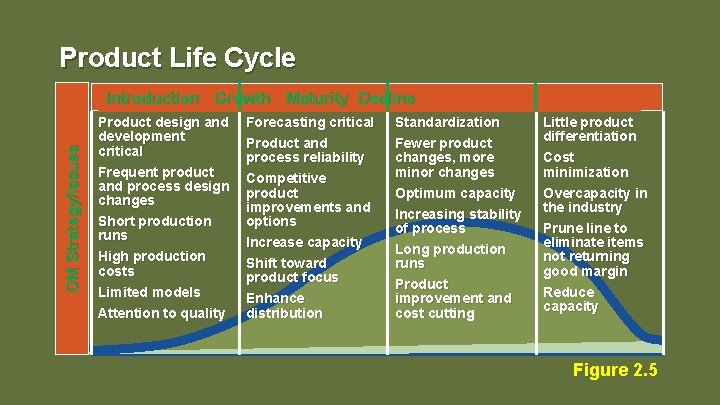
Product Life Cycle OM Strategy/Issues Introduction Growth Maturity Decline Product design and development critical Frequent product and process design changes Short production runs High production costs Limited models Attention to quality Forecasting critical Product and process reliability Competitive product improvements and options Increase capacity Shift toward product focus Enhance distribution Standardization Fewer product changes, more minor changes Optimum capacity Increasing stability of process Long production runs Product improvement and cost cutting Little product differentiation Cost minimization Overcapacity in the industry Prune line to eliminate items not returning good margin Reduce capacity Figure 2. 5 4 -7

Jenis Peramalan 1. Peramalan ekonomi o 2. 3. Diarahkan pada siklus bisnis inflasi, penawaran uang beredar, perumahan, dll Peramalan teknologi o Pemprediksi kemajuan teknologi o Pengaruh kepada produk baru Peramalan permintaan o Memprediksi penjualan dari produk yang ada sekarang 4 -8

Pentingnya Peramalan o Supply-Chain Management – Hubungan pemasok yang baik, keunggulan dalam inovasi produk, biaya dan kecepatan ke pasar o Human Resources – Mempekerjakan, melatih, merumahkan pekerja o Capacity – Kekurangan kapasitas dapat mengakibatkan pengiriman yang tidak dapat diandalkan, kehilangan pelanggan, hilangnya pangsa pasar 4 -9

Tahapan Peramalan 1. 2. 3. 4. 5. 6. 7. Menentukan kegunaan peramalan Memilih item yang diramal Menetapkan waktu horison Memilih model peramalan Mengumpulkan data yang diperlukan untuk membuat peramalan Membuat peramalan Validasi dan menerapkan hasil peramalan 4 - 10

Pendekatan Peramalan Metode Kualitatif o o Digunakan ketika situasi tidak jelas dan hanya ada sedikit data o Produk baru o Teknologi baru Melibatkan intuisi, pengalaman o Misal: meramalkan penjualan di Internet 4 - 14

Pendekatan Peramalan Metode kuantitatif ► ► Digunakan ketika situasi 'stabil' dan data historis tersedia. ► Produk yang sekarang ada ► Teknologi saat ini Melibatkan teknik matematika ► e. g. , Peramalan penjualan tv warna 4 - 15

Metode Kualitatif 1. Jury of Executive Opinion ► 2. Menggabungkan pendapat ahli-tingkat-tinggi, kadang-kadang ditambah dengan model statistik Delphi method ► Panel ahli, bertanya secara berulang 4 - 16

Metode Kualitatif 3. Sales Force Composite ► 3. Perkiraan dari penjual individu ditinjau untuk masuk akal, kemudian dikumpulkan Market Survey ► Tanyakan kepada pelanggan 4 - 17

Jury of Executive Opinion o Melibatkan sekelompok kecil ahli dan manajer tingkat tinggi o Kelompok memperkirakan permintaan dengan bekerja sama o Menggabungkan pengalaman manajerial dengan model statistik o Relatif cepat o ‘Group-think’ disadvantage 4 - 18

Delphi Method ► ► Proses grup berulang, berlanjut hingga konsensus tercapai 3 jenis peserta ► Pembuat keputusan ► Staf ► Responden Decision Makers (Evaluate responses and make decisions) Staff (Administering survey) Respondents (People who can make valuable judgments) 4 - 19

Sales Force Composite o o Setiap salesperson memproyeksikan penjualannya Dikombinasikan di tingkat kabupaten dan nasional Staf penjualan tahu keinginan pelanggan Mungkin terlalu optimis 4 - 20

Market Survey o o Tanyakan kepada pelanggan tentang rencana pembelian Berguna untuk desain dan perencanaan permintaan dan produk Apa yang dikatakan konsumen, dan apa yang sebenarnya mereka lakukan mungkin berbeda Mungkin terlalu optimis 4 - 21

Pendekatan Kuantitatif untuk Peramalan 4 - 22

Sekilas Pendekatan Kuantitatif 1. 2. 3. 4. 5. Naive approach (Pendekatan naif) Moving averages (Rata 2 bergerak) Exponential smoothing (pemulusan eksponensial) Trend projection (proyeksi tren / kecenderungan) Linear regression (regresi linier) Model Runtut Waktu Model Asosiatif 4 - 23

TIME SERIES MODEL 4 - 24

Peramalan Time-Series v Sekumpulan Data Numerik dengan jarak waktu sama v v Diperoleh dengan mengamati variabel respon pada periode waktu yang teratur Prakiraan hanya berdasarkan nilai lampau, tidak ada variabel lain yang penting v Asumsikan bahwa faktor-faktor yang mempengaruhi masa lalu dan sekarang akan terus mempengaruhi di masa depan 4 - 25

Komponen Time-Series Trend Seasonal (Musiman) Cyclical (Siklus) Random (Acak) 4 - 27

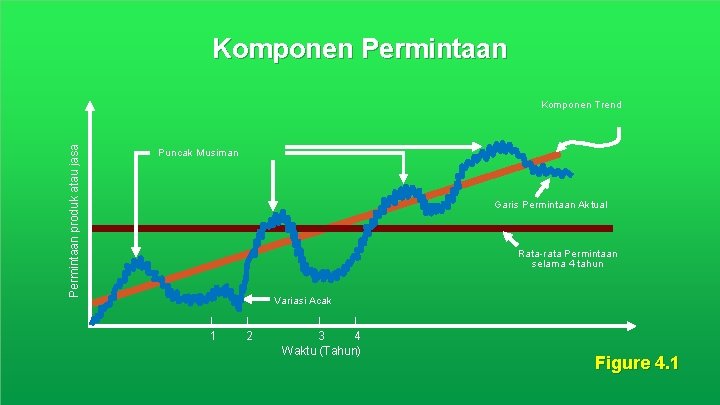
Komponen Permintaan produk atau jasa Komponen Trend Puncak Musiman Garis Permintaan Aktual Rata-rata Permintaan selama 4 tahun Variasi Acak | 1 | 2 | | 3 4 Waktu (Tahun) Figure 4. 1 4 - 28

Komponen Trend (Kecenderungan) q Persisten (stabil), seluruhnya berpola ke atas atau ke bawah q Perubahan karena populasi, teknologi, usia, budaya, dll. q Biasanya beberapa tahun lamanya 4 - 29

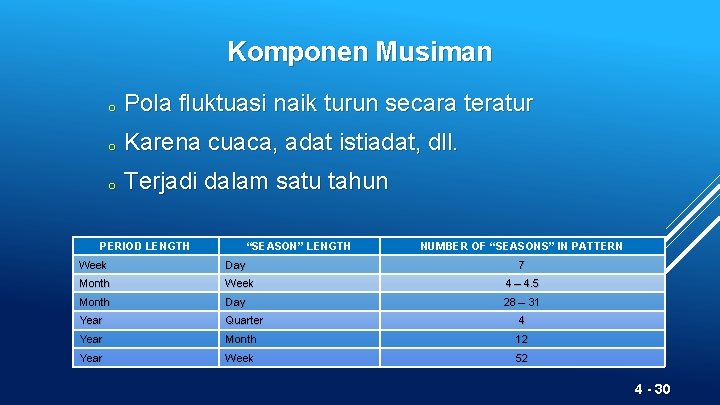
Komponen Musiman o Pola fluktuasi naik turun secara teratur o Karena cuaca, adat istiadat, dll. o Terjadi dalam satu tahun PERIOD LENGTH “SEASON” LENGTH NUMBER OF “SEASONS” IN PATTERN Week Day 7 Month Week 4 – 4. 5 Month Day 28 – 31 Year Quarter 4 Year Month 12 Year Week 52 4 - 30

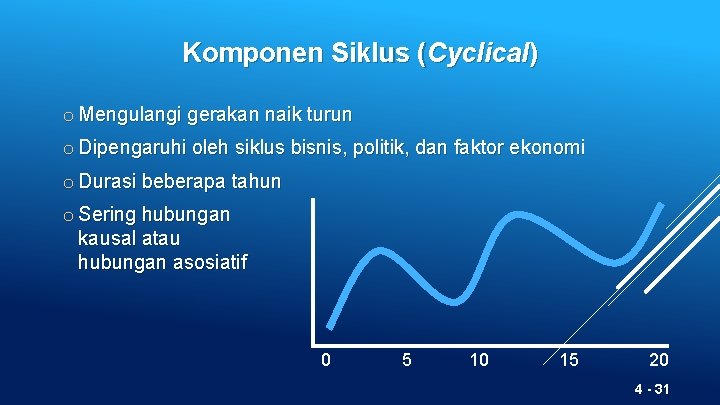
Komponen Siklus (Cyclical) o Mengulangi gerakan naik turun o Dipengaruhi oleh siklus bisnis, politik, dan faktor ekonomi o Durasi beberapa tahun o Sering hubungan kausal atau hubungan asosiatif 0 5 10 15 20 4 - 31

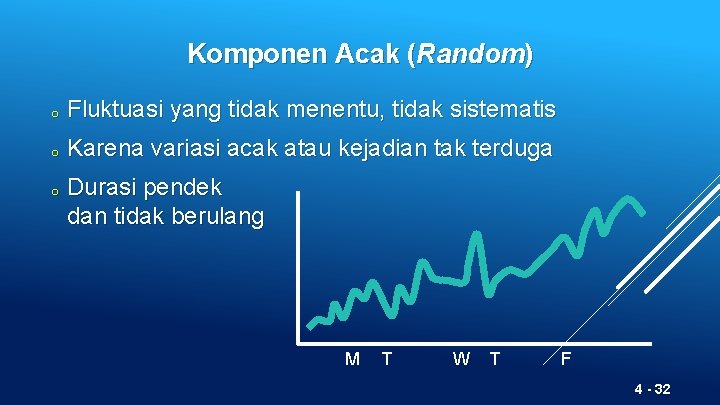
Komponen Acak (Random) o Fluktuasi yang tidak menentu, tidak sistematis o Karena variasi acak atau kejadian tak terduga o Durasi pendek dan tidak berulang M T W T F 4 - 32

1. NAIVE APPROACH 4 - 33

Naive Approach (Pendekatan Naif) o Menganggap permintaan periode yad sama dengan permintaan masa lampau o contoh. , Jika pada bulan Januari permintaan sebesar 68, maka bulan Februari juga sebesar 68 o Metode ini lebih efektif dan efisien o Dapat digunakan sebagai titik awal yang baik 4 - 34

2. METODE RATA BERGERAK 4 - 35

Moving Average Method o MA adalah sekumpulan rata-rata hitung o Digunakan jika tidak ada atau sedikit tren o Sering digunakan untuk pemulusan ü Provides overall impression of data over time 4 - 36

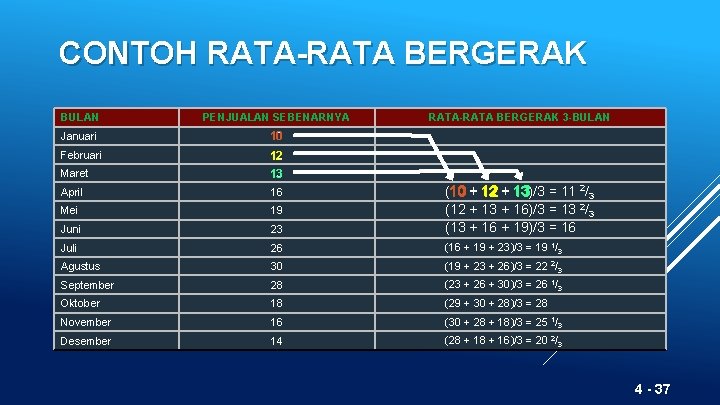
CONTOH RATA-RATA BERGERAK BULAN PENJUALAN SEBENARNYA RATA-RATA BERGERAK 3 -BULAN Januari 10 10 Februari 12 12 Maret 13 April 16 Mei 19 Juni 23 2/ (10 + 12 + 13)/3 = 11 10 + 12 + 13 3 2 (12 + 13 + 16)/3 = 13 /3 (13 + 16 + 19)/3 = 16 Juli 26 (16 + 19 + 23)/3 = 19 1/3 Agustus 30 (19 + 23 + 26)/3 = 22 2/3 September 28 (23 + 26 + 30)/3 = 26 1/3 Oktober 18 (29 + 30 + 28)/3 = 28 November 16 (30 + 28 + 18)/3 = 25 1/3 Desember 14 (28 + 16)/3 = 20 2/3 4 - 37

WEIGHTED MOVING AVERAGE 4 - 38

Rata-rata bergerak tertimbang o Digunakan jika terjadi beberapa kecenderungan (tren) o o Menganggap data masa lampu dianggap kurang penting dibanding data terbaru Bobot didasarkan pada pengalaman dan intuisi (filling) Rata-rata bergerak tertimbang 4 - 39

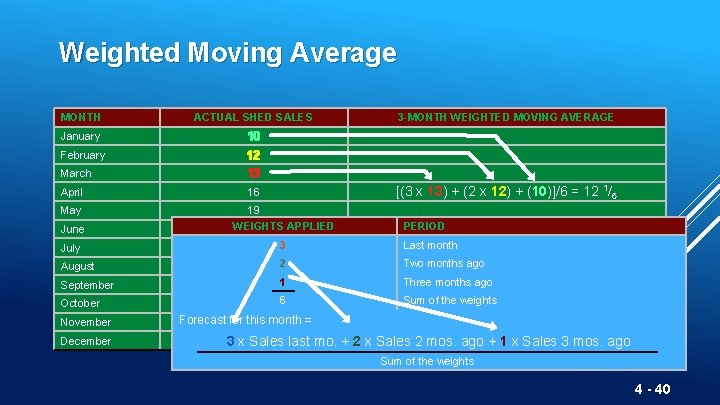
Weighted Moving Average MONTH ACTUAL SHED SALES January 10 February March 12 13 April 16 May June 3 -MONTH WEIGHTED MOVING AVERAGE [(3 x 13) + (2 x 12) + (10)]/6 = 12 1/6 19 WEIGHTS APPLIED 23 PERIOD July 26 3 Last month August 30 2 Two months ago September 28 1 Three months ago October 18 6 Sum of the weights November December Forecast for this month = 16 14 3 x Sales last mo. + 2 x Sales 2 mos. ago + 1 x Sales 3 mos. ago Sum of the weights 4 - 40

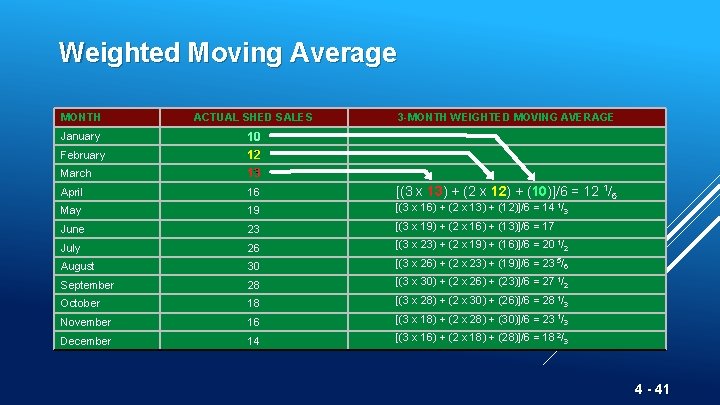
Weighted Moving Average MONTH ACTUAL SHED SALES January March 10 12 13 April 16 May 19 [(3 x 16) + (2 x 13) + (12)]/6 = 14 1/3 June 23 [(3 x 19) + (2 x 16) + (13)]/6 = 17 July 26 [(3 x 23) + (2 x 19) + (16)]/6 = 20 1/2 August 30 [(3 x 26) + (2 x 23) + (19)]/6 = 23 5/6 September 28 [(3 x 30) + (2 x 26) + (23)]/6 = 27 1/2 October 18 [(3 x 28) + (2 x 30) + (26)]/6 = 28 1/3 November 16 [(3 x 18) + (2 x 28) + (30)]/6 = 23 1/3 December 14 [(3 x 16) + (2 x 18) + (28)]/6 = 18 2/3 February 3 -MONTH WEIGHTED MOVING AVERAGE [(3 x 13) + (2 x 12) + (10)]/6 = 12 1/6 4 - 41

Potensi Masalah dengan Moving Average o Meningkatkan n memperhalus ramalan tetapi membuatnya kurang sensitif terhadap perubahan o Tidak meramalkan tren dengan baik o Membutuhkan data historis yang luas 4 - 42

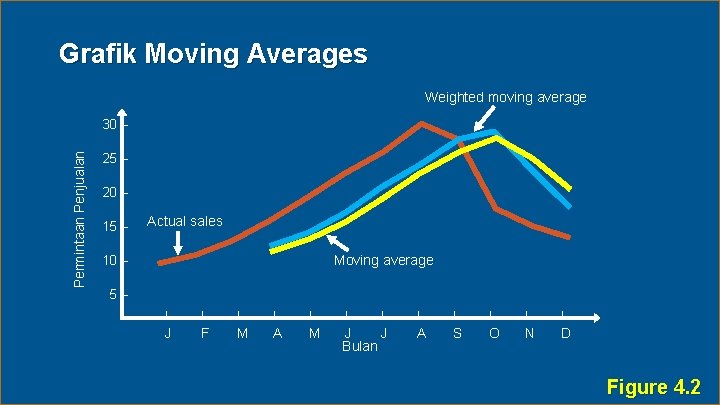
Grafik Moving Averages Weighted moving average Permintaan Penjualan 30 – 25 – 20 – 15 – Actual sales Moving average 10 – 5 – | | | | J F M A M J J Bulan | | | A S O N D 4 - 43 4. 2 Figure

3. EXPONENTIAL SMOOTHING 4 - 44

Exponential Smoothing q q q Bentuk dari weighted moving average q Bobot turun secara eksponensial q Data sekarang diberi bobot lebih tinggi Diperlukan smoothing constant ( ) q Berkisar dari 0 hingga 1 q Dipilih secara subjektif Memerlukan sedikit catatan data masa lalu 4 - 45

Exponential Smoothing Ramalan baru = Ramalan periode lalu + (Permintaan actual periode lalu – Ramalan periode lalu) F t = F t – 1 + (A t – 1 - F t – 1 ) Di mana Ft = ramalan baru Ft – 1 = ramalan periode sebelumnya = At – 1 = smoothing (atau bobot) constant (0 ≤ ≤ 1) permintaan actual perode sebelumnya 4 - 46

Contoh Exponential Smoothing Permintaan diperkirakan = 142 Ford Mustangs Permintaan aktual = 153 Smoothing constant =. 20 4 - 47

Contoh Exponential Smoothing Permintaan diperkirakan = 142 Ford Mustangs Permintaan aktual = 153 Smoothing constant =. 20 Ramalan baru = 142 +. 2(153 – 142) 4 - 48

Contoh Exponential Smoothing Permintaan diperkirakan = 142 Ford Mustangs Permintaan aktual = 153 Smoothing constant =. 20 Ramalan baru = 142 +. 2(153 – 142) = 142 + 2. 2 = 144. 2 ≈ 144 mobil 4 - 49

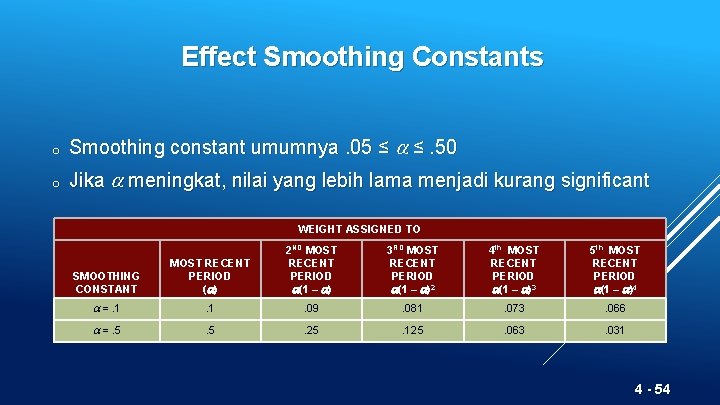
Effect Smoothing Constants o Smoothing constant umumnya. 05 ≤ ≤. 50 o Jika meningkat, nilai yang lebih lama menjadi kurang significant WEIGHT ASSIGNED TO SMOOTHING CONSTANT MOST RECENT PERIOD ( ) 2 ND MOST RECENT PERIOD (1 – ) 3 RD MOST RECENT PERIOD (1 – )2 4 th MOST RECENT PERIOD (1 – )3 5 th MOST RECENT PERIOD (1 – )4 =. 1 . 09 . 081 . 073 . 066 =. 5 . 25 . 125 . 063 . 031 4 - 54

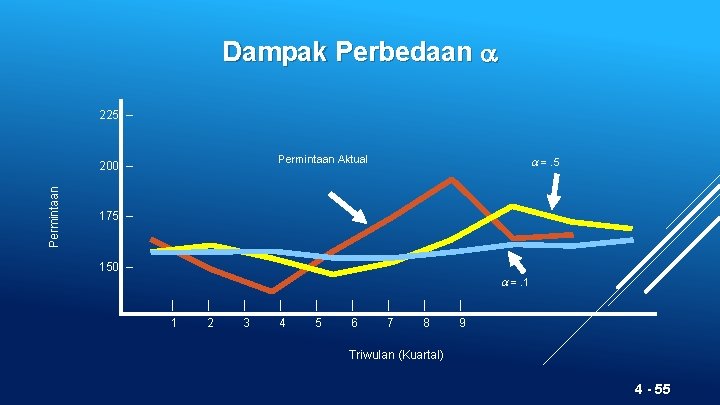
Dampak Perbedaan 225 – Permintaan Aktual Permintaan 200 – =. 5 175 – 150 – =. 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 Triwulan (Kuartal) 4 - 55

Dampak Perbedaan 225 – o Permintaan 200 – 175 – o 150 – Memilih nilai tinggi ketika rata. Permintaan Aktual rata yang mendasarinya cenderung berubah =. 5 Memilih nilai jika rata-rata yang mendasari stabil =. 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 Triwulan (Kuartal) 4 - 56

Memilih Tujuannya adalah untuk mencari ramalan yang paling akurat tidak peduli tekniknya Kita biasanya melakukannya dengan memilih model yang memberi kita kesalahan ramalan terendah Kesalahan Ramalan = Permintaan aktual – Nilai ramalan = At – Ft 4 - 58

PENGUKURAN KESALAHAN YANG UMUM DIGUNAKAN 4 - 60

Ukuran umum tingkat kesalahan 1. 2. 3. Mean Absolute Deviation (MAD) Mean Square Error (MSE) Mean Absolute Percent Error (MAPE) 4 - 61

Ukuran umum tingkat kesalahan 1) Mean Absolute Deviation (MAD) 4 - 62

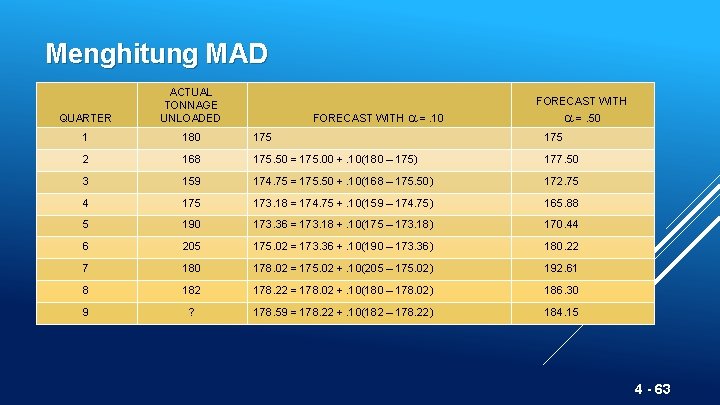
Menghitung MAD QUARTER ACTUAL TONNAGE UNLOADED 1 180 175 2 168 175. 50 = 175. 00 +. 10(180 – 175) 177. 50 3 159 174. 75 = 175. 50 +. 10(168 – 175. 50) 172. 75 4 175 173. 18 = 174. 75 +. 10(159 – 174. 75) 165. 88 5 190 173. 36 = 173. 18 +. 10(175 – 173. 18) 170. 44 6 205 175. 02 = 173. 36 +. 10(190 – 173. 36) 180. 22 7 180 178. 02 = 175. 02 +. 10(205 – 175. 02) 192. 61 8 182 178. 22 = 178. 02 +. 10(180 – 178. 02) 186. 30 9 ? 178. 59 = 178. 22 +. 10(182 – 178. 22) 184. 15 FORECAST WITH =. 10 FORECAST WITH =. 50 4 - 63

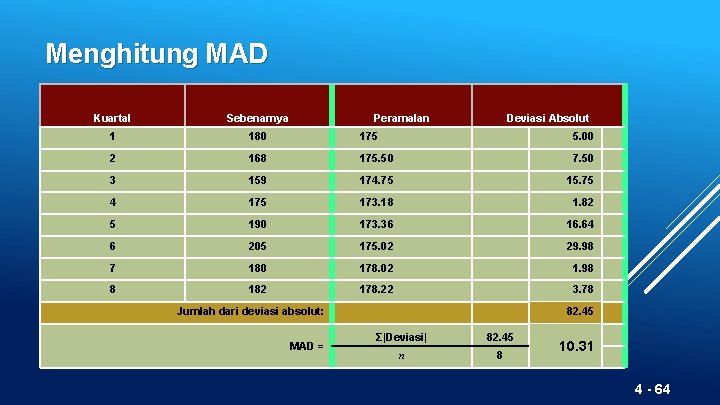
Menghitung MAD Kuartal Sebenarnya Peramalan Deviasi Absolut 1 180 175 5. 00 2 168 175. 50 7. 50 3 159 174. 75 15. 75 4 175 173. 18 1. 82 5 190 173. 36 16. 64 6 205 175. 02 29. 98 7 180 178. 02 1. 98 8 182 178. 22 3. 78 Jumlah dari deviasi absolut: MAD = 82. 45 Σ|Deviasi| 82. 45 n 8 10. 31 4 - 64

Ukuran umum tingkat kesalahan 2) Mean Squared Error (MSE) 4 - 65

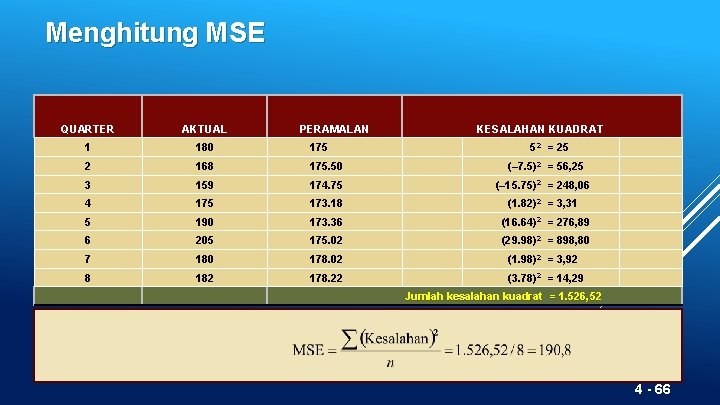
Menghitung MSE QUARTER AKTUAL PERAMALAN KESALAHAN KUADRAT 1 180 175 2 168 175. 50 (– 7. 5)2 = 56, 25 3 159 174. 75 (– 15. 75)2 = 248, 06 4 175 173. 18 (1. 82)2 = 3, 31 5 190 173. 36 (16. 64)2 = 276, 89 6 205 175. 02 (29. 98)2 = 898, 80 7 180 178. 02 (1. 98)2 = 3, 92 8 182 178. 22 (3. 78)2 = 14, 29 52 = 25 Jumlah kesalahan kuadrat = 1. 526, 52 4 - 66

Ukuran umum tingkat kesalahan 3) Mean Absolute Percent Error (MAPE) 4 - 67

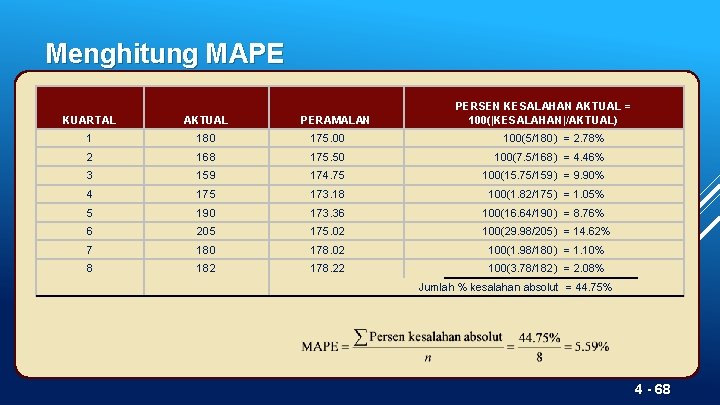
Menghitung MAPE PERAMALAN PERSEN KESALAHAN AKTUAL = 100(|KESALAHAN|/AKTUAL) KUARTAL AKTUAL 1 180 175. 00 100(5/180) = 2. 78% 2 168 175. 50 100(7. 5/168) = 4. 46% 3 159 174. 75 100(15. 75/159) = 9. 90% 4 175 173. 18 100(1. 82/175) = 1. 05% 5 190 173. 36 100(16. 64/190) = 8. 76% 6 205 175. 02 100(29. 98/205) = 14. 62% 7 180 178. 02 100(1. 98/180) = 1. 10% 8 182 178. 22 100(3. 78/182) = 2. 08% Jumlah % kesalahan absolut = 44. 75% 4 - 68

PERBANDINGAN KESALAHAN PERAMALAN MAD vs MSE vs MAPE 4 - 69

Perbandingan Kesalahan Peramalan Rounded Actual Forecast Tonnage with Kuartal Unloaded 1 2 3 4 5 6 7 8 180 168 159 175 190 205 180 182 Absolute Deviation for with =. 10 Rounded Forecast for =. 10 175 5. 00 175. 57. 50 177. 50 9. 50 174. 75 15. 75172. 75 173. 18 1. 82 165. 88 173. 36 16. 64170. 44 175. 02 29. 98180. 22 178. 02 1. 98 192. 61 178. 22 3. 78 186. 30 82. 45 98. 62 Absolute Deviation =. 50 13. 75 9. 12 19. 56 24. 78 12. 61 4. 30 4 - 70

Comparison of Forecast Error Rounded Actual Forecast Tonnage with Quarter Unloaded MAD = 1 2 3 4 5 6 7 8 For =. 10 ∑ |deviations| Rounded Forecast nfor =. 10 Absolute Deviation for with =. 10 Absolute Deviation =. 50 180 175 5. 00 168 175. 57. 50= 82. 45/8 = 10. 31 177. 50 9. 50 159 174. 75 15. 75172. 75 13. 75 175 =. 50 173. 18 1. 82 165. 88 9. 12 For 190 173. 36 16. 64170. 44 19. 56 205 175. 02 = 98. 62/8 = 12. 33 29. 98180. 22 24. 78 180 178. 02 1. 98 192. 61 182 178. 22 3. 78 186. 30 4. 30 82. 45 98. 62 MAD 10. 31 =. 50 12. 33 4 - 71

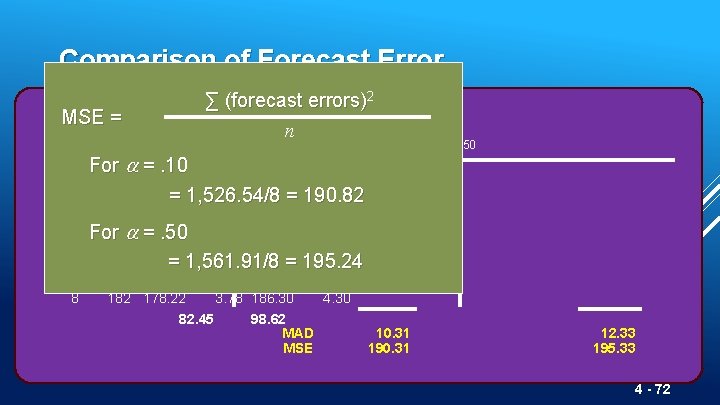
Comparison of Forecast Error 2 ∑ (forecast errors) Absolute Rounded Absolute Deviation Forecast Deviation for with nfor Rounded Actual Forecast Tonnage with Quarter Unloaded MSE = 1 2 3 4 5 6 7 8 =. 10 For =. 10 180 175 5. 00 = 1, 526. 54/8 = 190. 82 168 175. 57. 50 177. 50 9. 50 =. 50 159 174. 75 15. 75172. 75 13. 75 175 =. 50 173. 18 1. 82 165. 88 9. 12 For 190 173. 36 16. 64170. 44 19. 56 = 1, 561. 91/8 = 195. 24 205 175. 02 29. 98180. 22 24. 78 180 178. 02 1. 98 192. 61 182 178. 22 3. 78 186. 30 4. 30 82. 45 98. 62 MAD 10. 31 MSE 190. 31 =. 50 12. 33 195. 33 4 - 72

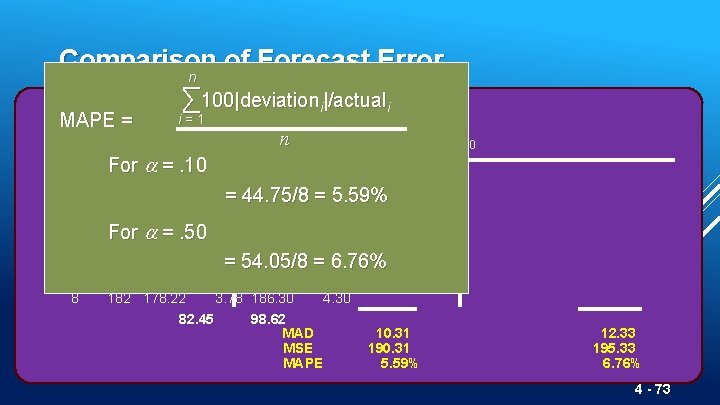
Comparison of Forecast Error n ∑ 100|deviation i|/actual i Rounded Absolute i = 1 Actual Forecast MAPE = Tonnage with Quarter 1 2 3 4 5 6 7 8 Unloaded For =. 10 Deviation for with =. 10 n Forecast for =. 10 Deviation =. 50 180 175 5. 00 = 44. 75/8 = 5. 59% 168 175. 57. 50 177. 50 9. 50 159 174. 75 15. 75172. 75 13. 75 175 For 173. 18 =. 50 1. 82 165. 88 9. 12 190 173. 36 16. 64170. 44 19. 56 = 54. 05/8 = 6. 76% 205 175. 02 29. 98180. 22 24. 78 180 178. 02 1. 98 192. 61 182 178. 22 3. 78 186. 30 4. 30 82. 45 98. 62 MAD 10. 31 MSE 190. 31 MAPE 5. 59% =. 50 12. 33 195. 33 6. 76% 4 - 73

Comparison of Forecast Error Rounded Actual Forecast Tonnage with Quarter Unloaded 1 2 3 4 5 6 7 8 180 168 159 175 190 205 180 182 Absolute Deviation for with =. 10 Rounded Forecast for =. 10 Absolute Deviation =. 50 175 5. 00 175. 57. 50 177. 50 9. 50 174. 75 15. 75172. 75 13. 75 173. 18 1. 82 165. 88 9. 12 173. 36 16. 64170. 44 19. 56 175. 02 29. 98180. 22 24. 78 178. 02 1. 98 192. 61 178. 22 3. 78 186. 30 4. 30 82. 45 98. 62 MAD 10. 31 MSE 190. 31 MAPE 5. 59% =. 50 12. 33 195. 33 6. 76% 4 - 74

EXPONENTIAL SMOOTHING WITH TREND ADJUSTMENT 4 - 75

Exponential Smoothing with Trend Adjustment When a trend is present, exponential smoothing must be modified MONTH ACTUAL DEMAND FORECAST (Ft) FOR MONTHS 1 – 5 1 100 Ft = 100 (given) 2 200 Ft = F 1 + (A 1 – F 1) = 100 +. 4(100 – 100) = 100 3 300 Ft = F 2 + (A 2 – F 2) = 100 +. 4(200 – 100) = 140 4 400 Ft = F 3 + (A 3 – F 3) = 140 +. 4(300 – 140) = 204 5 500 Ft = F 4 + (A 4 – F 4) = 204 +. 4(400 – 204) = 282 4 - 76

Exponential Smoothing with Trend Adjustment Forecast including (FITt) trend = Exponentially smoothed forecast trend Exponentially (Ft) + smoothed (Tt) Ft = (At - 1) + (1 - )(Ft - 1 + Tt - 1) Tt = b(Ft - 1) + (1 - b)Tt - 1 where Ft = exponentially smoothed forecast average Tt = exponentially smoothed trend At = actual demand = smoothing constant for average (0 ≤ ≤ 1) b = smoothing constant for trend (0 ≤ b ≤ 1) 4 - 77

Exponential Smoothing with Trend Adjustment Step 1: Compute Ft Step 2: Compute Tt Step 3: Calculate the forecast FITt = Ft + Tt 4 - 78

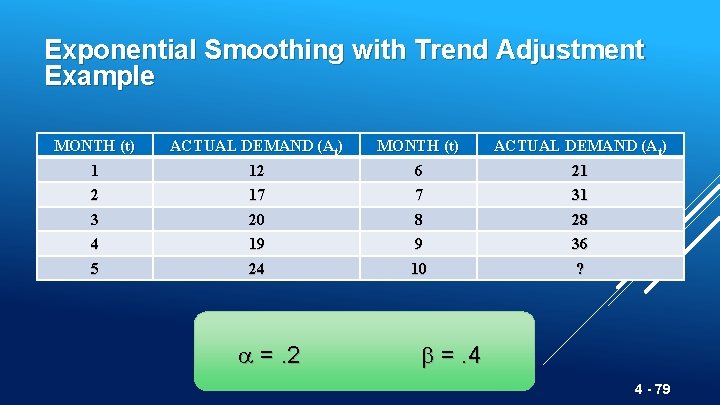
Exponential Smoothing with Trend Adjustment Example MONTH (t) 1 ACTUAL DEMAND (At) 12 MONTH (t) 6 ACTUAL DEMAND (At) 21 2 3 17 20 7 8 31 28 4 5 19 24 9 10 36 ? =. 2 b =. 4 4 - 79

Exponential Smoothing with Trend Adjustment Example TABLE 4. 1 Forecast with -. 2 and b =. 4 SMOOTHED FORECAST AVERAGE, Ft MONTH ACTUAL DEMAND 1 12 11 2 17 12. 80 3 20 4 19 5 24 6 21 7 31 8 28 9 36 10 — SMOOTHED TREND, Tt FORECAST INCLUDING TREND, FITt 2 13. 00 Step 1: Average for Month 2 F 2 = A 1 + (1 – )(F 1 + T 1) F 2 = (. 2)(12) + (1 –. 2)(11 + 2) = 2. 4 + (. 8)(13) = 2. 4 + 10. 4 = 12. 8 units 4 - 80

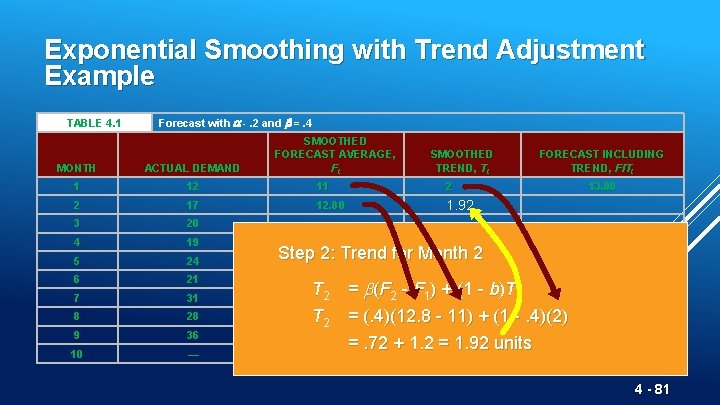
Exponential Smoothing with Trend Adjustment Example TABLE 4. 1 Forecast with -. 2 and b =. 4 SMOOTHED FORECAST AVERAGE, Ft SMOOTHED TREND, Tt MONTH ACTUAL DEMAND 1 12 11 2 2 17 12. 80 1. 92 3 20 4 19 5 24 6 21 7 31 8 28 9 36 10 — FORECAST INCLUDING TREND, FITt 13. 00 Step 2: Trend for Month 2 T 2 = (F 2 - F 1) + (1 - b)T 1 T 2 = (. 4)(12. 8 - 11) + (1 -. 4)(2) =. 72 + 1. 2 = 1. 92 units 4 - 81

Exponential Smoothing with Trend Adjustment Example TABLE 4. 1 Forecast with -. 2 and b =. 4 SMOOTHED FORECAST AVERAGE, Ft SMOOTHED TREND, Tt MONTH ACTUAL DEMAND 1 12 11 2 2 17 12. 80 1. 92 3 20 4 19 5 24 6 21 7 31 8 28 9 36 10 — FORECAST INCLUDING TREND, FITt 13. 00 14. 72 Step 3: Calculate FIT for Month 2 FIT 2 = F 2 + T 2 FIT 2 = 12. 8 + 1. 92 = 14. 72 units 4 - 82

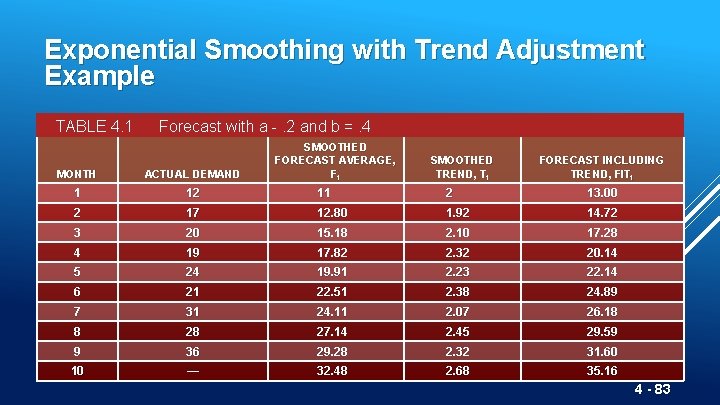
Exponential Smoothing with Trend Adjustment Example TABLE 4. 1 Forecast with a -. 2 and b =. 4 SMOOTHED FORECAST AVERAGE, Ft SMOOTHED TREND, Tt FORECAST INCLUDING TREND, FITt MONTH ACTUAL DEMAND 1 12 11 2 13. 00 2 17 12. 80 1. 92 14. 72 3 20 15. 18 2. 10 17. 28 4 19 17. 82 2. 32 20. 14 5 24 19. 91 2. 23 22. 14 6 21 22. 51 2. 38 24. 89 7 31 24. 11 2. 07 26. 18 8 28 27. 14 2. 45 29. 59 9 36 29. 28 2. 32 31. 60 10 — 32. 48 2. 68 35. 16 4 - 83

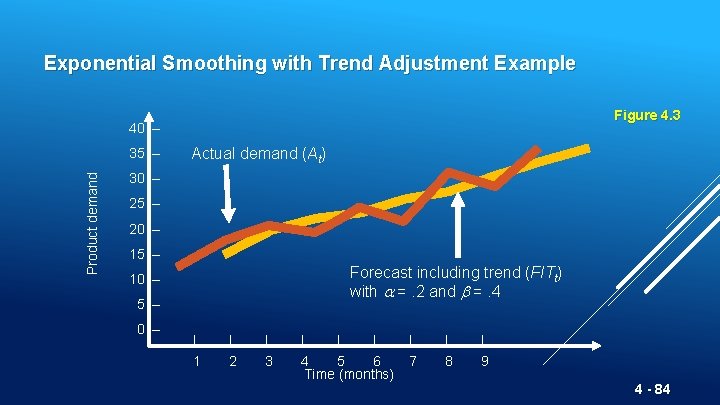
Exponential Smoothing with Trend Adjustment Example Figure 4. 3 40 – Product demand 35 – Actual demand (At) 30 – 25 – 20 – 15 – Forecast including trend (FITt) with =. 2 and =. 4 10 – 5 – 0 – | | | 1 2 3 4 5 6 Time (months) | | | 7 8 9 4 - 84

4. PROYEKSI TREN 4 - 85

Proyeksi tren Menyesuaikan garis tren ke titik-titik data historis untuk memproyeksikan jangka menengah dan jangka panjang Tren garis lurus dapat diperleh dengan teknik kuadrat terkecil y^ = a + bx di mana y^ = nilai yg dihitung dari variabel yang diprediksi (variabel terikat) a = intersep sumbu y b = kemiringan garis regresi x = variabel bebas (periode waktu) 4 - 86

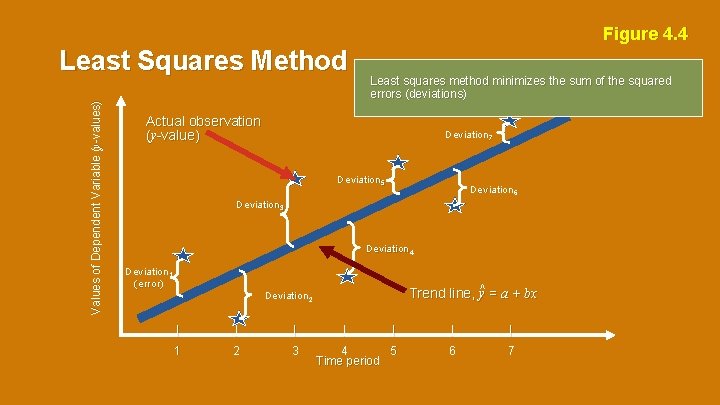
Figure 4. 4 Values of Dependent Variable (y-values) Least Squares Method Least squares method minimizes the sum of the squared errors (deviations) Actual observation (y-value) Deviation 7 Deviation 5 Deviation 6 Deviation 3 Deviation 4 Deviation 1 (error) Trend line, y^ = a + bx Deviation 2 | | | 1 2 3 | | 4 5 Time period 6 7 4 - 87

Least Squares Method Equations to calculate the regression variables 19 Maret 4 - 88

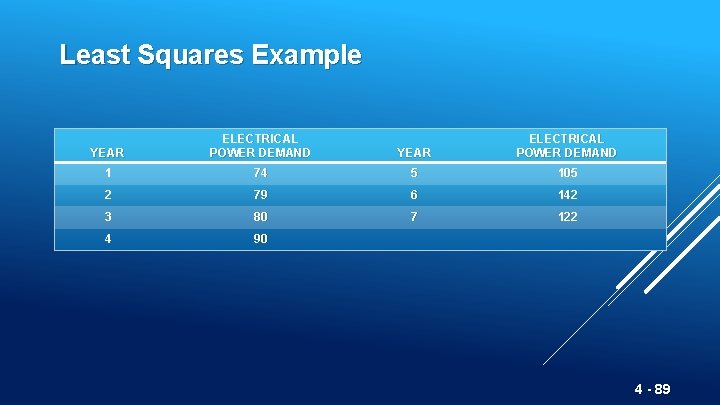
Least Squares Example YEAR ELECTRICAL POWER DEMAND 1 74 5 105 2 79 6 142 3 80 7 122 4 90 4 - 89

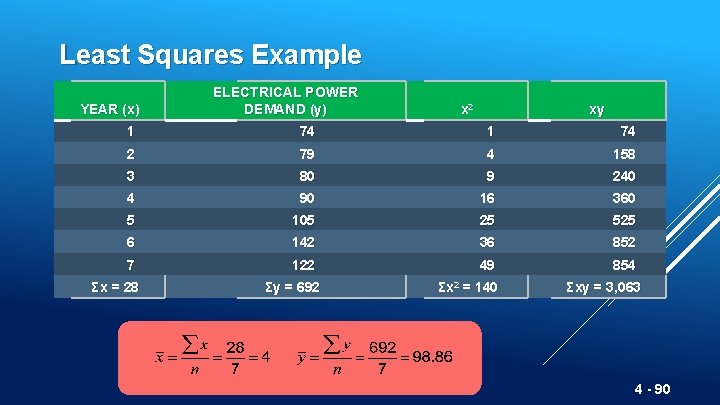
Least Squares Example YEAR (x) ELECTRICAL POWER DEMAND (y) x 2 xy 1 74 2 79 4 158 3 80 9 240 4 90 16 360 5 105 25 525 6 142 36 852 7 122 49 854 Σx = 28 Σy = 692 Σx 2 = 140 Σxy = 3, 063 4 - 90

Least Squares Example YEAR (x) ELECTRICAL POWER DEMAND (y) x 2 xy 1 74 2 79 4 158 3 80 9 240 4 90 16 360 5 105 25 525 6 142 36 852 7 122 49 854 Σx = 28 Σy = 692 Σx 2 = 140 Σxy = 3, 063 Demand in year 8 = 56. 70 + 10. 54(8) = 141. 02, or 141 megawatts 4 - 91

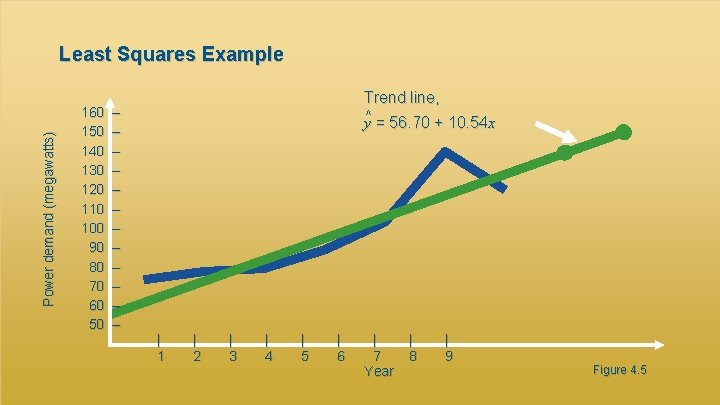
Power demand (megawatts) Least Squares Example 160 – 150 – 140 – 130 – 120 – 110 – 100 – 90 – 80 – 70 – 60 – 50 – Trend line, ^ y = 56. 70 + 10. 54 x | 1 | 2 | 3 | 4 | 5 | 6 | 7 Year | 8 | 9 Figure 4. 5 4 - 92

Least Squares Requirements 1. Kita selalu menempatkan data untuk memastikan hubungan linear 2. Kita tidak memprediksi periode waktu jauh melampaui database 3. Deviasi sekitar garis kuadrat terkecil diasumsikan acak 4 - 93

Seasonal Variations In Data Model musiman multiplikatif dapat menyesuaikan data tren untuk variasi musiman dalam permintaan 4 - 94

Seasonal Variations In Data Langkah-langkah dalam proses untuk musim bulanan : 1. Temukan permintaan historis rata-rata untuk setiap bulan 2. Hitung rata-rata permintaan selama semua bulan 3. Hitung indeks musiman untuk setiap bulan 4. Perkirakan total permintaan tahun depan 5. Bagilah perkiraan total permintaan ini dengan jumlah bulan, lalu kalikan dengan indeks musiman untuk bulan itu. Find average historical demand for each month 4 - 95

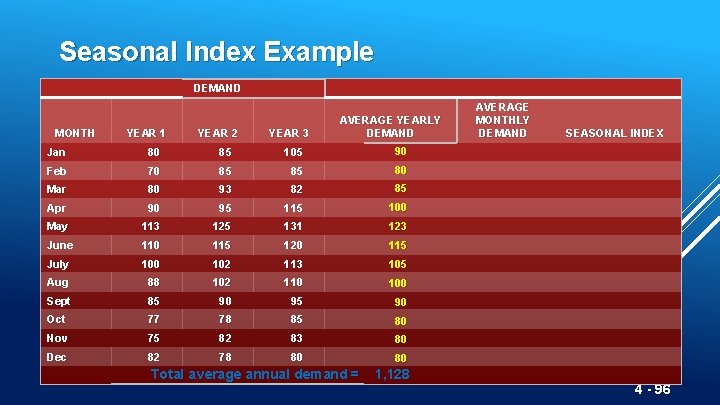
Seasonal Index Example DEMAND MONTH YEAR 1 YEAR 2 YEAR 3 AVERAGE YEARLY DEMAND Jan 80 85 105 90 Feb 70 85 85 80 Mar 80 93 82 85 Apr 90 95 115 100 May 113 125 131 123 June 110 115 120 115 July 100 102 113 105 Aug 88 102 110 100 Sept 85 90 95 90 Oct 77 78 85 80 Nov 75 82 83 80 Dec 82 78 80 80 Total average annual demand = 1, 128 AVERAGE MONTHLY DEMAND SEASONAL INDEX 4 - 96

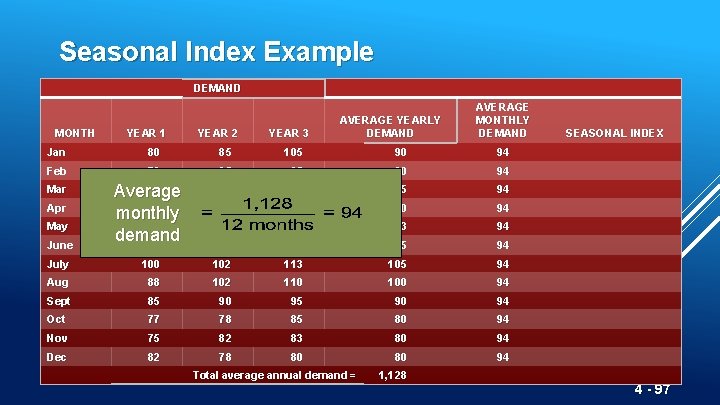
Seasonal Index Example DEMAND MONTH YEAR 1 YEAR 2 YEAR 3 AVERAGE YEARLY DEMAND AVERAGE MONTHLY DEMAND Jan 80 85 105 90 94 Feb 70 85 85 80 94 93 82 85 94 95 115 100 94 125 131 123 94 115 120 115 94 June 80 Average 90 monthly 113 demand 110 July 100 102 113 105 94 Aug 88 102 110 100 94 Sept 85 90 94 Oct 77 78 85 80 94 Nov 75 82 83 80 94 Dec 82 78 80 80 94 Mar Apr May Total average annual demand = 1, 128 SEASONAL INDEX 4 - 97

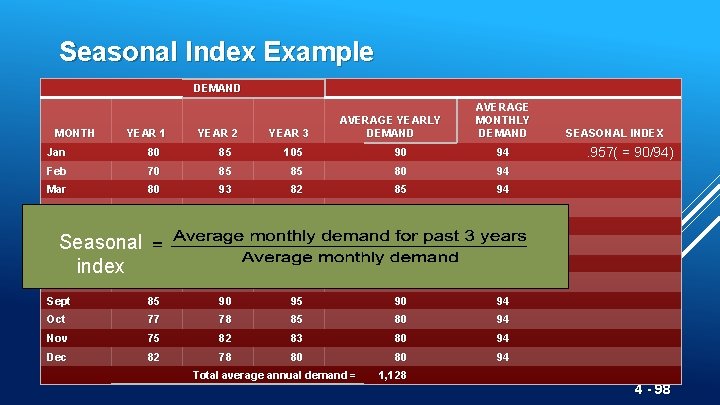
Seasonal Index Example DEMAND MONTH YEAR 1 YEAR 2 YEAR 3 AVERAGE YEARLY DEMAND AVERAGE MONTHLY DEMAND Jan 80 85 105 90 94 Feb 70 85 85 80 94 Mar 80 93 82 85 94 Apr 90 95 115 100 94 May 113 125 131 123 94 115 120 115 94 102 113 105 94 Seasonal 110 July index 100 June Aug 88 102 110 100 94 Sept 85 90 94 Oct 77 78 85 80 94 Nov 75 82 83 80 94 Dec 82 78 80 80 94 Total average annual demand = 1, 128 SEASONAL INDEX . 957( = 90/94) 4 - 98

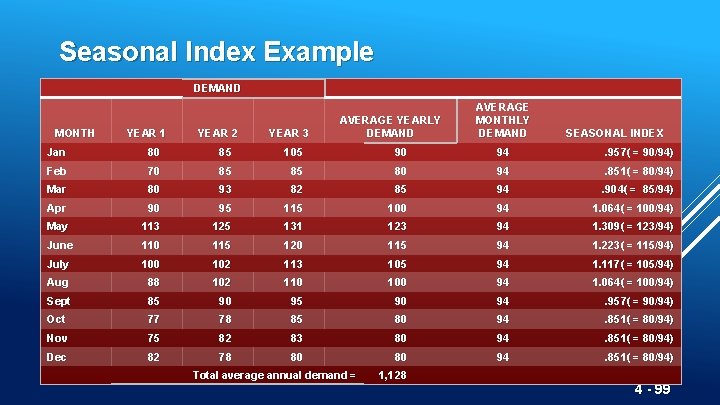
Seasonal Index Example DEMAND MONTH YEAR 1 YEAR 2 YEAR 3 AVERAGE YEARLY DEMAND AVERAGE MONTHLY DEMAND SEASONAL INDEX Jan 80 85 105 90 94 . 957( = 90/94) Feb 70 85 85 80 94 . 851( = 80/94) Mar 80 93 82 85 94 . 904( = 85/94) Apr 90 95 115 100 94 1. 064( = 100/94) May 113 125 131 123 94 1. 309( = 123/94) June 110 115 120 115 94 1. 223( = 115/94) July 100 102 113 105 94 1. 117( = 105/94) Aug 88 102 110 100 94 1. 064( = 100/94) Sept 85 90 94 . 957( = 90/94) Oct 77 78 85 80 94 . 851( = 80/94) Nov 75 82 83 80 94 . 851( = 80/94) Dec 82 78 80 80 94 . 851( = 80/94) Total average annual demand = 1, 128 4 - 99

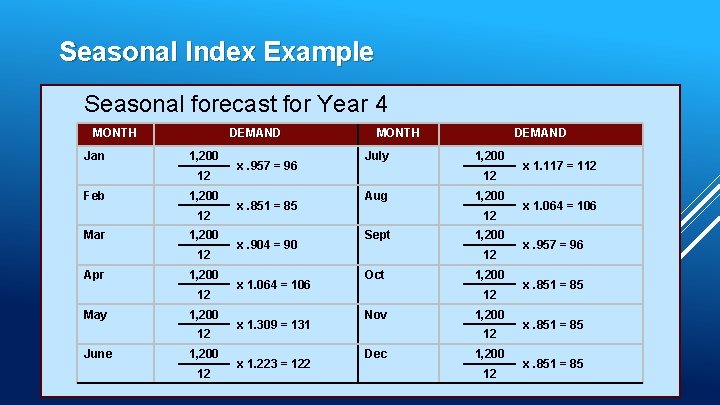
Seasonal Index Example Seasonal forecast for Year 4 MONTH Jan DEMAND 1, 200 12 Feb 1, 200 12 Mar 1, 200 12 Apr 1, 200 12 May 1, 200 12 June 1, 200 12 x. 957 = 96 x. 851 = 85 x. 904 = 90 x 1. 064 = 106 x 1. 309 = 131 x 1. 223 = 122 MONTH July DEMAND 1, 200 12 Aug 1, 200 12 Sept 1, 200 12 Oct 1, 200 12 Nov 1, 200 12 Dec 1, 200 12 x 1. 117 = 112 x 1. 064 = 106 x. 957 = 96 x. 851 = 85 4 - 100

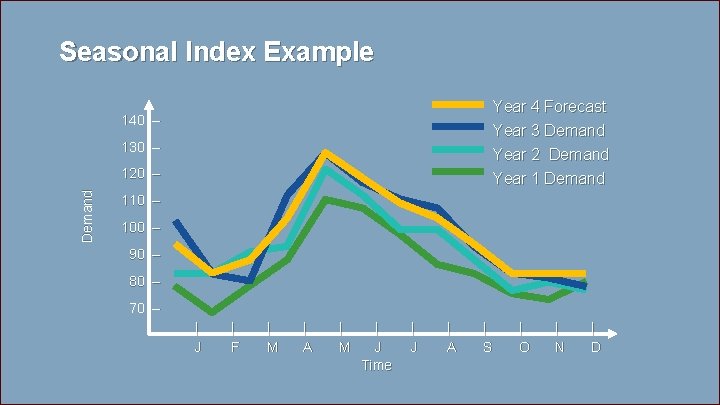
Seasonal Index Example Year 4 Forecast Year 3 Demand 140 – 130 – Year 2 Demand Year 1 Demand 120 – 110 – 100 – 90 – 80 – 70 – | J | F | M | A | M | J Time | J | A | S | O | N | D 4 - 101

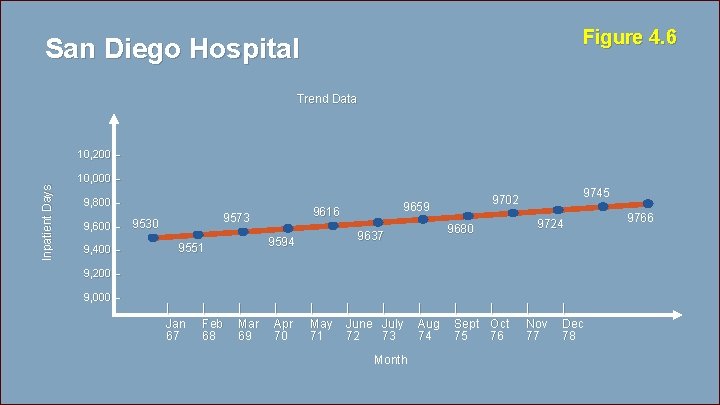
Figure 4. 6 San Diego Hospital Trend Data Inpatient Days 10, 200 – 10, 000 – 9, 800 – 9, 400 – 9616 9573 9, 600 – 9530 9724 9680 9637 9594 9551 9745 9702 9659 9766 9, 200 – 9, 000 – | Jan 67 | Feb 68 | Mar 69 | Apr 70 | May 71 | June 72 | July 73 | Aug 74 | Sept 75 | Oct 76 | Nov 77 | Dec 78 Month © 2014 Pearson Education, Inc. 4 - 102

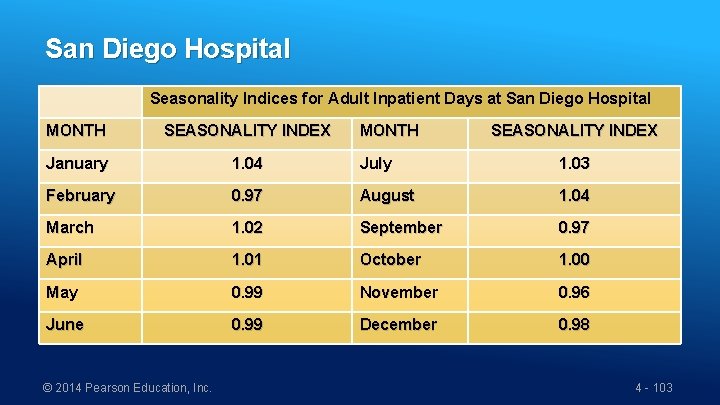
San Diego Hospital Seasonality Indices for Adult Inpatient Days at San Diego Hospital MONTH SEASONALITY INDEX January 1. 04 July 1. 03 February 0. 97 August 1. 04 March 1. 02 September 0. 97 April 1. 01 October 1. 00 May 0. 99 November 0. 96 June 0. 99 December 0. 98 © 2014 Pearson Education, Inc. MONTH SEASONALITY INDEX 4 - 103

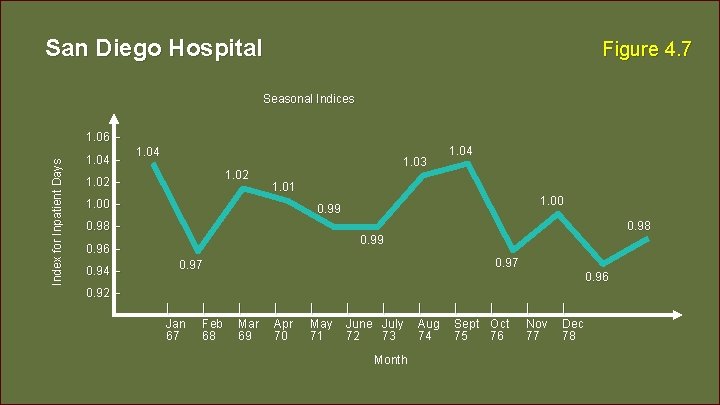
San Diego Hospital Figure 4. 7 Seasonal Indices Index for Inpatient Days 1. 06 – 1. 04 1. 02 – 1. 03 1. 01 1. 00 – 1. 00 0. 99 0. 98 – 0. 98 0. 99 0. 96 – 0. 94 – 1. 04 0. 97 0. 96 0. 92 – | Jan 67 | Feb 68 | Mar 69 | Apr 70 | May 71 | June 72 | July 73 | Aug 74 | Sept 75 | Oct 76 | Nov 77 | Dec 78 Month © 2014 Pearson Education, Inc. 4 - 104

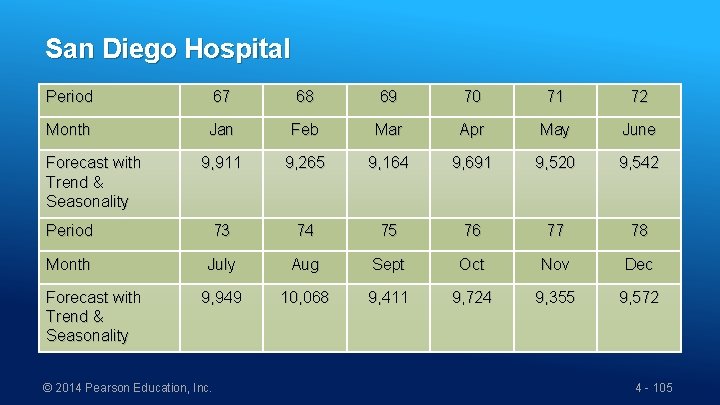
San Diego Hospital Period 67 68 69 70 71 72 Month Jan Feb Mar Apr May June 9, 911 9, 265 9, 164 9, 691 9, 520 9, 542 Period 73 74 75 76 77 78 Month July Aug Sept Oct Nov Dec 9, 949 10, 068 9, 411 9, 724 9, 355 9, 572 Forecast with Trend & Seasonality © 2014 Pearson Education, Inc. 4 - 105

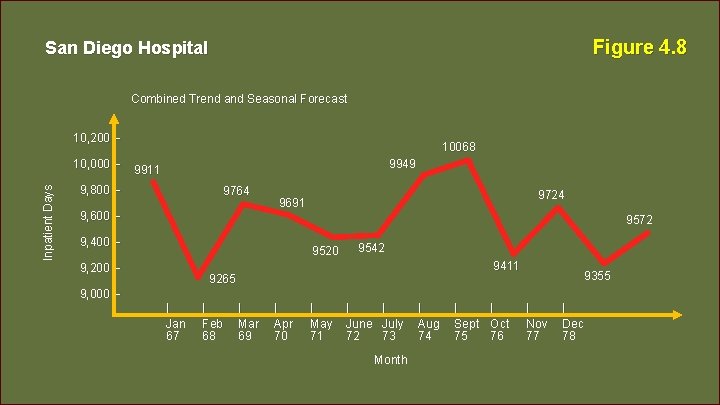
Figure 4. 8 San Diego Hospital Combined Trend and Seasonal Forecast 10, 200 – Inpatient Days 10, 000 – 10068 9949 9911 9, 800 – 9764 9, 600 – 9724 9691 9572 9, 400 – 9520 9, 200 – 9542 9411 9265 9355 9, 000 – | Jan 67 | Feb 68 | Mar 69 | Apr 70 | May 71 | June 72 | July 73 | Aug 74 | Sept 75 | Oct 76 | Nov 77 | Dec 78 Month © 2014 Pearson Education, Inc. 4 - 106

Adjusting Trend Data Quarter I: Quarter III: Quarter IV: © 2014 Pearson Education, Inc. 4 - 107

MODEL ASOSIATIF 4 - 108

Associative Forecasting Digunakan ketika perubahan dalam satu atau lebih variabel independen dapat digunakan untuk memprediksi perubahan dalam variabel dependen Teknik yang paling umum adalah analisis regresi linier Kita menerapkan teknik ini seperti yang kita lakukan dalam contoh time-series 4 - 109

Peramalan asosiatif Hasil peramalan didasarkan pada variabel prediktor menggunakan teknik kuadrat terkecil ^ y = a + bx ^ di mana y = nilai variabel terikat (yang diramalkan) a = intersep sumbu y b = kemiringan garis regresi x = variabel bebas (prediktor) 4 - 110

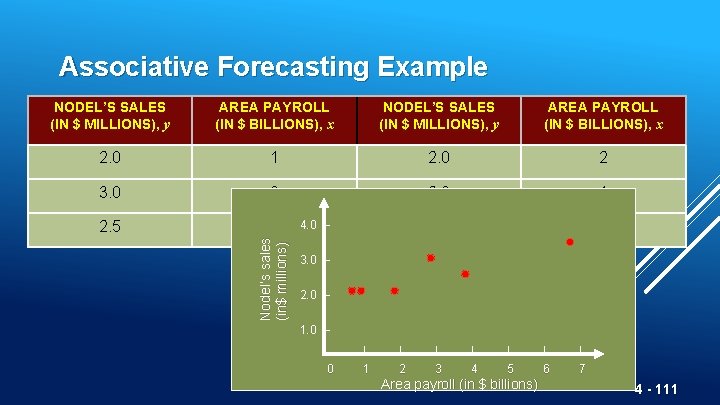
Associative Forecasting Example AREA PAYROLL (IN $ BILLIONS), x NODEL’S SALES (IN $ MILLIONS), y AREA PAYROLL (IN $ BILLIONS), x 2. 0 1 2. 0 2 3. 0 3 2. 0 1 2. 5 4 3. 5 7 Nodel’s sales (in$ millions) NODEL’S SALES (IN $ MILLIONS), y 4. 0 – 3. 0 – 2. 0 – 1. 0 – 0 | | | | 1 2 3 4 5 6 7 Area payroll (in $ billions) 4 - 111

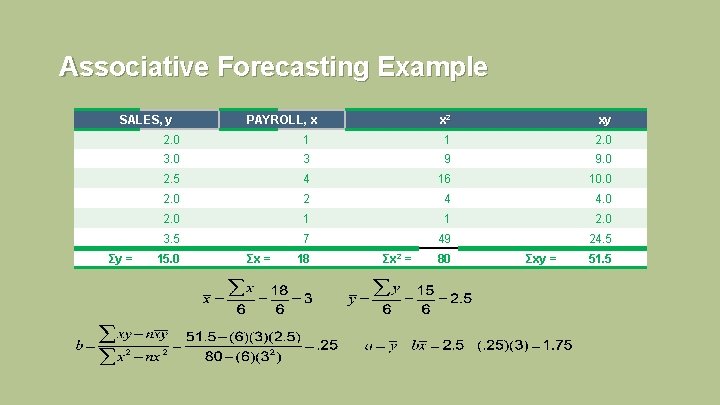
Associative Forecasting Example SALES, y Σy = PAYROLL, x x 2 xy 2. 0 1 1 2. 0 3 9 9. 0 2. 5 4 16 10. 0 2 4 4. 0 2. 0 1 1 2. 0 3. 5 7 49 24. 5 15. 0 Σx = 18 Σx 2 = 80 Σxy = 51. 5 4 - 112

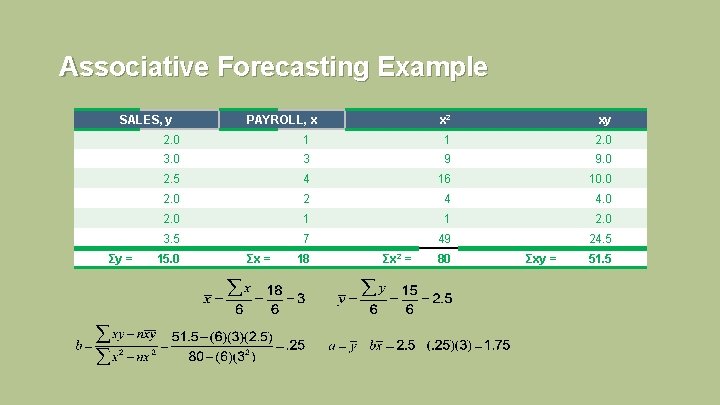
Associative Forecasting Example SALES, y Σy = PAYROLL, x x 2 xy 2. 0 1 1 2. 0 3 9 9. 0 2. 5 4 16 10. 0 2 4 4. 0 2. 0 1 1 2. 0 3. 5 7 49 24. 5 15. 0 Σx = 18 Σx 2 = 80 Σxy = 51. 5 4 - 113

Associative Forecasting Example SALES, y Σy = PAYROLL, x x 2 xy 2. 0 1 1 2. 0 3 9 9. 0 2. 5 4 16 10. 0 2 4 4. 0 2. 0 1 1 2. 0 3. 5 7 49 24. 5 15. 0 Σx = 18 Σx 2 = 80 Σxy = 51. 5 4 - 114

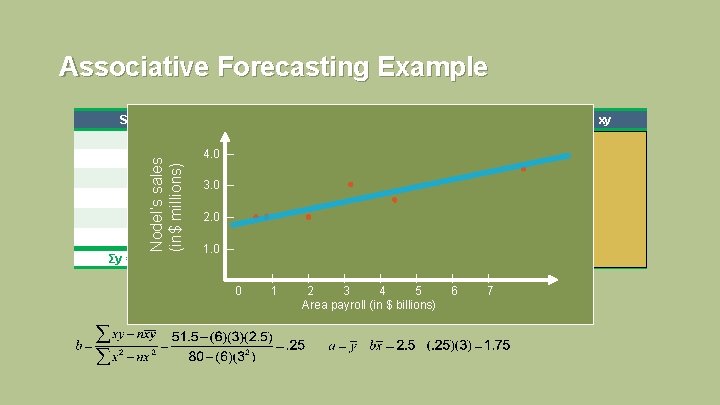
Associative Forecasting Example SALES, y PAYROLL, x 2. 0 xy 1 1 2. 0 4. 0 – 3 9 9. 0 2. 5 3. 0 – 4 16 10. 0 2 4 4. 0 1 1 2. 0 7 49 24. 5 Nodel’s sales (in$ millions) 3. 0 2. 0 3. 5 Σy = x 2 15. 0 2. 0 – 1. 0 – Σx = 18 | 0 1 | Σx 2 = | | 80 | 2 3 4 5 Area payroll (in $ billions) Σxy = | | 6 7 51. 5 4 - 115

Associative Forecasting Example If payroll next year is estimated to be $6 billion, then: Sales (in $ millions) = 1. 75 +. 25(6) = 1. 75 + 1. 5 = 3. 25 Sales = $3, 250, 000 4 - 116

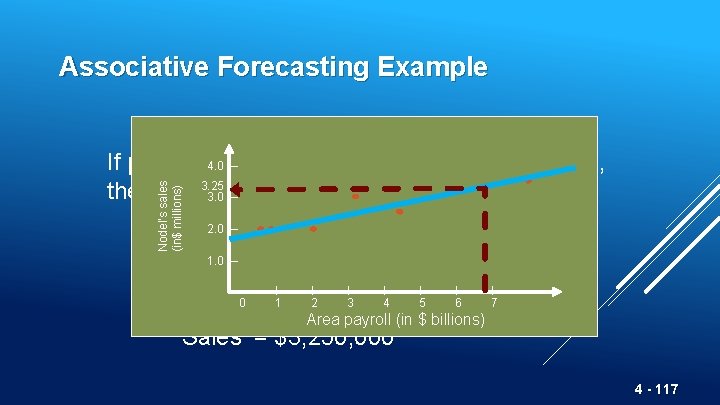
Associative Forecasting Example Nodel’s sales (in$ millions) 4. 0 – If payroll next year is estimated to be $6 billion, 3. 25 then: 3. 0 – 2. 0 – Sales (in$ millions) = 1. 75 +. 25(6) 1. 0 – = 1. 75 + 1. 5 = 3. 25 | | | | 0 1 2 3 4 5 6 7 Area payroll (in $ billions) Sales = $3, 250, 000 4 - 117

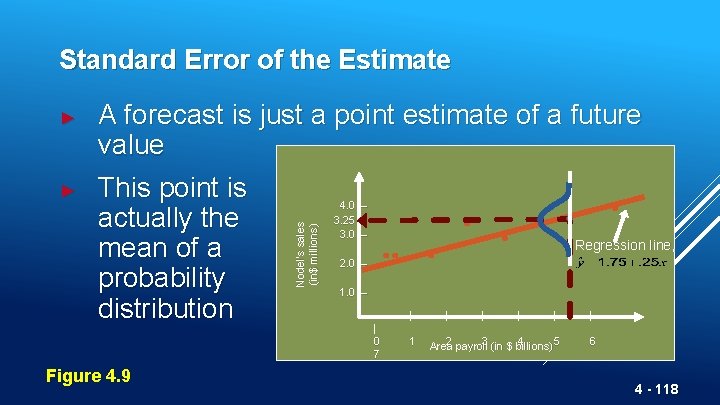
Standard Error of the Estimate ► Nodel’s sales (in$ millions) ► A forecast is just a point estimate of a future value This point is actually the Regression line, mean of a probability distribution 4. 0 – 3. 25 3. 0 – 2. 0 – 1. 0 – | | 0 7 Figure 4. 9 1 | | | 2 3 4 5 Area payroll (in $ billions) 6 4 - 118

Standard Error of the Estimate where y = y-value of each data point yc = computed value of the dependent variable, from the regression equation n = number of data points 4 - 119

Standard Error of the Estimate Computationally, this equation is considerably easier to use We use the standard error to set up prediction intervals around the point estimate 4 - 120

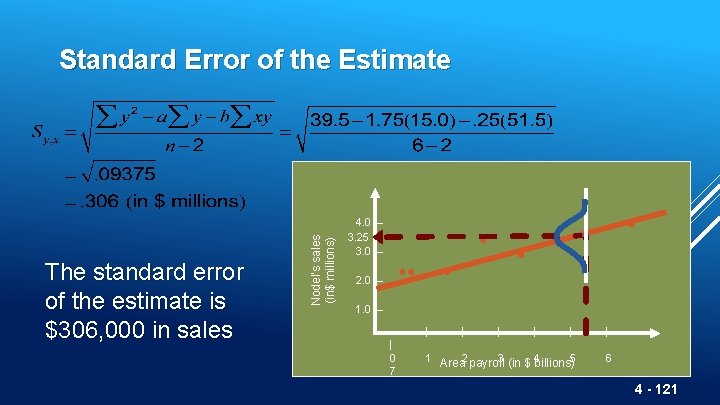
The standard error of the estimate is $306, 000 in sales Nodel’s sales (in$ millions) Standard Error of the Estimate 4. 0 – 3. 25 3. 0 – 2. 0 – 1. 0 – | | 0 7 1 | | | 2 3 4 5 Area payroll (in $ billions) 6 4 - 121

Correlation ► How strong is the linear relationship between the variables? ► Correlation does not necessarily imply causality! ► Coefficient of correlation, r, measures degree of association ► Values range from -1 to +1 4 - 122

Correlation Coefficient 4 - 123

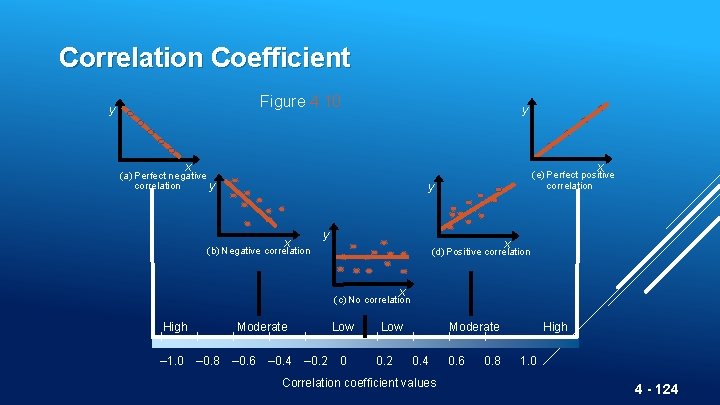
Correlation Coefficient Figure 4. 10 y y x x (a) Perfect negative correlation y (e) Perfect positive correlation y y x x (b) Negative correlation (d) Positive correlation x (c) No correlation High Moderate | | | – 1. 0 – 0. 8 – 0. 6 | | – 0. 4 – 0. 2 Low 0 | Low 0. 2 Moderate | | | 0. 4 0. 6 0. 8 Correlation coefficient values High 1. 0 4 - 124

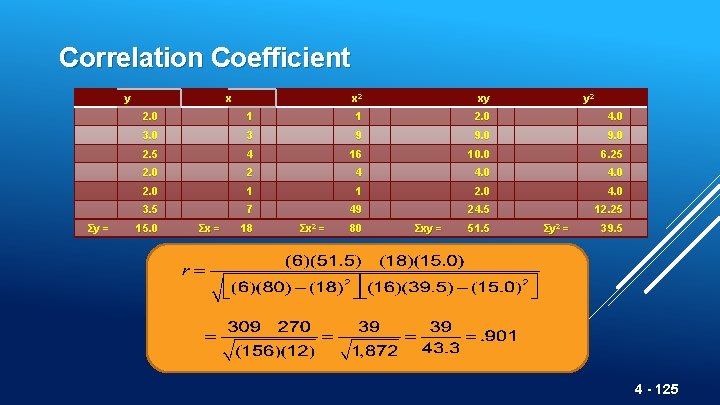
Correlation Coefficient y Σy = x x 2 xy y 2 2. 0 1 1 2. 0 4. 0 3 9 9. 0 2. 5 4 16 10. 0 6. 25 2. 0 2 4 4. 0 2. 0 1 1 2. 0 4. 0 3. 5 7 49 24. 5 12. 25 15. 0 Σx = 18 Σx 2 = 80 Σxy = 51. 5 Σy 2 = 39. 5 4 - 125

Correlation o Coefficient of Determination, r 2, measures the percent of change in y predicted by the change in x o Values range from 0 to 1 o Easy to interpret For the Nodel Construction example: r =. 901 r 2 =. 81 4 - 126

Multiple-Regression Analysis Jika lebih dari satu variabel independen akan digunakan dalam model, regresi linier dapat diperluas ke regresi ganda untuk mengakomodasi beberapa variabel independen Secara komputasi, ini cukup kompleks dan umumnya dilakukan di komputer 4 - 127

Multiple-Regression Analysis Dalam contoh Nodel, termasuk suku bunga dalam model memberikan persamaan baru: Koefisien korelasi meningkat sebesar r =. 96 menunjukkan model ini melakukan pekerjaan yang lebih baik dalam memprediksi perubahan dalam penjualan konstruksi Sales = 1. 80 +. 30(6) - 5. 0(. 12) = 3. 00 Sales = $3, 000 4 - 128

Monitoring and Controlling Forecasts Tracking Signal ► ► Mengukur seberapa baik ramalan memprediksi nilai yang sebenarnya Ratio of cumulative forecast errors to mean absolute deviation (MAD) ► ► Sinyal pelacakan yang baik memiliki nilai yang rendah Jika perkiraan terus-menerus tinggi atau rendah, ramalan memiliki kesalahan bias 4 - 129

Monitoring and Controlling Forecasts Tracking = signal Cumulative error MAD 4 - 130

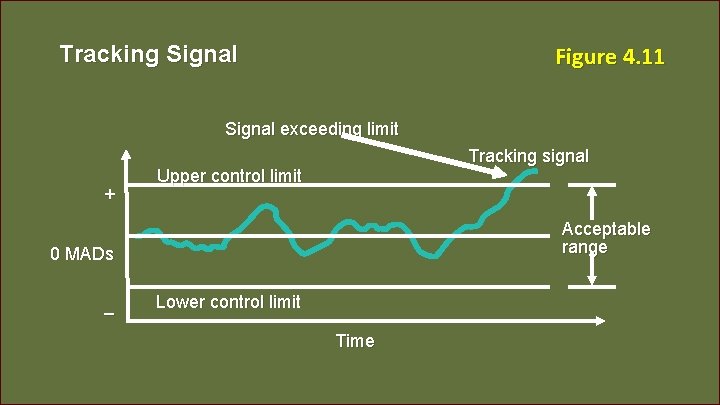
Tracking Signal Figure 4. 11 Signal exceeding limit + Tracking signal Upper control limit Acceptable range 0 MADs – Lower control limit Time 4 - 131

Tracking Signal Example ERROR CUM ERROR ABSOLUTE FORECAST ERROR CUM ABS FORECAST ERROR MAD TRACKING SIGNAL (CUM ERROR/MAD) 100 – 10 10. 0 – 10/10 = – 1 95 100 – 5 – 15 5 15 7. 5 – 15/7. 5 = – 2 3 115 100 +15 0 15 30 10. 0/10 = 0 4 100 110 – 10 10 40 10. 10/10 = – 1 5 125 110 +15 +5 15 55 11. 0 +5/11 = +0. 5 6 140 110 +35 30 85 14. 2 +35/14. 2 = +2. 5 QTR ACTUAL DEMAND FORECAST DEMAND 1 90 2 At the end of quarter 6, 4 - 132

Adaptive Smoothing o o Anda dapat menggunakan komputer untuk terus memantau kesalahan perkiraan dan menyesuaikan nilai koefisien a dan b yang digunakan dalam pemulusan eksponensial untuk terus meminimalkan kesalahan perkiraan Teknik ini disebut smoothing adaptif 4 - 133

Focus Forecasting q Dikembangkan di American Hardware Supply, berdasarkan dua prinsip: 1. Model peramalan yang canggih tidak selalu lebih baik daripada model sederhana q q 2. Tidak ada teknik tunggal yang harus digunakan untuk semua produk atau layanan Menggunakan data historis untuk menguji beberapa model perkiraan untuk masing-masing item Model peramalan dengan kesalahan terendah digunakan untuk meramalkan permintaan berikutnya 4 - 134

Forecasting in the Service Sector o Menyajikan tantangan yang tidak biasa o Kebutuhan khusus untuk catatan jangka pendek o Kebutuhan sangat berbeda sebagai fungsi industri dan produk o Liburan dan acara kalender lainnya o Peristiwa yang tidak biasa 4 - 135

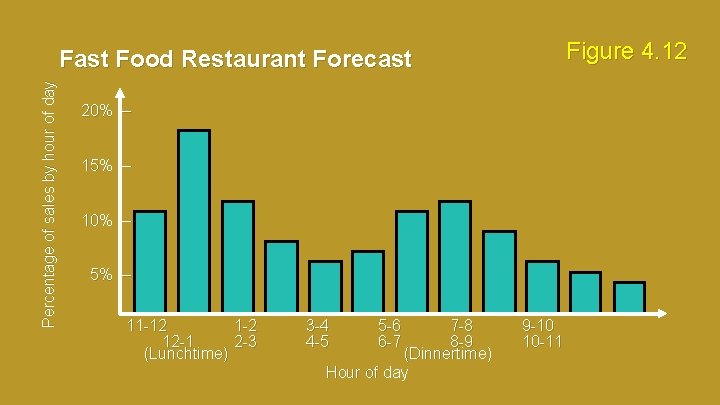
Figure 4. 12 Percentage of sales by hour of day Fast Food Restaurant Forecast 20% – 15% – 10% – 5% – 11 -12 1 -2 12 -1 2 -3 (Lunchtime) 3 -4 4 -5 5 -6 6 -7 7 -8 8 -9 (Dinnertime) Hour of day 9 -10 10 -11 4 - 136

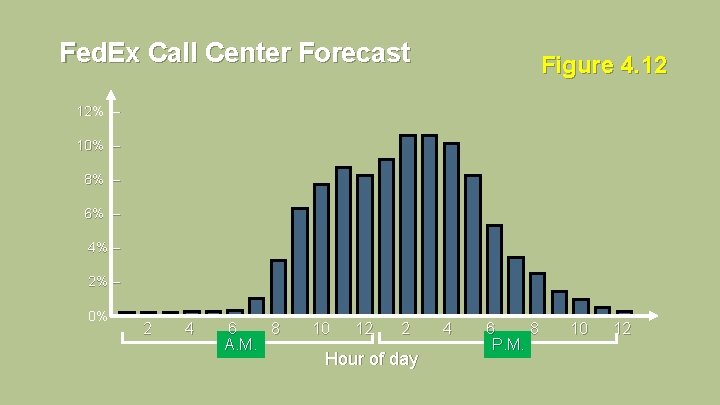
Fed. Ex Call Center Forecast Figure 4. 12 12% – 10% – 8% – 6% – 4% – 2% – 0% – 2 4 6 8 A. M. 10 12 2 Hour of day 4 6 8 P. M. 10 12 4 - 137