B Trees Disk based tree index Creative Commons

B Trees Disk based tree index Creative Commons License – Curt Hill

Introduction • A BTree is a multiway, tree that usually resides on disk – Most CS tree are binary and in memory • The basis of many ISAM or VSAM implementations as well as DB clustered and unclustered indices • B is for Bayer the person who worked out the original scheme Creative Commons License – Curt Hill

Characteristics: • Always balanced • Leaves are at same level • Do not waste space, all nodes are at least half full • Insertion and deletion do not cause the rewriting of the large parts of tree • Concurrency is well supported with minimal locking of pages Creative Commons License – Curt Hill

Variations • The standard BTree will be discussed first – Seldom actually used • The B+Tree and the B*Tree are the common variants – The modifications for these will also be discussed Creative Commons License – Curt Hill

Terminology • The three terms that need to be understood are pointers, records and pages • Pointer is a page identifier – The address of a page in any form – Usually compact • The record is the item to be stored – Always includes key and data – Key may have any form • The page is the block or page of the file system – Must be larger than the record Creative Commons License – Curt Hill

BTree Node • BTrees are a set of nodes of three types • The root node is the beginning of the tree – The entire tree is the descendents of the root • A leaf node has no descendents • Interior nodes have both ancestors and descendents Creative Commons License – Curt Hill

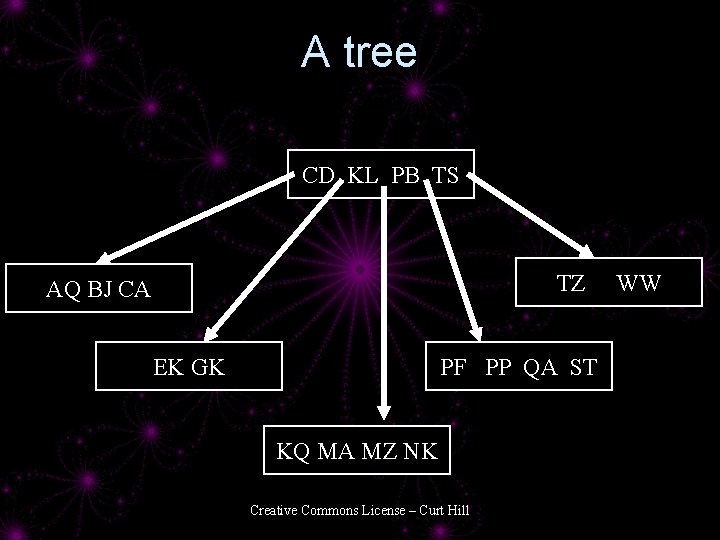
A tree CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

Nodes • Always one more pointer than record • Always has between N and 2 N records – Except root • N is chosen based upon – Page size – How many records and pointer fit • The previous tree is a 4 -5 tree – 4 records – 5 pointers – N=2 Creative Commons License – Curt Hill

Examples and Reality • This presentation will show trees with small Ns: 1 or 2 – These diagram nicely in Power. Point • Real trees have large Ns 50 – 100 • The N determines fan-out – High fan-out is good – If fan out is 2 then 50% of tree is eliminated from a search at each level – If fan out is 100 then 99% of tree is eliminated from a search at each level – High fan out makes a flat tree Creative Commons License – Curt Hill

Example numbers • Suppose that a BTree has average fanout of 50 • Suppose that BTree has 1 million entries • 1 disk access gets root • 3 disk accesses later obtains the leaf • A sequential search requires an average of 10000 disk accesses Creative Commons License – Curt Hill

Searching a BTree 1. 2. 3. 4. 5. 6. Start at root Is this key in this node? Yes – stop you are done No - Is this a leaf? Yes – this key does not exist - Stop No – find the pointer that is between the two surrounding values 7. Fetch this node – Go to step 2. Creative Commons License – Curt Hill

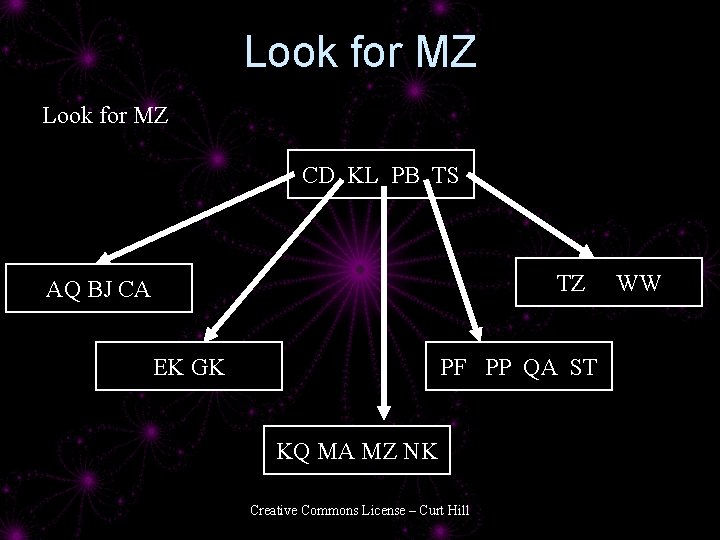
Look for MZ CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

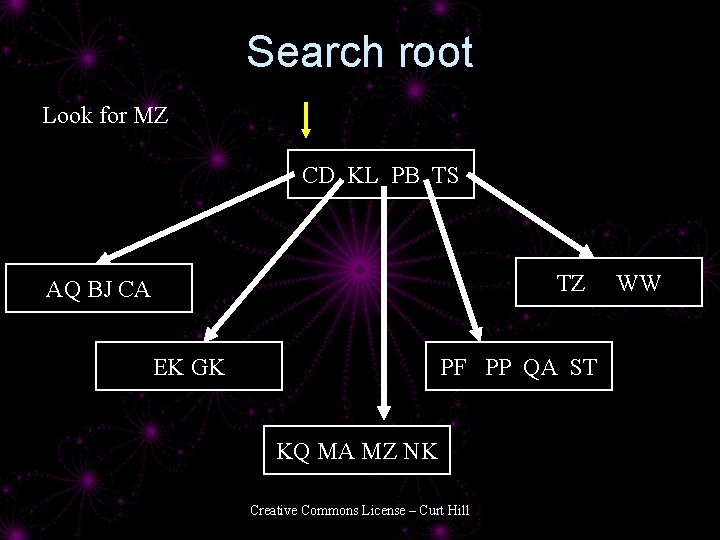
Search root Look for MZ CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

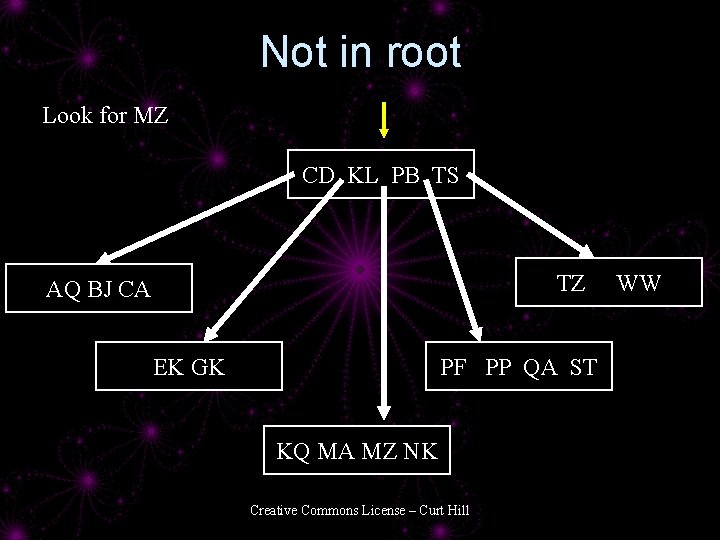
Not in root Look for MZ CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

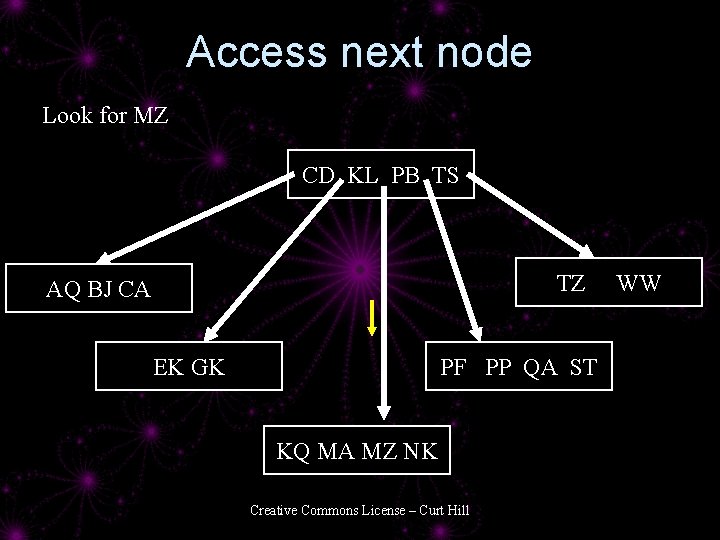
Access next node Look for MZ CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

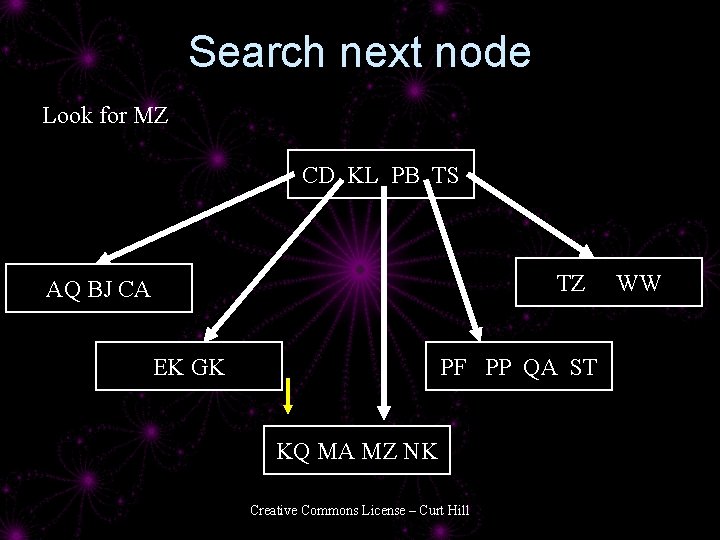
Search next node Look for MZ CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

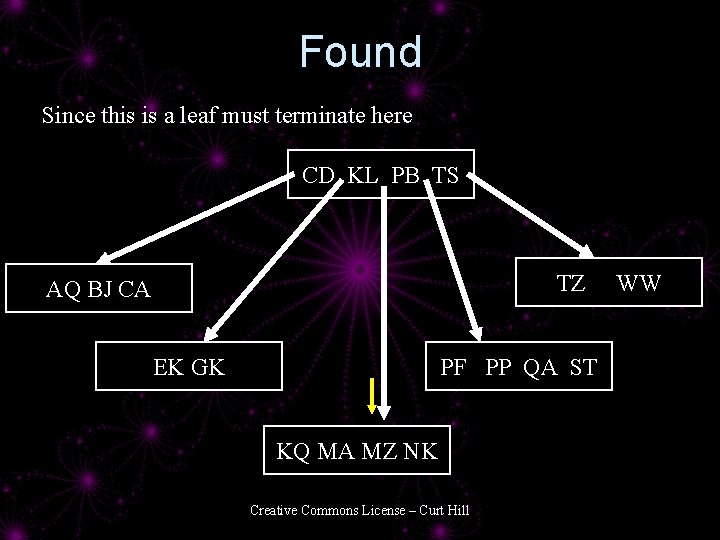
Found Since this is a leaf must terminate here CD KL PB TS TZ AQ BJ CA EK GK PF PP QA ST KQ MA MZ NK Creative Commons License – Curt Hill WW

Insertion and Deletion • The means by which new data is inserted and old is deleted is crucial to maintaining a BTree • These techniques were developed Bayer and their effectiveness caused this form of tree to catch on • The tree is never reorganized – This was a disadvantage of older ISAMs – Insertion and deletion do all the work Creative Commons License – Curt Hill

Insertion 1. Find the leaf that should contain the inserted value 2. Insert the record 3. Does the node have 2 N or fewer records? 4. Yes – Stop 5. No - Split the node 1. Make two nodes of N records 1. First N records and last N records 2. Promote the middle item into the ancestor 3. Go back to 2 Creative Commons License – Curt Hill

Example Insertion • Suppose a 2 -3 tree –N=1 – Key is a simple integer • Consider the following insertions: – 20, 40, 30, 15, 35, 7, 26, 18 Creative Commons License – Curt Hill

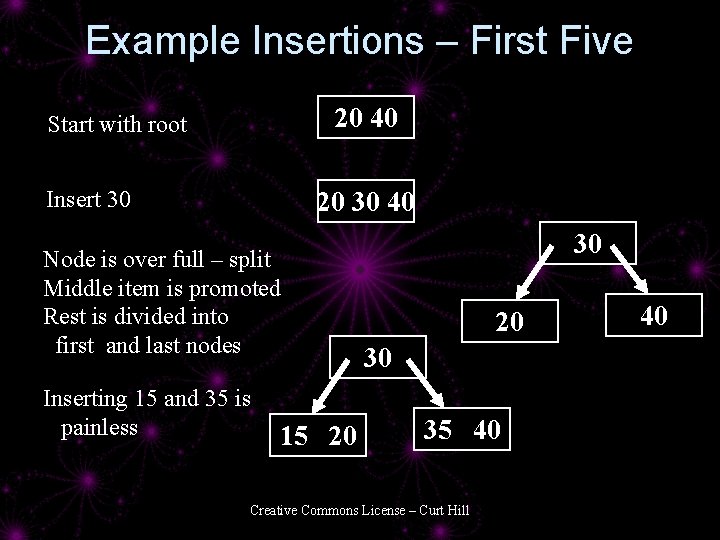
Example Insertions – First Five 20 40 Start with root Insert 30 20 30 40 Node is over full – split Middle item is promoted Rest is divided into first and last nodes Inserting 15 and 35 is painless 15 20 30 35 40 Creative Commons License – Curt Hill 40

Insertion Comments • Only the path between the root and the node containing the inserted node may be modified • This did not appear as significant in the example as it actually is when N is large • Usually most of tree is undisturbed • The root of the BTree that is currently being accessed is usually in memory Creative Commons License – Curt Hill

Deletion 1. 2. 3. 4. 5. Find the leaf that contains the value Delete the record Does the node have N or more records? Yes – Stop No – Merge the nodes 1. 2. 3. 4. Remove an item from the ancestor Pull into record that is short This may reduce the level Go back to 2 to delete the ancestor Creative Commons License – Curt Hill

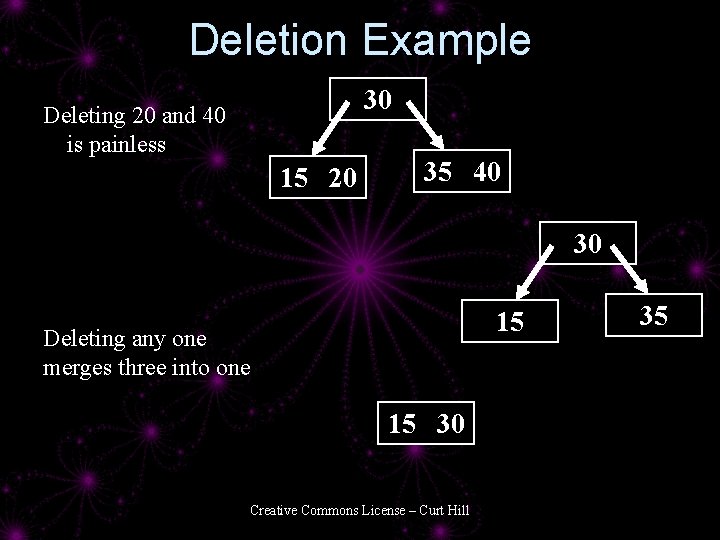
Deletion Example 30 Deleting 20 and 40 is painless 15 20 35 40 30 15 Deleting any one merges three into one 15 30 Creative Commons License – Curt Hill 35

Splitting/Merging • Relatively expensive – Wish to avoid if we can • Before splitting / merging – Look for a neighbor to carry or borrow an item – Do not split unless both neighbors are full – Do not merge unless both neighbors are at minimum Creative Commons License – Curt Hill

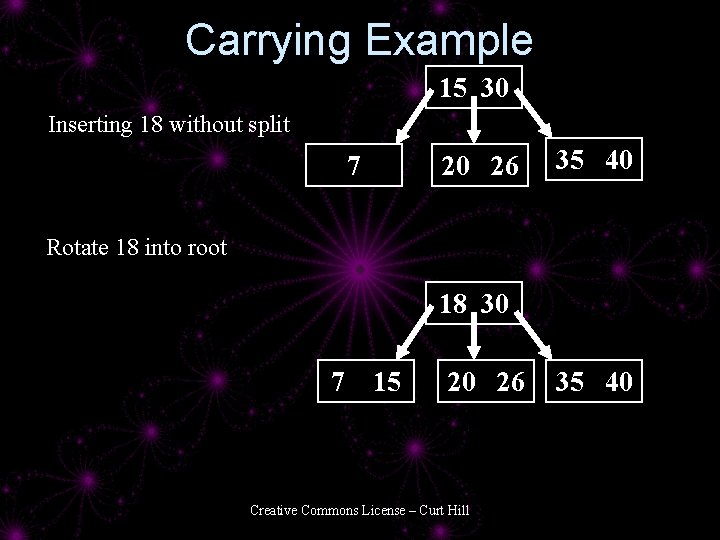
Carrying Example 15 30 Inserting 18 without split 7 20 26 35 40 Rotate 18 into root 18 30 7 15 20 26 Creative Commons License – Curt Hill 35 40

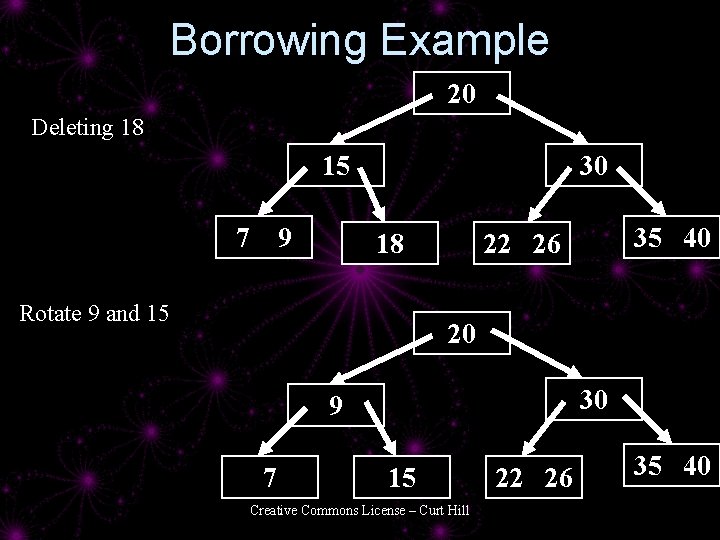
Borrowing Example 20 Deleting 18 15 7 9 30 18 Rotate 9 and 15 35 40 22 26 20 30 9 7 15 Creative Commons License – Curt Hill 22 26 35 40

Utilization • Each node of a BTree except root is between ½ full and full – Expected utilization is the ¾ full when the space occupied by root is negligible • Carrying records to adjacent nodes tends to increase this • Borrowing tends to decrease • Stable trees may also be compacted – Look for adjacent nodes that could be merged Creative Commons License – Curt Hill

BTree Variants: B*Tree • B*Tree – A BTree with only keys in the interior and root nodes – Data is all in leaves – Since the key is generally much smaller than the data this greatly increases fan-out – Two different kinds of pages • Leaves and root/interior nodes Creative Commons License – Curt Hill

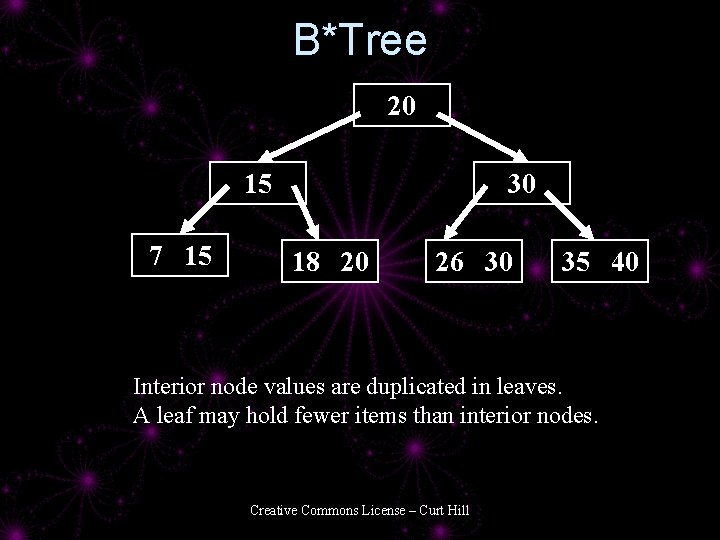
B*Tree 20 15 7 15 30 18 20 26 30 35 40 Interior node values are duplicated in leaves. A leaf may hold fewer items than interior nodes. Creative Commons License – Curt Hill

BTree Variants: B+Tree • A B*Tree – Keys only in ancestral nodes – Data only in leaves • Connect the leaves into a linked list • Foundation of most ISAMs • Follow the leaves for sequential access – Not slower than normal heap file • Search key for random access Creative Commons License – Curt Hill

Fanout of B+Tree • Suppose that: – – Key is 10 bytes Data is 79 bytes Pointer is 4 bytes Page size is 512 • N = 3 is largest node for a BTree – 3 -6 items per node • N = 62 is the largest node for a B*Tree – 62 -124 items per interior/root node – N = 3 for leaf nodes Creative Commons License – Curt Hill

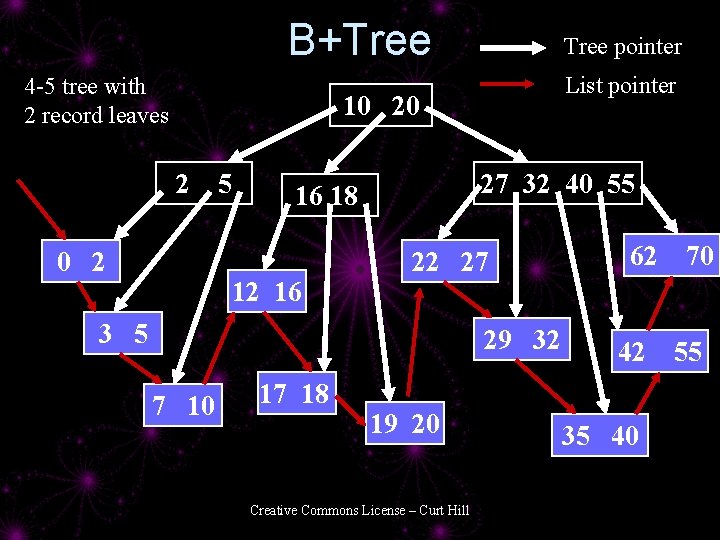
B+Tree 4 -5 tree with 2 record leaves Tree pointer List pointer 10 20 2 5 27 32 40 55 16 18 12 16 22 27 3 5 29 32 7 10 17 18 19 20 Creative Commons License – Curt Hill 62 42 35 40 70 55

Key Lengths • Many keys are relatively long – An integer is typically 4 bytes – Character string keys may be much longer • Names • Product codes – These are very sparse keys – They also take up too much space in the tree Creative Commons License – Curt Hill

Key Compression • The whole key is not always needed in the tree • Abbreviate the key to shorten it • Lose the ability to determine if the key is present without going to the leaves • Gain greater fan-out and flatter tree Creative Commons License – Curt Hill

Key Compression Savings • The fan-out may be increased by reducing the size of the key • Suppose a 19 character key and page id of 4 bytes in a 512 byte page • This makes for N = 11 – A 22 -23 tree • Reduce the key to 4 bytes – N = 32, a 64 -65 tree Creative Commons License – Curt Hill

Creating a B+Tree • Two ways: – Insert as has been shown – Bulk load • The normal insertion scheme works well for regular insertions • Bulk load works best for large number of insertions to create a new B+Tree Creative Commons License – Curt Hill

Bulk Load • Sort the data • Create the leaves in order and build the index over them • The index does a normal split mechanism Creative Commons License – Curt Hill

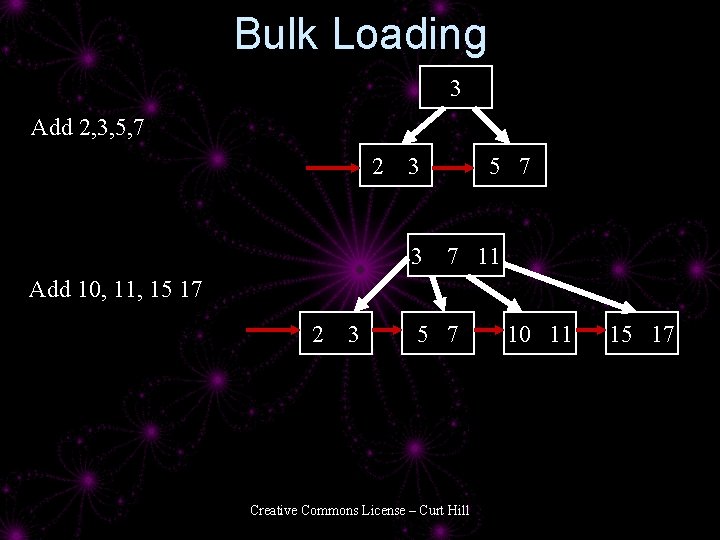
Bulk Loading 3 Add 2, 3, 5, 7 2 3 3 5 7 7 11 Add 10, 11, 15 17 2 3 5 7 Creative Commons License – Curt Hill 10 11 15 17

Clustered • All the examples so far are clustered • The lowest interior node has only one pointer to a block – Between two keys is a page of several entries – One key addresses many data items • B+Trees may also handle an unclustered index Creative Commons License – Curt Hill

Unclustered BTree Index • Essentially the same as a regular B+Tree with several exceptions • Uses another trees leaves • No data at all • In last interior level each key points at a separate leaf page • The leaves are in a completely different order than the interior nodes Creative Commons License – Curt Hill

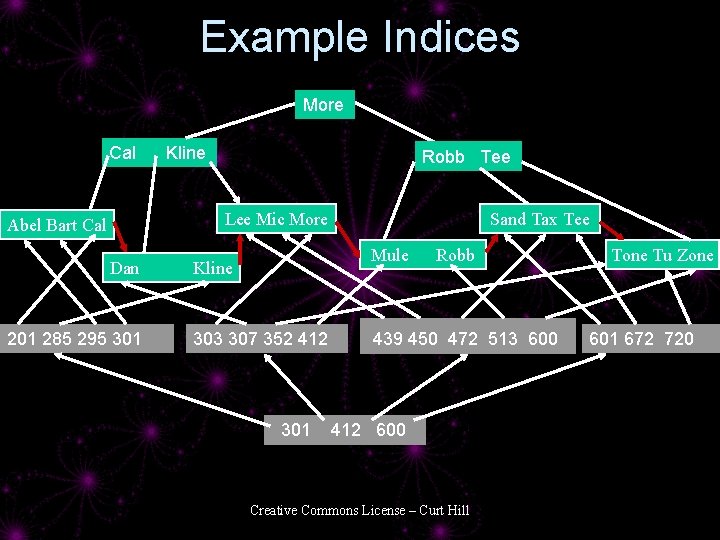
Example Indices More Cal Kline Robb Tee Lee Mic More Abel Bart Cal Dan 201 285 295 301 Sand Tax Tee Mule Kline 303 307 352 412 301 Robb 439 450 472 513 600 412 600 Creative Commons License – Curt Hill Tone Tu Zone 601 672 720

Keys • Primary keys get a clustered index • Candidate keys or non-keys usually get an unclustered index – The SQL unique attribute is used on candidate keys that are not the primary key Creative Commons License – Curt Hill

Why are BTrees Popular? • Self organizing • Any type of key • Usually flat trees – Small number of accesses • Average 75% utilization • Can be created easily Creative Commons License – Curt Hill