B Ta ng e Ci nt rc to

B: Ta ng e Ci nt rc to le th e Circular Motion B A C A ball is going around in a circle attached to a string. If the string breaks at the instant shown, which path will the ball follow? 16

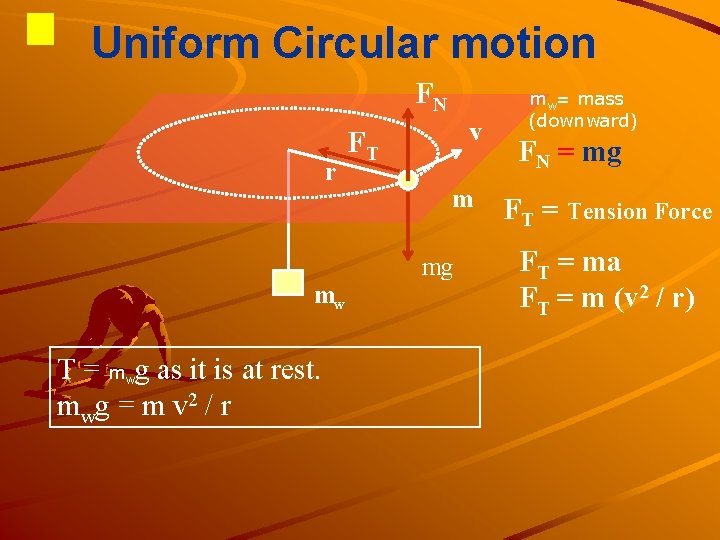
Uniform Circular motion FN r mw T = m g as it is at rest. m wg = m v 2 / r w v FT m mg mw= mass (downward) FN = mg FT = Tension Force FT = ma FT = m (v 2 / r)

Uniform Circular motion FN FT r T FT = m (v 2 / r) v mg mw What is the physical meaning of the formula? (1) What happens if the initial speed v of the bob is forced to move faster? A greater T is needed, the greater mw, to keep the radius of motion r. It will slide out to attain a greater r. (2) What happens if there is energy lost due to friction on the plane? v decreases By T = mv 2 / r, r decreases (3) What happen if an additional mass is added to the weight mw? M moves down r decreases and T increases v increases

Uniform Circular motion Uniform circular motion in a horizontal plane FT = m (v 2 / r) FN r v FTz m mg M Name 3 events as a result of a cable suddenly breaking: • • • Tension suddenly disappears and there is no more centripetal force Circular motion cannot be maintained. The bob will move with its velocity tangent to the circle at the instant the string breaks

Circular Motion Review When we see an object carrying out circular motion, we know that there must be force acting on the object, directed towards the center of the circle. When you look at the circular motion of a ball attached to a string, the force is provided by the tension in the string. When the force responsible for the circular motion disappears, e. g. by cutting the string, the motion will become linear.

Circular Motion Review 2 In most cases, the string force not only has to provide the force required for circular motion, but also the force required to balance the gravitational force.

Circular Motion and its Connection to Friction When you drive your car around a corner you carry out circular motion. In order to be able to carry out this type of motion, there must be a force present that provides the required acceleration towards the center of the circle. This required force is provided by the friction force between the tires and the road. But remember …. . The friction force has a maximum value, and there is a maximum speed with which you can make the turn. Required force = Mv 2/r. If v increases, the friction force must increase and/or the radius must increase.

Questions 2 You are driving a car with constant speed around a horizontal circular track. On a piece of paper, draw a Free Body Diagram for the car. Normal Tension How many forces are acting on the car? A) 1 B) 2 C) 3 D) 4 E) 5 3 forces, Tension (friction), gravity and the normal force The net force on the car is A. Zero B. Pointing radially inward C. Pointing radially outward Gravity B: Force of tension is pointing inward 25

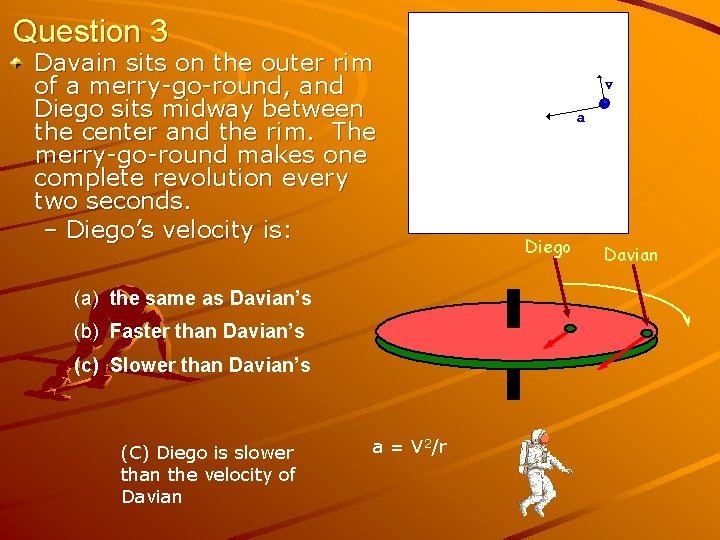
Question 3 Davain sits on the outer rim of a merry-go-round, and Diego sits midway between the center and the rim. The merry-go-round makes one complete revolution every two seconds. – Diego’s velocity is: (a) the same as Davian’s (b) Faster than Davian’s (c) Slower than Davian’s (C) Diego is slower than the velocity of Davian a = V 2/r Diego Davian

Summary Uniform Circular Motion – Speed is constant – Direction is changing – Acceleration toward center a = v 2 / r – Newton’s Second Law F = ma