B Sc H Mathematics Sem II Differential Equations

B. Sc. (H) Mathematics, Sem. II Differential Equations - 3 Practical using Mathematica 31 st March, 2020

Newton’s Law of Cooling •

Growth/Decay Model •

A certain culture of bacteria grows at a rate proportional to the number present. It is found that the number doubles in 4 hours. a) How many bacteria may be expected at the end of 24 hours? b) Draw the graph of number of bacteria versus time Initially there are 2 bacteria and k = 1. Growth Model Given f[4] = 2 f[0], f[0] = c →c e 4 k = 2 c → e 4 k = 2 → f[24] = c e 24 k = c [e 4 k]6 = c 26 = c 64 Bacteria grow 64 times in 24 hours
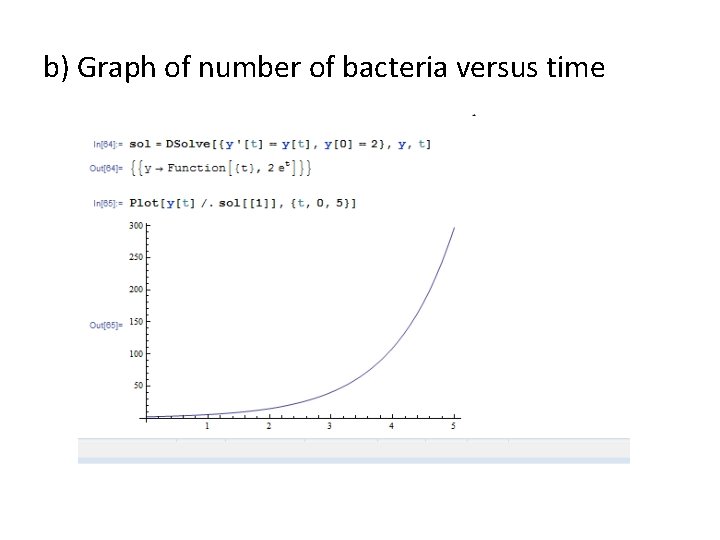
b) Graph of number of bacteria versus time

Radium decomposes at the rate proportional to the amount present. If the half the original amount disappears in 1600 years, find the percentage lost in 100 years. Given m[1600] = 1/2 f[0], f[0] = c →c e-1600 k = 1/2 c → e-1600 k = 1/2 → f[100] = c e-100 k = c [e-1600 k]1/16 = c 2 -1/16 Which is approx 96% of m , loss of 4 %

Lake Pollution model: Some Assumptions •
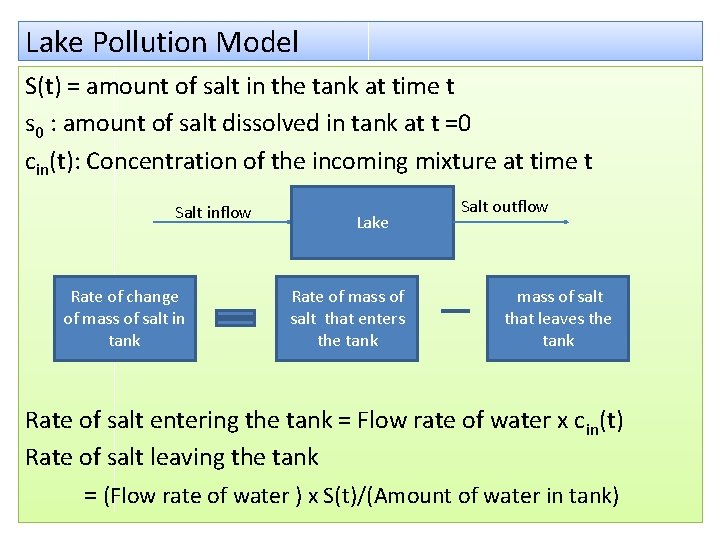
Lake Pollution Model S(t) = amount of salt in the tank at time t s 0 : amount of salt dissolved in tank at t =0 cin(t): Concentration of the incoming mixture at time t Salt inflow Rate of change of mass of salt in tank Lake Rate of mass of salt that enters the tank Salt outflow mass of salt that leaves the tank Rate of salt entering the tank = Flow rate of water x cin(t) Rate of salt leaving the tank = (Flow rate of water ) x S(t)/(Amount of water in tank)

A large tank contains 100 liters of salt water. Initially s 0 kg. of salt is dissolved. Salt water flows into the tank at the rate of 10 liters/min and the concentration cin(t) of the incoming water salt mixture varies with time. •

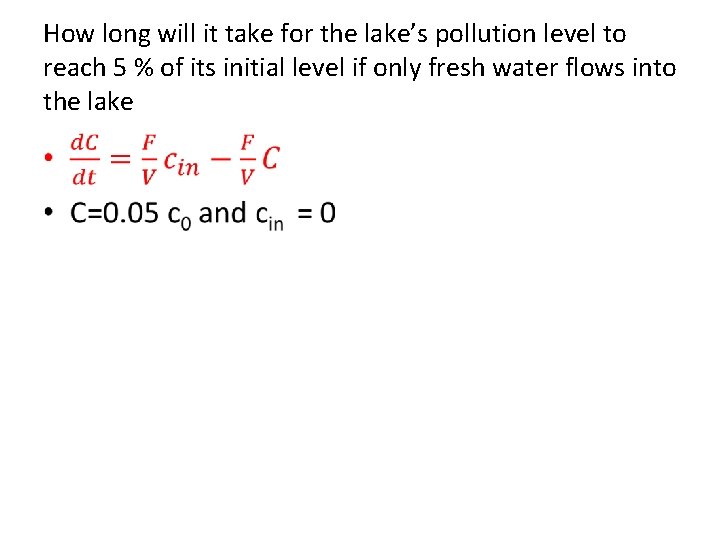
How long will it take for the lake’s pollution level to reach 5 % of its initial level if only fresh water flows into the lake •
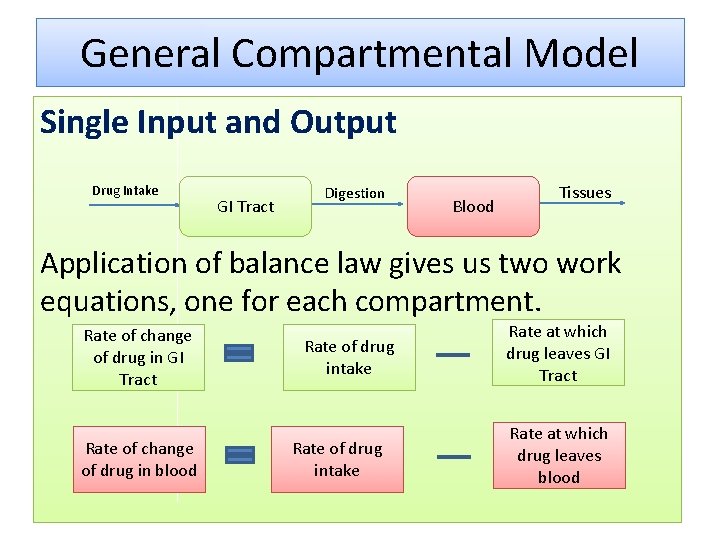
General Compartmental Model Single Input and Output Drug Intake GI Tract Digestion Blood Tissues Application of balance law gives us two work equations, one for each compartment. Rate of change of drug in GI Tract Rate of change of drug in blood Rate of drug intake Rate at which drug leaves GI Tract Rate at which drug leaves blood

Model 1 – Single Cold Pill • x(t) = amount of drug in GI tract at time t • y(t) = amount of drug in blood stream at time t • Pill is swallowed and after that for sometime there is nothing entering the GI tract. This pill diffuses in the blood stream from GI tract. So for GI tract there is only an output term. • Assume that output rate is proportional to GI tract drug concentration, which in turn is proportional to the amount of drug in the blood stream.


Suppose a single cold pill having 20 mg of drug is taken. The rate at which it diffuses in the GI tract is 1. 3 mg/hr times the amount of drug. If the amount of drug leaving the blood stream is 0. 13 mg/hr times the amount present in the blood stream. Find the amount of drug in the blood stream after 24 hours. •
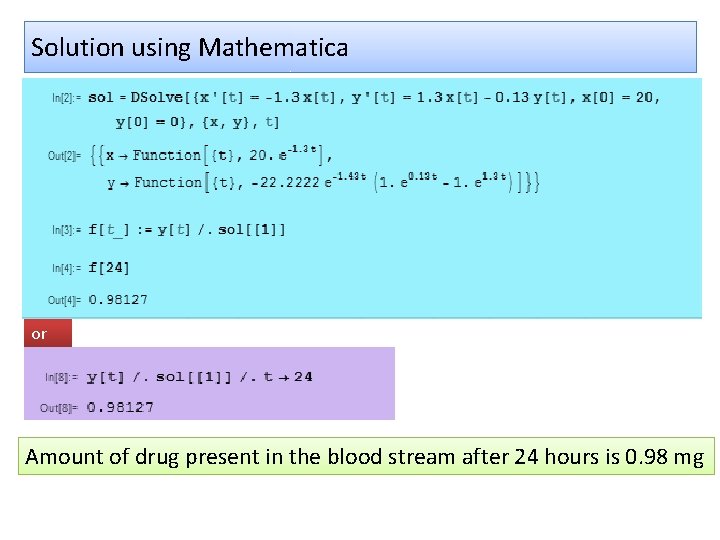
Solution using Mathematica or Amount of drug present in the blood stream after 24 hours is 0. 98 mg

Model 2 – A Course of Cold Pills • In reality particularly for a cold , we take a course of pills rather than just a single pill so that there is a continuous flow of drug into the GI track. • All the assumptions of the previous model hold except that we also assume that some amount of the drug remains indigested in the GI tract. • Let a positive constant I represent the rate of indigestion of the drug. • With slight modification in the model we get:

- Slides: 18