Axiomatic Semantics Predicate Transformers cs 7100Prasad L 18

Axiomatic Semantics Predicate Transformers cs 7100(Prasad) L 18 -9 WP 1

Motivation Input Output • Problem Specification • Properties satisfied by the input and expected of the output (usually described using “assertions”). • E. g. , Sorting problem – Input : Sequence of numbers – Output: Permutation of input that is ordered. • Program • Transform input to output. cs 7100(Prasad) L 18 -9 WP 2

• Sorting algorithms » » Bubble sort; Shell sort; Insertion sort; Selection sort; Merge sort; Quick sort; Heap sort; • Axiomatic Semantics To show that a program satisfies its specification, it is convenient to have a description of the language constructs in terms of assertions characterizing the input and the corresponding output states. cs 7100(Prasad) L 18 -9 WP 3

cs 7100(Prasad) L 18 -9 WP 4

q p cs 7100(Prasad) L 18 -9 WP 5

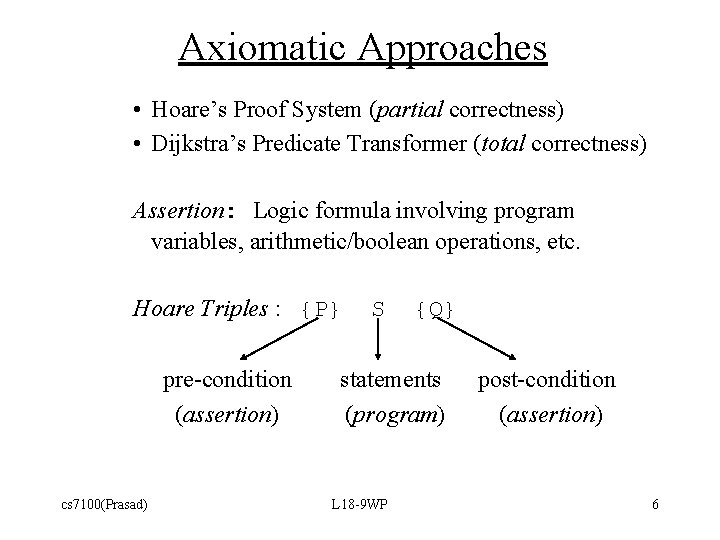
Axiomatic Approaches • Hoare’s Proof System (partial correctness) • Dijkstra’s Predicate Transformer (total correctness) Assertion: Logic formula involving program variables, arithmetic/boolean operations, etc. Hoare Triples : {P} pre-condition (assertion) cs 7100(Prasad) S {Q} statements (program) L 18 -9 WP post-condition (assertion) 6

Swap Example { x = n and y = m } t : = x; x : = y; y : = t; { x = m and y = n } – program variables vs ghost/logic variables • States : Variables -> Values • Assertions : States -> Boolean (= Powerset of States) cs 7100(Prasad) L 18 -9 WP 7

Partial vs Total Correctness {P} S {Q} • S is partially correct for P and Q if and only if whenever S is executed in a state satisfying P and the execution terminates, then the resulting state satisfies Q. • S is totally correct for P and Q if and only if whenever S is executed in a state satisfying P , then the execution terminates, and the resulting state satisfies Q. cs 7100(Prasad) L 18 -9 WP 8

Examples • Totally correct (hence, partially correct) • { • { x = 11 } x : = 0; { x = 0 } x : = x + 1; { x = 1 } false } x : = 0; { x = 111 } false } while true do; { x = 0 } • { y = 0 } if x <> y then x: = y; { x = 0 } • Not totally correct, but partially correct • { true } while true do; { x = 0} • Not partially correct • { true } if x < 0 then x: = -x; { x > 0 } cs 7100(Prasad) L 18 -9 WP 9

Axioms and Inference Rules • Assignment axiom {Q[e]} x : = e; {Q[x]} • Inference Rule for statement composition {P} S 1 {R} S 2 {Q} {P} S 1; S 2 {Q} • Example {x = y} x : = x+1; {x = y+1} y : = y+1; {x = y} x: =x+1; y: =y+1; {x = y} cs 7100(Prasad) L 18 -9 WP 10

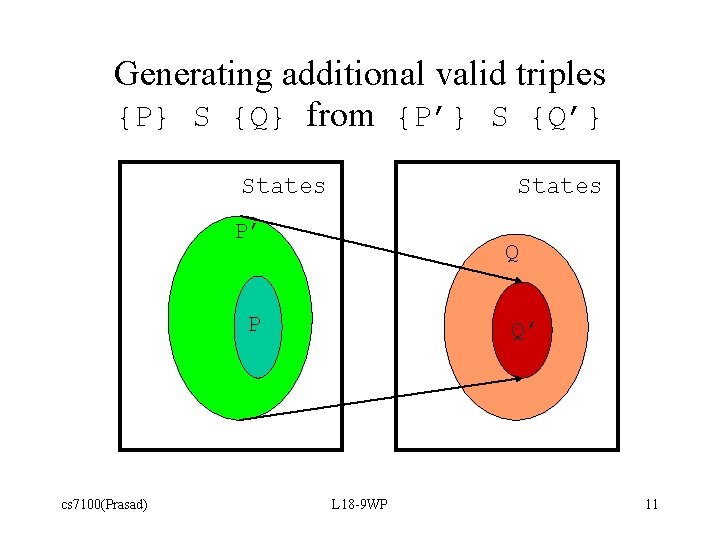
Generating additional valid triples {P} S {Q} from {P’} S {Q’} States P’ P’ cs 7100(Prasad) Q P Q’ L 18 -9 WP 11

Rule of Consequence {P’} S {Q’} and P=>P’ and Q’=>Q {P} S {Q} – – Strengthening the antecedent Weakening the consequent • Example {x=0 and y=0} x: =x+1; y: =y+1; {x = y} {x=y} x: =x+1; y: =y+1; {x<=y or x=5} (+ Facts from elementary mathematics [boolean algebra + arithmetic] ) cs 7100(Prasad) L 18 -9 WP 12

Predicate Transformers • Assignment wp( x : = e , Q ) = Q[x<-e] • Composition wp( S 1 ; S 2 , Q) = wp( S 1 , wp( S 2 , Q )) • Correctness {P} S {Q} = (P => wp( S , Q)) cs 7100(Prasad) L 18 -9 WP 13

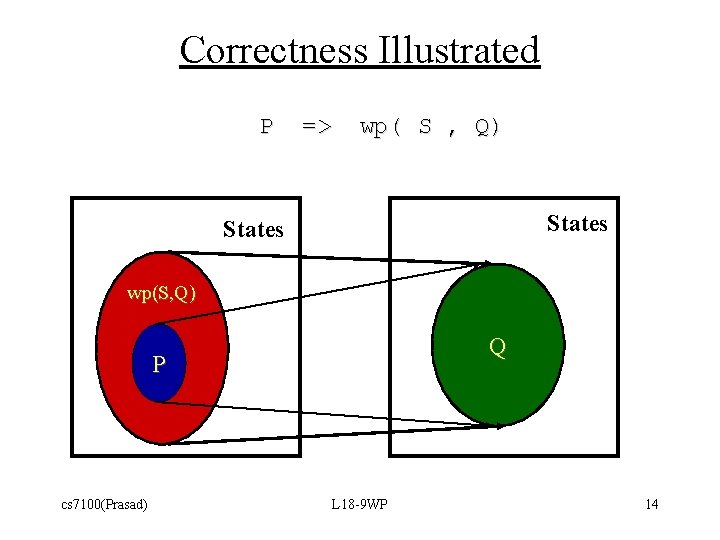
Correctness Illustrated P => wp( S , Q) States wp(S, Q) Q P cs 7100(Prasad) L 18 -9 WP 14

Correctness Proof {x=0 and y=0} x: =x+1; y: =y+1; {x = y} • wp(y: =y+1; , {x = y}) = { x = y+1 } • wp(x: =x+1; , {x = y+1}) = { x+1 = y+1 } • wp(x: =x+1; y: =y+1; , {x = y}) = { x+1 = y+1 } = { x = y } • { x = 0 and y = 0 } => { x = y } cs 7100(Prasad) L 18 -9 WP 15

Conditionals { P and B } S 1 {Q} {P and not B } S 2 {Q} {P} if B then S 1 else S 2; {Q} wp(if B then S 1 else S 2; , Q) = (B => wp(S 1, Q)) and (not B => wp(S 2, Q)) = (B and wp(S 1, Q)) or (not B and wp(S 2, Q)) cs 7100(Prasad) L 18 -9 WP 16

“Debugging” Program {true} if x < 0 then x: = -x; { x > 0 } {x < 0} x: = -x; { x > 0 } {x >= 0} ; { x > 0 } (x < 0) => (-x > 0) Because (x < 0) (0 < -x) (x >= 0) => (x > 0) (x = 0) => (x > 0) cs 7100(Prasad) L 18 -9 WP 17

“Invariant”: Summation Program { s = i * (i i : = i + s : = s + = i * (i + 1) / 2 } 1; i; + 1) / 2 } • Intermediate Assertion ( s and i different) { s + i = i * (i + 1) / 2 } • Weakest Precondition { s+i+1 = (i+1) * (i+1+1) / 2 } cs 7100(Prasad) L 18 -9 WP 18

while-loop : Hoare’s Approach {Inv and B} S {Inv} while B do S {Inv and not B} Proof of Correctness {P} while B = P => Inv and {Inv and + cs 7100(Prasad) do S {Q} and {Inv} B} S {Inv} not B => Q} Loop Termination argument L 18 -9 WP 19

{I} while B do S {I and not B} {I and B} 0 iterations: S {I} {I and not B} {I} not B holds 1 iteration: {I} B holds 2 iterations: {I} {I and not B} S not B holds S ; B holds S {I and not B} not B holds • Infinite loop if B never becomes false. cs 7100(Prasad) L 18 -9 WP 20

Example 1 : while-loop correctness { n>0 and x=1 and y=1} while (y < n) [ y++; x : = x*y; ] {x = n!} • Choice of Invariant • {I and not B} => Q • {I and (y >= n)} => (x = n!) • I = {(x = y!) and (n >= y)} • Precondition implies invariant { n>0 and x=1 and y=1} => { 1=1! and n>=1 } cs 7100(Prasad) L 18 -9 WP 21

• Verify Invariant {I and B} => wp(S, I) wp( y++; x: =x*y; , {x=y! and n>=y}) = { x=y! and n>=y+1 } I and B = { x=y! and n>=y } and { y<n } = { x=y! and n>y } • Termination • Variant : ( n - y ) y : 1 -> 2 -> … -> n (n-y) : (n-1) -> (n-2) -> … -> 0 cs 7100(Prasad) L 18 -9 WP 22

Detailed Working wp( y++; x: =x*y; , {x=y! and n>=y}) = wp(y++, {x*y=y! and n>=y}) = wp(y++, {x=y-1! and n>=y}) = {x=y+1 -1! and n>=y+1} = {x=y! and n>y} cs 7100(Prasad) L 18 -9 WP 23

GCD/HCF code PRE: (x = n) and (y = m) • while (x <> y) do ASSERT: (** INVARIANT **) • begin • if x > y then x : = x - y; • else y : = y - x; • end; POST: (x = gcd(n, m)) cs 7100(Prasad) L 18 -9 WP 24

GCD-LCM code PRE: (x = n) and (y = m) • u : = x; v : = y; • while (x <> y) do ASSERT: (** INVARIANT **) • begin • if x > y then x : = x - y; u : = u + v • else y : = y - x; v : = v + u • end; POST: (x = gcd(n, m)) and (lcm (n, m) = (u+v) div 2) cs 7100(Prasad) L 18 -9 WP 25

while-loop : Dijkstra’s Approach wp( while B do S , Q) = P 0 or P 1 or … or Pn or … = there exists k >= 0 such that Pk Pi : Set of states causing i-iterations of while-loop P 0 P 1 Pk+1 cs 7100(Prasad) before halting in a state in = = = Q. not B and Q B and wp(S, P 0) B and wp(S, Pk) L 18 -9 WP 26

States . . . wp Q P 2 P 0 P 1 P 0 => P 0 P 1 cs 7100(Prasad) wp(skip, Q) subset => Q wp(S, P 0) L 18 -9 WP 27

Example 2 : while-loop correctness P 0 Pk P 1 Pk = = { y >= n and x = n! } B and wp(S, Pk-1) { y<n and y+1>=n and x*(y+1) = n! } y=n-k and x=(n-k)! Weakest Precondition Assertion: Wp = there exists k >= 0 such that P 0 or {y = n-k and x = (n-k)!} Verification : P = n>0 and x=1 and y=1 For i = n-1: P => Wp cs 7100(Prasad) L 18 -9 WP 28

Induction Proof Hypothesis : Pk = {y=n-k and x=(n-k)!} Pk+1 = { B and wp(S, Pk) } = y<n and (y+1 = n-k) and (x*(y+1)=(n-k)!) = y<n and (y = n-k-1) and (x = (n-k-1)!) = y<n and (y = n- k+1) and (x = (n- k+1)!) = (y = n - k+1) and (x = (n - k+1)!) Valid preconditions: – { n = 4 and y = 2 and x = 2 } – { n = 5 and x = 5! and y = 6} cs 7100(Prasad) L 18 -9 WP (k = 2) (no iteration) 29