Axiomatic semantics Points to discuss The assignment statement

Axiomatic semantics Points to discuss: • • • The assignment statement Statement composition The "if-then-else" statement The "while" statement Narrowing and widening Termination Two diversions The greatest common divisor The "if-then" statement CSI 3120, Axiomatic Semantics, page 1

Program verification includes two steps. 1. Associate a formula with every meaningful step of the computation. 2. Show that the final formula logically follows from the initial one through all intermediate steps and formulae. CSI 3120, Axiomatic Semantics, page 2

What is axiomatic semantics? • Axiomatic semantics of assignments, compound statements, conditional statements, and iterative statements has been developed by Professor C. A. R. Hoare. • The elementary building blocks are the formulae for assignments and conditions. • The effects of other statements are described by inference rules that combine formulae for assignments (just as statements themselves are combinations of assignments and conditions). CSI 3120, Axiomatic Semantics, page 3

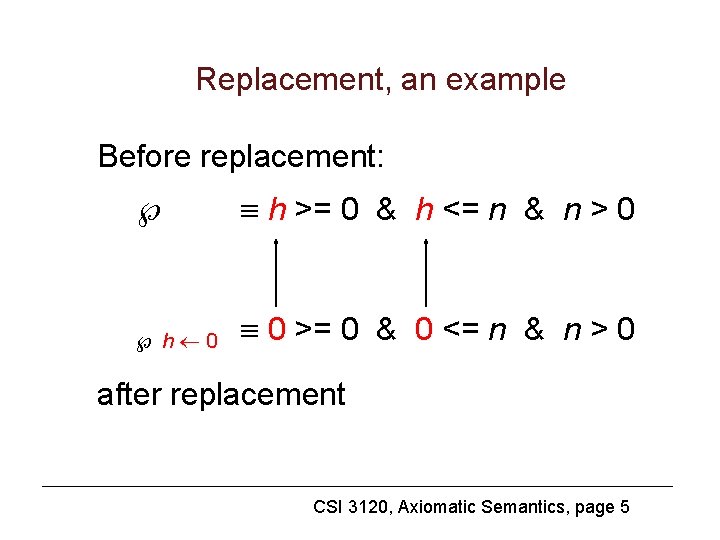
The assignment statement Let be a logical formula that contains variable v. v e is a formula which we get from when we replace all occurrences of variable v with expression e. CSI 3120, Axiomatic Semantics, page 4

Replacement, an example Before replacement: h >= 0 & h <= n & n > 0 h 0 0 >= 0 & 0 <= n & n > 0 after replacement CSI 3120, Axiomatic Semantics, page 5

Another example m == min( 1 <= i & i <= k– 1: ai ) & k– 1 <= N k k+1 m == min( 1 <= i & i <= (k+1) – 1: ai ) & (k+1)– 1 <= N m == min( 1 <= i & i <= k: ai ) & k <= N CSI 3120, Axiomatic Semantics, page 6

The axiom for the assignment statement { v e } v = e { } Example: { 0 >= 0 & 0 <= n & n > 0 } x = 0; { x >= 0 & x <= n & n > 0 } CSI 3120, Axiomatic Semantics, page 7

Two small puzzles { ? ? ? } z = z + 1; { z <= N } { a > b } a = a – b; { ? ? ? } CSI 3120, Axiomatic Semantics, page 8

Statement composition ASSUME THAT { ´ } S ´ { ´´ } and { ´´ } S ´´ { ´´´ } CONCLUDE THAT { ´ } S ´´ { ´´´ } In other words: { ´ } S ´ { ´´ } S ´´ { ´´´ } CSI 3120, Axiomatic Semantics, page 9

A more complicated example x = 0; f = 1; while (x != n) { x = x + 1; f = f * x; } We want to prove that { f == x! } x = x + 1; f = f * x; { f == x! } CSI 3120, Axiomatic Semantics, page 10

The factorial Let's apply the inference rule for composition. ´ is f == x! ´´´ is f == x! S ´ is x = x + 1; S ´´ is f = f * x; CSI 3120, Axiomatic Semantics, page 11

The factorial (2) We need to find a ´´ for which we can prove: { f == x! } x = x + 1; { ´´ } f = f * x; { f == x! } Observe that f == x! f == ((x + 1) – 1)! and therefore f == (x – 1)! x x + 1 f == x! That is: { f == x! } x = x + 1; {f == (x – 1)! } ´ S ´ ´´ CSI 3120, Axiomatic Semantics, page 12

The factorial (3) Now, let us observe that f == (x – 1)! f * x == (x – 1)! * x == x! So, we have f == x! f f * x f == (x – 1)! That is, {f == (x – 1)! } f = f * x; {f == x! } ´´ S ´´ ´´´ QED CSI 3120, Axiomatic Semantics, page 13

The "if-else" statement ASSUME THAT { & } S´ { } and { & } S´´ { } CONCLUDE THAT { } if ( ) S ´ else S ´´ { } Both paths through the if-else statement establish the same fact . That is why the whole conditional statement establishes this fact. CSI 3120, Axiomatic Semantics, page 14

"if-else", an example The statement if ( a < 0 ) b = -a; else b = a; makes the formula b == abs(a) true. Specifically, the following fact holds: {true} if ( a < 0 ) b = -a; else b = a; { b == abs(a) } Here: is true is b == abs(a) is a < 0 Also: S´ is b = -a; S´´ is b = a; CSI 3120, Axiomatic Semantics, page 15

"if-else", an example (2) We will consider cases. First, we assume that is true: true & a < 0 – a == abs(a) Therefore, by the assignment axiom: {– a == abs(a)} b = -a; {b == abs(a)} Similarly, when we assume , we get this: true & a < 0 a 0 a == abs(a) Therefore: {a == abs(a)} b = a; {b == abs(a)} CSI 3120, Axiomatic Semantics, page 16

"if-else", an example (3) This shows that both S´ and S´´ establish the same condition: b == abs(a) Our fact has been proven: {true} if ( a < 0 ) b = -a; else b = a; { b == abs(a) } In other words, our conditional statement computes abs(a). It does so without any preconditions: "true" means that there are no restrictions on the initial values of a and b. CSI 3120, Axiomatic Semantics, page 17

The "while" statement A loop invariant is a condition that is true immediately before entering the loop, stays true during its execution, and is still true after the loop has terminated. ASSUME THAT { & } S { } [That is, S preserves . ] CONCLUDE THAT { } while ( ) S { & } provided that the loop terminates. CSI 3120, Axiomatic Semantics, page 18

The factorial again. . . x = 0; f = 1; while ( x != n ) { x = x + 1; f = f * x; } Assume that n ≥ 0. After computing x = 0; f = 1; we have f == x! because it is true that 1 == 0! CSI 3120, Axiomatic Semantics, page 19

The factorial again. . . (2) We showed earlier that { f == x! } x = x + 1; f = f * x; { f == x! } The reasoning will not change if we add the condition n ≥ 0, because the transitions do not depend on n. So, we can write { n ≥ 0 & f == x! } x = x + 1; f = f * x; { n ≥ 0 & f == x! } CSI 3120, Axiomatic Semantics, page 20

The factorial again. . . (3) Now, is is is f == x! x != n x == n Using the inference rule for "while" loops: { n ≥ 0 & f == x! } while ( x != n ) { x = x + 1; f = f * x; } { n ≥ 0 & f == x! & x == n } CSI 3120, Axiomatic Semantics, page 21

The factorial again. . . (4) Notice that f == x! & x == n f == n! This means two things: { n ≥ 0 } x = 0; f = 1; { n ≥ 0 & f == x! } AND { n ≥ 0 & f == x! } while ( x != n ) { x = x + 1; f = f * x; } { n ≥ 0 & f == n! } CSI 3120, Axiomatic Semantics, page 22

The factorial again. . . (5) In other words, the program establishes f == n! without any preconditions on the initial values of f and n, assuming that we only deal with n ≥ 0. The axiom for statement composition gives us: { n ≥ 0 } x = 0; f = 1; while ( x != n ) { x = x + 1; f = f * x; } { f == n! } So: this program does compute the factorial of n. CSI 3120, Axiomatic Semantics, page 23

The factorial again. . . (6) Our reasoning agrees with the intuition of loop invariants: we adjust some variables and make the invariant temporarily false, but we re-establish it by adjusting some other variables. { f == x! } x = x + 1; { f == (x – 1)! } the invariant is "almost true" { f == (x – 1)! } f = f * x; { f == x! } the invariant is back to normal This reasoning is not valid for infinite loops: the terminating condition & is never reached, and we know nothing of the situation following the loop. CSI 3120, Axiomatic Semantics, page 24

Narrowing and widening ASSUME THAT ´ and { } S { } ASSUME THAT { } S { } and ´ CONCLUDE THAT { ´ } S { } { } S { ´ } These rules can be used to narrow a precondition, or to widen a postcondition. CSI 3120, Axiomatic Semantics, page 25

Narrowing and widening, a small example n! is computed, for any nonnegative n, with true as the precondition (it is always computed successfully); So, n! will in particular must be computed successfully if initially n == 5. CSI 3120, Axiomatic Semantics, page 26

A larger example (in a more concise notation) { N >= 1 } { N >= 1 & 1 == 1 & a 1 == a 1 } i = 1; s = a 1; { N >= 1 & i == 1 & s == a 1 } { N >= 1 & s == a 1 + … + ai } while ( i != N ) { INVARIANT { N >= 1 & s == a 1 + … + ai & i != N } i = i + 1; { N >= 1 & s == a 1 + … + ai– 1 & i – 1 != N } s = s + ai; } { N >= 1 & s == a 1 + … + ai & i == N } { N >= 1 & s == a 1 + … + a. N } CSI 3120, Axiomatic Semantics, page 27

A larger example (2) • We have shown that this program computes the sum of a 1, . . . , a. N. • The precondition N >= 1 is only necessary to prove termination. CSI 3120, Axiomatic Semantics, page 28

Termination • Proofs like these show only partial correctness. – Everything is fine if the loop stops. – Otherwise we don't know (but the program may be correct for most kinds of data). • A reliable proof must show that all loops in the program are finite. • We can prove termination by showing how each step brings us closer to the final condition. CSI 3120, Axiomatic Semantics, page 29

Once again, the factorial… • Initially, x == 0. • Every step increases x by 1, so we go through the numbers 0, 1, 2, . . . • n >= 0 must be found among these numbers. • Notice that this reasoning will not work for n < 0: the program loops. CSI 3120, Axiomatic Semantics, page 30

A decreasing function • A loop terminates when the value of some function of program variables goes down to 0 during the execution of the loop. • For the factorial program, such a function could be n – x. Its value starts at n and decreases by 1 at every step. • For summation, we can take N – i. CSI 3120, Axiomatic Semantics, page 31

Multiplication by successive additions { B >= 0 & B == B & 0 == 0} FOR TERMINATION b = B; p = 0; { b == B & p == 0 } { p == A * (B – b) } INVARIANT while ( b != 0 ) { p = p + A; { p == A * (B – (b – 1)) } b = b - 1; { p == A * (B – b) } } { p == A * (B – b) & b == 0} { p == A * B } The loop terminates, because the value of the variable b goes down to 0. CSI 3120, Axiomatic Semantics, page 32

Two diversions Prove that the sequence p = a; a = b; b = p; exchanges the values of a and b : { a == A & b == B } p = a; a = b; b = p; { b == A & a == B } The highlights of a proof: { a == A & b == B } { p == A & a == B } { b == A & a == B } p = a; a = b; b = p; CSI 3120, Axiomatic Semantics, page 33

Two diversions (2) Discover and PROVE the behaviour of the following sequence of statements for integer variables x, y: x = x + y; y = x - y; x = x - y; CSI 3120, Axiomatic Semantics, page 34

Two diversions (3) {x == X & y == Y } {x + y == X + Y & y == Y } x = x + y; {x == X + Y & y == Y } {x == X + Y & x - y == X } y = x - y; {x == X + Y & y == X } { x - y == Y & y == X } x = x - y; { x == Y & y == X } CSI 3120, Axiomatic Semantics, page 35

The greatest common divisor { X > 0 & Y > 0 } a = X; b = Y; { } what should the invariant be? while ( a != b ) { & a != b } { if ( a > b ) { & a != b & a > b } a = a - b; else { & a != b & (a > b) } b = b - a; } { & (a != b) } { GCD( X, Y ) == a } CSI 3120, Axiomatic Semantics, page 36

GCD (2) We will need only a few properties of greatest common divisors: GCD( n + m, m ) == GCD( n, m ) GCD( n, m + n ) == GCD( n, m ) The first step (very formally): { X > 0 & Y > 0 } { X > 0 & Y > 0 & X == X & Y == Y } a = X; b = Y; { a > 0 & b > 0 & a == X & b == Y } CSI 3120, Axiomatic Semantics, page 37

GCD (3) When the loop stops, we get a == b & GCD( a, b ) == a We may want this condition in the invariant: a == b & GCD( X, Y ) == GCD( a, b ) At the beginning of the loop, we have: { a > 0 & b > 0 & a == X & b == Y } {a > 0 & b > 0 & GCD( X, Y ) == GCD( a, b ) } So, the invariant could be this: a > 0 & b > 0 & GCD( X, Y ) == GCD( a, b ) CSI 3120, Axiomatic Semantics, page 38

GCD (4) We should be able to prove that {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b) & a != b} while. . . {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b)} The final condition will be a > 0 & b > 0 & GCD(X, Y) == GCD(a, b) & a == b and this will imply GCD( X, Y ) == a CSI 3120, Axiomatic Semantics, page 39

GCD (5) The loop consists of one conditional statement. Our proof will be complete if we show this: {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b) & a != b} if ( a > b ) a = a - b; else b = b - a; {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b)} CSI 3120, Axiomatic Semantics, page 40

GCD (6) Consider first the case of a > b. {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b) & a != b & a > b } {a – b > 0 & GCD(X, Y) == GCD(a – b, b)} a = a - b; {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b)} CSI 3120, Axiomatic Semantics, page 41

GCD (7) Now, the case of a > b. {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b) & a != b & (a > b) } {a > 0 & b – a > 0 & GCD(X, Y) == GCD(a, b – a)} b = b - a; {a > 0 & b > 0 & GCD(X, Y) == GCD(a, b)} CSI 3120, Axiomatic Semantics, page 42

GCD (8) Both branches of if-else give the same final condition. We will complete the correctness proof when we show that the loop terminates. We show the value of max( a, b ) decreases at each turn of the loop. Let a == A, b == B at the beginning of a step. Assume first that a > b: max( a, b ) == A, so a – b < A, therefore max( a – b, b ) < A. CSI 3120, Axiomatic Semantics, page 43

GCD (9) Now assume that a < b: max( a, b ) == B, b – a < B, therefore max( a, b – a ) < B. Since a > 0 and b > 0, max( a, b ) > 0. This means that decreasing the values of a, b cannot go forever. QED CSI 3120, Axiomatic Semantics, page 44

The "if" statement ASSUME THAT { & } S { } and & CONCLUDE THAT { } if ( ) S { } CSI 3120, Axiomatic Semantics, page 45

An example with "if" We will show the following: { N > 0 } k = 1; m = a 1; while ( k != N ) { k = k + 1; if ( ak < m ) m = ak; } { m == min( 1 <= i & i <= N: ai ) } CSI 3120, Axiomatic Semantics, page 46

Minimum Loop termination is obvious: the value of N – k goes down to zero. Here is a good invariant: at the kth turn of the loop, when we have already looked at a 1, . . . , ak, we know that m == min( 1 <= i & i <= k : ai ). Initially, we have this: { N > 0 } k = 1; m = a 1; { k == 1 & m == a 1 } { k == 1 & m == min( 1 <= i & i <= k : ai ) } CSI 3120, Axiomatic Semantics, page 47

Minimum We must prove the following: { m == min( 1 <= i & i <= k : ai ) & k != N } k = k + 1; if ( ak < m ) m = ak; { m == min( 1 <= i & i <= k : ai ) } CSI 3120, Axiomatic Semantics, page 48

Minimum (2) { m == min( 1 <= i & i <= k : ai ) & k != N } { m == min( 1 <= i & i <= (k + 1) – 1: ai ) & (k + 1) – 1 != N } k = k + 1; { m == min( 1 <= i & i <= k – 1: ai ) & k – 1 != N } Note that k – 1 != N ensures the existence of ak. CSI 3120, Axiomatic Semantics, page 49

Minimum (3) This remains to be shown: { m == min( 1 <= i & i <= k – 1: ai ) & k – 1 != N } if ( ak < m ) m = ak; { m == min( 1 <= i & i <= k: ai ) } The fact we will use is this: min( 1 <= i & i <= k: ai ) == min 2( min( 1 <= i & i <= k – 1: ai ), ak ) CSI 3120, Axiomatic Semantics, page 50

Minimum (4) We will consider two cases of the conditional statement. First, (ak < m). {m == min(1 <= i & i <= k – 1: ai ) & k – 1 != N & (ak < m)} {m == min 2(min( 1 <= i & i <= k – 1: ai ), ak )} {m == min(1 <= i & i <= k: ai )} CSI 3120, Axiomatic Semantics, page 51

Minimum (5) Now, ak < m. {m == min(1 <= i & i <= k – 1: ai ) & k – 1 != N & ak < m} {ak == min 2( min( 1 <= i & i <= k – 1: ai ), ak )} {ak == min(1 <= i & i <= k: ai )} m = ak; {m == min(1 <= i & i <= k: ai )} So, the body of the loop preserves the condition m == min( 1 <= i & i <= k: ai ) CSI 3120, Axiomatic Semantics, page 52

Minimum (6) Now, the whole loop works as follows: { m == min( 1 <= i & i <= k: ai ) } while ( k != N ) } k = k + 1; if ( ak < m ) ak = m; } { m == min( 1 <= i & i <= k: ai ) & k == N } { m == min( 1 <= i & i <= N: ai ) } All in all, we have shown that our program finds the minimum of N numbers, if only N > 0. QED CSI 3120, Axiomatic Semantics, page 53

Examples Yet another "while" loop { B > 0 } FOR TERMINATION b = 1; p = A; while ( b != B ) { b = b + 1; p = p * A; } { ? ? ? } CSI 3120, Axiomatic Semantics, page 54

Examples Yet another "while" loop (2) { B > 0 & 1 == 1 & A == A} FOR TERMINATION b = 1; p = A; { b == 1 & p == A } { p == A ** b } INVARIANT while ( b != B ) { b = b + 1; { p == A ** (b - 1) } p = p * A; { p == A ** b } } { p == A ** b & b == B} { p == A ** B } The loop terminates: the value B - b goes down to 0. CSI 3120, Axiomatic Semantics, page 55

Examples Another example with "if" { N > 0 } FOR TERMINATION k = 1; while ( k != N ) { if ( Ak > Ak+1 ) { p = Ak; Ak = Ak+1; Ak+1 = p; } k = k + 1; } { ? ? ? } CSI 3120, Axiomatic Semantics, page 56

Examples Another example with "if" (2) { N > 0 } FOR TERMINATION k = 1; { Ak == max( 1 <= i & i <= k: Ai ) } INVARIANT while ( k != N ) { { Ak == max( 1 <= i & i <= k: Ai ) & k != N } if ( Ak > Ak+1 ) { p = Ak; Ak = Ak+1; Ak+1 = p; } { Ak+1 == max( 1 <= i & i <= k+1: Ai ) } k = k + 1; { Ak == max( 1 <= i & i <= k: Ai ) } } {Ak == max( 1 <= i & i <= k: Ai ) & k == N } {AN == max( 1 <= i & i <= N: Ai ) } CSI 3120, Axiomatic Semantics, page 57

Examples Another example with "if" (3) {Ak == max( 1 <= i & i <= k: Ai ) & k != N } case 1: Ak > Ak+1 { Ak == max( 1 <= i & i <= k: Ai ) & k != N & Ak > Ak+1} p = Ak; { p > Ak+1 } Ak = Ak+1; { p > Ak } Ak+1 = p; { Ak+1 > Ak } { Ak+1 == max( 1 <= i & i <= k+1: Ai ) } case 2: Ak <= Ak+1 { Ak == max( 1 <= i & i <= k: Ai ) & k != N & Ak <= Ak+1 } { Ak+1 == max( 1 <= i & i <= k+1: Ai ) } CSI 3120, Axiomatic Semantics, page 58