Axiomatic Semantics Hoares Correctness Triplets Dijkstras Predicate Transformers

Axiomatic Semantics Hoare’s Correctness Triplets Dijkstra’s Predicate Transformers

gcd-lcm algorithm w/ invariant {PRE: (x = n) and (y = m)} u : = x; v : = y; while {INV: 2*m*n = x*v + y*u} (x <> y) do if x > y then x : = x - y; u : = u + v else y : = y - x; v : = v + u fi od {POST: (x = gcd(m, n)) and (lcm(m, n) = (u+v) div 2)} cs 784(tk/pm) 2

Goal of a program = IO Relation • Problem Specification – Properties satisfied by the input and expected of the output (usually described using “assertions”). – E. g. , Sorting problem • Input : Sequence of numbers • Output: Permutation of input that is ordered. • View Point – All other properties are ignored. • Timing behavior • Resource consumption • … cs 784(tk/pm) 3

ax·i·om • n. 1. A self-evident or universally recognized truth; a maxim • 2. An established rule, principle, or law. • 3. A self-evident principle or one that is accepted as true without proof as the basis for argument; a postulate. • From a dictionary cs 784(tk/pm) 4

Axiomatic Semantics • Capture the semantics of the elements of the PL as axioms • Capture the semantics of composition as a rule of inference. • Apply the standard rules/logic of inference. • Consider termination separately. cs 784(tk/pm) 5

States and Assertions • States: Variables mapped to Values – Includes all variables – Files etc. are considered “global” variables. – No notion of value-undefined variables – At a given moment in execution • An assertion is a logic formula involving program variables, arithmetic/boolean operations, etc. • All assertions are attached to a control point. • Assertions: States mapped to Boolean – Boolean connectives: and, or, not, implies, … – For-all, There-exists – Special predicates defined just for use in assertions (not for use in the program). cs 784(tk/pm) 6

Hoare’s Logic • Hoare Triplets: {P} S {Q} – P, pre-condition assertion; S, statements of a PL; Q, post-condition assertion – If S begins executing in a state satisfying P, upon completion of S, the resulting state satisfies Q. – {P} S {Q} has no relevance if S is begun otherwise. • A Hoare triplet is either true or false. Never undefined. • The entire {P}S{Q} is considered true if the resulting state satisfies Q if and when S terminates. • If not, the entire {P}S{Q} is false. cs 784(tk/pm) 7

Hoare Triplet Examples • • true triplets – {x = 11 } x : = 0 { x = 0 } • we can give a weaker precondition – {x = 0 } x : = x + 1 { x = 1 } – {y = 0} if x <> y then x: = y fi { x = 0 } – {false } x : = 0 { x = 111 } • correct because “we cannot begin” – no state satisfies false • post condition can be any thing you dream – {true} while true do od {x = 0} • true is the weakest of all predicates • correct because control never reaches post – {false} while true do od {x = 0} • false is the strongest of all predicates false triplet – {true} if x < 0 then x: = -x fi { x > 0 } cs 784(tk/pm) 8

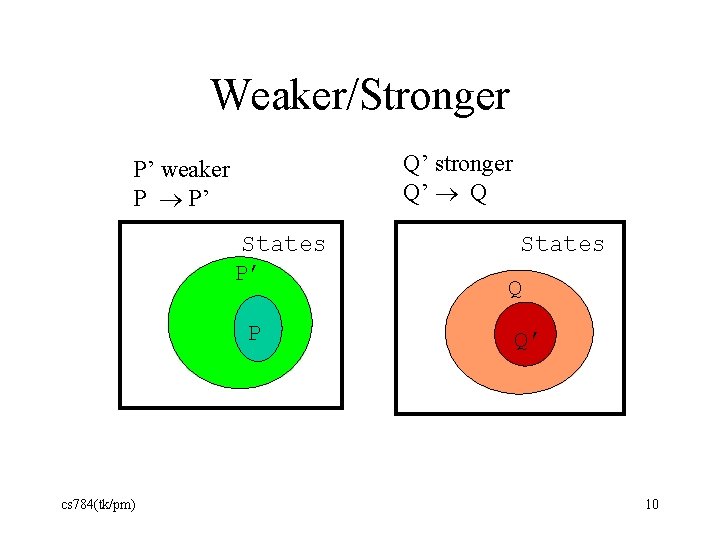
Weaker/Stronger • An assertion R is said to be weaker than assertion P if – the truth of P implies the truth of R • written: P→R – equivalently • not P or R. • For arbitrary A, B we have: A and B → B – This general idea is from Propositional Calculus • n > 0 is of course weaker than n = 1, but this follows from Number Theory. cs 784(tk/pm) 9

Weaker/Stronger Q’ stronger Q’ Q P’ weaker P P’ States P’ P’ cs 784(tk/pm) P States Q Q’ 10

Partial vs Total Correctness • Are P and S such that termination is guaranteed? • S is partially correct for P and Q iff whenever the execution terminates, the resulting state satisfies Q. • S is totally correct for P and Q iff the execution is guaranteed to terminate, and the resulting state satisfies Q. cs 784(tk/pm) 11

Hoare Triplet Examples 1. Totally correct (hence, partially correct) a. b. c. d. e. {x = 11} x : = 0 {x = 0} x : = x + 1 {x = 1} {y = 0}if x <> y then x: = y fi {x = 0} {false} while true do S od {x = 0} {false} x : = 0 {x = 111} 2. Not totally correct, but partially correct – {true} while true do S od {x = 0} 3. Not partially correct – {true} if x < 0 then x: = -x fi {x > 0} cs 784(tk/pm) 12

Assignment axiom • • • {Q(e)} x : = e {Q(x)} Q(x) has free occurrences of x. Q(e): every free x in Q replaced with e Assumption: e has no side effects. Caveats – If x is not a “whole” variable (e. g. , a[2]), we need to work harder. – PL is assumed to not facilitate aliasing. cs 784(tk/pm) 13

Inference Rules • Rules are written as Hypotheses: H 1, H 2, H 3 ---------------Conclusion: C 1 • Can also be stated as: – H 1 and H 2 and H 3 implies C 1 – Given H 1, H 2, and H 3, we can conclude C 1. cs 784(tk/pm) 14

Soundness and Completeness • • Soundness is about “validity” Completeness is about “deducibililty” Ideally in a formal system, we should have both. Godel’s Incompleteness Theorem: – Cannot have both • Inference Rules ought to be sound – What we proved/ inferred/ deduced is valid • Examples of Unsound Rules – A and B and C not B – x > y implies x > y+1 (in the context of numbers) • All the rules we present from now on are sound cs 784(tk/pm) 15

Rule of Consequence • Suppose: {P’} S {Q’}, P=>P’, Q’=>Q • Conclude: {P} S {Q} • Replace – precondition by a stronger one – postcondition by a weaker one cs 784(tk/pm) 16

Statement Composition Rule {P} S 1 {R}, {R} S 2 {Q} ---------------{P} S 1; S 2 {Q} Using Rule of Consequence {P} S 1 {R 1}, R 1 R 2, {R 2} S 2 {Q} --------------{P} S 1; S 2 {Q} cs 784(tk/pm) 17

if-then-else-fi Hoare’s Triplets {P and B} S 1 {Q} {P and not B} S 2 {Q} ------------------{P} if B then S 1 else S 2 fi {Q} • We assumed that B is side-effect free – Execution of B does not alter state cs 784(tk/pm) 18

Invariants • An invariant is an assertion whose truth-value does not change • Recall: All assertions are attached to a control point. • An Example: x > y – The values of x and y may or may not change each time control reaches that point. – But suppose the > relationship remains true. – Then x > y is an invariant cs 784(tk/pm) 19

Loop Invariants • Semantics of while-loop {I and B} S {I} ---------------------{I} while B do S od {I and not B} • Termination of while-loop is not included in the above. • We assumed that B is side-effect free. cs 784(tk/pm) 20

Data Invariants • Well-defined OOP classes • Public methods ought to have a pre- and post-conditions defined • There is a common portion across all public methods • That common portion is known as the data invariant of the class. cs 784(tk/pm) 21

while-loop: Hoare’s Approach • Wish to prove: {P} while B do S od {Q} – Given: P, B, S and Q – Not given: a loop invariant I • The I is expected to be true just before testing B • To prove {P} while B do S od {Q}, discover a strong enough loop invariant I so that 1. P => I 2. {I and B} S {I} 3. I and not B => Q • We used the Rule of Consequence twice cs 784(tk/pm) 22

A while-loop example { n > 0 and x = 1 and y = 1} while (n > y) do y : = y + 1; x : = x*y od {x = n!} cs 784(tk/pm) 23

while-loop: Choose the Invariant • Invariant I should be such that – I and not B Q – I and not (n > y) (x = n!) • Choose (n ≥ y and x = y!) as our I • Precondition Invariant – n > 0 and x=1 and y=1 n ≥ 1 and 1=1! cs 784(tk/pm) 24

while-loop: Verify Invariant • I === n ≥ y and x = y! • Verify: {I and n > y} y: = y + 1; x: =x*y {I} 1. 2. 3. 4. 5. 6. cs 784(tk/pm) {I and n > y} y: = y + 1 {n ≥ y and x*y = y!} {I and n > y} y: = y + 1 {n ≥ y and x= (y-1)!} (I and n > y) (n ≥ y+1 and x= (y+1 -1)!) (I and n > y) (n > y and x= y!) (n ≥ y and x = y! and n > y) (n > y and x= y!) QED 25

while-loop: I and not B Q • • I === n ≥ y and x = y! and not (n > y) x = n! n = y and x = y! x = n! QED cs 784(tk/pm) 26

while-loop: Termination • Termination is not part of Hoare’s Triplets • General technique: – Find a quantity that decreases in every iteration. – And, has a lower bound – The quantity may or may not be computed by the algorithm • For our example: Consider n – y – values of y: 1, 2, …, n-1, n – values of n - y: n-1, n-2, …, 1, 0 cs 784(tk/pm) 27

Weakest Preconditions • We want to determine minimally what must be true immediately before executing S so that – assertion Q is true after S terminates. – S is guaranteed to terminate • The Weakest-Precondition of S is a mathematical function mapping any post condition Q to the "weakest" precondition Pw. – Pw is a condition on the initial state ensuring that execution of S terminates in a final state satisfying R. – Among all such conditions Pw is the weakest – wp(S, Q) = Pw cs 784(tk/pm) 28

Dijkstra’s wp(S, Q) • Let Pw = wp(S, Q) • Def of wp(S, Q): Weakest precondition such that if S is started in a state satisfying Pw, S is guaranteed to terminate and Q holds in the resulting state. – Consider all predicates Pi so that {Pi}S{Q}. – Discard any Pi that does not guarantee termination of S. – Among the Pi remaining, choose the weakest. This is Pw. • {P} S {Q} versus P => wp(S, Q) – {Pw} S {Q} is true. – But, the semantics of {Pw} S {Q} does not include termination. – If P => wp(S, Q) then {P}S{Q} also, and furthermore S terminates. cs 784(tk/pm) 29

Properties of wp • Law of the Excluded Miracle wp(S, false) = false • Distributivity of Conjunction wp(S, P and Q) = wp(S, P) and wp(S, Q) • Law of Monotonicity (Q→R) → (wp(S, Q)→wp(S, R)) • Distributivity of Disjunction wp(S, P) or wp(S, Q) → wp(S, P or Q) cs 784(tk/pm) 30

Predicate Transformers • Assignment wp(x : = e, Q(x)) = Q(e) • Composition wp(S 1; S 2, Q) = wp(S 1, wp(S 2, Q)) cs 784(tk/pm) 31

A Correctness Proof • {x=0 and y=0} x: =x+1; y: =y+1 {x = y} • wp(x: =x+1; y: =y+1, x = y) • wp(x: =x+1, wp(y: =y+1, x = y)) === wp(x: =x+1, x = y+1) === x+1 = y+1 === x = y • x = 0 and y = 0 x = y cs 784(tk/pm) 32

if-then-else-fi in Dijkstra’s wp wp(if B then S 1 else S 2 fi, Q) === (B wp(S 1, Q)) and (not B wp(S 2, Q)) === (B and wp(S 1, Q)) or (not B and wp(S 2, Q)) cs 784(tk/pm) 33

wp-semantics of while-loops • • • DO == while B do S od IF == if B then S fi Let k stand for the number of iterations of S Clearly, k >= 0 If k > 0, while B do S od is the same as: – if B then S fi; while B do S od cs 784(tk/pm) 34

while-loop: wp Approach • wp(DO, Q) = P 0 or there-exists k > 0: Pk • States satisfying Pi cause i-iterations of while-loop before halting in a state in Q. • Pi defined inductively – P 0 = not B and Q –… cs 784(tk/pm) 35

wp(DO, Q) • • There exists a k, k ≥ 0, such that H(k, Q) H is defined as follows H(0, Q) = not B and Q H(k, Q) = H(0, Q) or wp(IF, H(k-1, Q)) cs 784(tk/pm) 36

Example (same as before) { n>0 and x=1 and y=1} while (n > y) do y : = y + 1; x : = x*y od {x = n!} cs 784(tk/pm) 37

Example: while-loop correctness Pre === n>0 and x=1 and y=1 P 0 === y >= n and x = n! Pk === B and wp(S, Pk-1) P 1 === y > n and y+1>=n and x*(y+1) = n! Pk === y=n-k and x=(n-k)! Weakest Precondition: W === there exists k >= 0 such that P 0 or Pk Verification : For k = n-1: Pre => W cs 784(tk/pm) 38

Induction Proof • • • Hypothesis : Pk = (y=n-k and x=(n-k)!) Pk+1 = B and wp(S, Pk) = y<n and (y+1 = n-k) and (x*(y+1)=(n-k)!) = y<n and (y = n-k-1) and (x = (n-k-1)!) = y<n and (y = n- k+1) and (x = (n- k+1)!) = (y = n - k+1) and (x = (n - k+1)!) • Examples of Valid preconditions: – { n = 4 and y = 2 and x = 2 } (k = 2) – { n = 5 and x = 5! and y = 6} (no iteration) cs 784(tk/pm) 39

Detailed Work wp(y: =y+1; x: =x*y, x=y!and n>=y) = = wp(y: =y+1, x*y=y! and n>=y) wp(y: =y+1, x=(y-1)! and n>=y) x=(y+1 -1)! and n>=y+1) x=y! and n>y cs 784(tk/pm) 40

gcd-lcm algorithm w/ invariant {PRE: (x = n) and (y = m)} u : = x; v : = y; while {INV: 2*m*n = x*v + y*u} (x <> y) do if x > y then x : = x - y; u : = u + v else y : = y - x; v : = v + u fi od {POST: (x = gcd(m, n)) and (lcm(m, n) = (u+v) div 2)} cs 784(tk/pm) 41

gcd-lcm algorithm proof • PRE implies Loop Invariant – (x = n) and (y = m) implies 2*m*n = x*v + y*u • {Invariant and B} Loop-Body {Invariant} {2*n*m = x*v + y*u and x <> y} loop-body {2*n*m = x*v + y*u} • Invariant and not B implies POST 2*n*m = x*v + y*u and x == y implies (x = gcd(n, m)) and (lcm(n, m) = (u+v) div 2) cs 784(tk/pm) 42

gcd-lcm algorithm proof • Invariant and not B implies POST 2*m*n = x*v + y*u and x == y implies (x = gcd(m, n)) and (lcm(m, n) = (u+v) div 2) • Simplifying 2*m*n = x*(u + v) and x == y implies (x = gcd(m, n)) and (lcm(m, n) = (u+v) div 2) cs 784(tk/pm) 43

gcd-lcm algorithm proof • Simplifying 2*m*n = x*(u + v) and x == y implies (x = gcd(m, n)) and (x*lcm(m, n) = m*n) cs 784(tk/pm) 44

Some Properties of lcm-gcd • gcd() and lcm() are symmetric – gcd(m, n) = gcd(n, m) – lcm(m, n) = lcm(n, m) • gcd(m, n) = gcd(m + k*n, n) – where k is a natural number. • gcd(m, n) * lcm(m, n) = m * n cs 784(tk/pm) 45