Axially loaded columns Effective length Axial Load Eccentric

Axially loaded columns • Effective length • Axial Load • Eccentric load

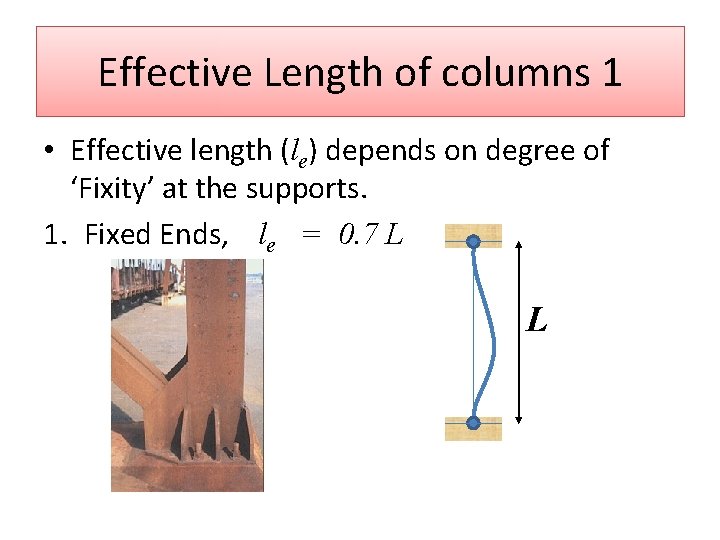
Effective Length of columns 1 • Effective length (le) depends on degree of ‘Fixity’ at the supports. 1. Fixed Ends, le = 0. 7 L L

Effective Length of columns 2 • Effective length (le) depends on degree of ‘Fixity’ at the supports. 1. One end fixed, other pinned le = 0. 85 L L

Effective Length of columns 3 • Effective length (le) depends on degree of ‘Fixity’ at the supports. 1. Pinned Ends le = L L

Effective Length of columns 4 • Effective length (le) depends on degree of ‘Fixity’ at the supports. 1. One end fixed, other end free (sway in one direction) le = 1. 5 L L

Effective Length of columns 5 • Effective length (le) depends on degree of ‘Fixity’ at the supports. 1. One end fixed, other end free (no restraints) le = 2. 0 L L

Slenderness Ratio Sr = effective length of column least width of column OK for square section le = b Better to use Sr = effective length of column Least radius of gyration where r= = le r I A I, being the 2 nd Moment of area about C. of G. of cross section A, the cross sectional area

Slenderness Ratio Note for long columns, Ultimate buckling load reduces with increasing slenderness Buckling failure – excess deflection for short columns, Failure due to shear failure Buckling load << shear failure load

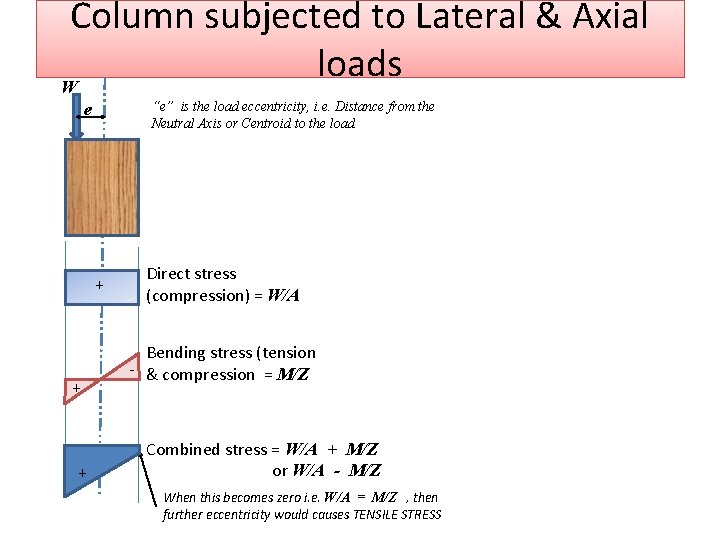
Column subjected to Lateral & Axial loads • Direct or axial load causes direct stress, of same intensity fd = right across section W • Bending stress causes stress to f = b vary across section M • Non axial load causes a combination of the two. (eccentric load) A Z

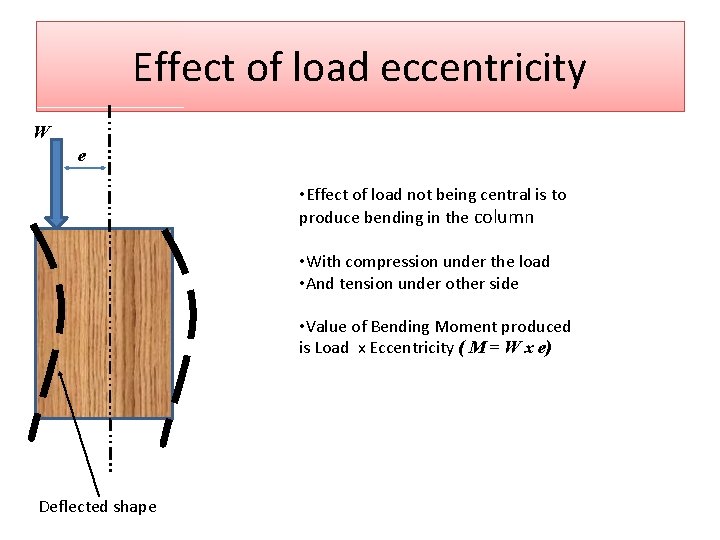
Effect of load eccentricity W e • Effect of load not being central is to produce bending in the column • With compression under the load • And tension under other side • Value of Bending Moment produced is Load x Eccentricity ( M = W x e) Deflected shape

Column subjected to Lateral & Axial loads W “e” is the load eccentricity, i. e. Distance from the Neutral Axis or Centroid to the load e + + + Direct stress (compression) = W/A Bending stress (tension - & compression = M/Z Combined stress = W/A + M/Z or W/A - M/Z When this becomes zero i. e. W/A = M/Z , then further eccentricity would causes TENSILE STRESS

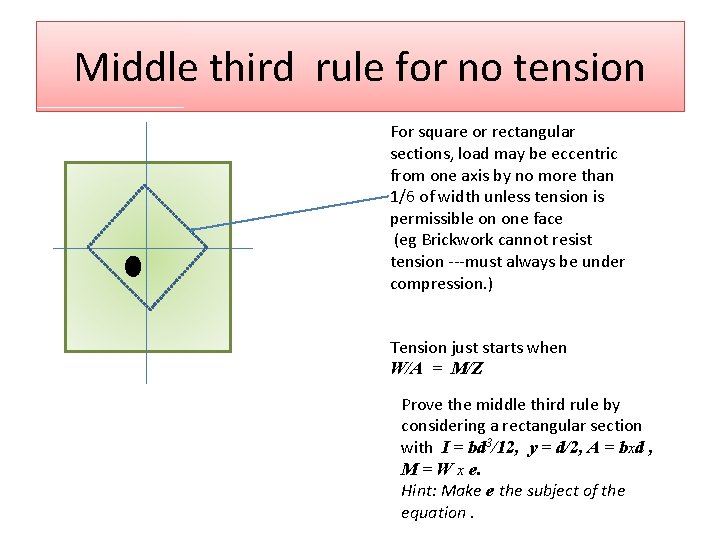
Middle third rule for no tension For square or rectangular sections, load may be eccentric from one axis by no more than 1/6 of width unless tension is permissible on one face (eg Brickwork cannot resist tension ---must always be under compression. ) Tension just starts when W/A = M/Z Prove the middle third rule by considering a rectangular section with I = bd 3/12, y = d/2, A = bxd , M = W x e. Hint: Make e the subject of the equation.

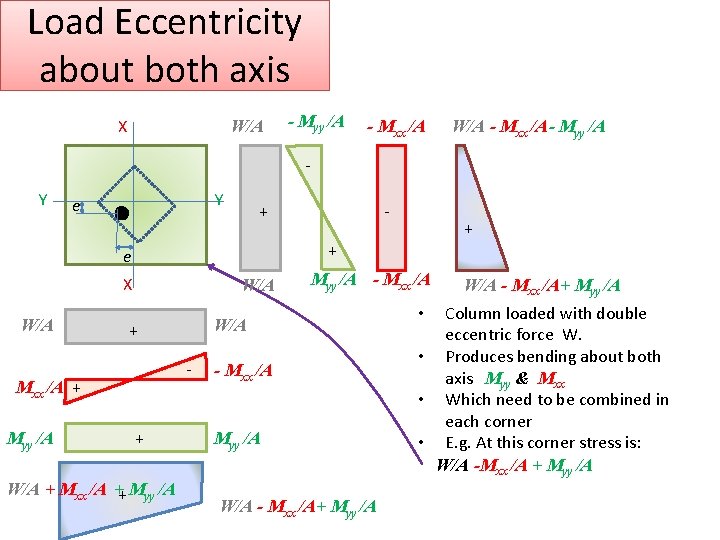
Load Eccentricity about both axis X W/A - Myy /A - Mxx /A W/A - Mxx /A- Myy /A Y Y e + X W/A - + W/A + Mxx /A ++ Myy /A - Mxx /A W/A + Mxx /A + Myy /A + + e W/A - - Mxx /A Myy /A W/A - Mxx /A+ Myy /A Column loaded with double eccentric force W. • Produces bending about both axis Myy & Mxx • Which need to be combined in each corner • E. g. At this corner stress is: W/A -Mxx /A + Myy /A •

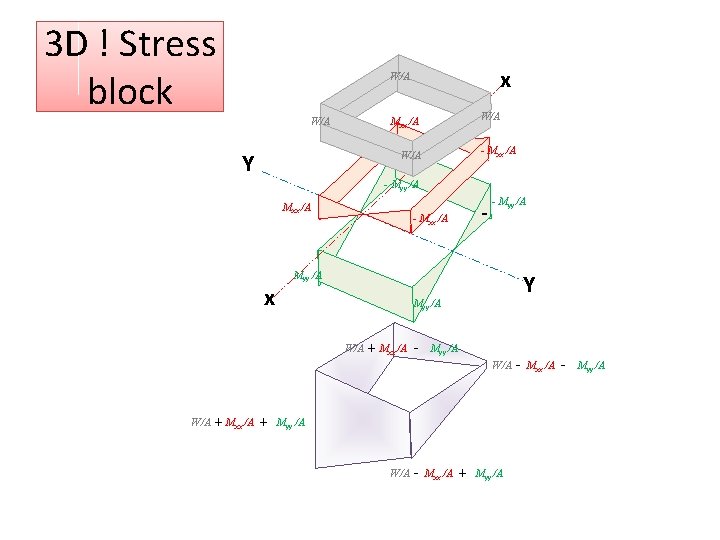
3 D ! Stress block x W/A Mxx /A + Y + x + Myy /A + W/A - Mxx /A W/A - - Myy /A Mxx /A W/A - - Mxx /A - Myy /A Y + Myy /A + Mxx /A - Myy /A W/A + Mxx /A + Myy /A W/A - Mxx /A + Myy /A - Mxx /A - Myy /A