AVL Trees UNIT4Syllabus Symbol Table Representation of Symbol

AVL Trees

UNIT-4(Syllabus) Symbol Table Representation of Symbol Tables- Static tree table and Dynamic tree table, Introduction to Dynamic Programming, Weight balanced tree, Optimal Binary Search Tree (OBST), OBST as an example of Dynamic Programming, Height Balanced Tree- AVL tree.
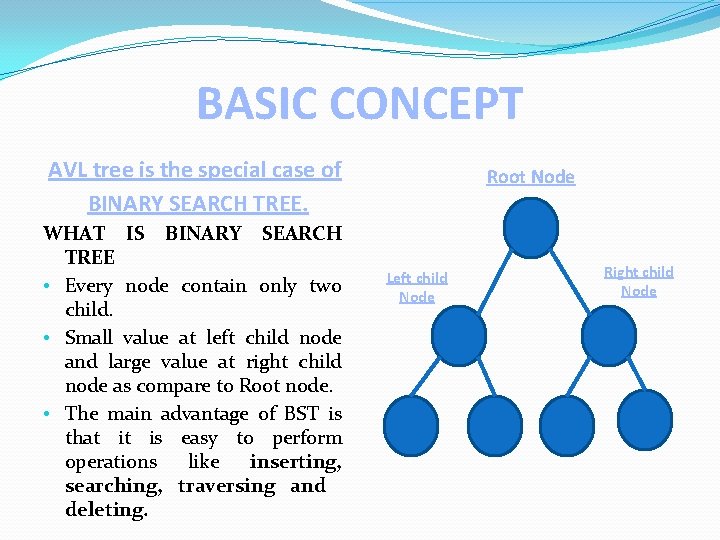
BASIC CONCEPT AVL tree is the special case of BINARY SEARCH TREE. WHAT IS BINARY SEARCH TREE • Every node contain only two child. • Small value at left child node and large value at right child node as compare to Root node. • The main advantage of BST is that it is easy to perform operations like inserting, searching, traversing and deleting. Root Node Left child Node Right child Node
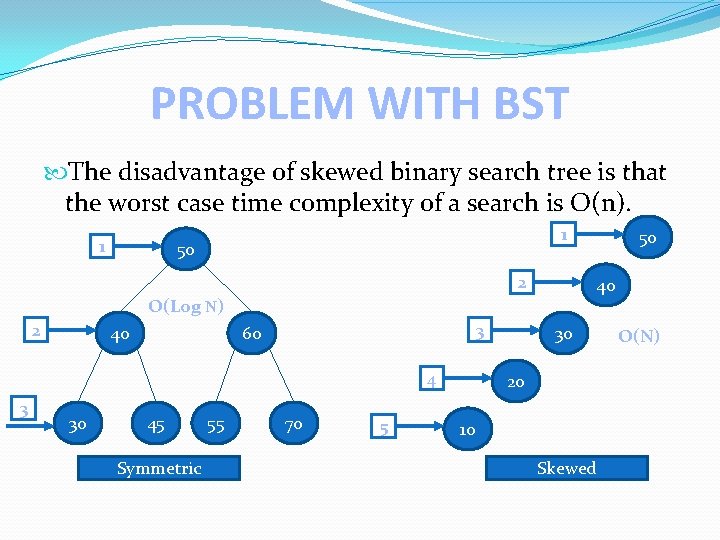
PROBLEM WITH BST The disadvantage of skewed binary search tree is that the worst case time complexity of a search is O(n). 1 1 50 2 40 O(Log N) 2 40 3 60 4 3 30 45 Symmetric 55 70 5 50 30 20 10 Skewed O(N)

NEED TO RESOLVE PROBLEM There is a need to maintain the binary search tree to be of the balanced height, so that it is possible to obtained for the search option a time complexity of O(log N) in the worst case. One of the most popular balanced tree was introduced by Andelson-Velskii and Landis(AVL)

DEFINITION OF AVL TREE A binary tree is said to be an AVL tree if T is a root of tree and T(L) is its left sub tree and T(R) is its right sub-tree of tree T and H(T(L)) and H(T(R)) are the heights of the left and T right sub-trees of T respectively, and |H(T(L)) - H(T(R))|<= 1 Then we called T is AVL tree. -1 0 1 T(L) (R)) H(T Height of left sub-tree minus height of Right left sub-tree [H(T(L)) - H(T(R))] Note: An empty binary tree is an AVL Tree Balance Factor should be H(T (L)) Balance factor T(R)
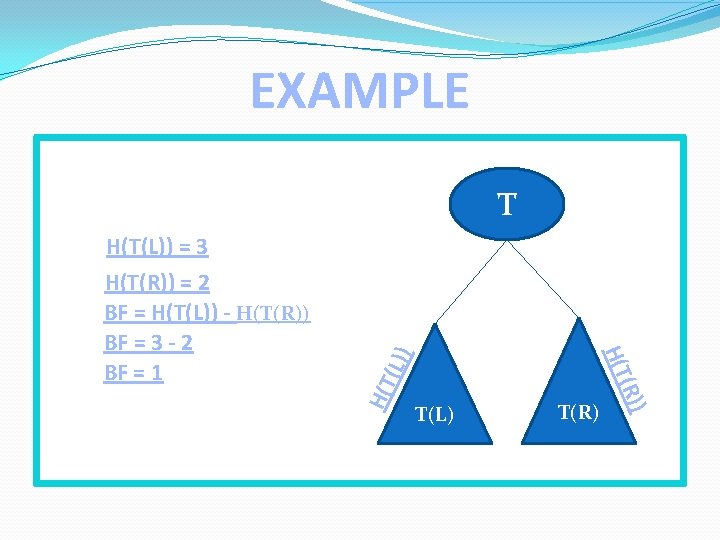
EXAMPLE T(L) (R)) H(T(L)) = 3 H(T(R)) = 2 BF = H(T(L)) - H(T(R)) BF = 3 - 2 BF = 1 H(T (L)) T T(R)

EXAMPLE BF = H(T(L)) - H(T(R)) 50 40 30 2 -0 = 2 1 -0 = 1 0 -0 = 0 UNBALANCE TREE

ROTATION If after the insertion of the element the, the balance factor of any node is affect this problem is over come by using rotation. Rotation is use to restore the balance of search tree.

ROTATION To perform the rotation it is necessary to identify a specific node A whose balance factor (BF) is neither 0, -1 0 r 1 and which is the nearest ancestor to the inserted node on the path from the inserted node to the root. A 40 30 50 2 -0 = 2 1 -0 = 1 0 -0 = 0 Inserted Node

TYPES OF ROTATION LL(Left) rotation. RR(Right) rotation. Single Rotation RL(Right Left) rotation. LR( Left Right) rotation Double Rotation

SINGLE ROTATION Single rotation switches the roles of the parent and child while maintaining the search order. We rotate a node and its child, child becomes parent Parent becomes Right child in LL Rotation. Parent becomes Left child in RR Rotation.
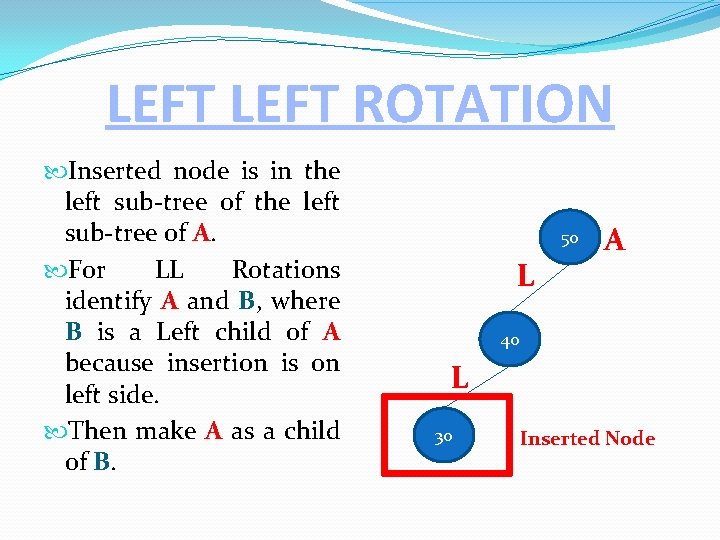
LEFT ROTATION Inserted node is in the left sub-tree of A. For LL Rotations identify A and B, where B is a Left child of A because insertion is on left side. Then make A as a child of B. 50 L A 40 L 30 Inserted Node
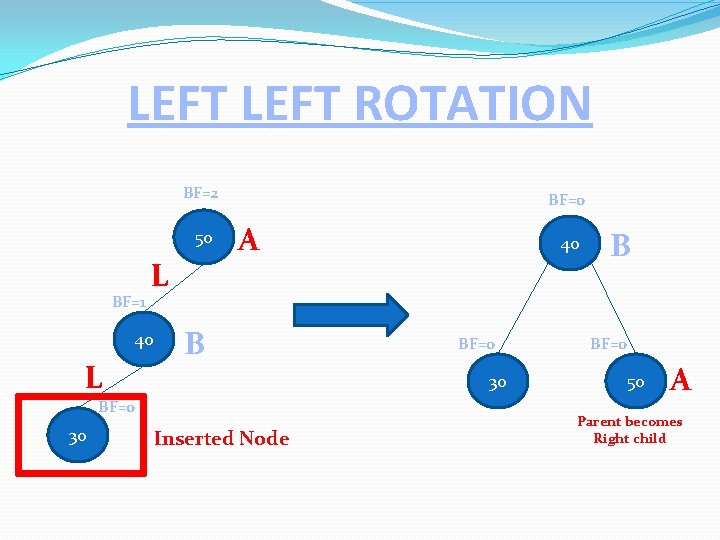
LEFT ROTATION BF=2 50 BF=1 L 40 L BF=0 A B BF=0 30 40 Inserted Node B BF=0 50 A Parent becomes Right child
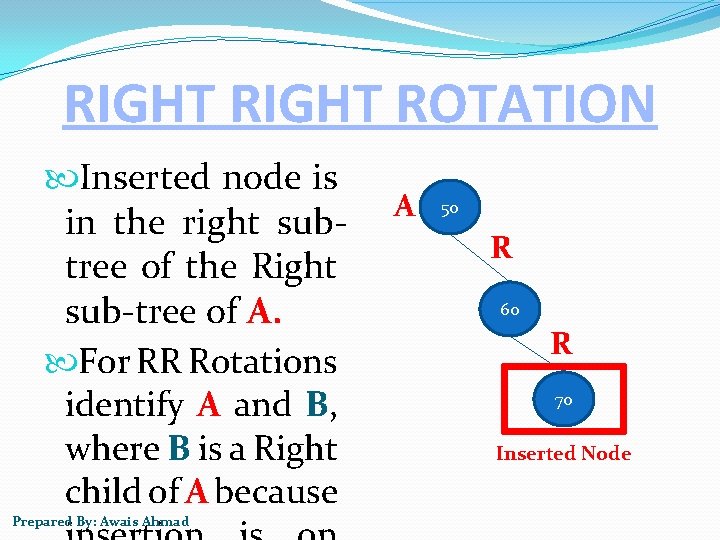
RIGHT ROTATION Inserted node is in the right subtree of the Right sub-tree of A. For RR Rotations identify A and B, where B is a Right child of A because Prepared By: Awais Ahmad A 50 R 60 R 70 Inserted Node
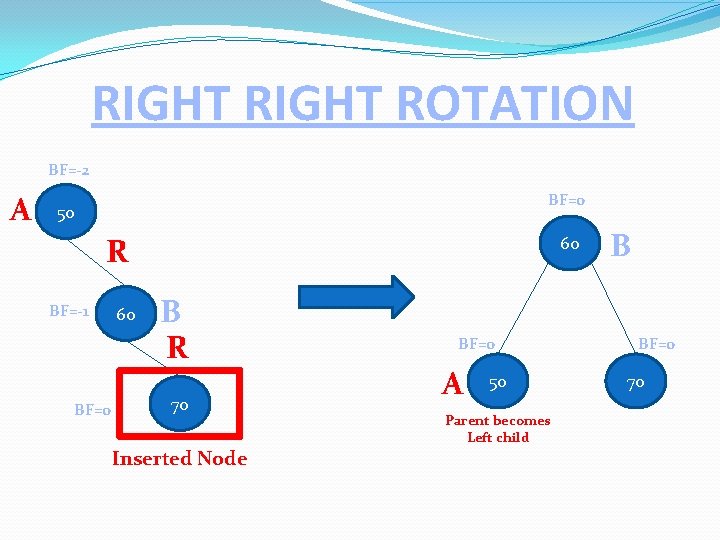
RIGHT ROTATION BF=-2 A BF=0 50 R BF=-1 BF=0 60 60 B R 70 Inserted Node BF=0 A 50 Parent becomes Left child B BF=0 70

DOUBLE ROTATION Single rotation does not fix the LR rotation and RL rotation. LR and RL rotations require a double rotation, involving three node. Double rotation is equivalent to a sequence of two single rotation. 1 st rotation on original tree 2 nd rotation on the new tree
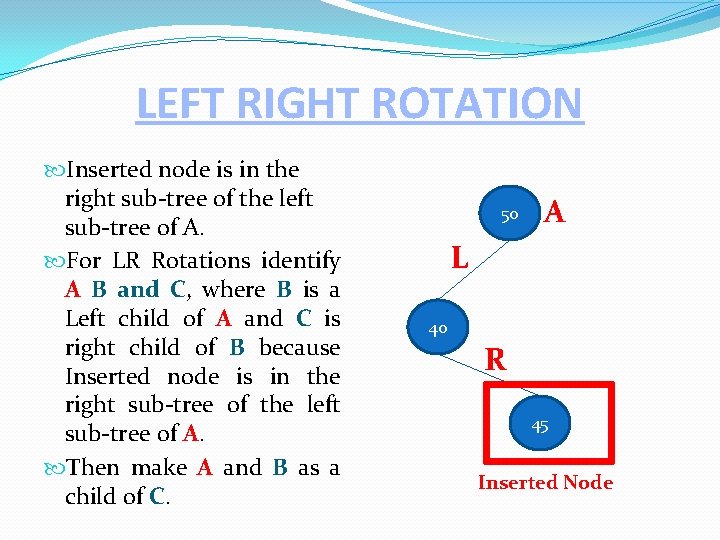
LEFT RIGHT ROTATION Inserted node is in the right sub-tree of the left sub-tree of A. For LR Rotations identify A B and C, where B is a Left child of A and C is right child of B because Inserted node is in the right sub-tree of the left sub-tree of A. Then make A and B as a child of C. 50 A L 40 R 45 Inserted Node
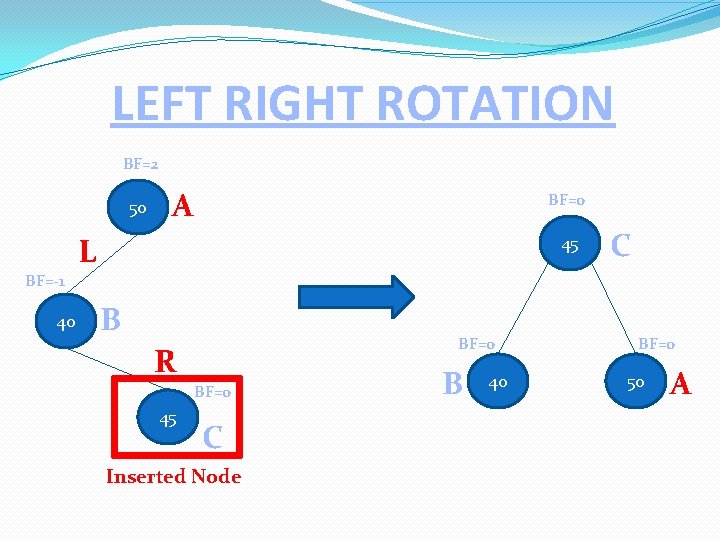
LEFT RIGHT ROTATION BF=2 50 A BF=0 L 45 C BF=-1 40 B BF=0 R BF=0 45 C Inserted Node B 40 BF=0 50 A
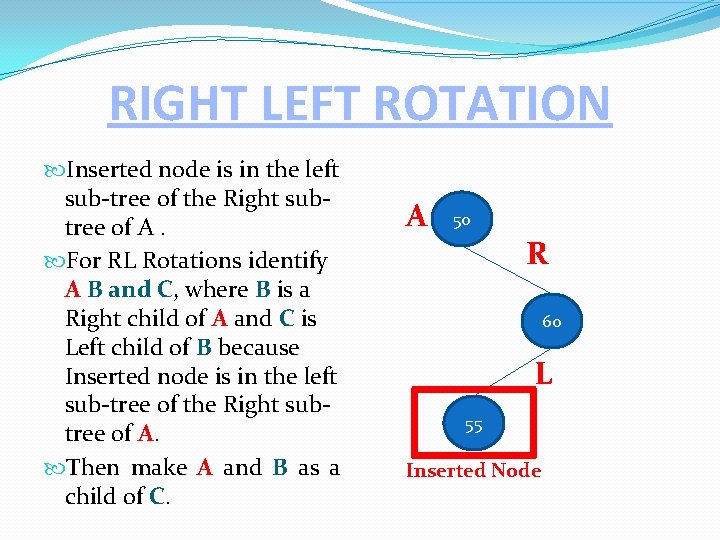
RIGHT LEFT ROTATION Inserted node is in the left sub-tree of the Right subtree of A. For RL Rotations identify A B and C, where B is a Right child of A and C is Left child of B because Inserted node is in the left sub-tree of the Right subtree of A. Then make A and B as a child of C. A 50 R 60 L 55 Inserted Node
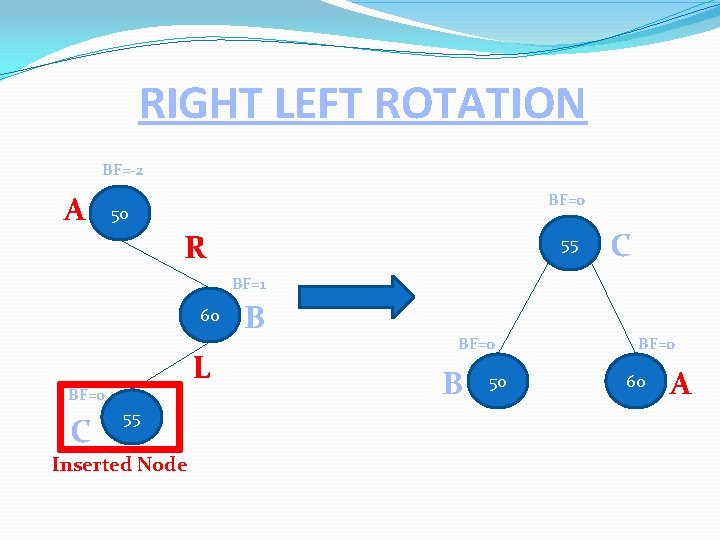
RIGHT LEFT ROTATION BF=-2 A BF=0 50 R 55 C BF=1 60 L BF=0 C 55 Inserted Node B BF=0 B 50 BF=0 60 A

INSERTION // If this node becomes unbalanced, then there are 4 cases // Left Case if (balance > 1 && key < node->left->key) return right. Rotate(node); // Right Case if (balance < -1 && key > node->right->key) return left. Rotate(node);

GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23

GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=0 5

GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 5 BF=0 7

GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 5 BF=-1 7 BF=0 19
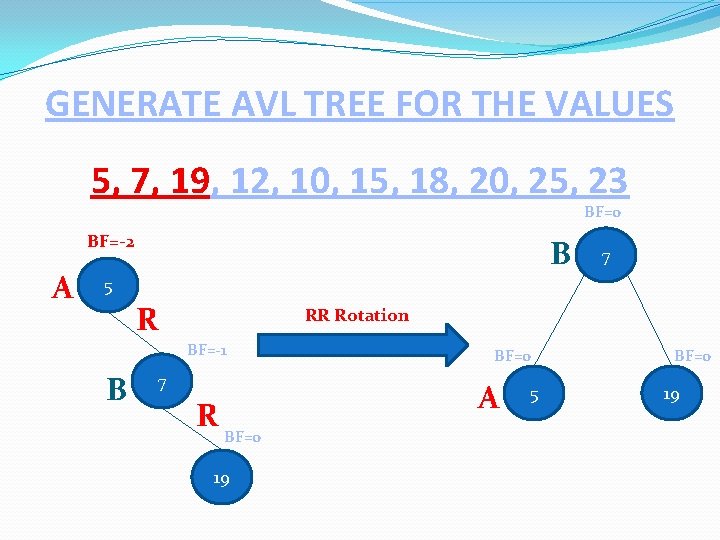
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=0 BF=-2 A B 7 5 R RR Rotation BF=-1 B 7 R BF=0 A BF=0 19 5 BF=0 19
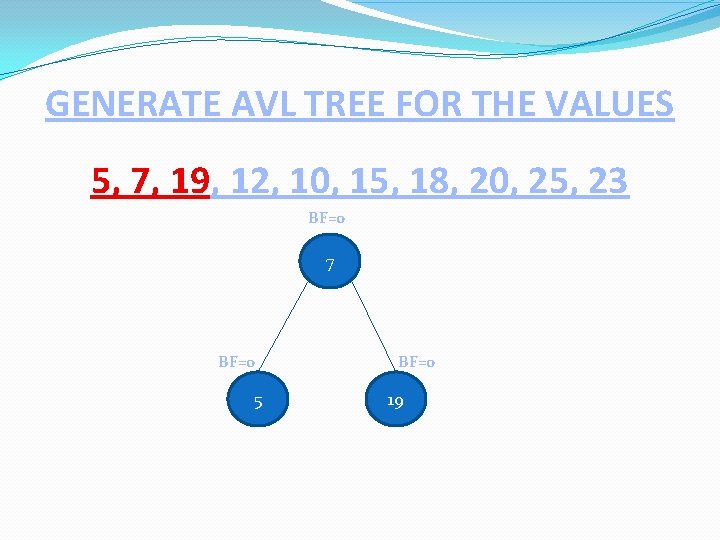
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=0 7 BF=0 5 BF=0 19

GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 7 BF=1 BF=0 H(T(L)) = 1 H(T(R)) = 2 BF = H(T(L)) - H(T(R)) BF = 1 - 2 BF = -1 5 19 BF=0 12

GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 7 BF=0 5 19 12 10 BF=2 BF=1
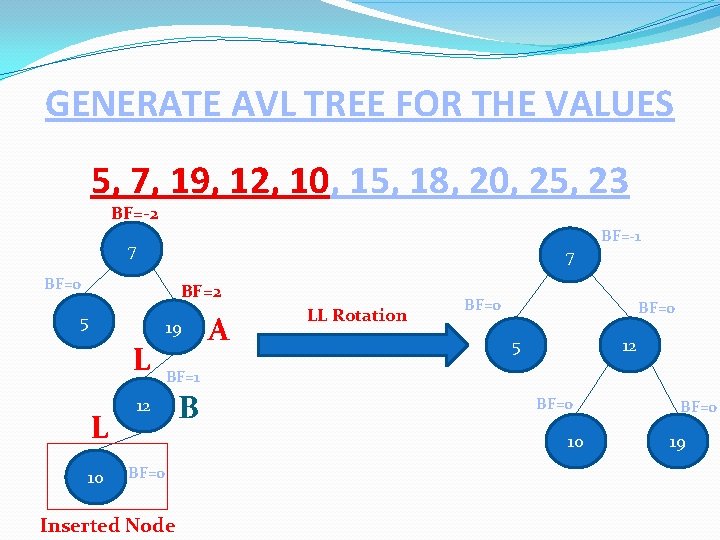
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 7 7 BF=0 BF=2 5 19 L L 10 A LL Rotation BF=-1 BF=0 5 12 BF=1 12 B BF=0 10 BF=0 Inserted Node BF=0 19
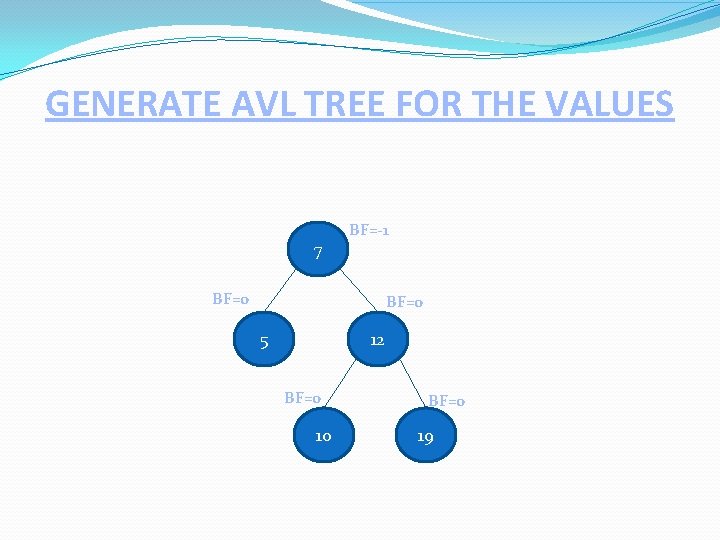
GENERATE AVL TREE FOR THE VALUES 7 BF=-1 BF=0 5 12 BF=0 10 BF=0 19
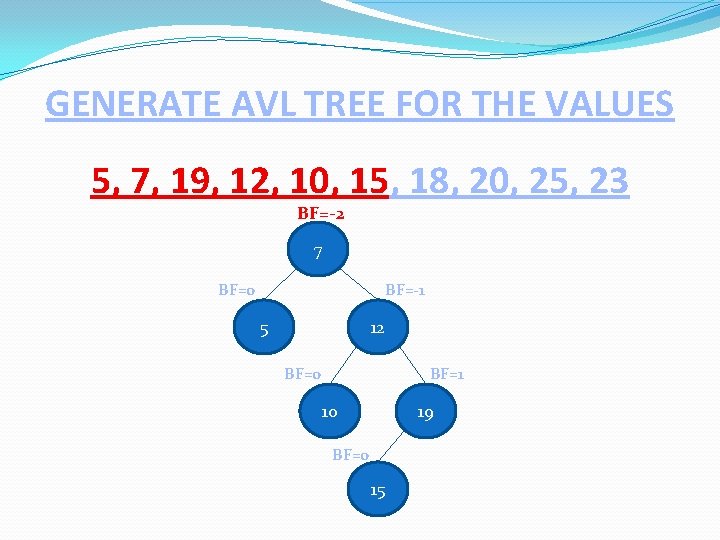
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 7 BF=-1 BF=0 5 12 BF=0 BF=1 10 19 BF=0 15
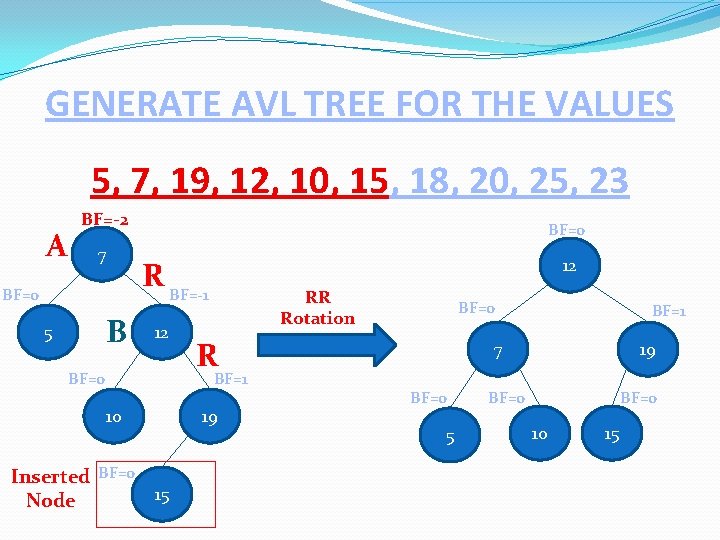
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 A BF=-2 7 B 12 BF=0 RR Rotation 19 BF=0 15 BF=0 R BF=1 10 Inserted Node 12 R BF=-1 BF=0 5 BF=0 BF=1 7 BF=0 5 19 BF=0 10 15
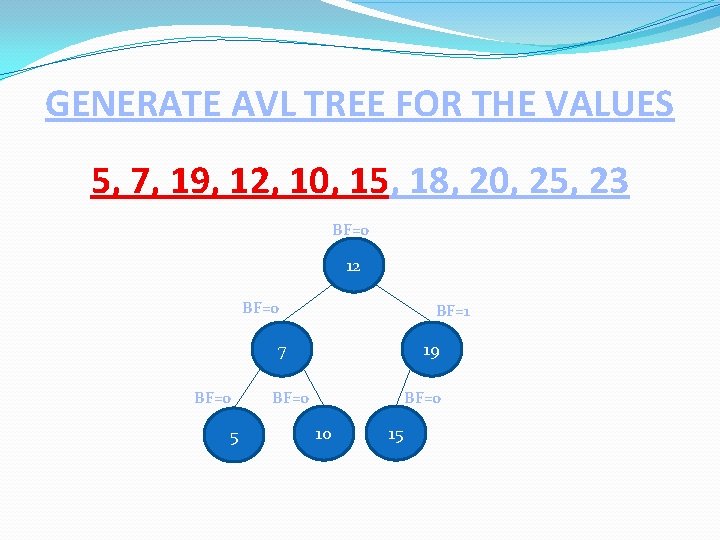
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=0 12 BF=0 BF=1 7 BF=0 5 19 BF=0 10 15
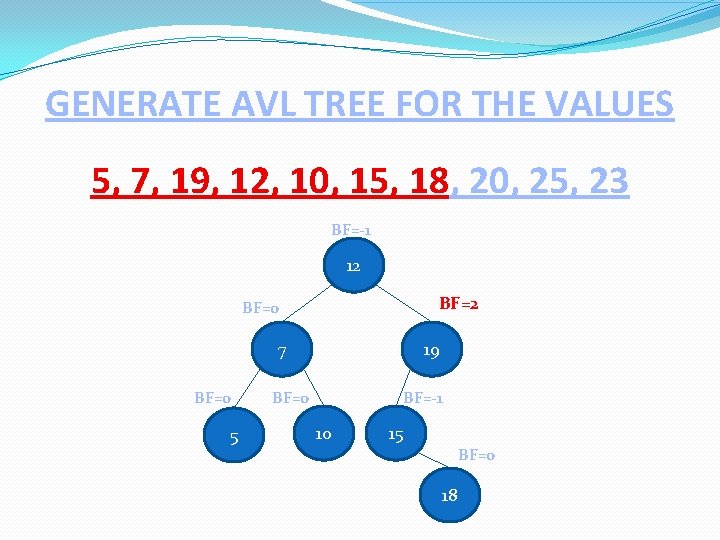
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 12 BF=0 7 BF=0 5 19 BF=-1 BF=0 10 15 BF=0 18
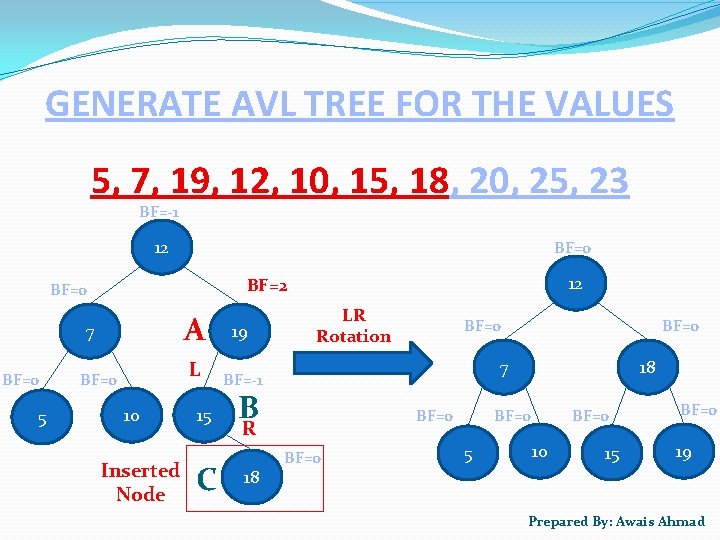
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 12 BF=0 7 BF=0 5 12 BF=0 10 Inserted Node A 19 L BF=-1 15 C LR Rotation BF=0 7 B BF=0 R 18 BF=0 5 BF=0 10 15 BF=0 19 Prepared By: Awais Ahmad
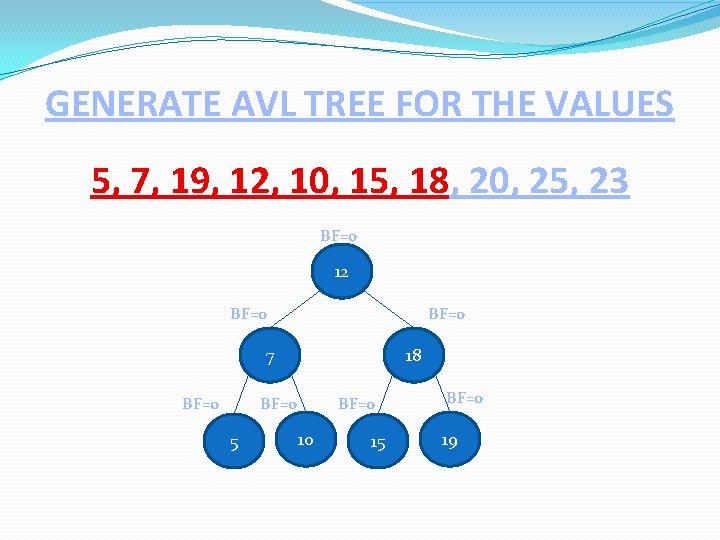
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=0 12 BF=0 7 BF=0 18 BF=0 5 BF=0 10 15 BF=0 19
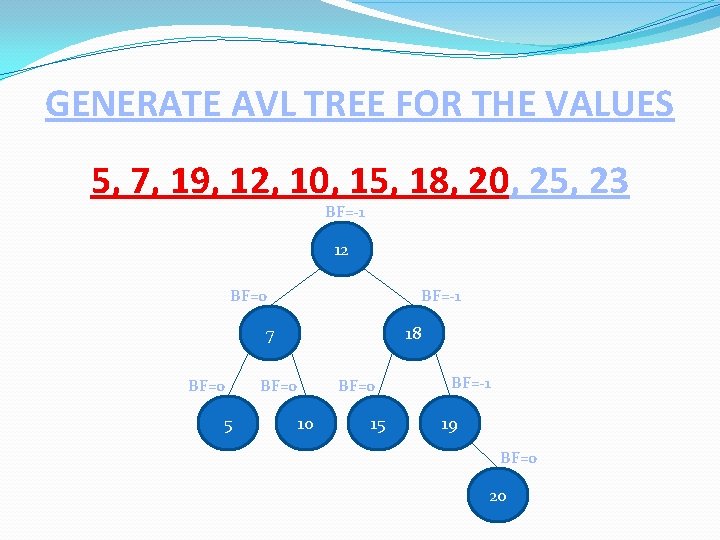
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 12 BF=-1 BF=0 7 BF=0 5 18 BF=0 10 15 BF=-1 19 BF=0 20
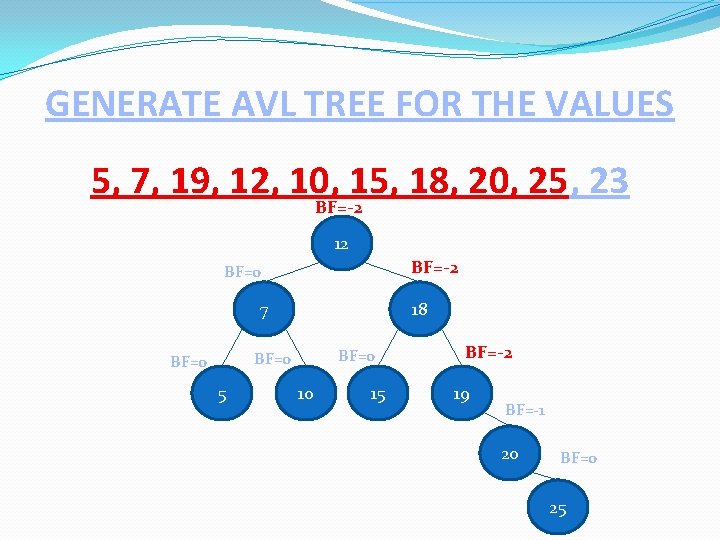
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 12 BF=-2 BF=0 7 18 BF=0 5 10 15 BF=-2 19 BF=-1 20 BF=0 25
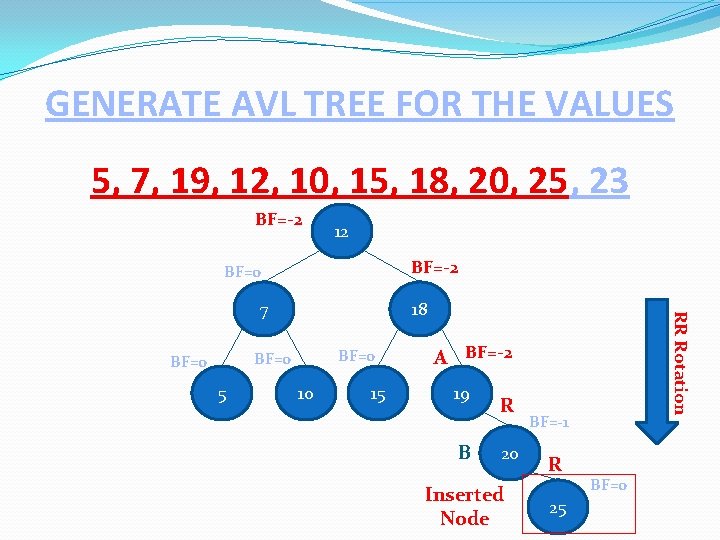
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 12 BF=-2 BF=0 18 BF=0 5 10 15 RR Rotation 7 A BF=-2 19 B R 20 Inserted Node BF=-1 R 25 BF=0
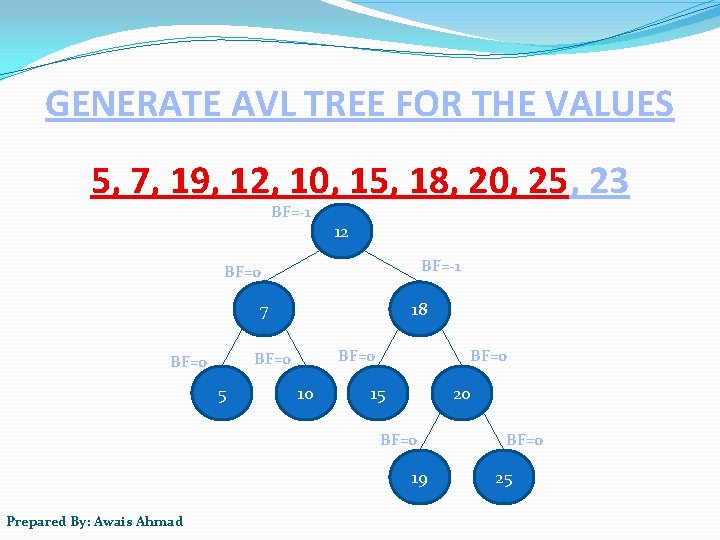
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 12 BF=-1 BF=0 7 18 BF=0 5 10 BF=0 15 20 BF=0 19 Prepared By: Awais Ahmad BF=0 25
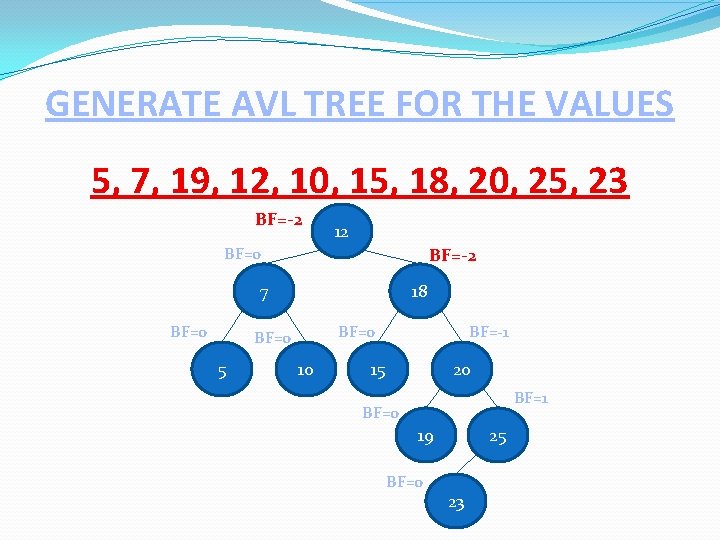
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 12 BF=0 BF=-2 7 BF=0 18 5 BF=-1 BF=0 10 15 20 BF=1 BF=0 19 BF=0 25 23
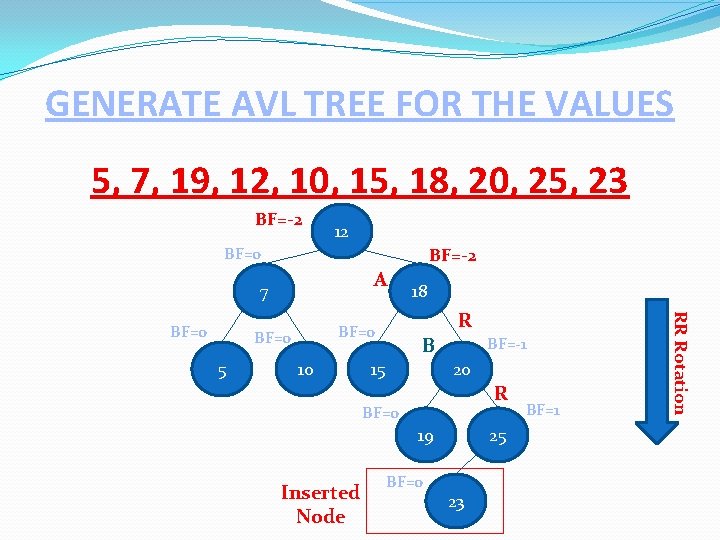
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-2 12 BF=0 BF=-2 A 7 BF=0 5 R BF=0 10 B 15 BF=-1 20 R BF=0 19 Inserted Node BF=0 25 23 BF=1 RR Rotation BF=0 18
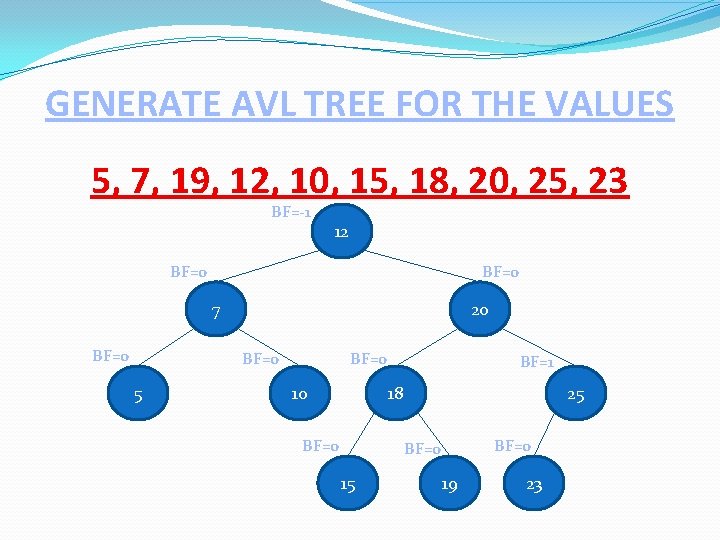
GENERATE AVL TREE FOR THE VALUES 5, 7, 19, 12, 10, 15, 18, 20, 25, 23 BF=-1 12 BF=0 7 BF=0 20 BF=0 5 BF=0 10 BF=1 18 BF=0 25 BF=0 15 19 23
- Slides: 45