AVL trees Today AVL delete and subsequent rotations

AVL trees

Today • AVL delete and subsequent rotations • Testing your knowledge with interactive demos!

AVL tree • Is a binary search tree • Has an additional height constraint: – For each node x in the tree, Height(x. left) differs from Height(x. right) by at most 1 • I promise: – If you satisfy the height constraint, then the height of the tree is O(lg n). – (Proof is easy, but no time! =])

AVL tree • To be an AVL tree, must always: – (1) Be a binary search tree – (2) Satisfy the height constraint • Suppose we start with an AVL tree, then delete as if we’re in a regular BST. • Will the tree be an AVL tree after the delete? – (1) It will still be a BST… – (2) Will it satisfy the height constraint? • (Not covering insert, since you already did in class)

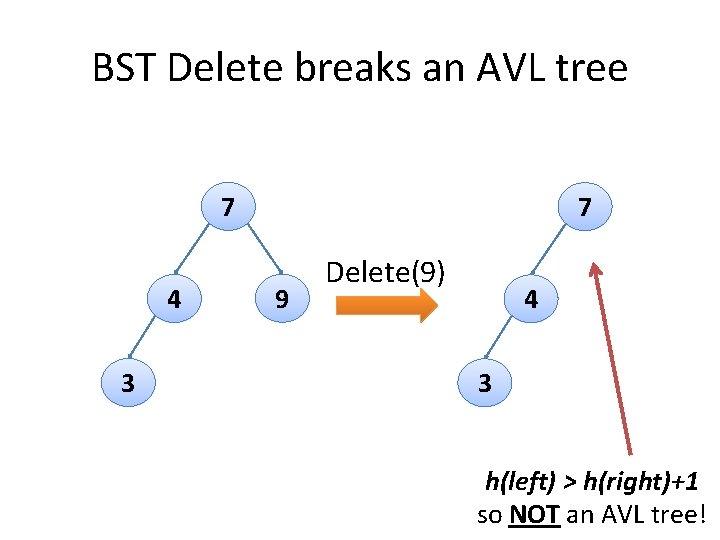
BST Delete breaks an AVL tree 7 4 3 7 9 Delete(9) 4 3 h(left) > h(right)+1 so NOT an AVL tree!

Replacing the height constraint with balance factors • Instead of thinking about the heights of nodes, it is helpful to think in terms of balance factors • The balance factor bf(x) = h(x. right) – h(x. left) – bf(x) values -1, 0, and 1 are allowed – If bf(x) < -1 or bf(x) > 1 then tree is NOT AVL

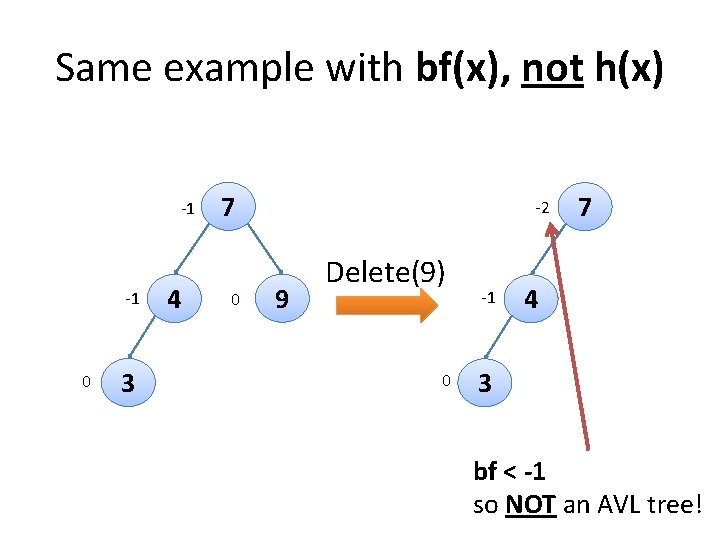
Same example with bf(x), not h(x) -1 -1 0 3 4 7 0 -2 9 Delete(9) 0 -1 7 4 3 bf < -1 so NOT an AVL tree!

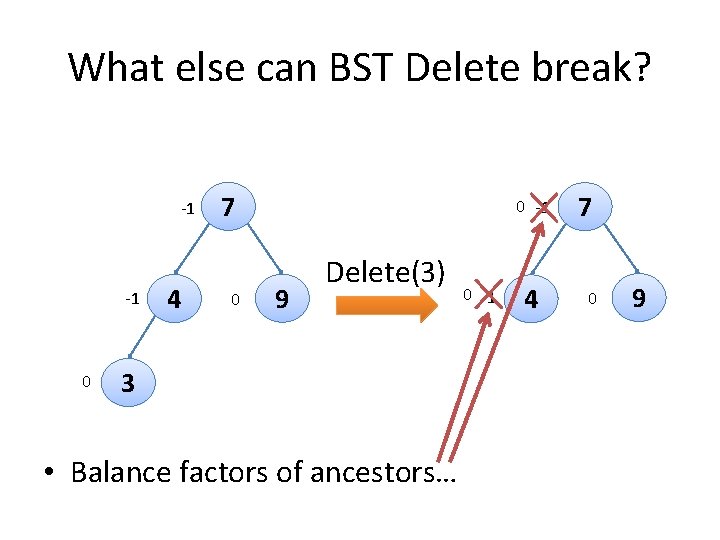
What else can BST Delete break? -1 -1 0 4 7 0 0 -1 9 Delete(3) 3 • Balance factors of ancestors… 0 -1 4 7 0 9

Need a new Delete algorithm • Goal: if tree is AVL before Delete, then tree is AVL after Delete. • Step 1: do BST delete. – This maintains the BST property, but can cause the balance factors of ancestors to be outdated! • Step 2: fix the height constraint and update balance factors. – Update any invalid balance factors affected by delete. – After updating them, they can be < -1 or > 1. – Do rotations to fix any balance factors that are too small or large while maintaining the BST property. – Rotations can cause balance factors to be outdated also!

Bad balance factors • Start with an AVL tree, then do a BST Delete. • What bad values can bf(x) take on? – Delete can reduce a subtree’s height by 1. – So, it might increase or decrease h(x. right) – h(x. left) by 1. – So, bf(x) might increase or decrease by 1. 2 cases – This means: • if bf(x) = 1 before Delete, it might become 2. BAD. • If bf(x) = -1 before Delete, it might become -2. BAD. • If bf(x) = 0 before Delete, then it is still -1, 0 or 1. OK.

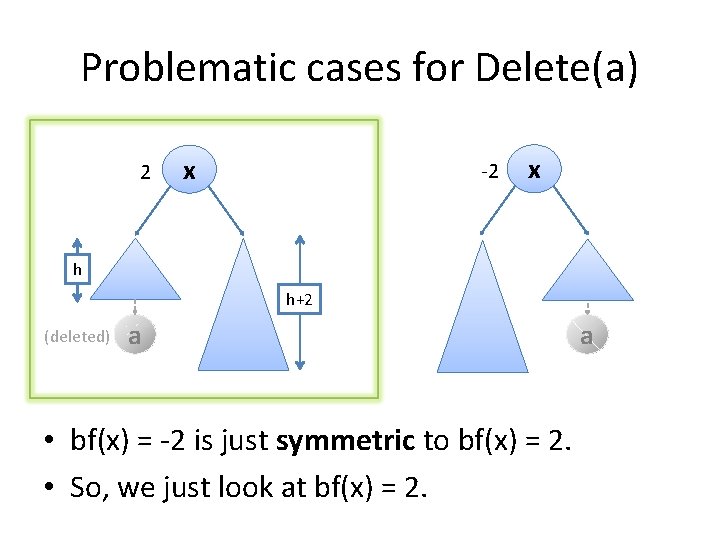
Problematic cases for Delete(a) 2 x -2 x h h+2 (deleted) a • bf(x) = -2 is just symmetric to bf(x) = 2. • So, we just look at bf(x) = 2. a

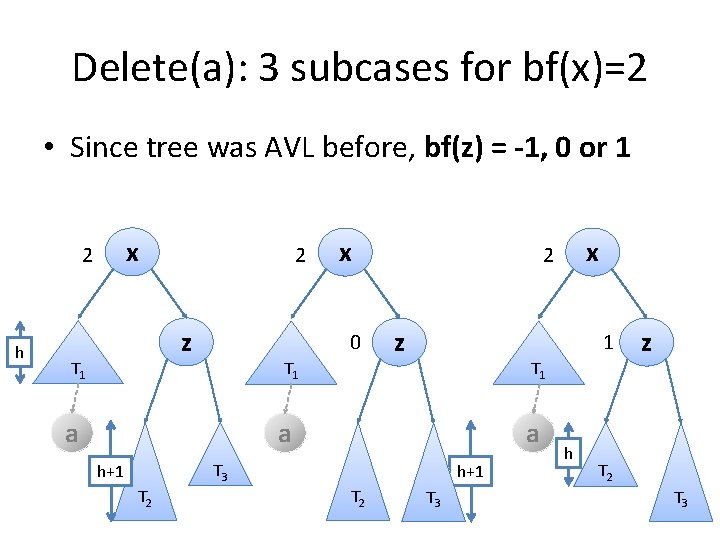
Delete(a): 3 subcases for bf(x)=2 • Since tree was AVL before, bf(z) = -1, 0 or 1 Case bf(z) = -1 Case bf(z) = 0 Case bf(z) = 1 x 2 h -1 T 1 2 z x 0 T 1 a z 1 T 1 a a T 3 h+1 T 2 x 2 T 3 h z T 2 T 3

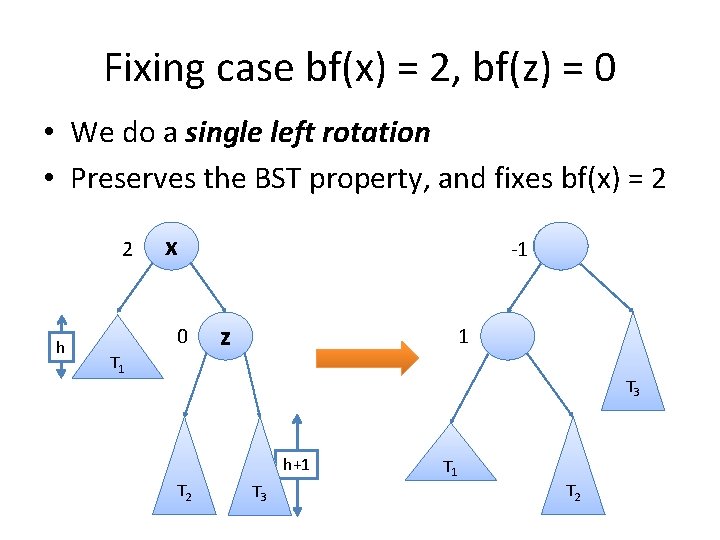
Fixing case bf(x) = 2, bf(z) = 0 • We do a single left rotation • Preserves the BST property, and fixes bf(x) = 2 2 h x 0 T 1 -1 z x T 3 h+1 T 2 T 3 T 1 T 2

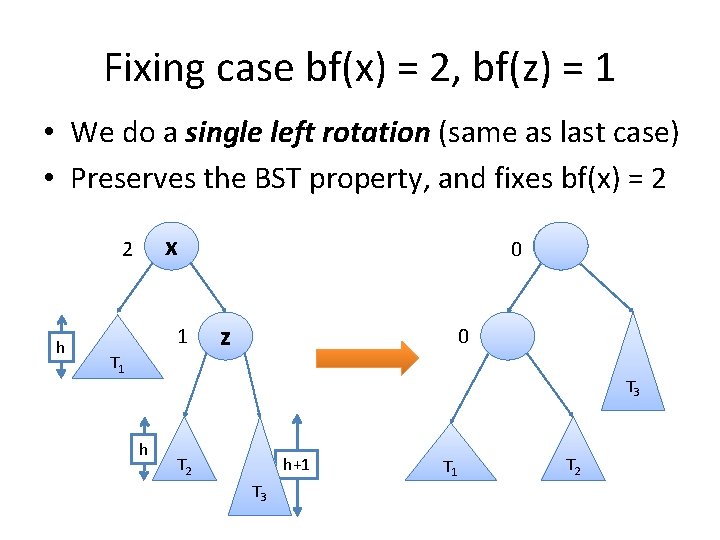
Fixing case bf(x) = 2, bf(z) = 1 • We do a single left rotation (same as last case) • Preserves the BST property, and fixes bf(x) = 2 x 2 h 1 T 1 0 z x T 3 h T 2 h+1 T 3 T 1 T 2

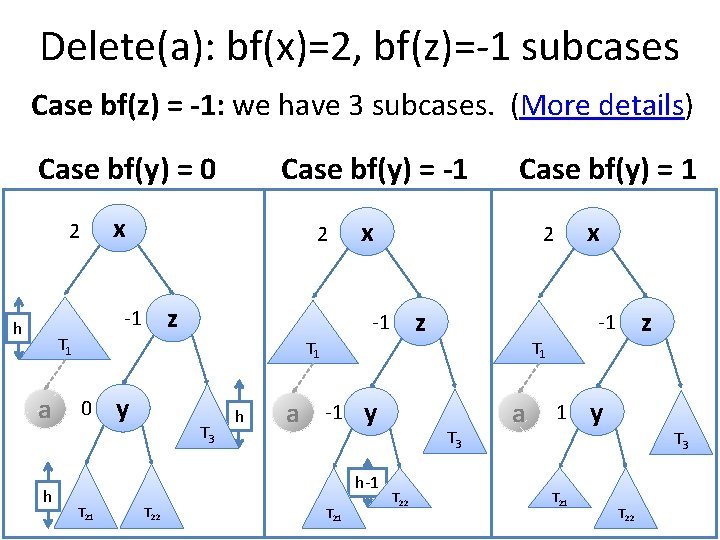
Delete(a): bf(x)=2, bf(z)=-1 subcases Case bf(z) = -1: we have 3 subcases. (More details) Case bf(y) = 0 x 2 2 z -1 h T 1 a h Case bf(y) = -1 x y z -1 T 3 h a -1 y h-1 T 22 T 21 x 2 T 1 0 Case bf(y) = 1 T 3 T 22 z -1 a 1 T 21 y T 3 T 22

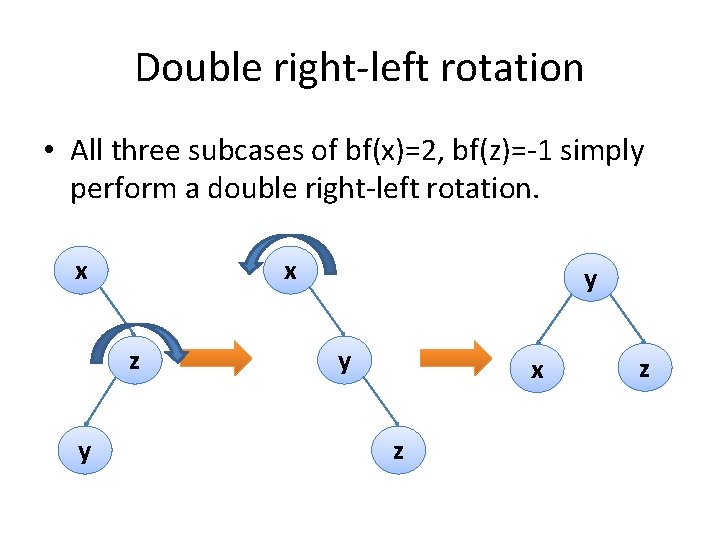
Double right-left rotation • All three subcases of bf(x)=2, bf(z)=-1 simply perform a double right-left rotation. x x z y y y x z z

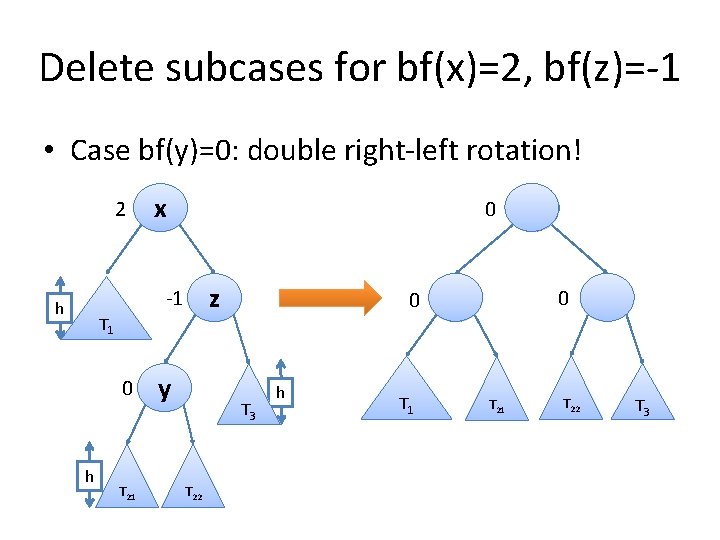
Delete subcases for bf(x)=2, bf(z)=-1 • Case bf(y)=0: double right-left rotation! 2 x 0 z -1 h T 1 0 h T 21 y 0 T 3 T 22 h T 1 x y 0 T 21 T 22 z T 3

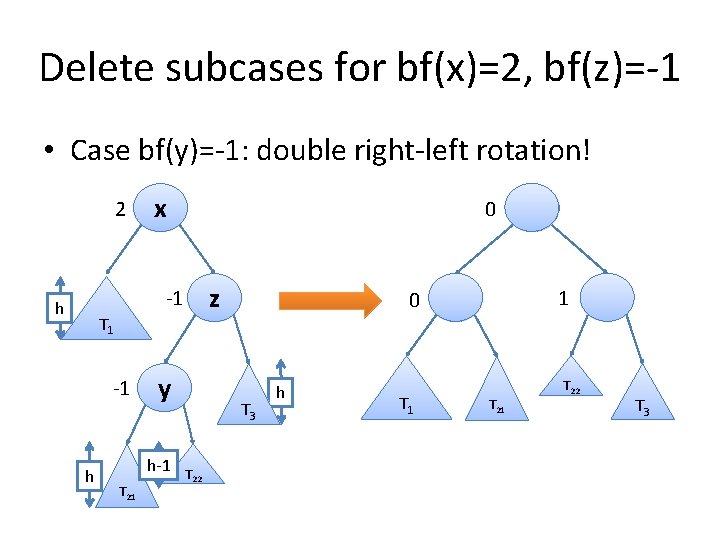
Delete subcases for bf(x)=2, bf(z)=-1 • Case bf(y)=-1: double right-left rotation! 2 x 0 z -1 h T 1 -1 h y h-1 T 21 0 T 3 T 22 h T 1 x y 1 T 22 z T 3

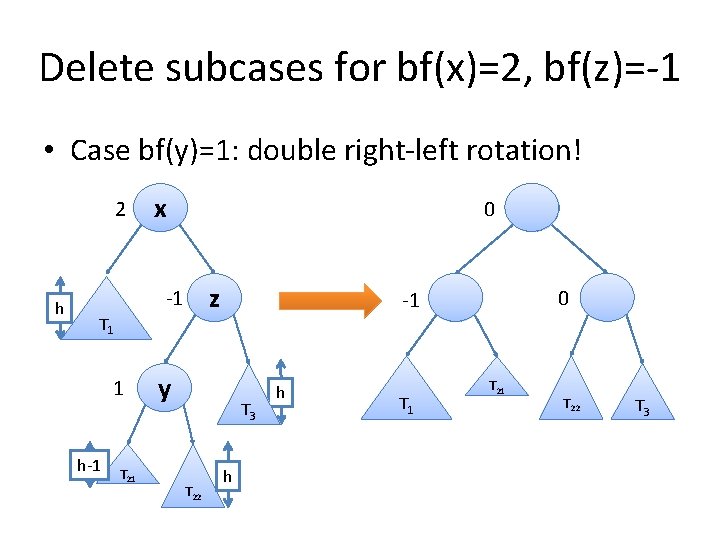
Delete subcases for bf(x)=2, bf(z)=-1 • Case bf(y)=1: double right-left rotation! 2 h x 0 z -1 T 1 1 h-1 T 21 -1 y T 3 T 22 h h T 1 x y 0 T 21 T 22 z T 3

Recursively fixing balance factors • Idea: start at the node we deleted, fix a problem, then recurse up the tree to the root. • At each node x, we update the balance factor: bf(x) : = h(bf. right) - h(bf. left). • If bf(x) = -2 or +2, we perform a rotation. • Then, we update the balance factors of every node that was changed by the rotation. • Finally, we recurse one node higher up.

Interactive AVL Deletes • Interactive web applet