AVL Trees Georgy AdelsonVelsky and Evgenii Landis tree

The AVL tree overview and explanation of its operations were all taken from http:

AVL Tree Overview A self-balancing binary search tree (the first such data structure to

AVL Tree Overview The height of a tree is the number of edges on

Non AVL Tree Height Balanced Tree Midwestern State University images: wikipedia. org

Operations The basic operations of an AVL tree generally involve carrying out the same

Insertion into an AVL tree may be carried out by inserting the given value

Insertion If the balance factor becomes 2 or -2 then the tree rooted at

Insertion Similar to an unbalanced binary search tree, insertion takes O(height) time. This is

Deletion If the node is a leaf, remove it. If the node is not

Deletion The retracing can stop if the balance factor becomes -1 or 1 indicating

Deletion The time required is O(h) for lookup plus O(h) rotations on the way

Lookup in an AVL tree is performed exactly as in an unbalanced binary search

Rotation A tree rotation is an operation on a binary search tree that changes

Rotation Left-Rotate(T, x) x Right-Rotate(T, y) y y Midwestern State University x

Right Rotation Root Q Temp Z M A N Tree. Node *Temp; Temp =

Right Rotation Root Q Temp M N Z A Tree. Node *Temp; Temp =

Right Rotation Root Temp M A Tree. Node *Temp; Temp = Sub. Root->left; Sub.

Right Rotation Root M -1 A Q 0 0 Tree. Node *Temp; N Temp

Left Rotation Root M Temp A Q Tree. Node *Temp; Temp = Sub. Root->right;

Left Rotation Root Temp Q M Z A N Midwestern State University

Left Rotation Root Q M A N Z Midwestern State University

Left Rotation Root Q -1 Z M 0 0 A Tree. Node *Temp; 0

Double Rotations What if we added a node that ended up as one of

Double Rotations Is our tree balanced? ? No so we do a right rotation,

Double Rotations Lets try…. Root Q Temp Z M A N P Midwestern State

Double Rotations Are we balanced? ? Root M A Q Z N P Midwestern

Double Rotations The reason our right rotation did not work, is because the left

Double Rotations To fix the problem, we must do a “left rotation” on the

Double Rotations Do a left rotation on the “right subtree” Root Q Sub. Root

Double Rotations Now our “left” subtree is “left” heavy and we can do a

Double Rotations void Avl. Tree: : Rotate. Left(Tree. Node *&Sub. Root){ if(Left. Heavy(Sub. Root->right)){

An Extended Example Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14

An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16,

An Extended Example Calculate Balance Factor Insert 3, 2, 1, 4, 5, 6, 7,

An Extended Example Calculate Balance Factors Insert 3, 2, 1, 4, 5, 6, 7,

An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16,

An Extended Example Rotate and re-calculate Insert 3, 2, 1, 4, 5, 6, 7,

An Extended Example Insert a value Insert 3, 2, 1, 4, 5, 6, 7,

An Extended Example Rotate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15,

An Extended Example Re-calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16,

An Extended Example Delete 15 // // delete node with 1 child (right) node.

An Extended Example Re-calculate balance factors 4 -1 2 1 0 14 0 3

An Extended Example Delete 14 // delete node with 2 children // replace with

An Extended Example Re-calculate balance factors 4 -1 2 1 0 16 0 -2

An Extended Example Right Rotation necessary 4 Sub. Root -1 Temp = Sub. Root->left;

An Extended Example Right Rotation necessary 4 -1 Temp = Sub. Root->left; Sub. Root->left

An Extended Example Re-calculate balance factors 4 -1 2 1 0 6 0 3

AVL Implementation All methods mimic a BST implementation (with one tiny modification: rotations). The

AVL Implementation Methods that “I” (meaning, not necessarily the best implementation) added to maintain

$Height int BSTree: : Height(Tree. Node *node. Ptr){ int left_height=0; int right_height=0; if(node. Ptr==NULL)$

Avl. Value int BSTree: : Avl. Value(Tree. Node *node. Ptr) { int leftheight =

Left / Right Heavy bool BSTree: : Left. Heavy(Tree. Node * ptr) { return

Rotate Left/Right void BSTree: : Rotate. Left(Tree. Node *& Sub. Root) { if (Sub.

Compute. Avl. Values void BSTree: : Compute. Avl. Values(Tree. Node *&node. Ptr) { if(node.

Slides: 115

Download presentation

AVL Trees (Georgy Adelson-Velsky and Evgenii Landis' tree, named after the inventors) Terry Griffin Computer Science II Midwestern State University

The AVL tree overview and explanation of its operations were all taken from http: //en. wikipedia. org/wiki/AVL_tree Wikipedia’s copyright information can be viewed here: http: //en. wikipedia. org/wiki/Wikipedia: Copyrights Midwestern State University

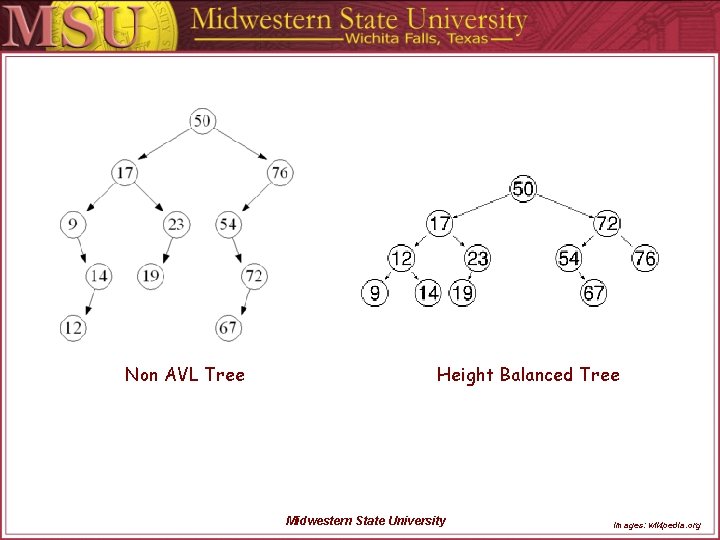
AVL Tree Overview A self-balancing binary search tree (the first such data structure to be invented). The heights of the left and right subtrees differ by no more than 1 level. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases. Additions and deletions may require the tree to be rebalanced by one or more tree rotations. Midwestern State University

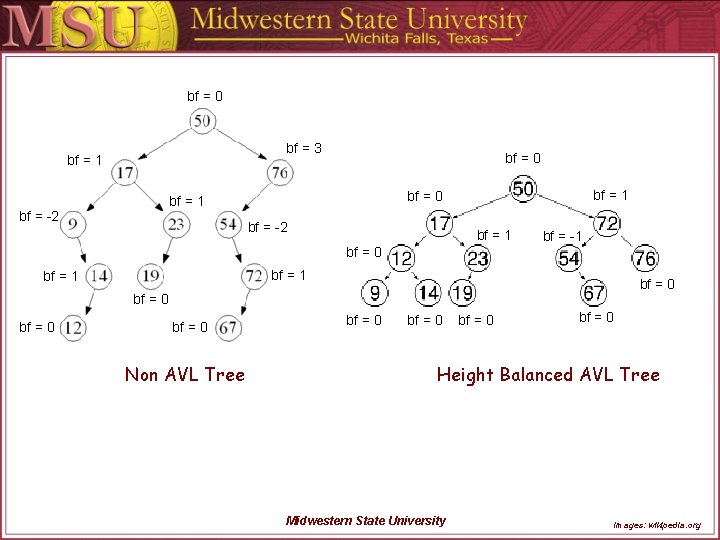
AVL Tree Overview The height of a tree is the number of edges on the longest downward path between the root and a leaf. The balance factor of a node is the height of its left subtree minus the height of its right subtree. A node with balance factor 1, 0, or -1 is considered balanced. A node with any other balance factor is considered unbalanced and requires rebalancing the tree. The balance factor is either stored directly at each node or computed from the heights of the subtrees. Midwestern State University

Non AVL Tree Height Balanced Tree Midwestern State University images: wikipedia. org

bf = 0 bf = 3 bf = 1 bf = 0 bf = -2 bf = 1 bf = 0 bf = 1 bf = -2 bf = 1 bf = -1 bf = 0 bf = 0 Non AVL Tree bf = 0 Height Balanced AVL Tree Midwestern State University images: wikipedia. org

Operations The basic operations of an AVL tree generally involve carrying out the same algorithms as would be carried out on an unbalanced binary search tree. The difference is they are preceded or followed by one or more of the so-called "AVL rotations. " Midwestern State University

Insertion into an AVL tree may be carried out by inserting the given value into the tree as if it were an unbalanced binary search tree, and then retracing one's steps toward the root updating the balance factor of the nodes. Retracing is stopped when a node's balance factor becomes 0, 1, or -1. If the balance factor becomes 0 then the height of the subtree hasn't changed because of the insert. The insertion is finished. Midwestern State University

Insertion If the balance factor becomes 2 or -2 then the tree rooted at this node is unbalanced, and a tree rotation is needed. The tree rotation will always leave the subtree evenly balanced. The rotation can be done in constant time. Midwestern State University

Insertion Similar to an unbalanced binary search tree, insertion takes O(height) time. This is O(height) to find the insertion point plus O(height) to check for any needed rotations. Midwestern State University

Deletion If the node is a leaf, remove it. If the node is not a leaf, replace it with either the largest in its left subtree or the smallest in its right subtree, and remove that node. Thus the node that is removed has at most one child. After deletion retrace the path back up the tree to the root, adjusting the balance factors as needed. Midwestern State University

Deletion The retracing can stop if the balance factor becomes -1 or 1 indicating that the height of that subtree has remained unchanged. If the balance factor becomes 0 then the height of the subtree has decreased by one and the retracing needs to continue. If the balance factor becomes -2 or 2 then the subtree is unbalanced and needs to be rotated to fix it. If the rotation leaves the subtree's balance factor at 0 then the retracing towards the root must continue since the height of this subtree has decreased by one. This is in contrast to an insertion where a rotation resulting in a balance factor of 0 indicated that the subtree's height has remained unchanged. Midwestern State University

Deletion The time required is O(h) for lookup plus O(h) rotations on the way back to the root. So the operation can be completed in O(log n) time. Midwestern State University

Lookup in an AVL tree is performed exactly as in an unbalanced binary search tree. But is guaranteed to takes O(log n) time, since an AVL tree is always kept balanced (this is not guaranteed in a BST). No special provisions need to be taken, and the tree's structure is not modified by lookups. Midwestern State University

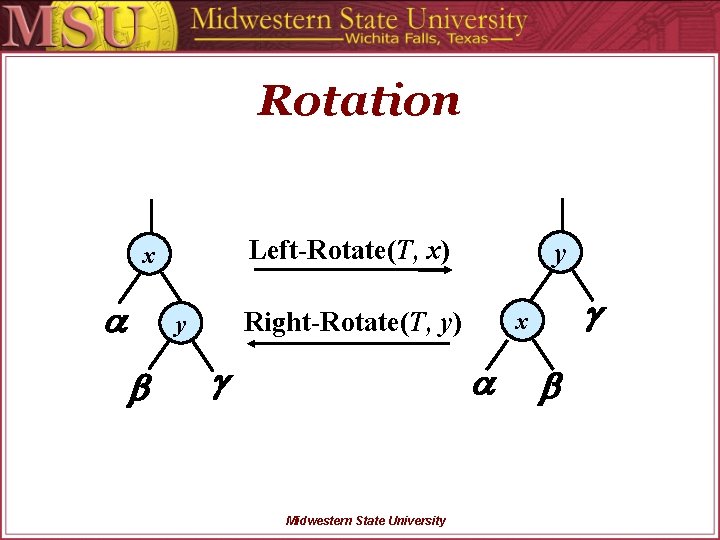
Rotation A tree rotation is an operation on a binary search tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down. They are used to change the shape of the tree, and in particular to decrease its height by moving smaller subtrees down and larger subtrees up, resulting in improved performance of many tree operations. Midwestern State University

Rotation Left-Rotate(T, x) x Right-Rotate(T, y) y y Midwestern State University x

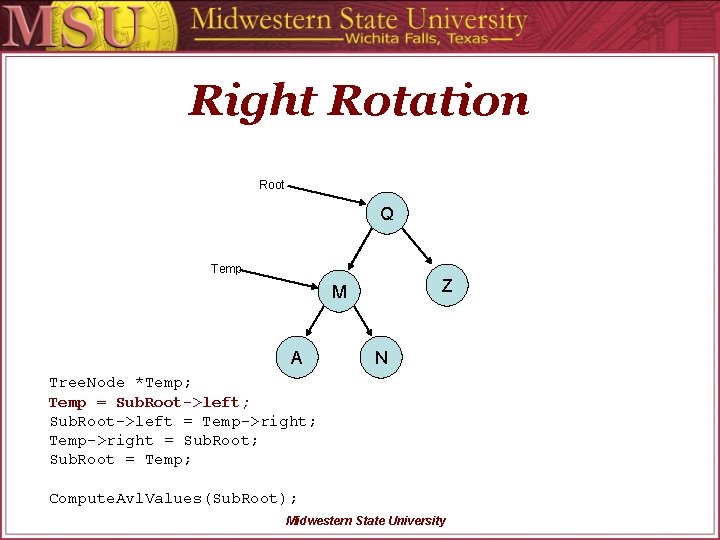
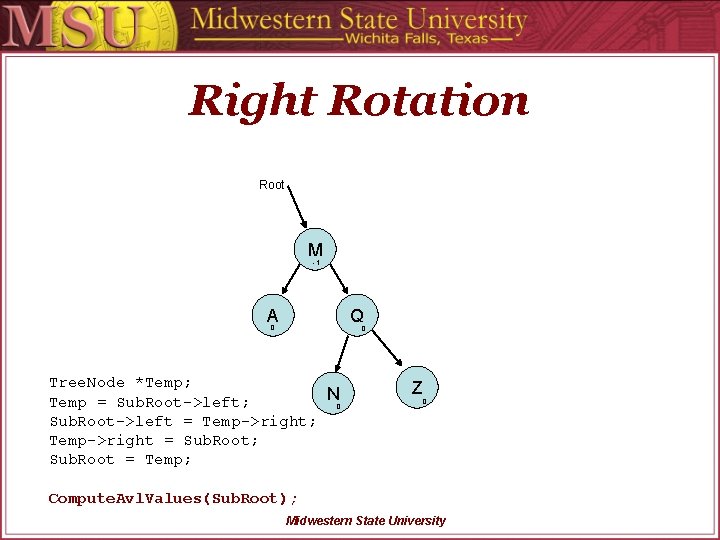
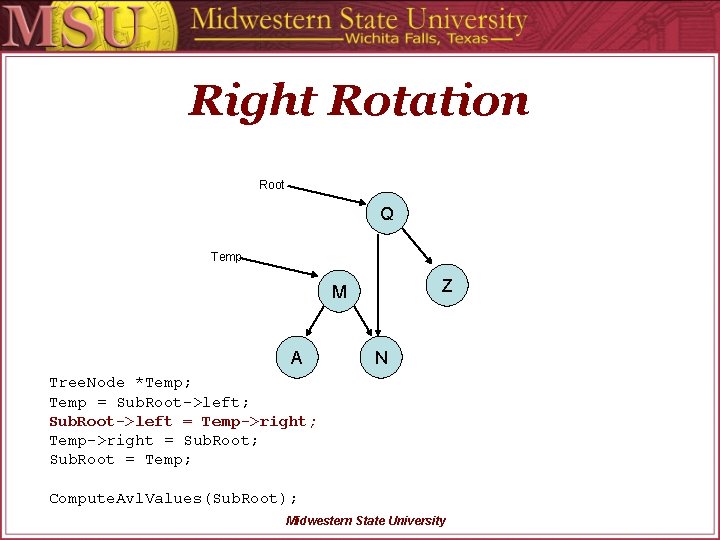
Right Rotation Root Q Temp Z M A N Tree. Node *Temp; Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); Midwestern State University

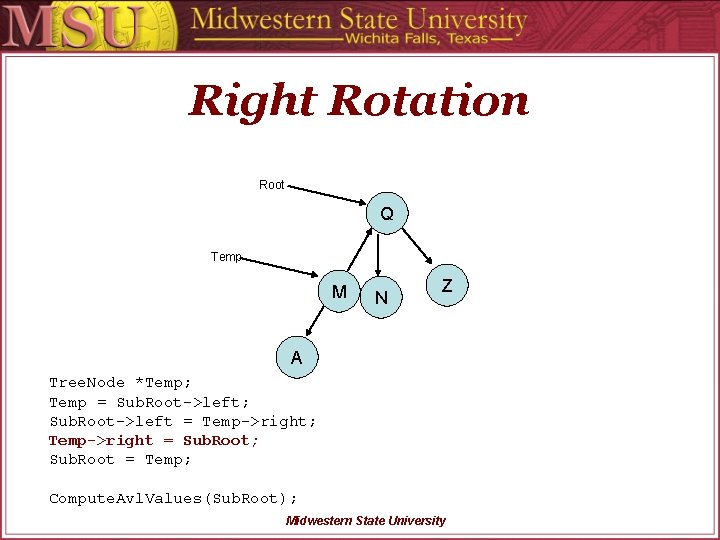
Right Rotation Root Q Temp M N Z A Tree. Node *Temp; Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); Midwestern State University

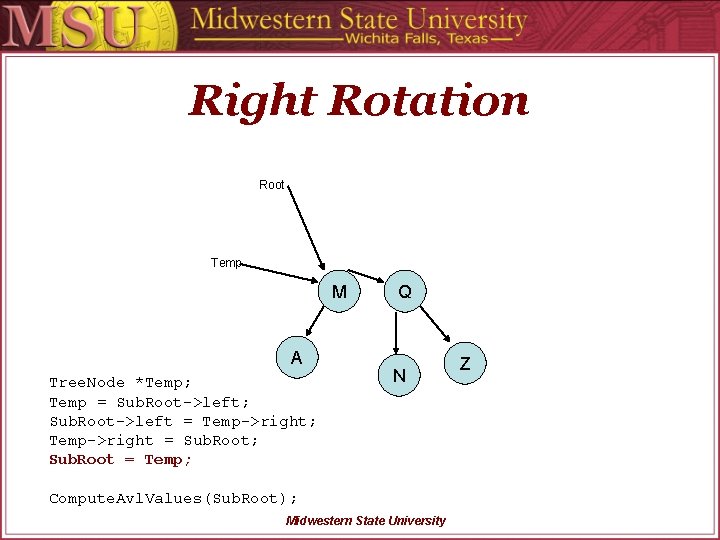
Right Rotation Root Temp M A Tree. Node *Temp; Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Q N Compute. Avl. Values(Sub. Root); Midwestern State University Z

Right Rotation Root M -1 A Q 0 0 Tree. Node *Temp; N Temp = Sub. Root->left; 0 Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Z 0 Compute. Avl. Values(Sub. Root); Midwestern State University

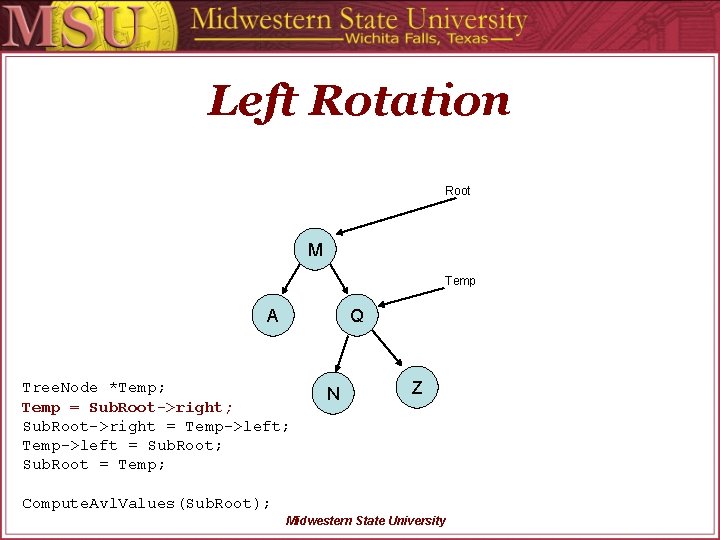
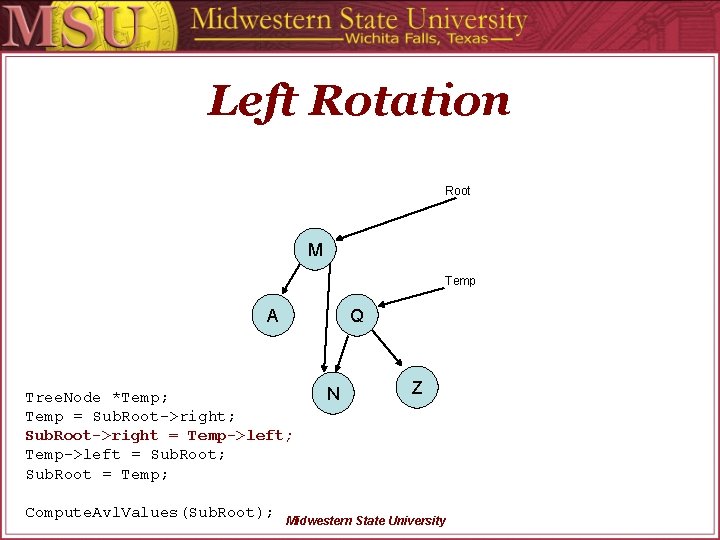
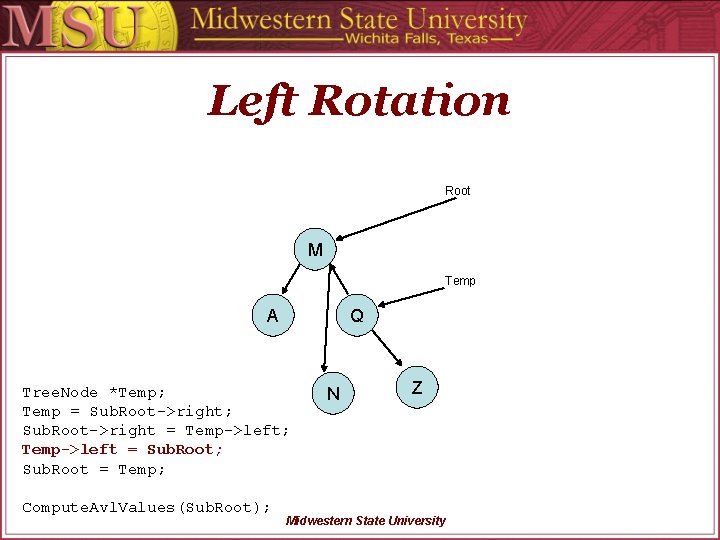
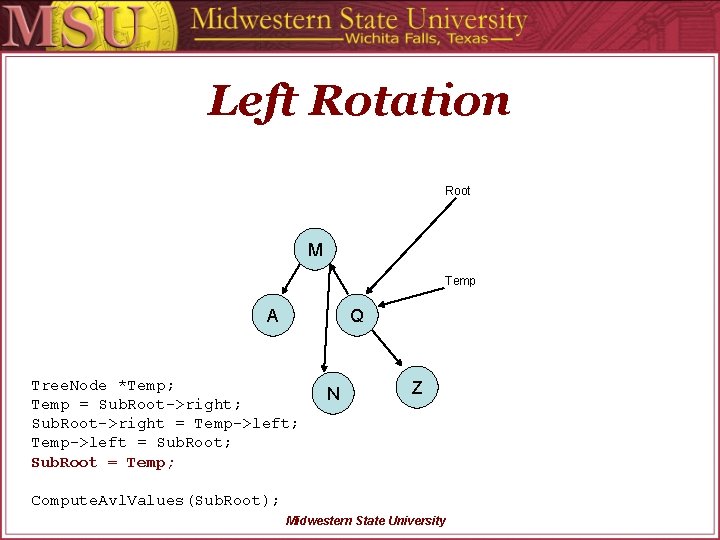
Left Rotation Root M Temp A Q Tree. Node *Temp; Temp = Sub. Root->right; Sub. Root->right = Temp->left; Temp->left = Sub. Root; Sub. Root = Temp; N Z Compute. Avl. Values(Sub. Root); Midwestern State University

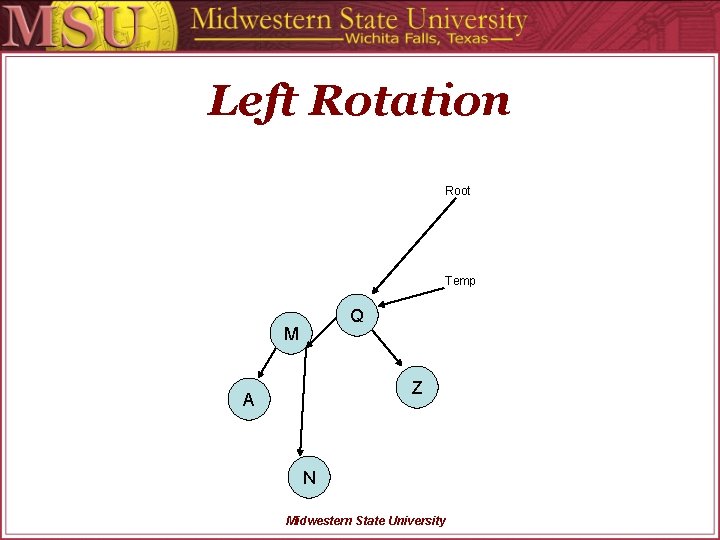
Left Rotation Root M Temp A Q Tree. Node *Temp; Temp = Sub. Root->right; Sub. Root->right = Temp->left; Temp->left = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); N Z Midwestern State University

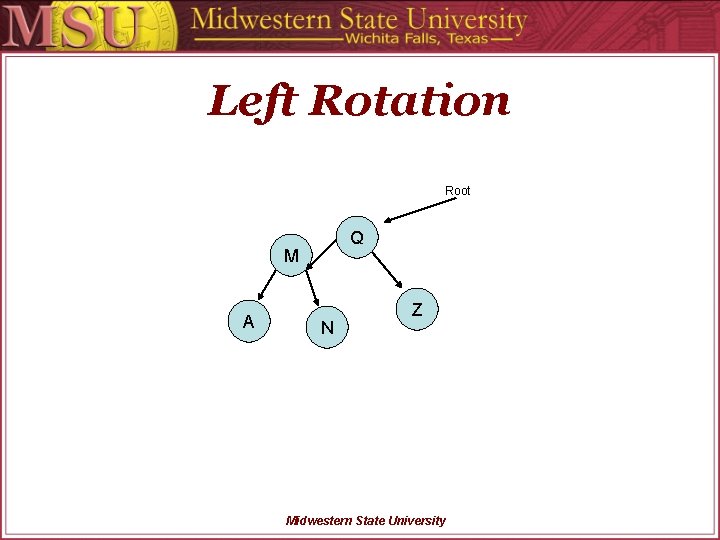
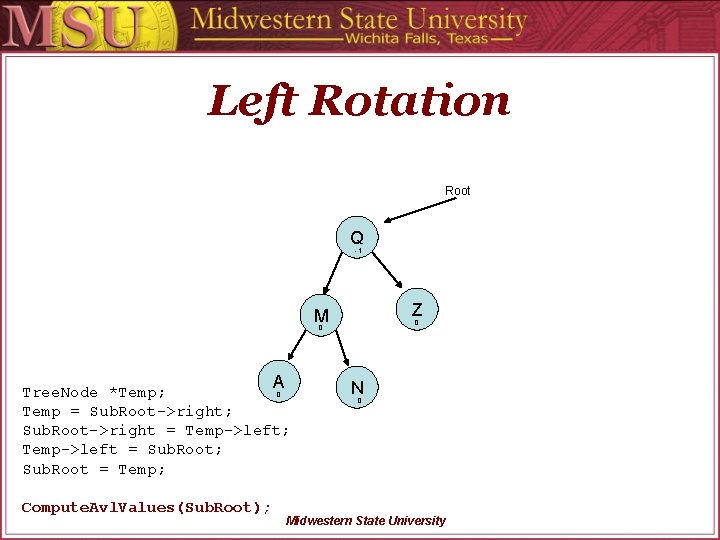
Left Rotation Root Temp Q M Z A N Midwestern State University

Left Rotation Root Q M A N Z Midwestern State University

Left Rotation Root Q -1 Z M 0 0 A Tree. Node *Temp; 0 Temp = Sub. Root->right; Sub. Root->right = Temp->left; Temp->left = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); N 0 Midwestern State University

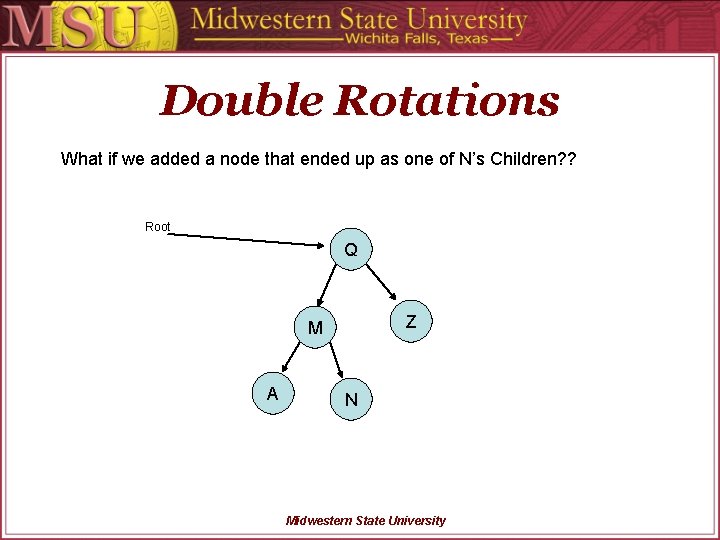
Double Rotations What if we added a node that ended up as one of N’s Children? ? Root Q Z M A N Midwestern State University

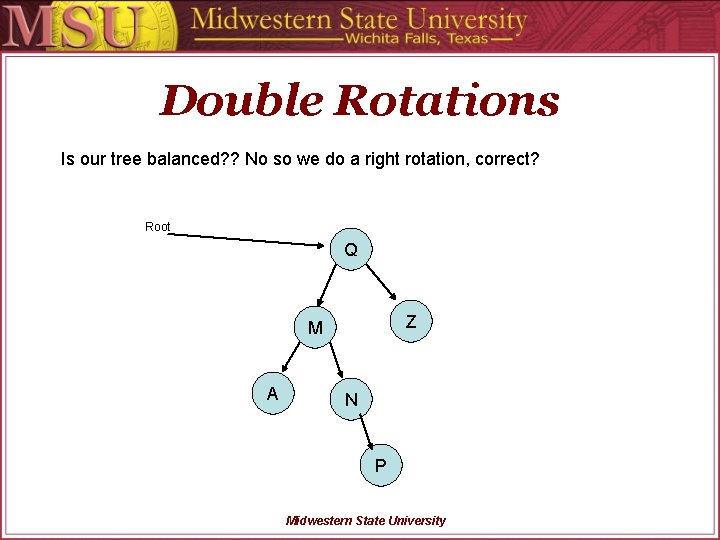
Double Rotations Is our tree balanced? ? No so we do a right rotation, correct? Root Q Z M A N P Midwestern State University

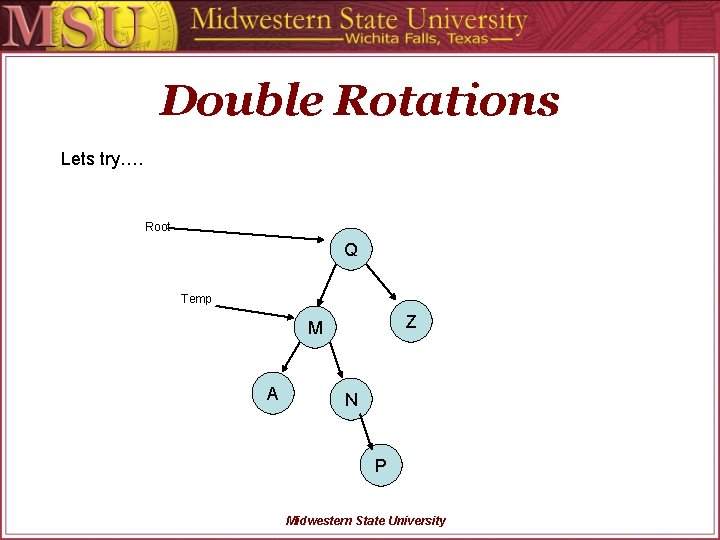
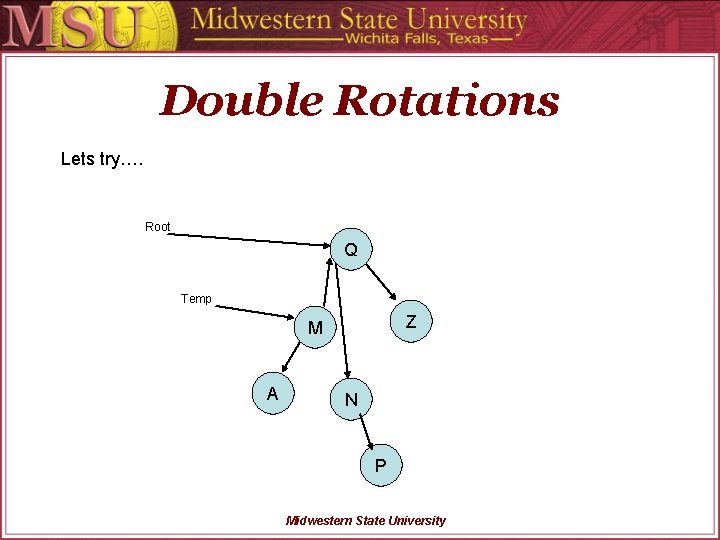
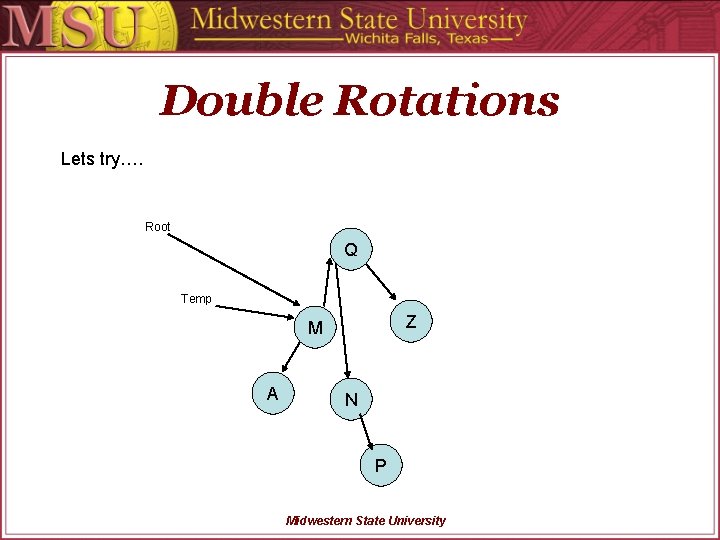
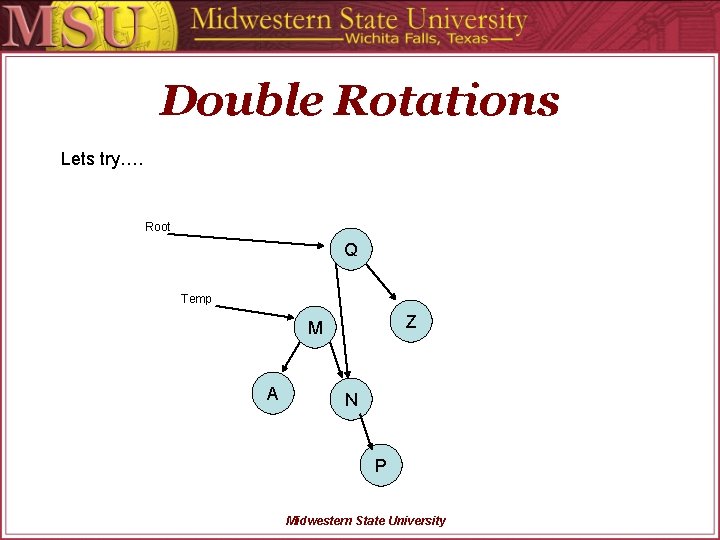
Double Rotations Lets try…. Root Q Temp Z M A N P Midwestern State University

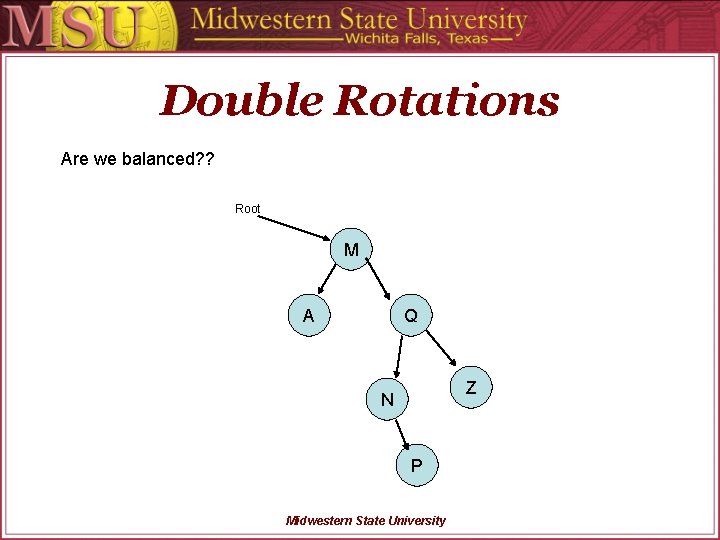
Double Rotations Are we balanced? ? Root M A Q Z N P Midwestern State University

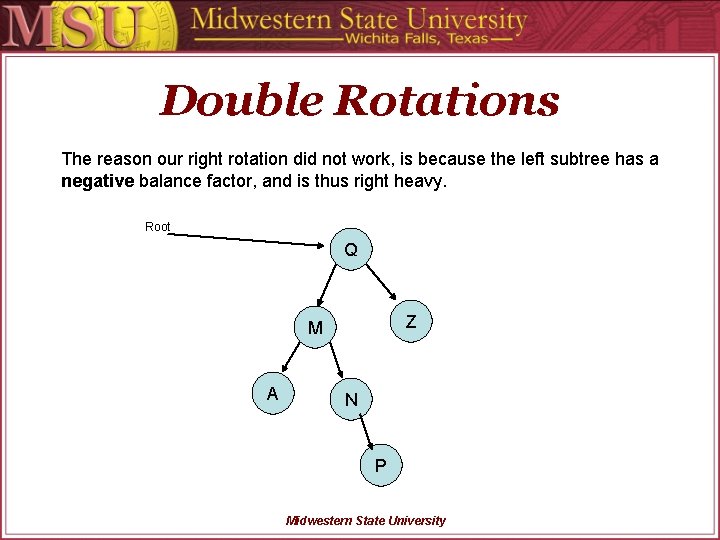
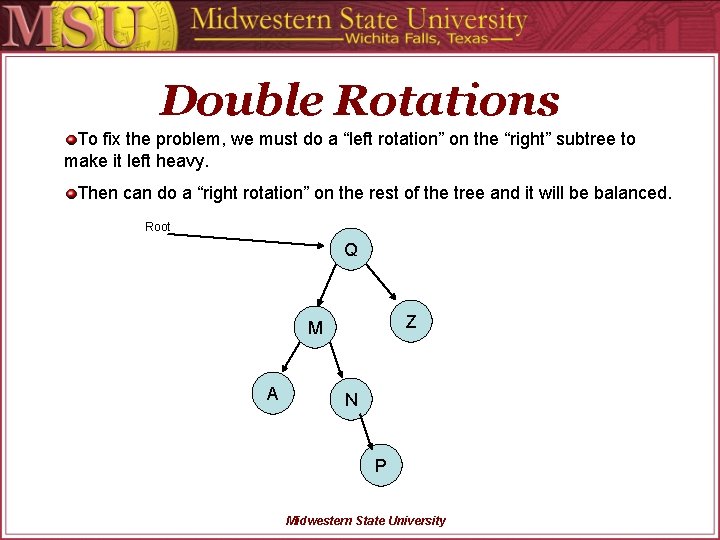
Double Rotations The reason our right rotation did not work, is because the left subtree has a negative balance factor, and is thus right heavy. Root Q Z M A N P Midwestern State University

Double Rotations To fix the problem, we must do a “left rotation” on the “right” subtree to make it left heavy. Then can do a “right rotation” on the rest of the tree and it will be balanced. Root Q Z M A N P Midwestern State University

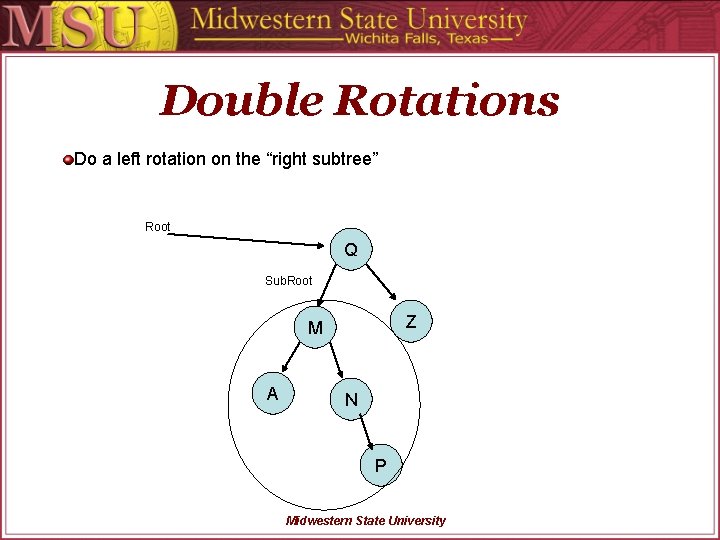
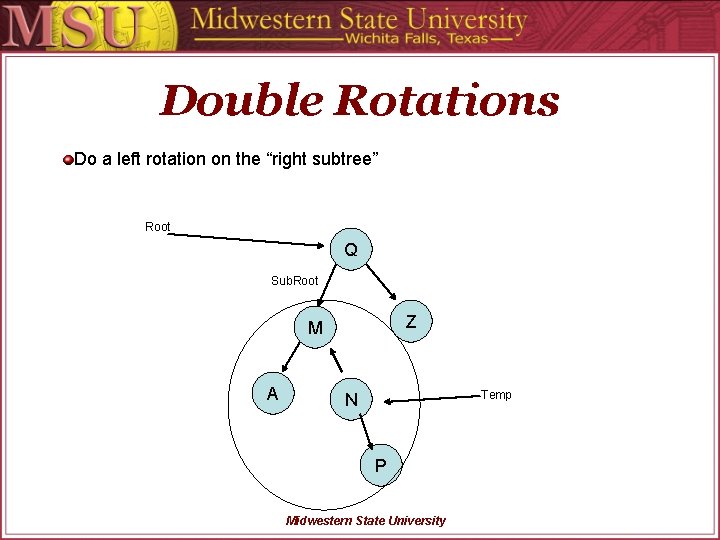
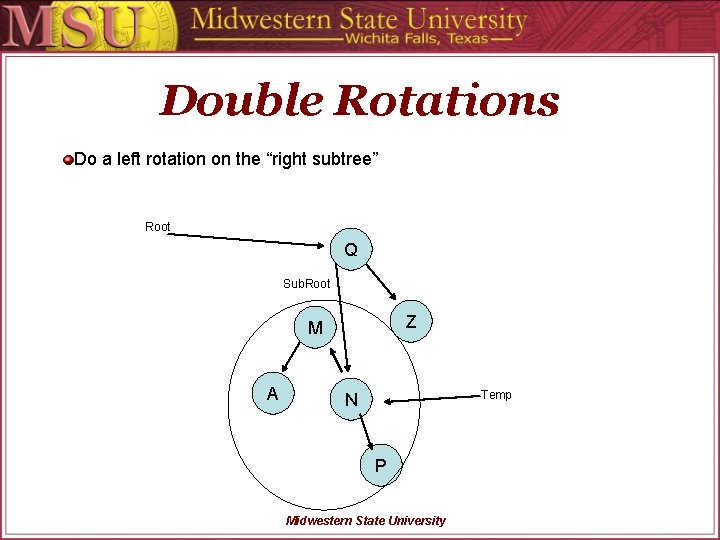
Double Rotations Do a left rotation on the “right subtree” Root Q Sub. Root Z M A N P Midwestern State University

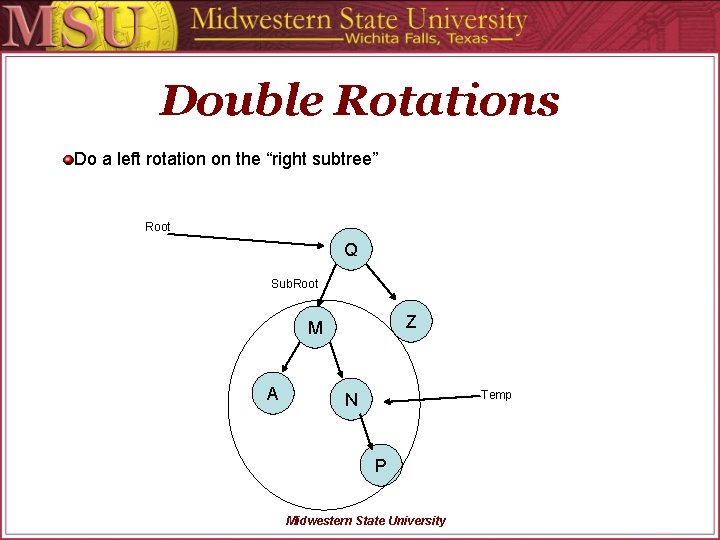
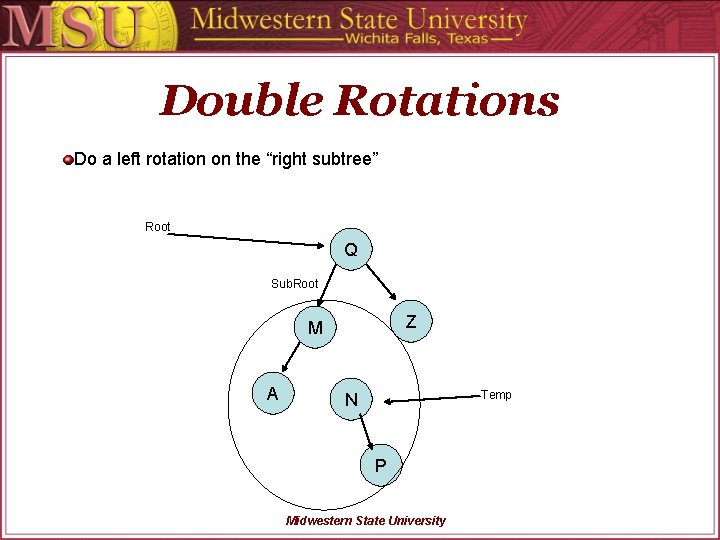
Double Rotations Do a left rotation on the “right subtree” Root Q Sub. Root Z M A Temp N P Midwestern State University

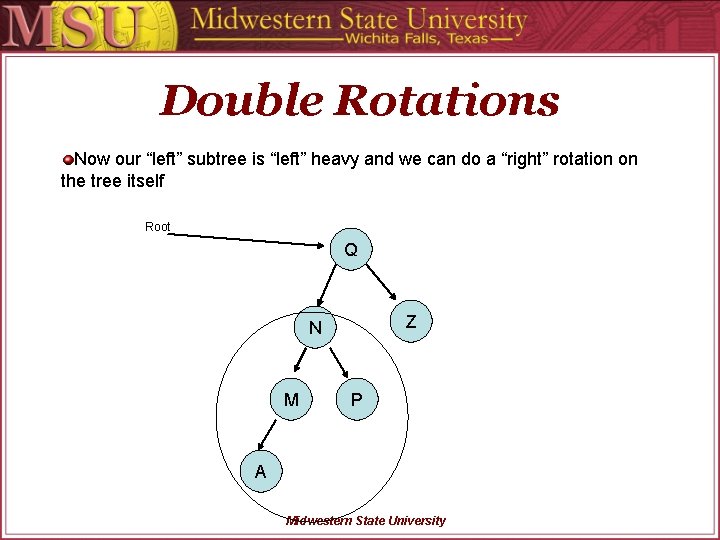
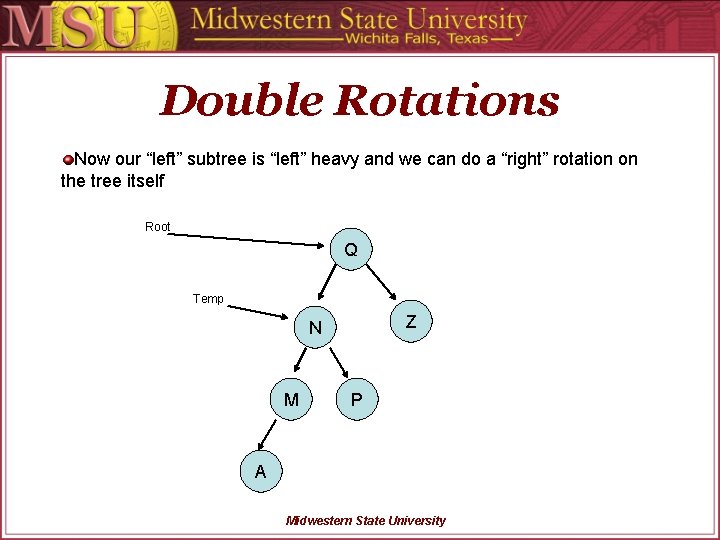
Double Rotations Now our “left” subtree is “left” heavy and we can do a “right” rotation on the tree itself Root Q Z N M P A Midwestern State University

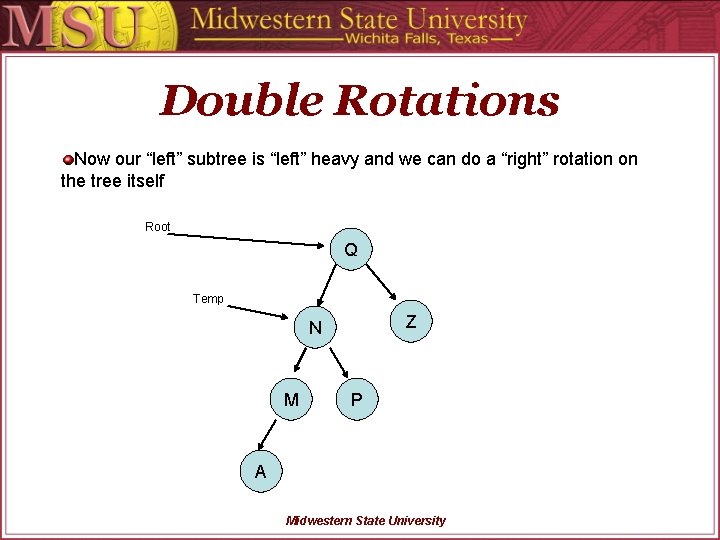
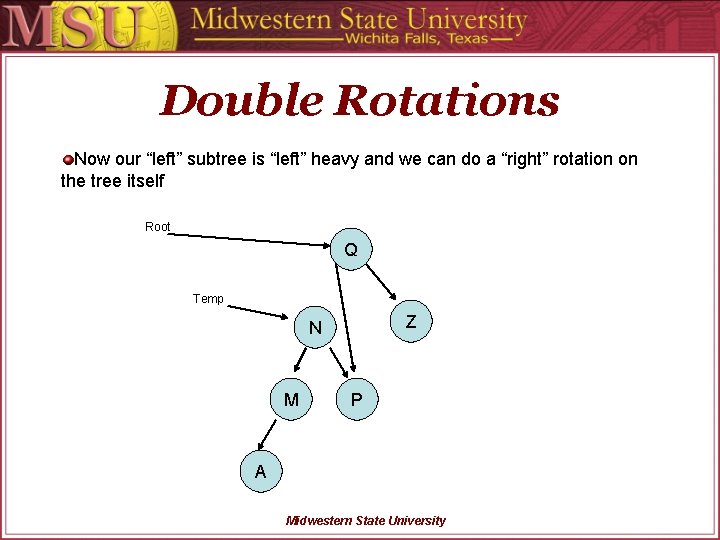
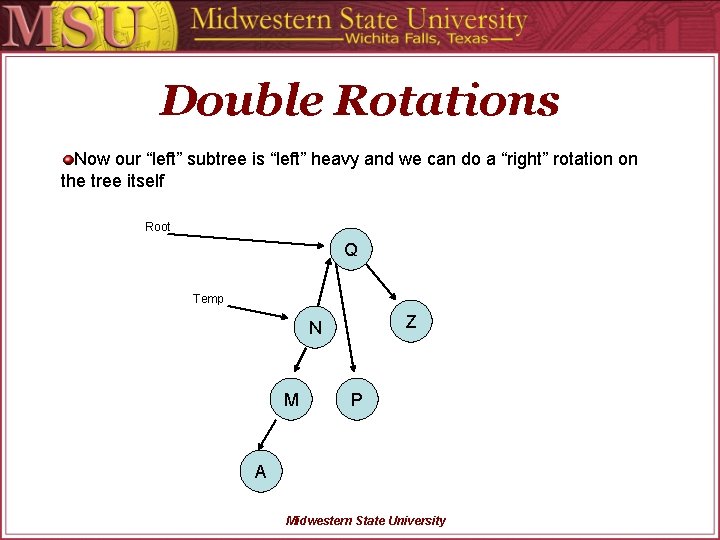
Double Rotations Now our “left” subtree is “left” heavy and we can do a “right” rotation on the tree itself Root Q Temp Z N M P A Midwestern State University

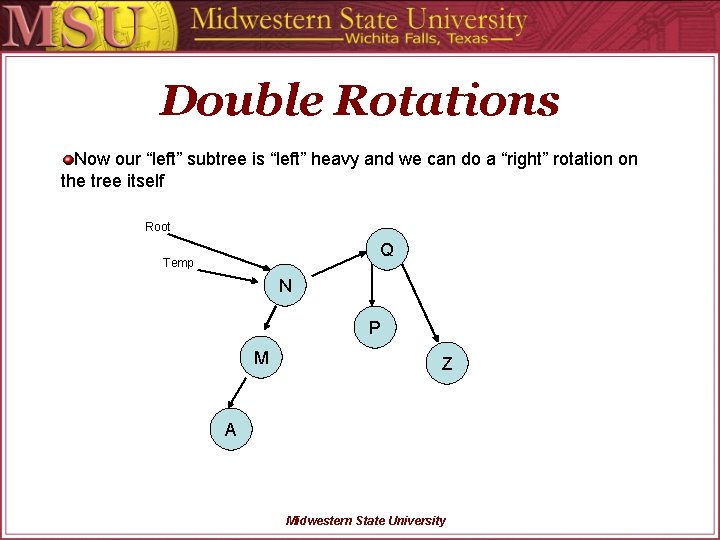
Double Rotations Now our “left” subtree is “left” heavy and we can do a “right” rotation on the tree itself Root Q Temp N P M Z A Midwestern State University

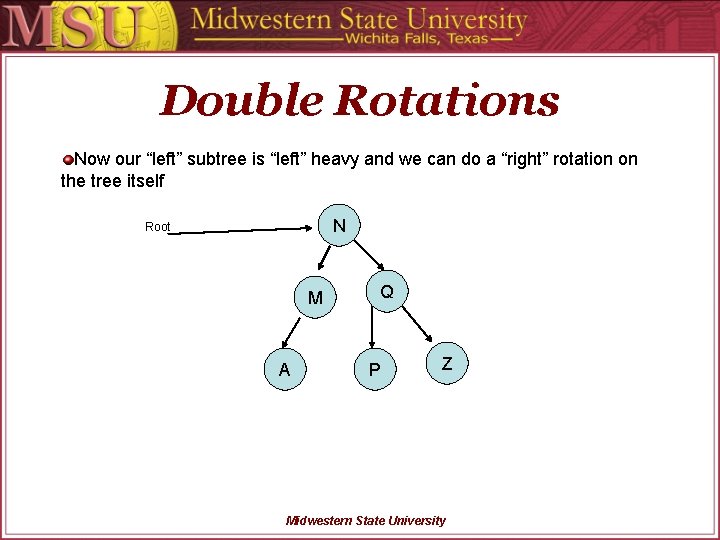
Double Rotations Now our “left” subtree is “left” heavy and we can do a “right” rotation on the tree itself N Root M A Q P Z Midwestern State University

Double Rotations void Avl. Tree: : Rotate. Left(Tree. Node *&Sub. Root){ if(Left. Heavy(Sub. Root->right)){ Rotate. Right(Sub. Root->right); } Tree. Node *Temp; Temp = Sub. Root->right; Sub. Root->right = Temp->left; Temp->left = Sub. Root; Sub. Root = Temp; void Avl. Tree: : Rotate. Right(Tree. Node *&Sub. Root){ if(Right. Heavy(Sub. Root->left)){ Compute. Avl. Values(Sub. Root); Rotate. Left(Sub. Root->left); } } Tree. Node *Temp; Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); } Midwestern State University

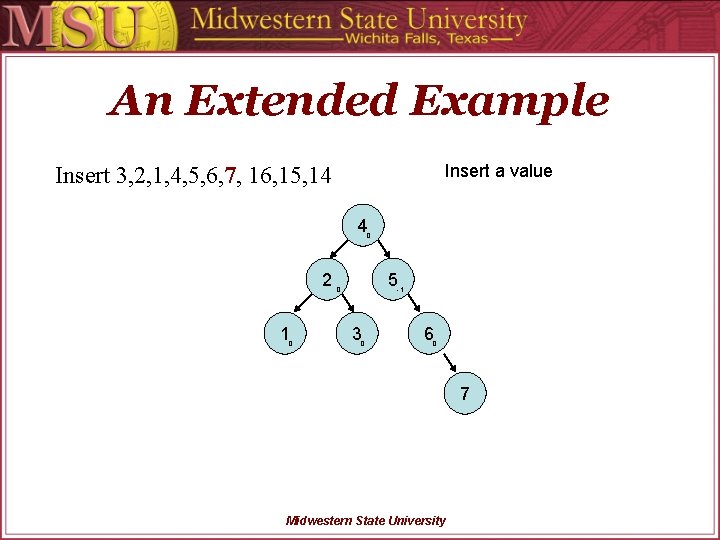
An Extended Example Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 Midwestern State University

An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 Midwestern State University

An Extended Example Calculate Balance Factor Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 0 Midwestern State University

An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 0 2 Midwestern State University

An Extended Example Calculate Balance Factors Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 1 2 0 Midwestern State University

An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 1 2 0 1 Midwestern State University

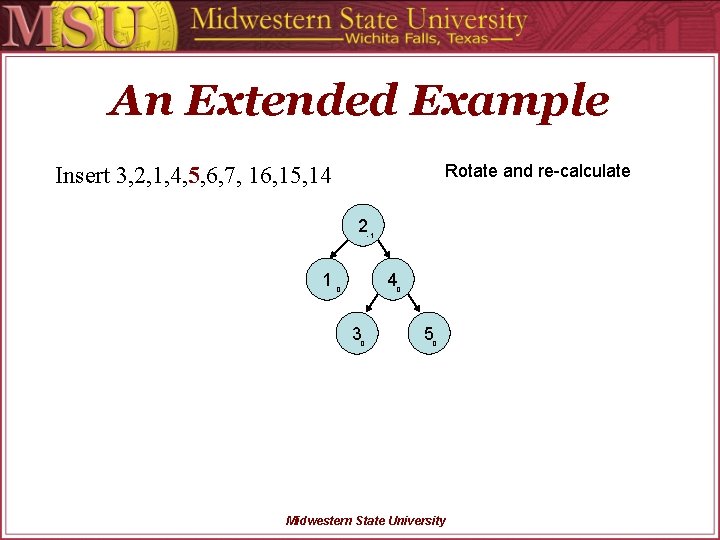
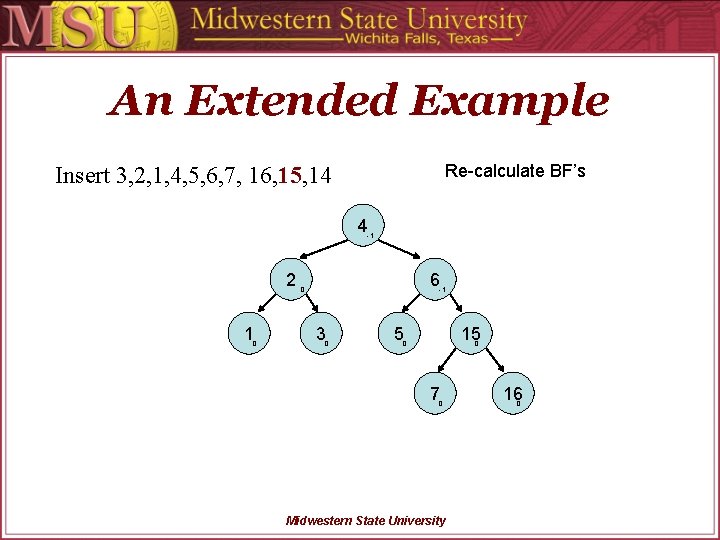
An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 3 2 2 1 1 0 Tree. Node *Temp; Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); Midwestern State University

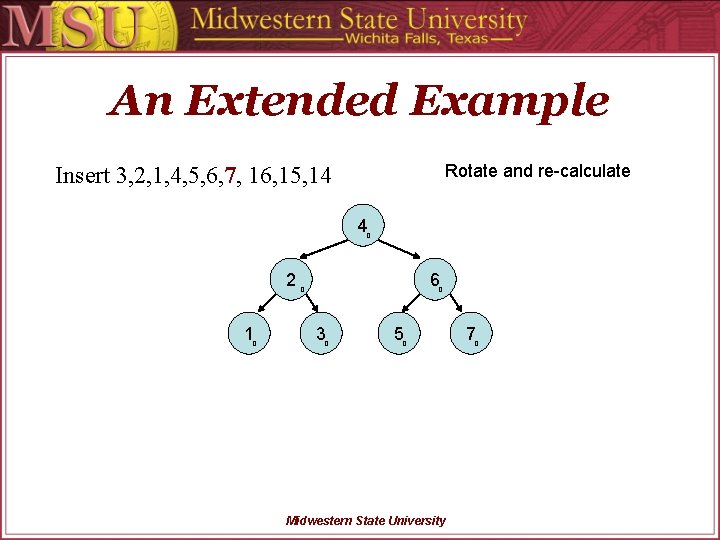
An Extended Example Rotate and re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 0 1 0 3 0 Midwestern State University

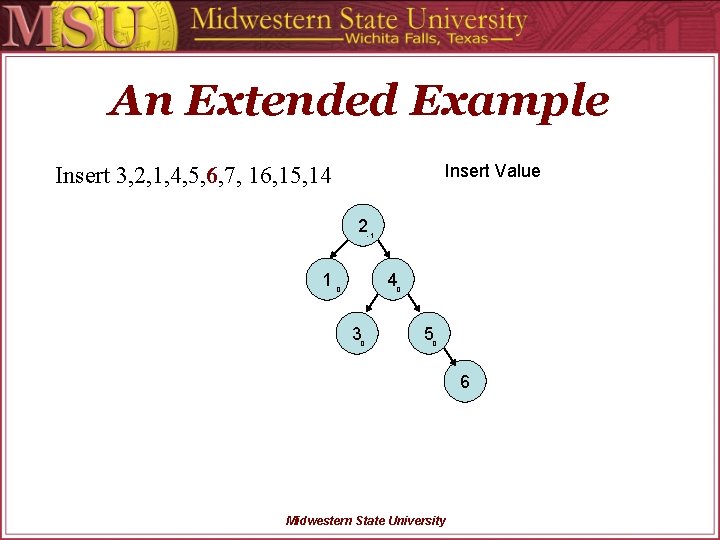
An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 0 1 0 3 0 4 Midwestern State University

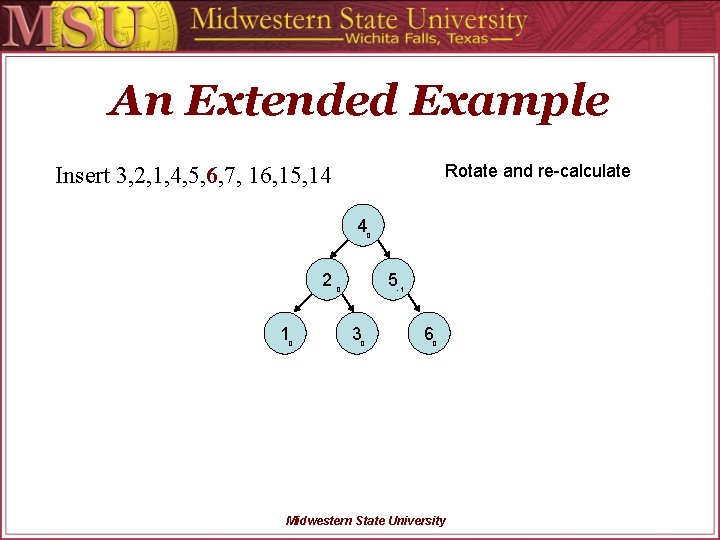
An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 -1 1 0 3 -1 4 0 Midwestern State University

An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 -1 1 0 3 -1 4 0 5 Midwestern State University

An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 -1 1 0 3 -2 4 -1 5 0 Midwestern State University

An Extended Example Rotate and re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 -1 1 4 0 0 3 0 5 0 Midwestern State University

An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 -1 1 4 0 0 3 0 5 0 6 Midwestern State University

An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 2 -2 1 4 0 -1 3 0 5 -1 6 0 Midwestern State University

An Extended Example Rotate and re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 0 2 1 0 5 0 -1 3 0 6 0 Midwestern State University

An Extended Example Insert a value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 0 2 1 0 5 0 -1 3 0 6 0 7 Midwestern State University

An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 0 2 1 0 5 0 -2 3 0 6 -1 7 0 Midwestern State University

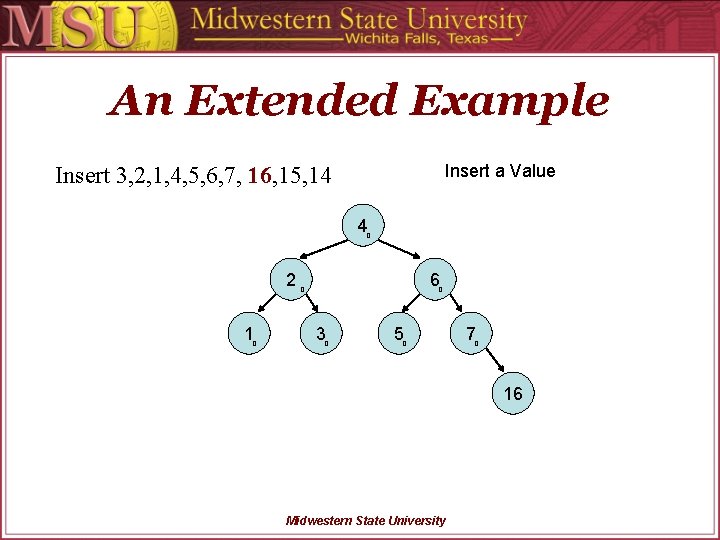
An Extended Example Rotate and re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 0 2 1 0 6 0 0 3 0 5 0 Midwestern State University 7 0

An Extended Example Insert a Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 0 2 1 0 6 0 0 3 0 5 0 7 0 16 Midwestern State University

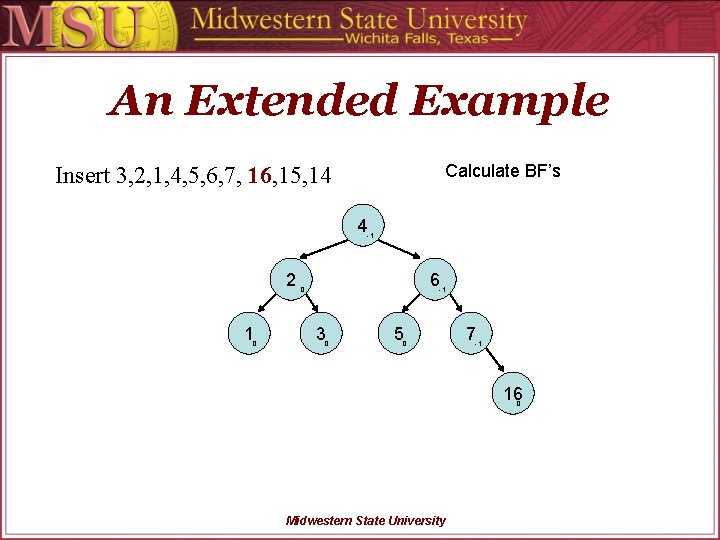
An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -1 3 0 5 0 7 -1 16 0 Midwestern State University

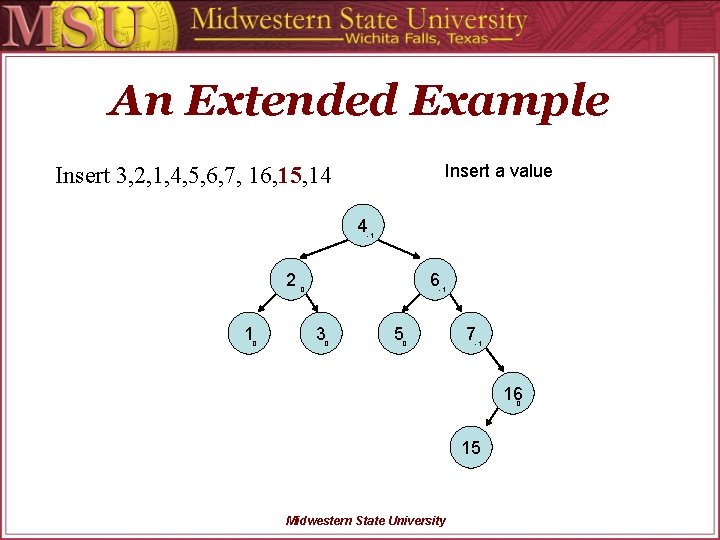
An Extended Example Insert a value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -1 3 0 5 0 7 -1 16 0 15 Midwestern State University

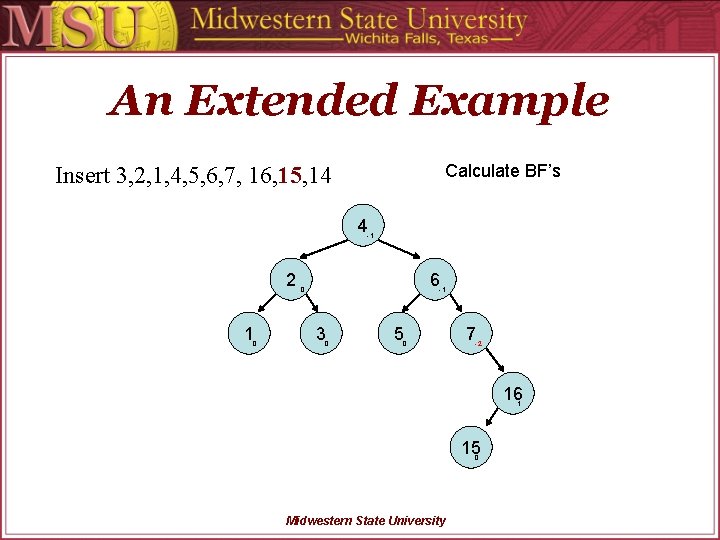
An Extended Example Calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -1 3 0 5 0 7 -2 16 1 15 0 Midwestern State University

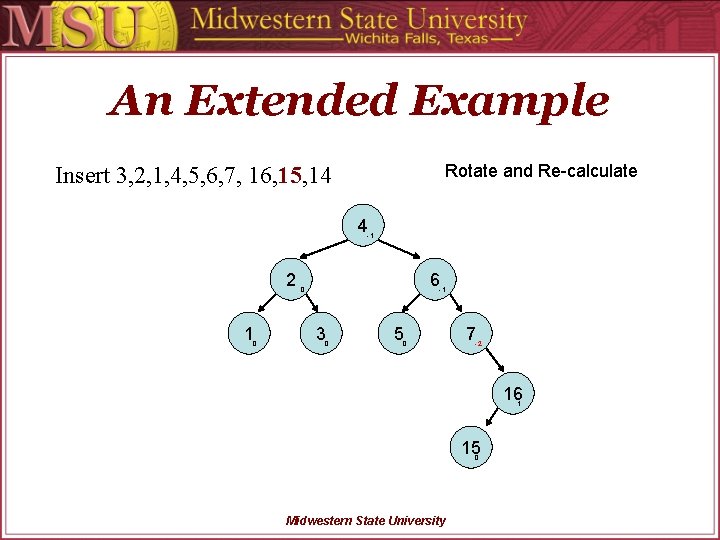
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -1 3 0 5 0 7 -2 16 1 15 0 Midwestern State University

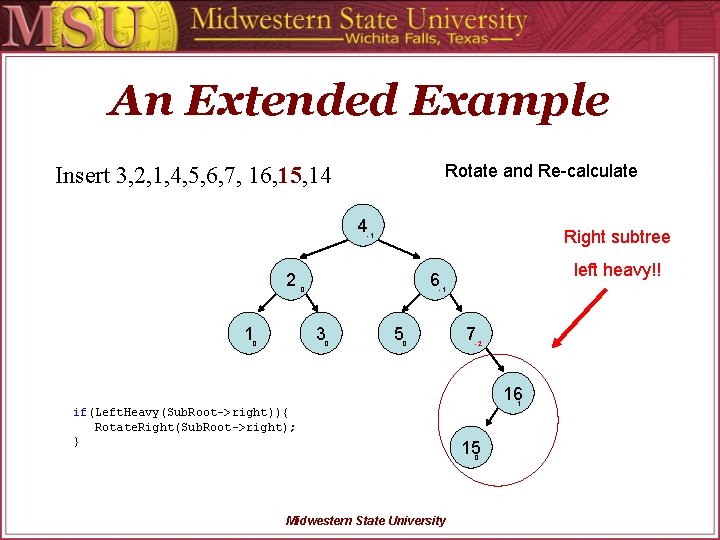
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 Right subtree -1 2 1 0 -1 3 0 left heavy!! 6 0 5 0 7 -2 16 if(Left. Heavy(Sub. Root->right)){ Rotate. Right(Sub. Root->right); } 1 15 0 Midwestern State University

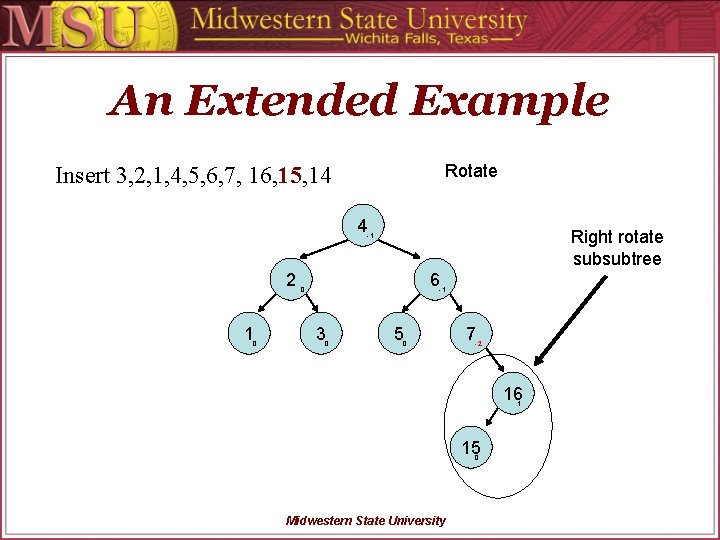
An Extended Example Rotate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 Right rotate subsubtree -1 2 1 0 6 0 -1 3 0 5 0 7 -2 16 1 15 0 Midwestern State University

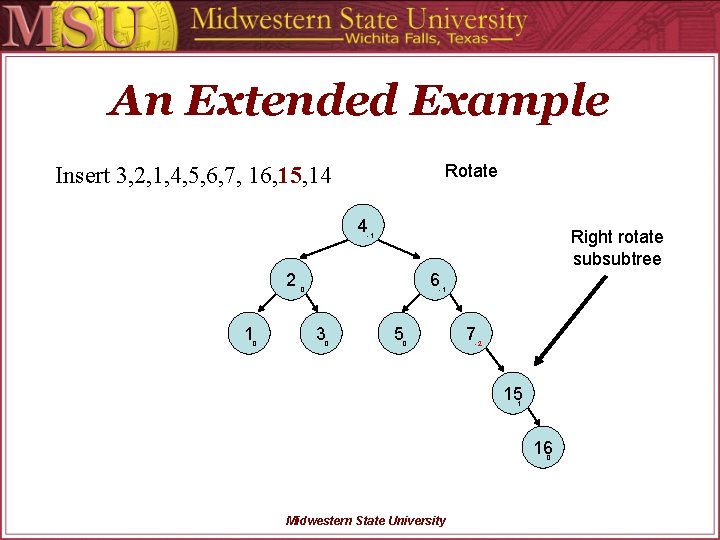
An Extended Example Rotate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 Right rotate subsubtree -1 2 1 0 6 0 -1 3 0 5 0 7 -2 15 1 16 0 Midwestern State University

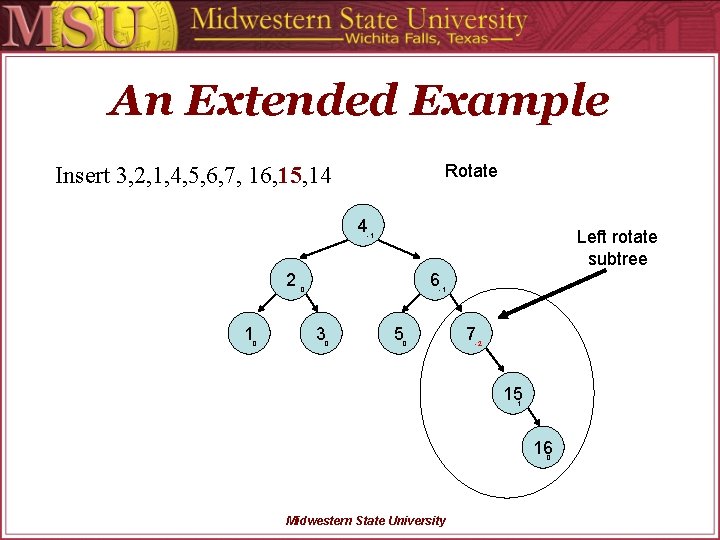
An Extended Example Rotate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 Left rotate subtree -1 2 1 0 6 0 -1 3 0 5 0 7 -2 15 1 16 0 Midwestern State University

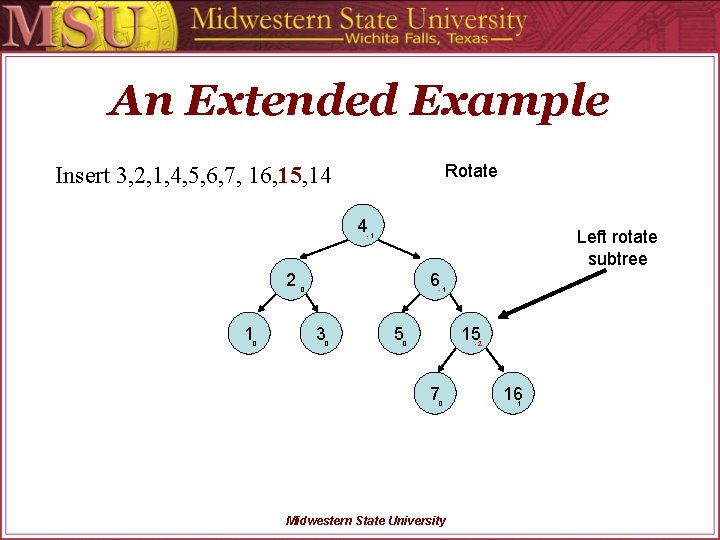
An Extended Example Rotate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 Left rotate subtree -1 2 1 0 6 0 -1 3 0 5 15 0 -2 7 0 Midwestern State University 16 1

An Extended Example Re-calculate BF’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -1 3 0 5 15 0 0 7 0 Midwestern State University 16 0

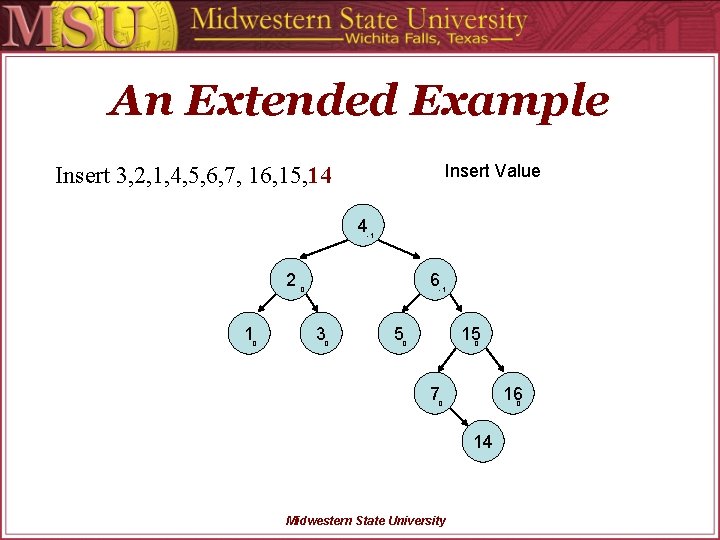
An Extended Example Insert Value Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -1 3 0 5 15 0 0 7 16 0 0 14 Midwestern State University

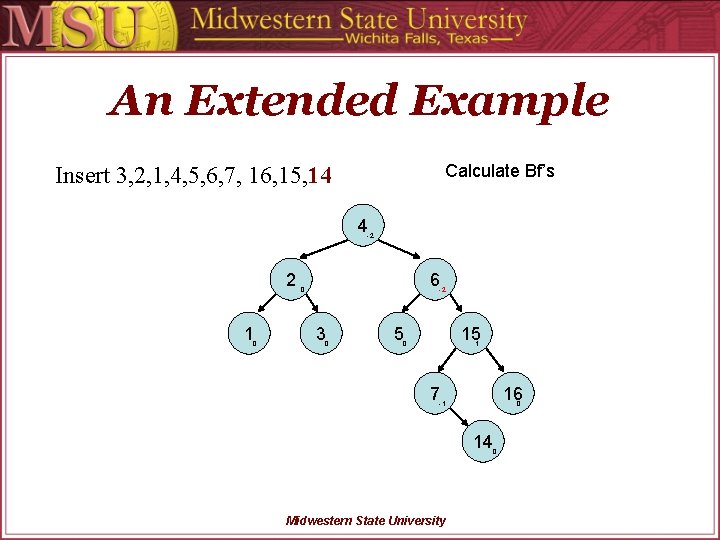
An Extended Example Calculate Bf’s Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -2 2 1 0 6 0 -2 3 0 5 15 0 1 7 16 -1 0 14 Midwestern State University 0

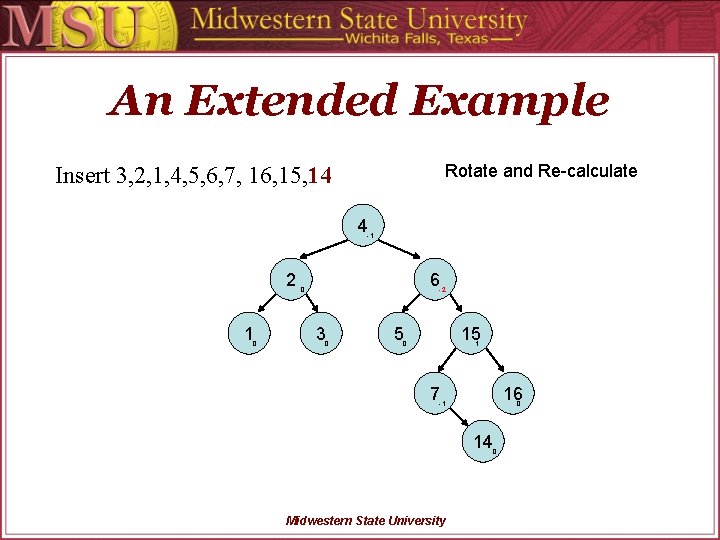
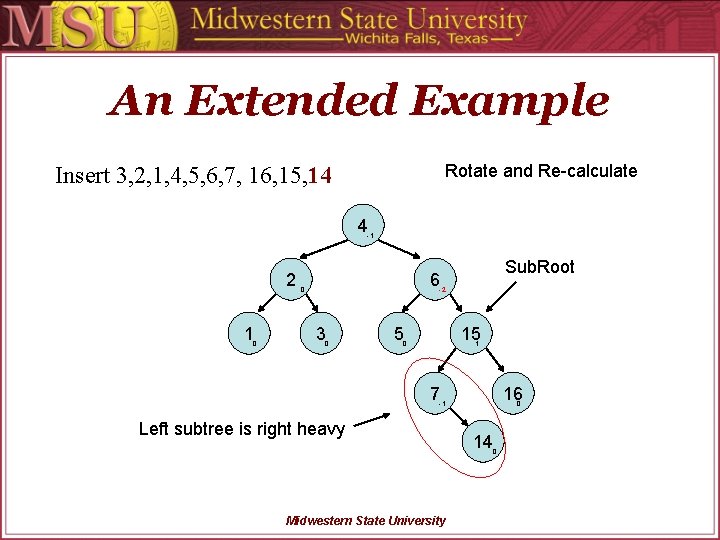
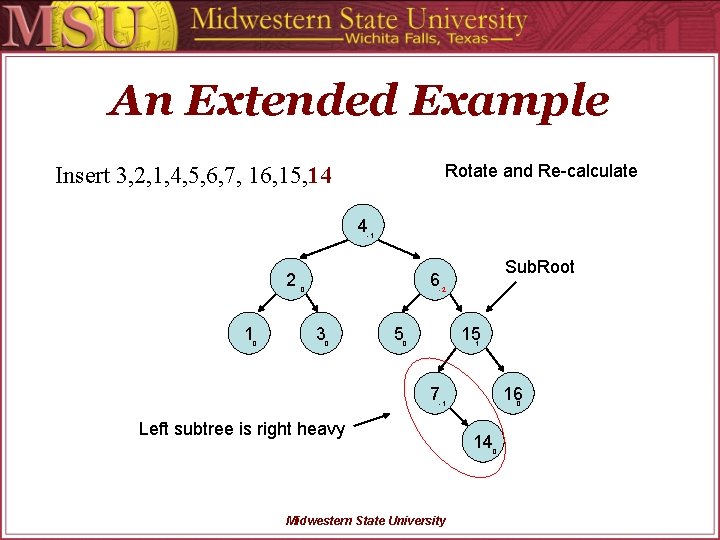
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -2 3 0 5 15 0 1 7 16 -1 0 14 Midwestern State University 0

An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 Sub. Root 6 0 -2 3 0 5 15 0 1 7 16 -1 Left subtree is right heavy Midwestern State University 0 14 0

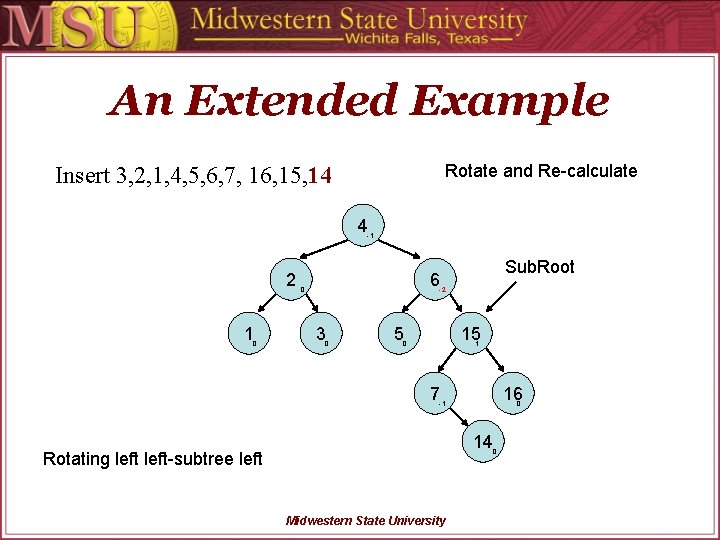
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 Sub. Root 6 0 -2 3 0 5 15 0 1 7 16 -1 0 14 Rotating left-subtree left Midwestern State University 0

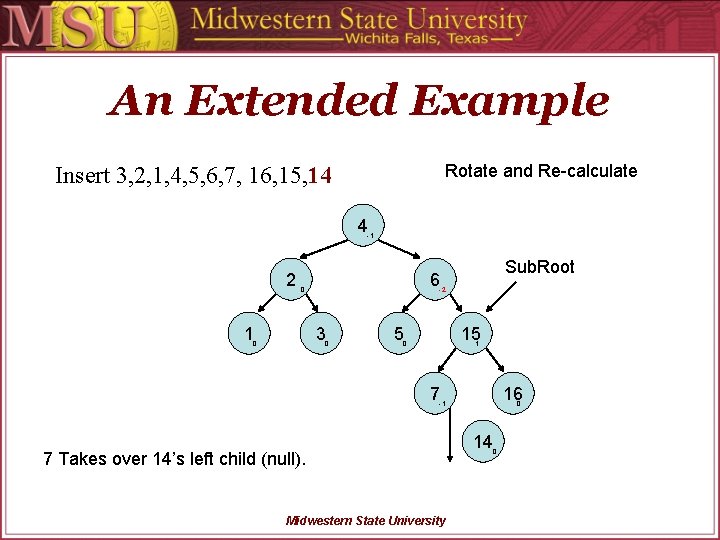
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 0 1 -2 3 0 Sub. Root 6 0 5 15 0 1 7 16 -1 7 Takes over 14’s left child (null). Midwestern State University 0 14 0

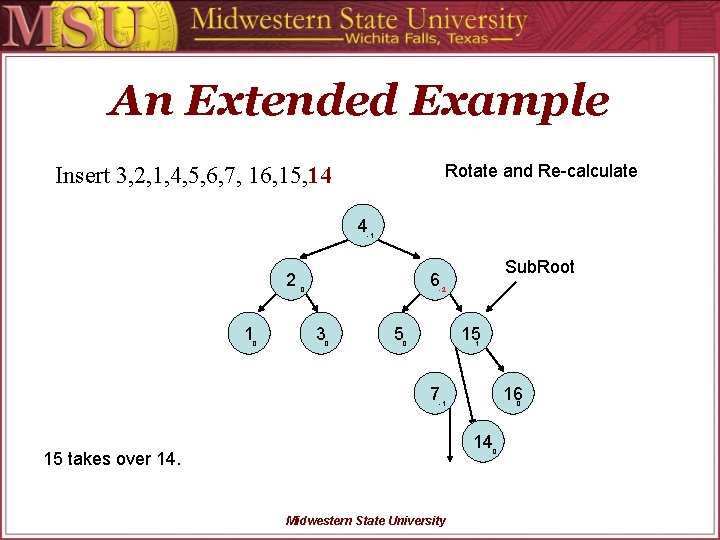
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 Sub. Root 6 0 -2 3 0 5 15 0 1 7 16 -1 0 14 15 takes over 14. Midwestern State University 0

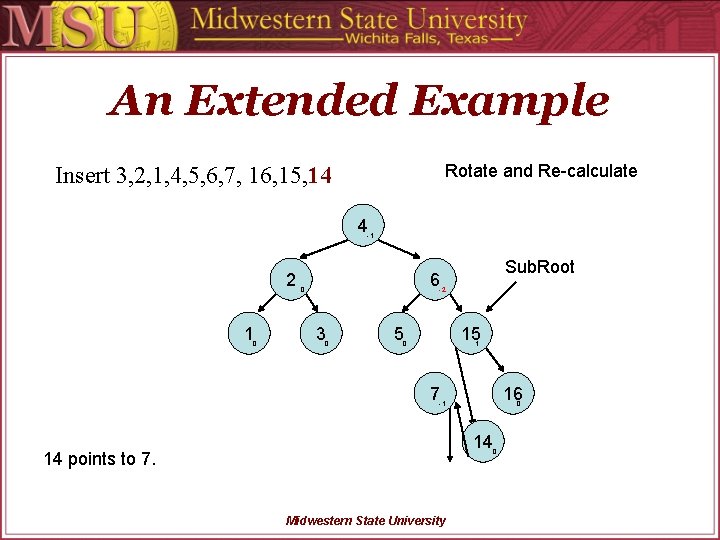
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 Sub. Root 6 0 -2 3 0 5 15 0 1 7 16 -1 0 14 14 points to 7. Midwestern State University 0

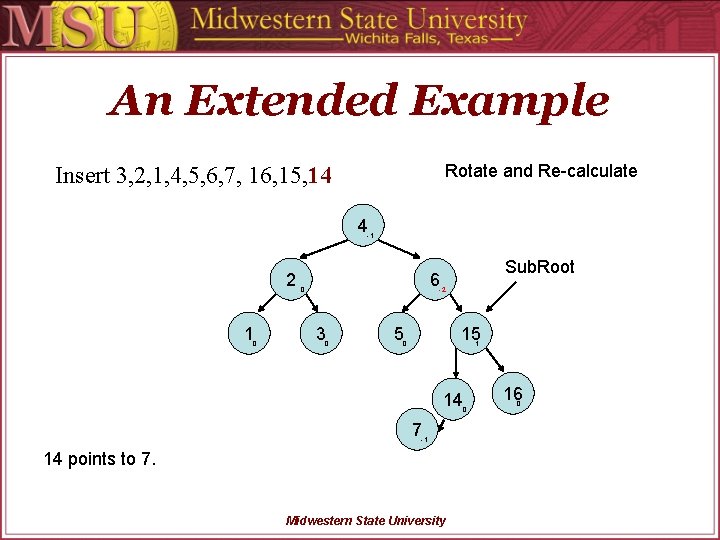
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 Sub. Root 6 0 -2 3 0 5 15 0 1 14 7 -1 14 points to 7. Midwestern State University 16 0 0

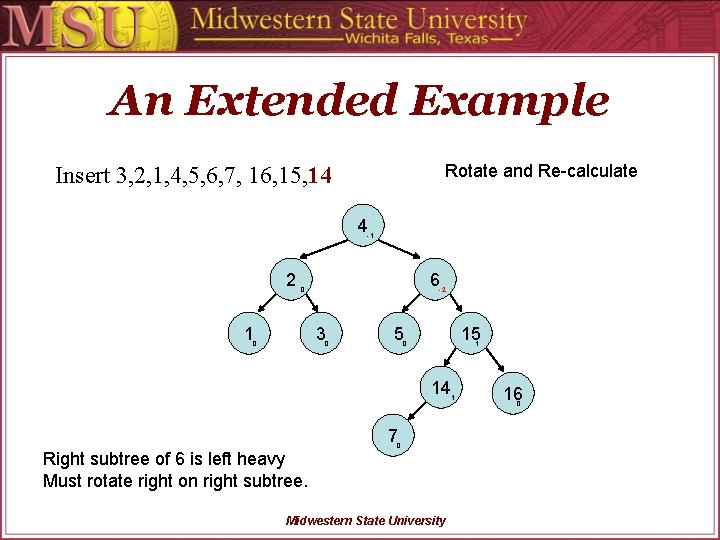
An Extended Example Rotate and Re-calculate Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 6 0 1 -2 3 0 0 5 15 0 1 14 7 Right subtree of 6 is left heavy Must rotate right on right subtree. 0 Midwestern State University 1 16 0

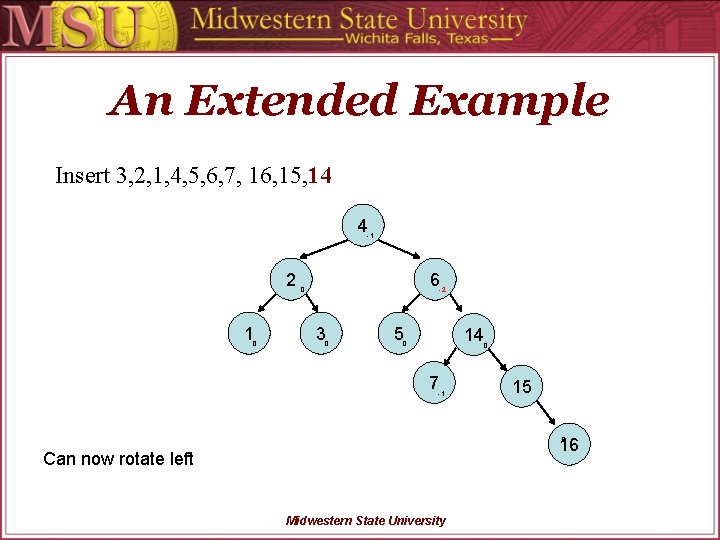
An Extended Example Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 6 0 -2 3 0 5 14 0 1 0 7 -1 15 16 0 Can now rotate left Midwestern State University

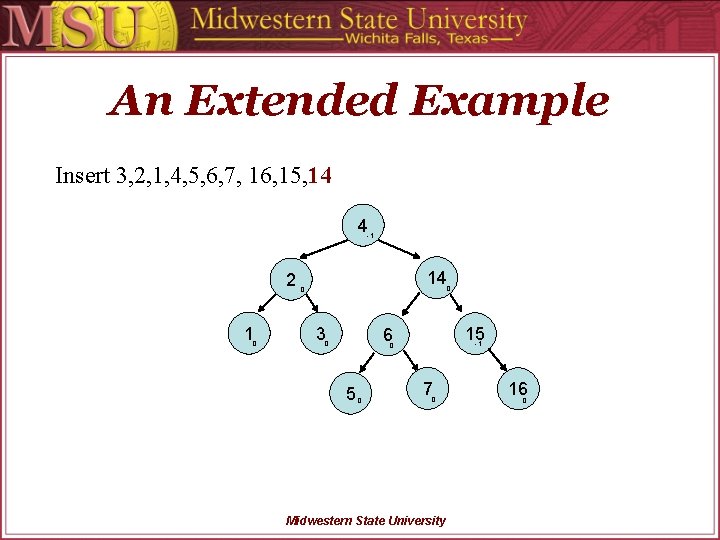
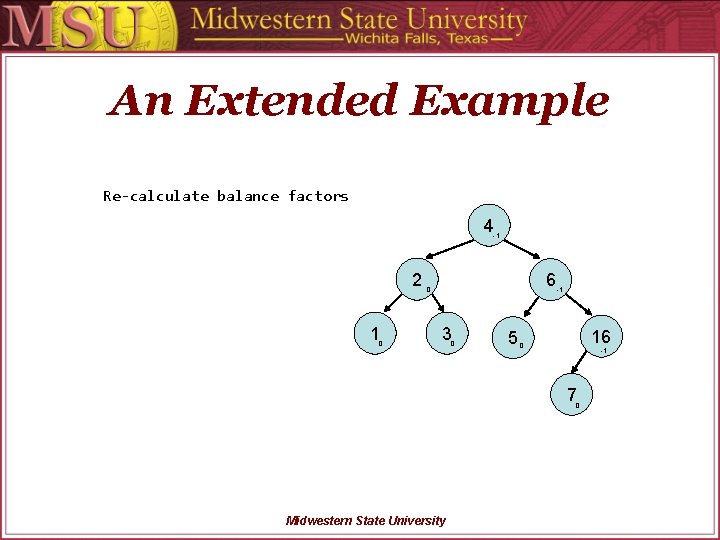
An Extended Example Insert 3, 2, 1, 4, 5, 6, 7, 16, 15, 14 4 -1 2 1 0 14 0 3 15 6 0 -1 0 5 0 0 7 0 Midwestern State University 16 0

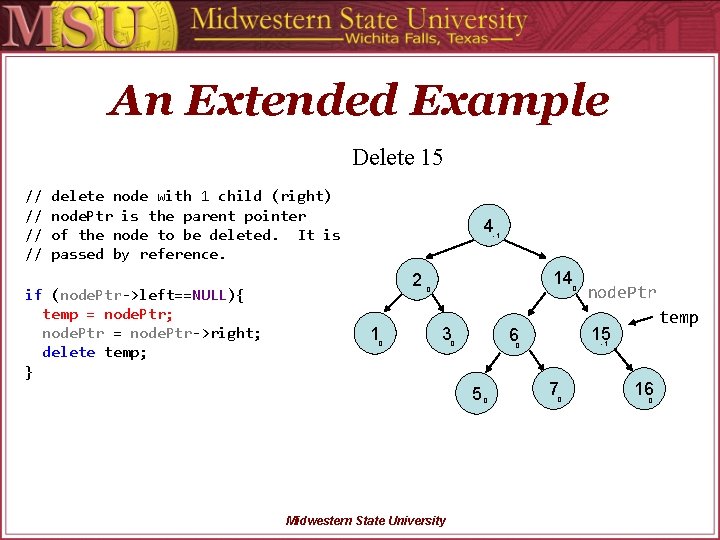
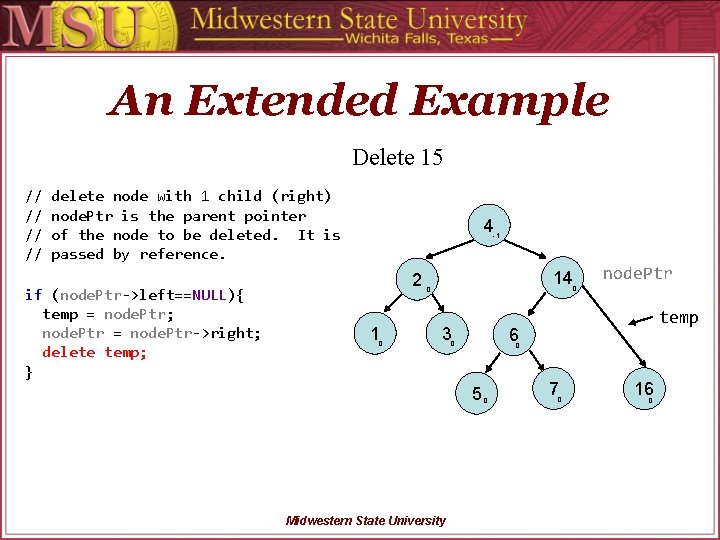
An Extended Example Delete 15 // // delete node with 1 child (right) node. Ptr is the parent pointer of the node to be deleted. It is passed by reference. if (node. Ptr->left==NULL){ temp = node. Ptr; node. Ptr = node. Ptr->right; delete temp; } 4 -1 2 1 0 14 0 3 Midwestern State University 0 temp -1 0 5 node. Ptr 15 6 0 0 7 0 16 0

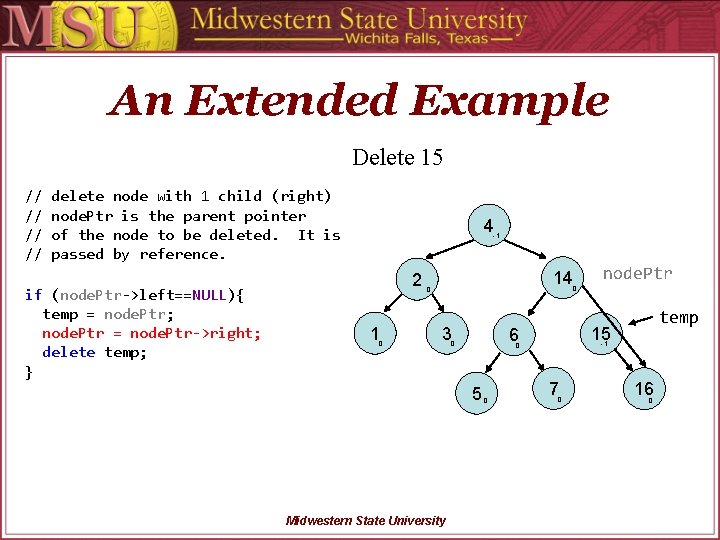
An Extended Example Delete 15 // // delete node with 1 child (right) node. Ptr is the parent pointer of the node to be deleted. It is passed by reference. if (node. Ptr->left==NULL){ temp = node. Ptr; node. Ptr = node. Ptr->right; delete temp; } 4 -1 2 1 0 14 0 3 temp 6 0 0 5 Midwestern State University node. Ptr 0 0 7 0 16 0

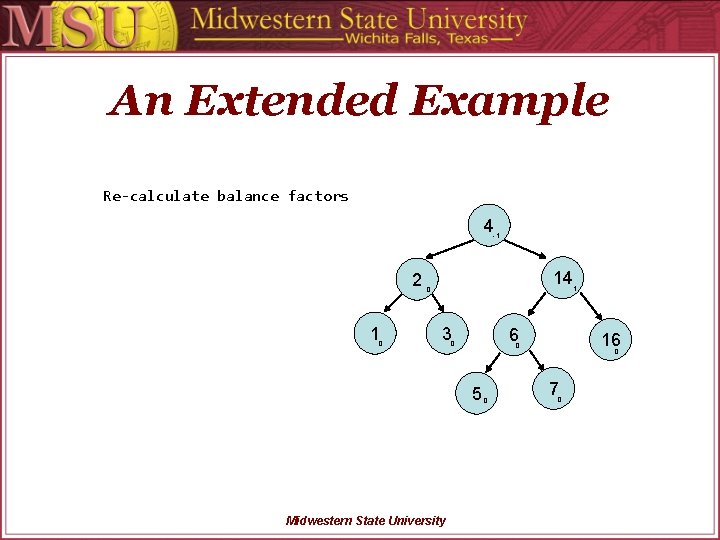
An Extended Example Re-calculate balance factors 4 -1 2 1 0 14 0 3 6 0 Midwestern State University 16 0 5 0 1 0 7 0

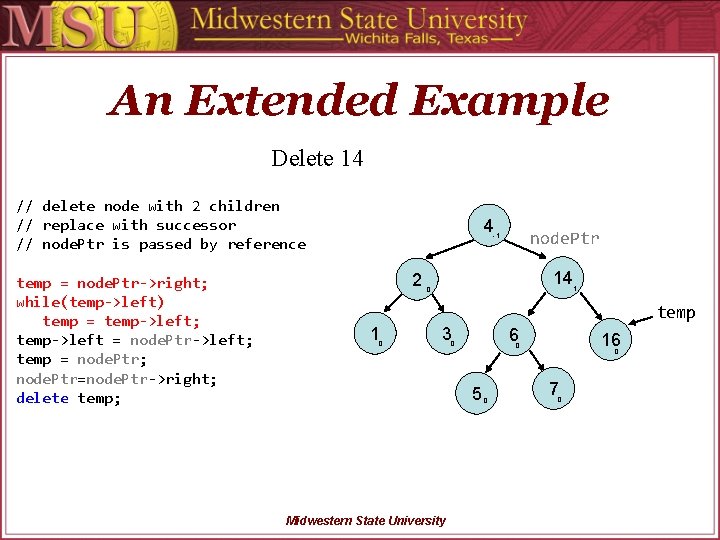
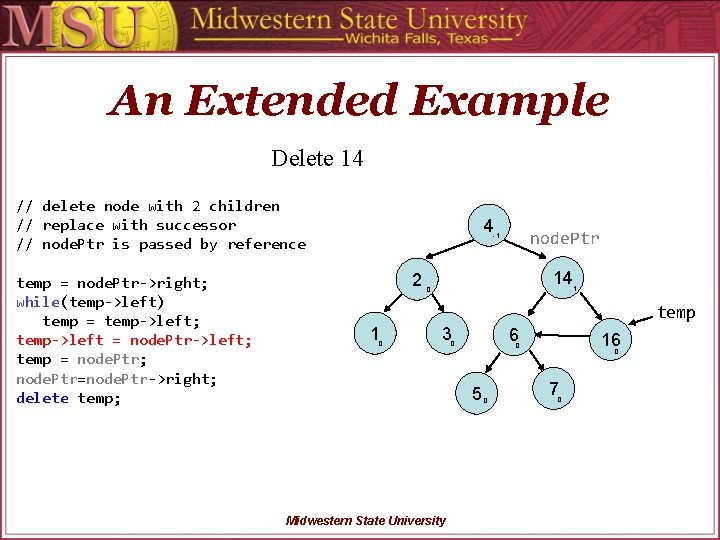
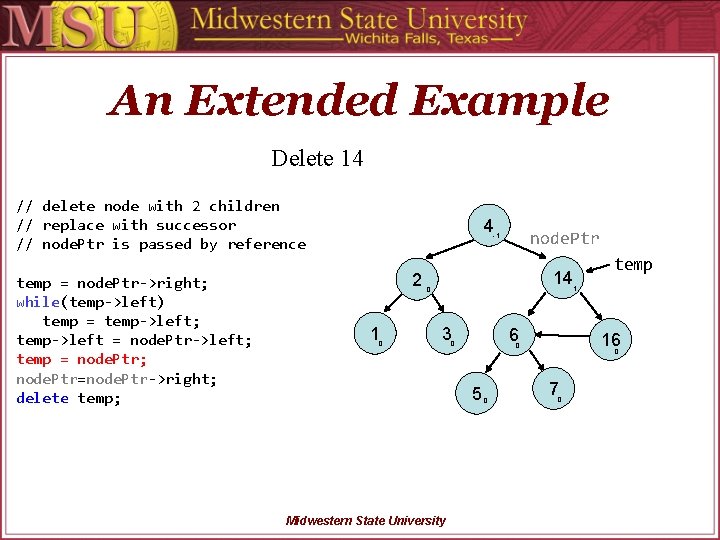
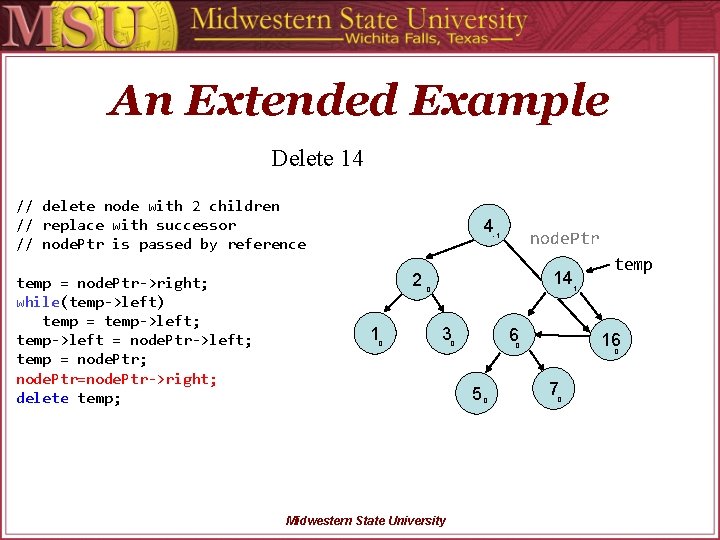
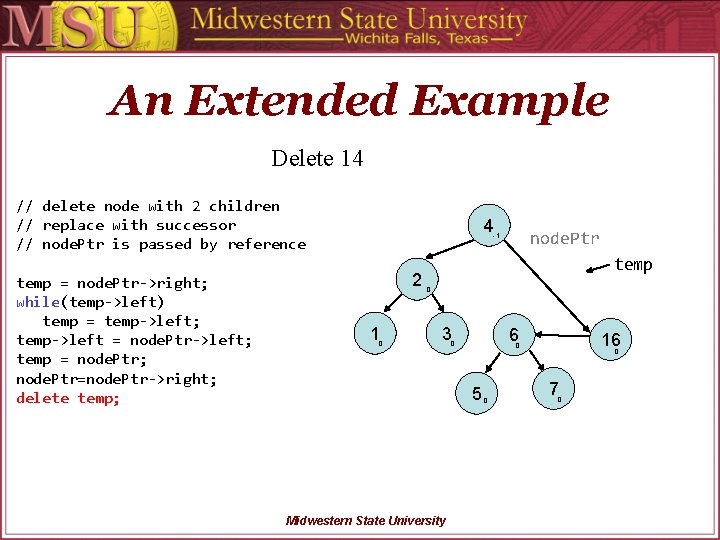
An Extended Example Delete 14 // delete node with 2 children // replace with successor // node. Ptr is passed by reference temp = node. Ptr->right; while(temp->left) temp = temp->left; temp->left = node. Ptr->left; temp = node. Ptr; node. Ptr=node. Ptr->right; delete temp; 4 node. Ptr -1 2 14 0 1 temp 1 0 3 6 0 5 Midwestern State University 16 0 0 0 7 0

An Extended Example Delete 14 // delete node with 2 children // replace with successor // node. Ptr is passed by reference temp = node. Ptr->right; while(temp->left) temp = temp->left; temp->left = node. Ptr->left; temp = node. Ptr; node. Ptr=node. Ptr->right; delete temp; 4 node. Ptr -1 2 1 0 14 0 3 6 0 Midwestern State University 0 1 16 0 5 temp 0 7 0

An Extended Example Delete 14 // delete node with 2 children // replace with successor // node. Ptr is passed by reference temp = node. Ptr->right; while(temp->left) temp = temp->left; temp->left = node. Ptr->left; temp = node. Ptr; node. Ptr=node. Ptr->right; delete temp; 4 node. Ptr -1 2 1 0 temp 0 3 6 0 5 Midwestern State University 16 0 0 0 7 0

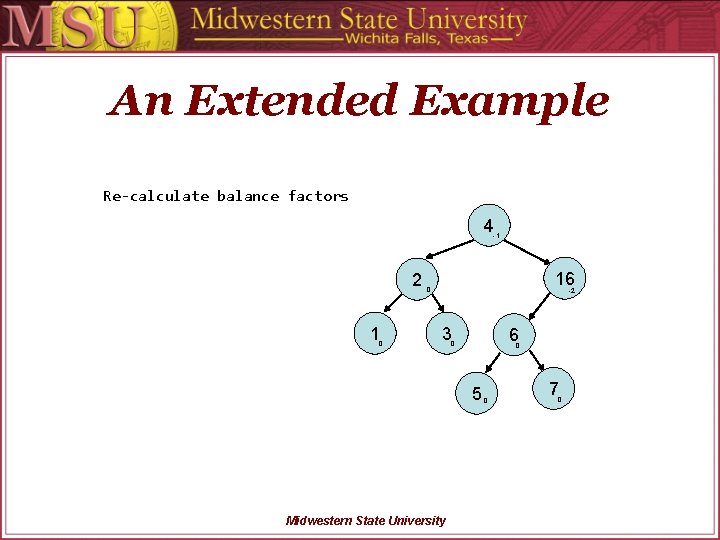
An Extended Example Re-calculate balance factors 4 -1 2 1 0 16 0 -2 3 6 0 0 5 Midwestern State University 0 7 0

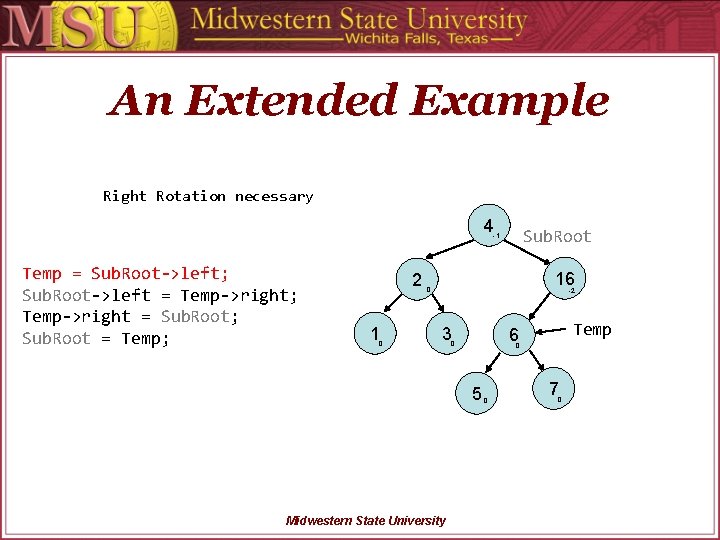
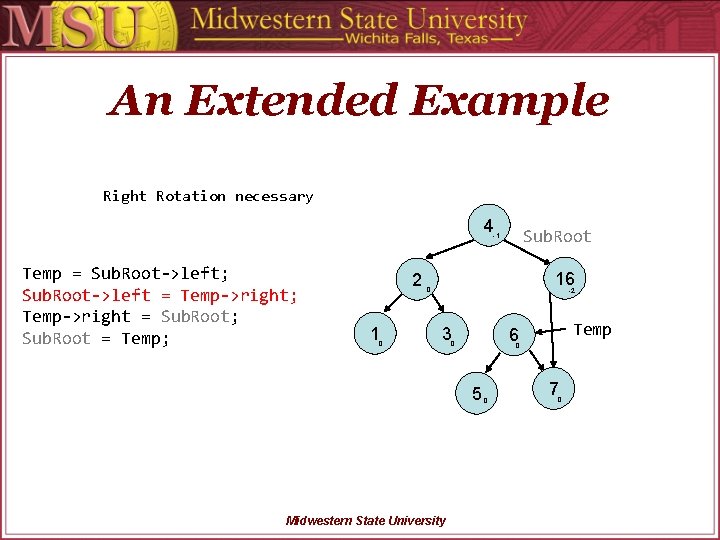
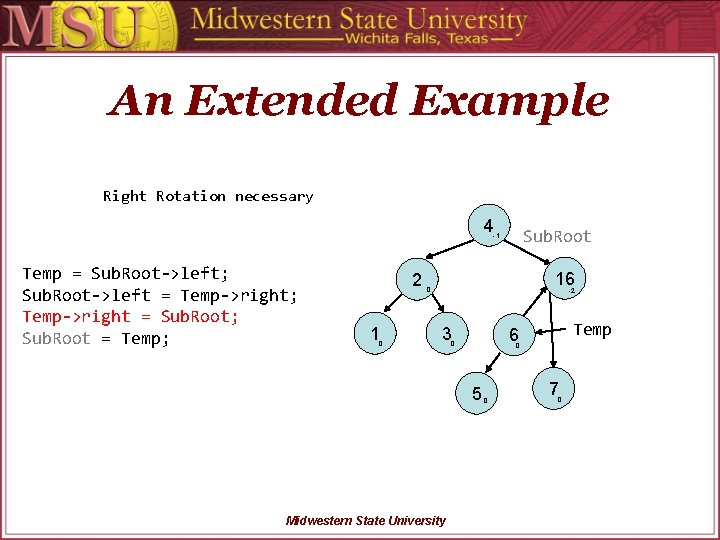
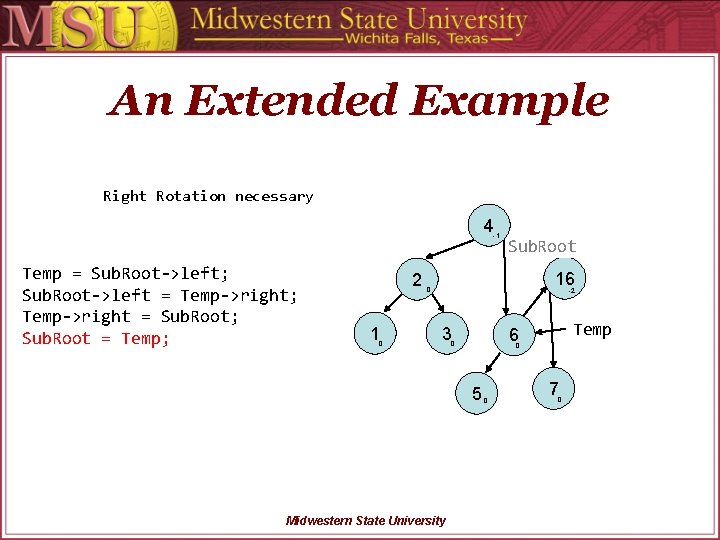
An Extended Example Right Rotation necessary 4 Sub. Root -1 Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; 2 1 0 16 0 -2 3 0 5 Midwestern State University Temp 6 0 0 7 0

An Extended Example Right Rotation necessary 4 -1 Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; 2 1 0 Sub. Root 16 0 -2 3 0 5 Midwestern State University Temp 6 0 0 7 0

An Extended Example Re-calculate balance factors 4 -1 2 1 0 6 0 3 0 5 -1 16 0 -1 7 0 Midwestern State University

AVL Implementation All methods mimic a BST implementation (with one tiny modification: rotations). The addition of rotation keeps the tree balanced (as stated previously) Rotations also add some complexity to the implementation. Midwestern State University

AVL Implementation Methods that “I” (meaning, not necessarily the best implementation) added to maintain the balance factor of each node (aka: AVL rules ) Height – the height of a given tree. Avl. Value – the Avl Value of a tree node. Left. Heavy – Is the left subtree heavier than the right? Right. Heavy – Is the right subtree heavier than the left? Rotate. Left – Performs a left rotation from a given node. Rotate. Right – Performs a right rotation from a given node. Compute. Avl. Values – Computes avl values for entire tree. Midwestern State University

$Height int BSTree: : Height(Tree. Node *node. Ptr){ int left_height=0; int right_height=0; if(node. Ptr==NULL)$

Height int BSTree: : Height(Tree. Node *node. Ptr){ int left_height=0; int right_height=0; if(node. Ptr==NULL) return 0; else{ left_height = Height(node. Ptr->left); right_height = Height(node. Ptr->right); } if(left_height>right_height) return 1+left_height; else return 1+right_height; } int BSTree: : Tree. Height(){ return Height(root); } Midwestern State University

Avl. Value int BSTree: : Avl. Value(Tree. Node *node. Ptr) { int leftheight = Height(node. Ptr->left); int rightheight = Height(node. Ptr->right); return leftheight-rightheight; } Midwestern State University

Left / Right Heavy bool BSTree: : Left. Heavy(Tree. Node * ptr) { return (Height(ptr->left) > Height(ptr->right)); } bool BSTree: : Right. Heavy(Tree. Node * ptr) { return (Height(ptr->right) > Height(ptr->left)); } Midwestern State University

Rotate Left/Right void BSTree: : Rotate. Left(Tree. Node *& Sub. Root) { if (Sub. Root->right != NULL && Left. Heavy(Sub. Root->right)){ Rotate. Right(Sub. Root->right); } } void BSTree: : Rotate. Right(Tree. Node *& Sub. Root) { if (Sub. Root->left != NULL && Right. Heavy(Sub. Root->left)){ Rotate. Left(Sub. Root->left); } Tree. Node *Temp; Temp = Sub. Root->right; Sub. Root->right = Temp->left; Temp->left = Sub. Root; Sub. Root = Temp; Tree. Node *Temp; Temp = Sub. Root->left; Sub. Root->left = Temp->right; Temp->right = Sub. Root; Sub. Root = Temp; Compute. Avl. Values(Sub. Root); } Midwestern State University

Compute. Avl. Values void BSTree: : Compute. Avl. Values(Tree. Node *&node. Ptr) { if(node. Ptr){ Compute. Avl. Values(node. Ptr->left); Compute. Avl. Values(node. Ptr->right); node. Ptr->Avl. Value=Avl. Value(node. Ptr); if (node. Ptr->Avl. Value > 1) Rotate. Right(node. Ptr); else if (node. Ptr->Avl. Value < -1) Rotate. Left(node. Ptr); } } Midwestern State University