AVL Trees AA Trees Balancing Binary Search Trees

AVL Trees, AA Trees Balancing Binary Search Trees, Rotations Tree-Lik Structu e res Soft. Uni Team Technical Trainers Software University http: //softuni. bg

Table of Contents 1. AVL Trees 1. Properties of AVL 2. Rotations in AVL (Double Left, Double Right) 3. AVL Insertion Algorithm 2. AA Trees 1. Properties of AA 2. Rotations in AA 1. Skew 2. Split 2

Have a Question? sli. do #Ds. Algo 3

AVL Trees Properties and Rotations

AVL Tree § AVL tree is a self-balancing binary-search tree (visualization) § Height of two subtrees can differ by at most 1 17 9 5 25 12 Average Space O(n) Search O(log n) Insert O(log n) Worst case O(n) O(log n) Delete O(log n) 5

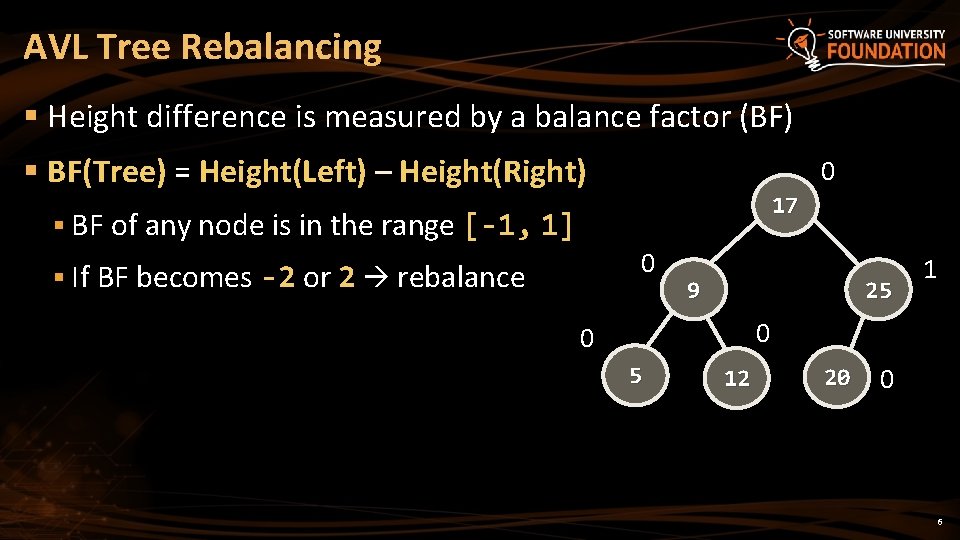
AVL Tree Rebalancing § Height difference is measured by a balance factor (BF) § BF(Tree) = Height(Left) – Height(Right) 0 17 § BF of any node is in the range [-1, 1] 0 § If BF becomes -2 or 2 rebalance 9 25 1 0 0 5 12 20 0 6

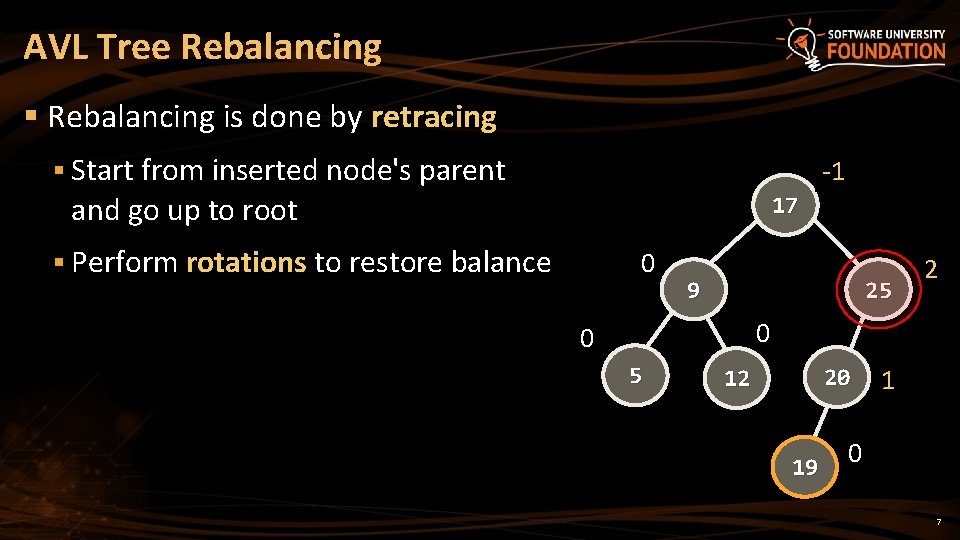
AVL Tree Rebalancing § Rebalancing is done by retracing § Start from inserted node's parent 0 -1 and go up to root 17 § Perform rotations to restore balance 0 9 25 12 0 0 5 20 12 19 01 0 7

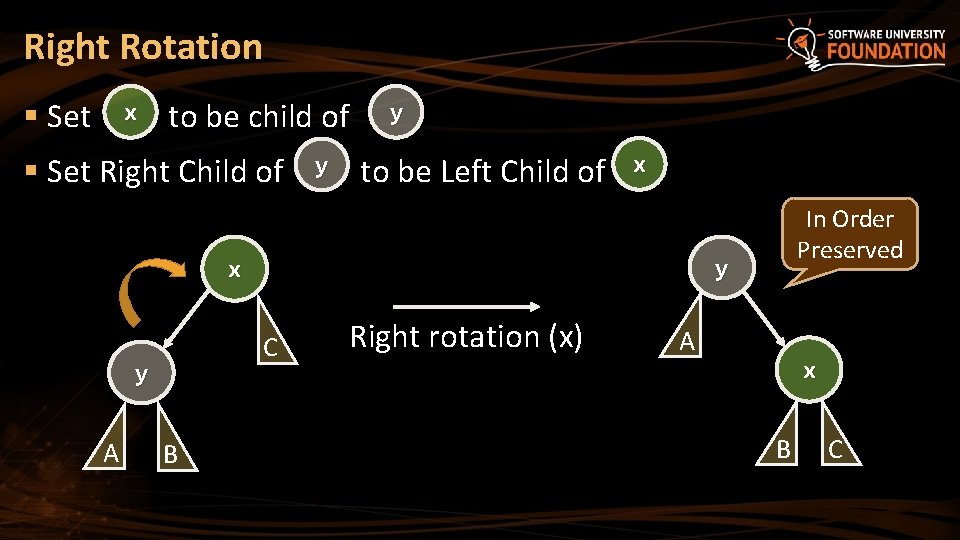
Right Rotation § Set x to be child of § Set Right Child of y y to be Left Child of x y x C y A B In Order Preserved Right rotation (x) A x B C

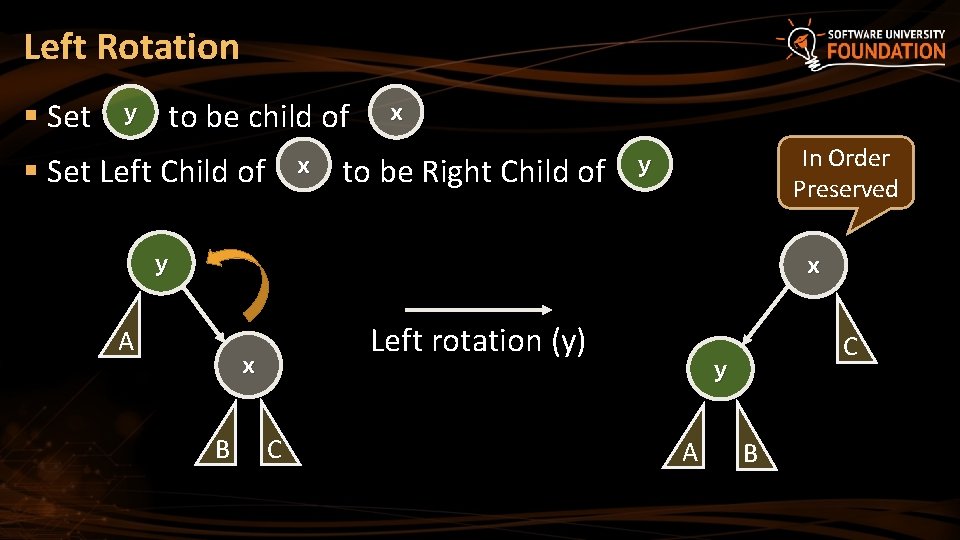
Left Rotation § Set y to be child of § Set Left Child of x x to be Right Child of In Order Preserved y y x A Left rotation (y) x B C C y A B

AVL Tree Insertion Algorithm 1. Insert like in ordinary BST 4 2. Retrace up to root 1. Modify balance / height 2. If balance factor ∉ [-1, 1] rebalance 20 3 2 12 2 2 8 1 17 1 1 1 4 25 10 1 15 26 19 10

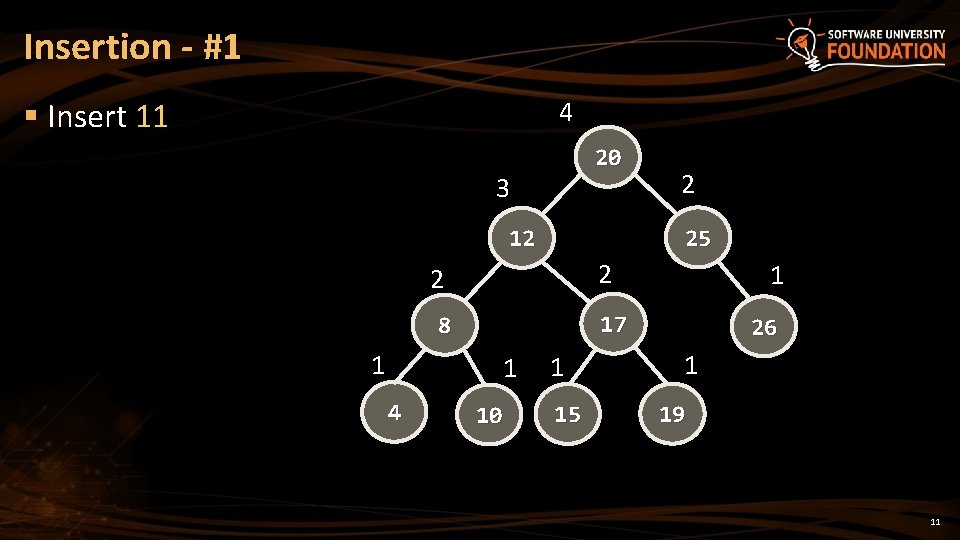
Insertion - #1 § Insert 11 4 20 3 25 12 2 2 1 4 1 17 8 1 2 10 1 15 26 1 19 11

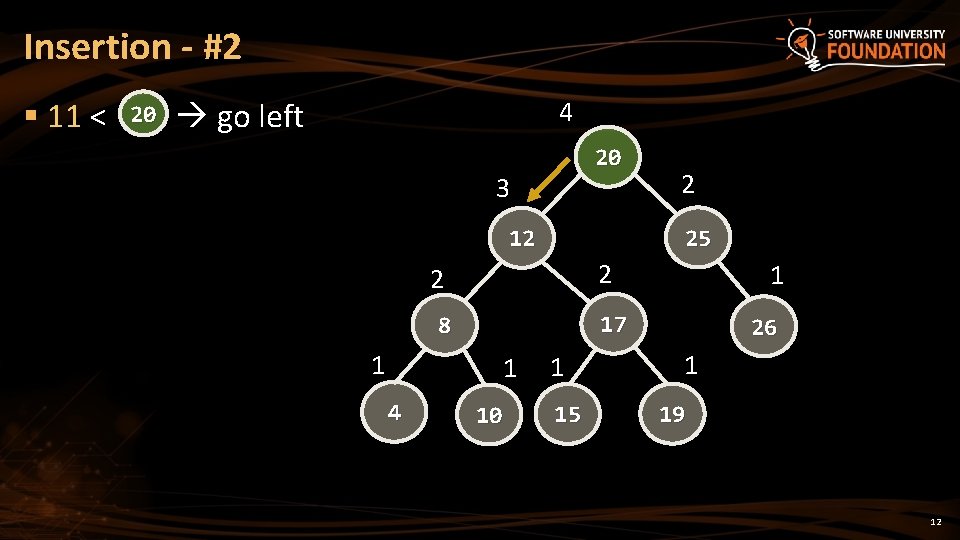
Insertion - #2 § 11 < 20 go left 4 20 3 25 12 2 2 1 4 1 17 8 1 2 10 1 15 26 1 19 12

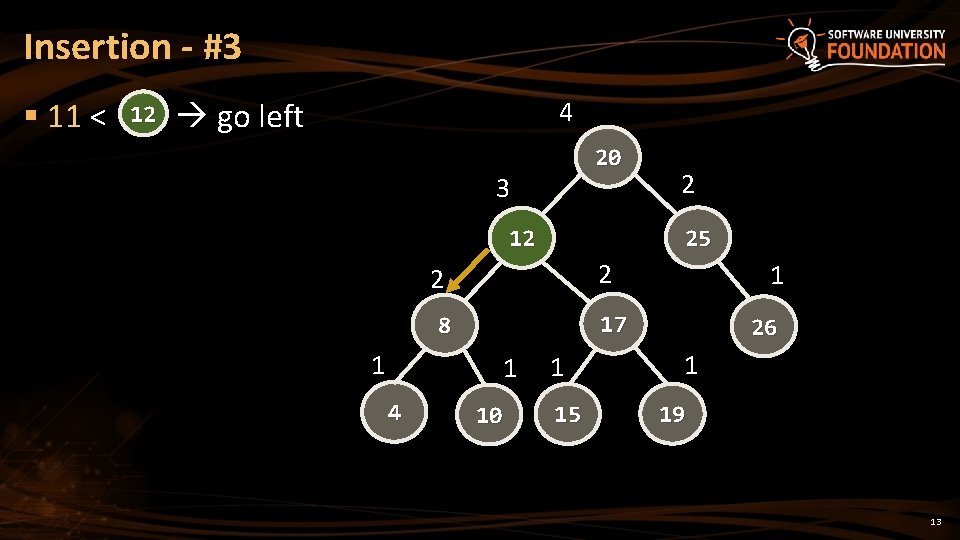
Insertion - #3 § 11 < 12 go left 4 20 3 25 12 2 2 1 4 1 17 8 1 2 10 1 15 26 1 19 13

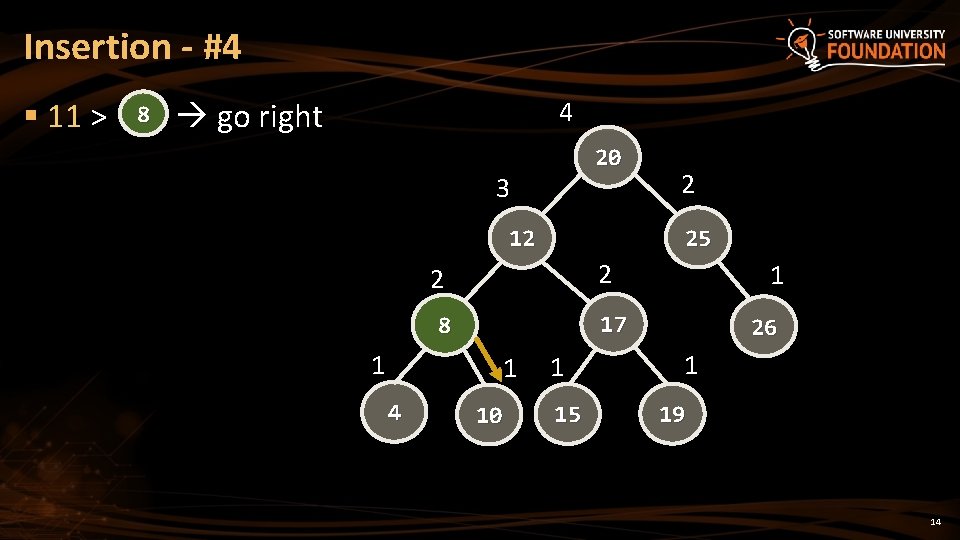
Insertion - #4 § 11 > 8 go right 4 20 3 25 12 2 2 1 4 1 17 8 1 2 10 1 15 26 1 19 14

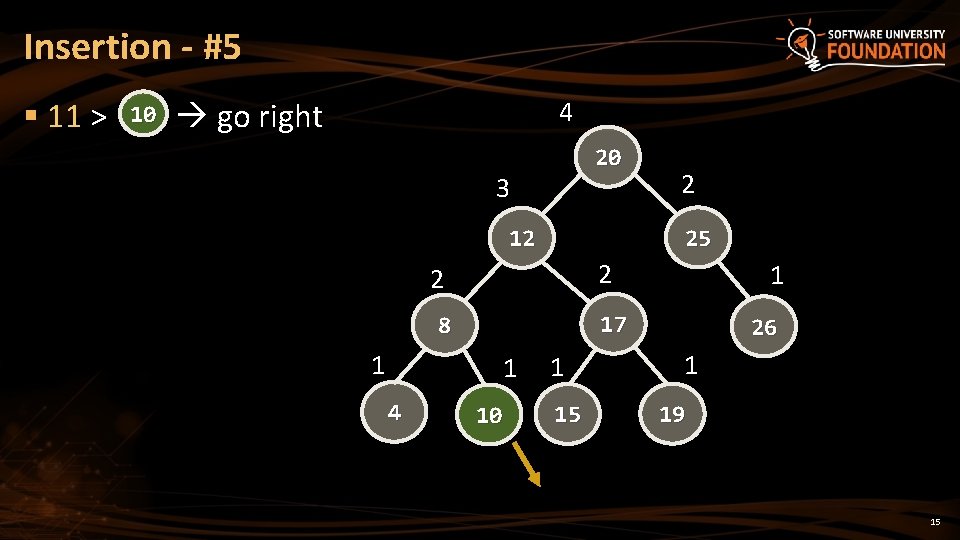
Insertion - #5 § 11 > 10 go right 4 20 3 25 12 2 2 1 4 1 17 8 1 2 10 1 15 26 1 19 15

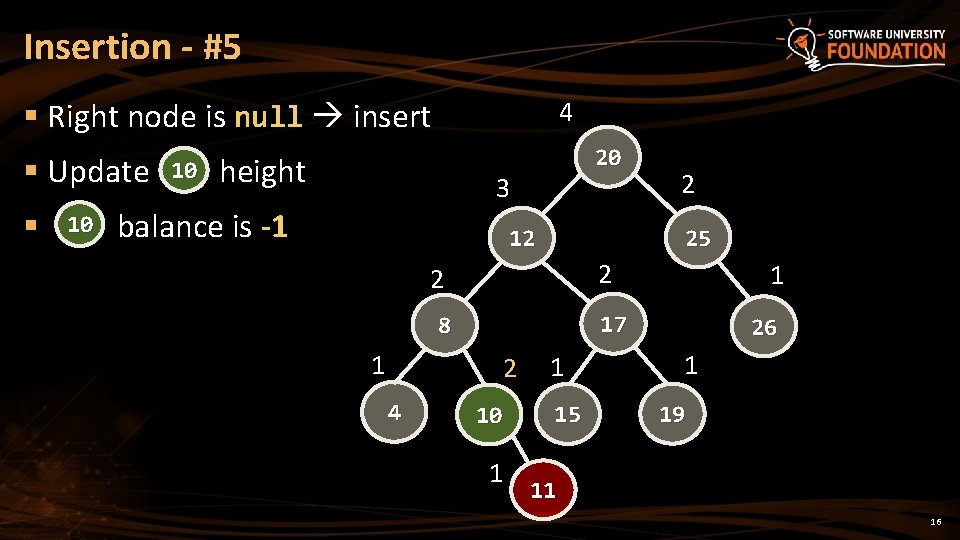
Insertion - #5 § Right node is null insert § Update § 10 10 4 height 20 3 balance is -1 25 12 2 4 1 17 8 1 2 10 1 1 15 26 1 19 11 16

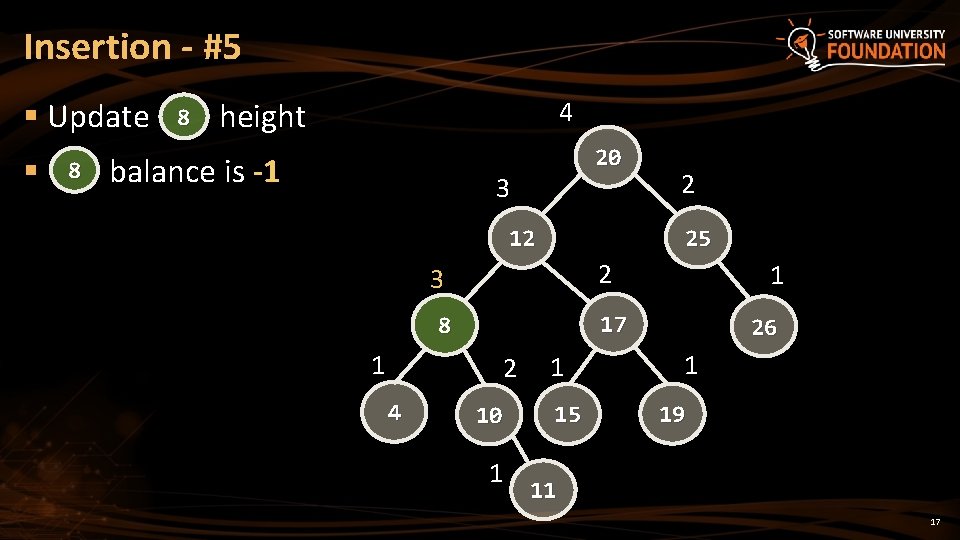
Insertion - #5 § Update § 8 8 height 4 balance is -1 20 3 25 12 2 3 2 4 1 17 8 1 2 10 1 1 15 26 1 19 11 17

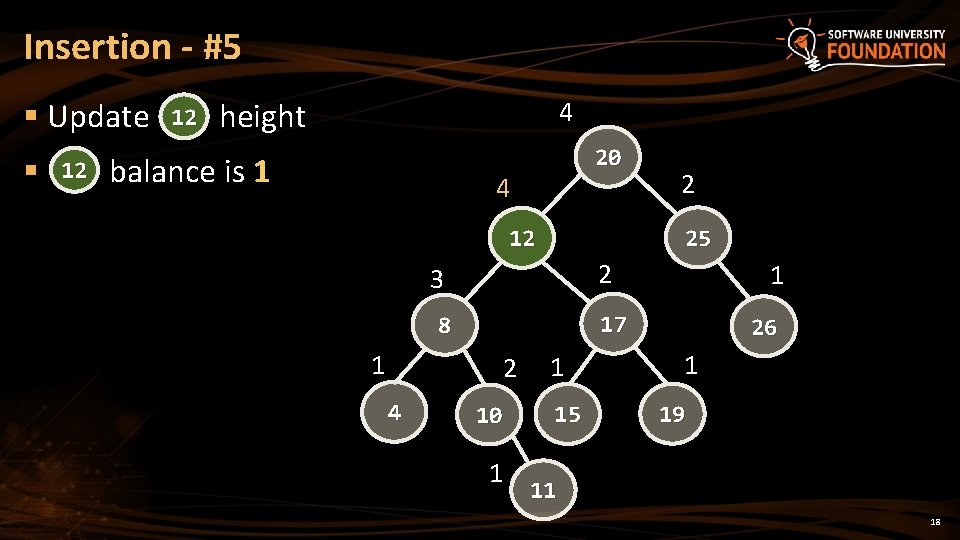
Insertion - #5 § Update § 12 12 height 4 balance is 1 20 4 25 12 2 3 2 4 1 17 8 1 2 10 1 1 15 26 1 19 11 18

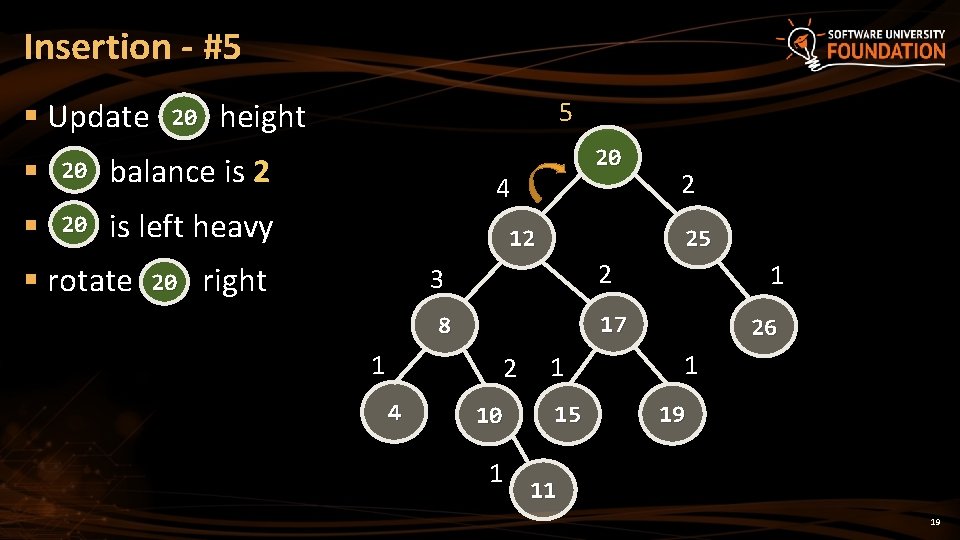
Insertion - #5 § Update 20 height § 20 balance is 2 § 20 is left heavy § rotate 20 5 20 4 25 12 right 2 3 2 4 1 17 8 1 2 10 1 1 15 26 1 19 11 19

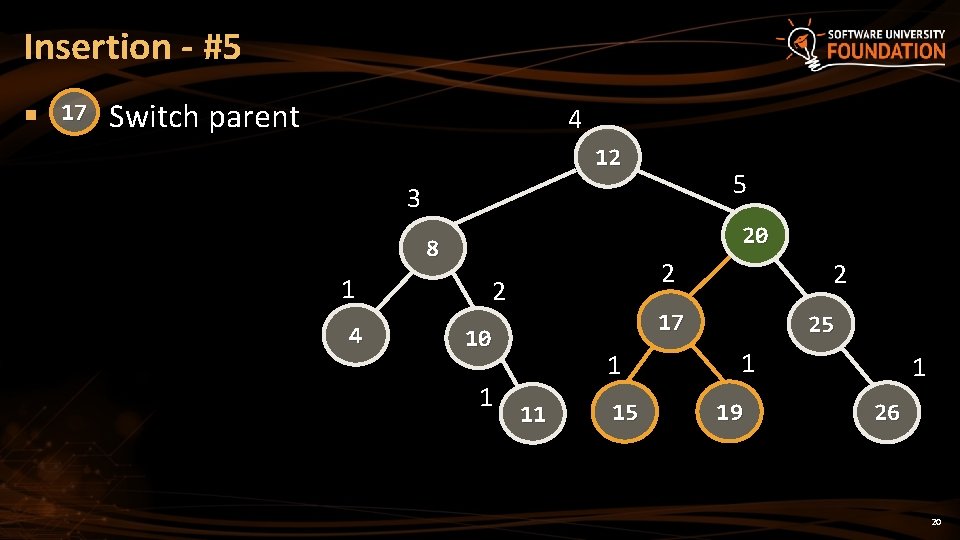
Insertion - #5 § 17 Switch parent 4 12 5 3 20 8 1 4 2 2 17 10 1 2 1 11 15 25 1 19 1 26 20

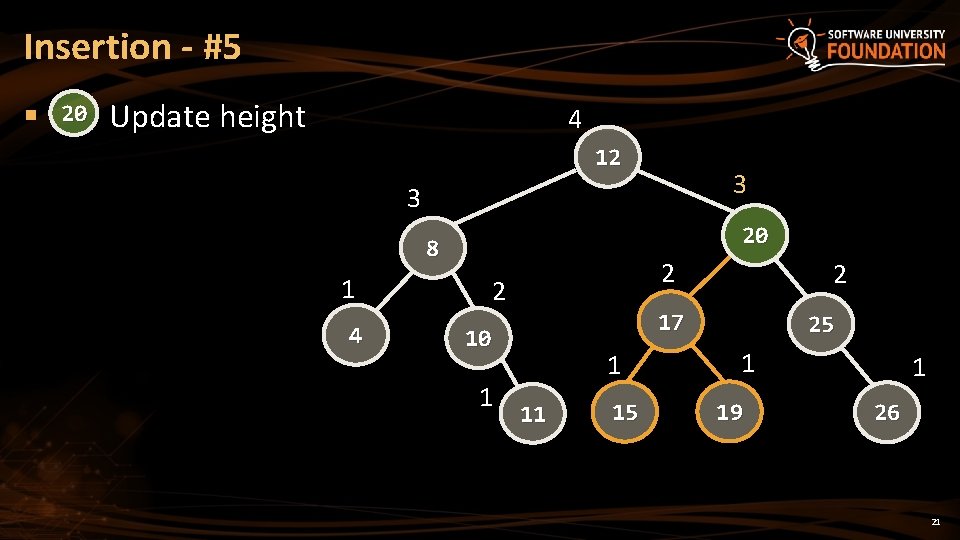
Insertion - #5 § 20 Update height 4 12 3 3 20 8 1 4 2 2 17 10 1 2 1 11 15 25 1 19 1 26 21

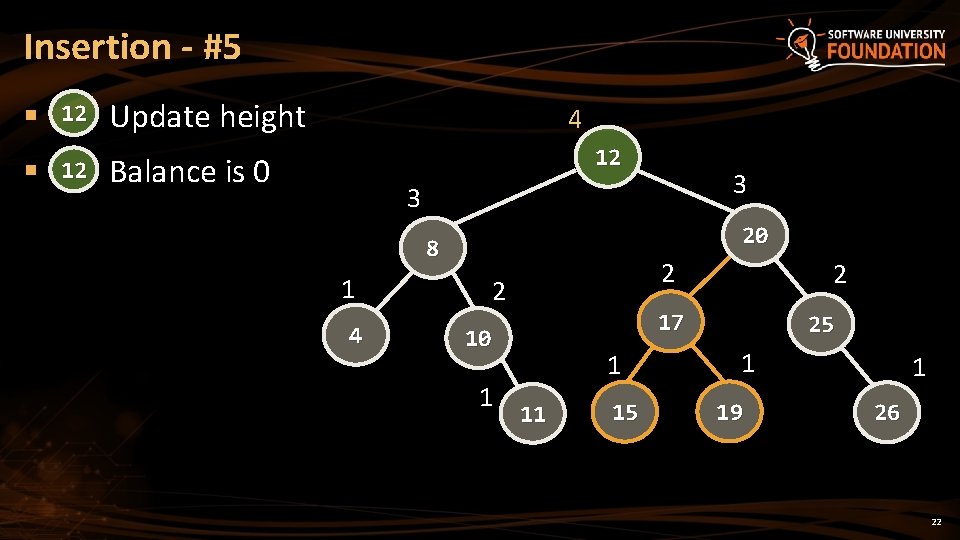
Insertion - #5 § 12 Update height 4 12 Balance is 0 3 3 20 8 1 4 2 2 17 10 1 2 1 11 15 25 1 19 1 26 22

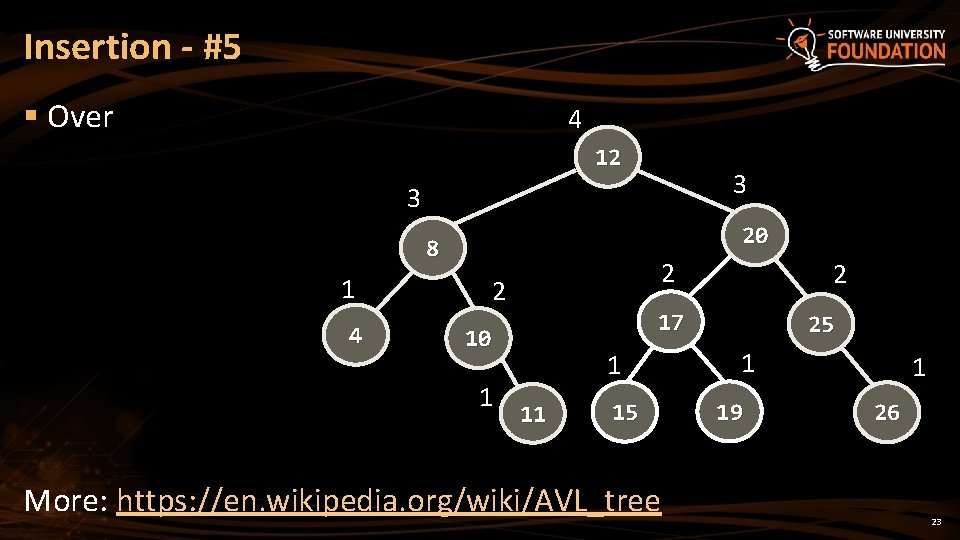
Insertion - #5 § Over 4 12 3 3 20 8 1 4 2 2 17 10 1 2 1 11 15 More: https: //en. wikipedia. org/wiki/AVL_tree 25 1 19 1 26 23

AVL Tree - Quiz TIME’S UP! TIME: § Delete 25. What will be the resulting tree? 17 9 5 25 12 24

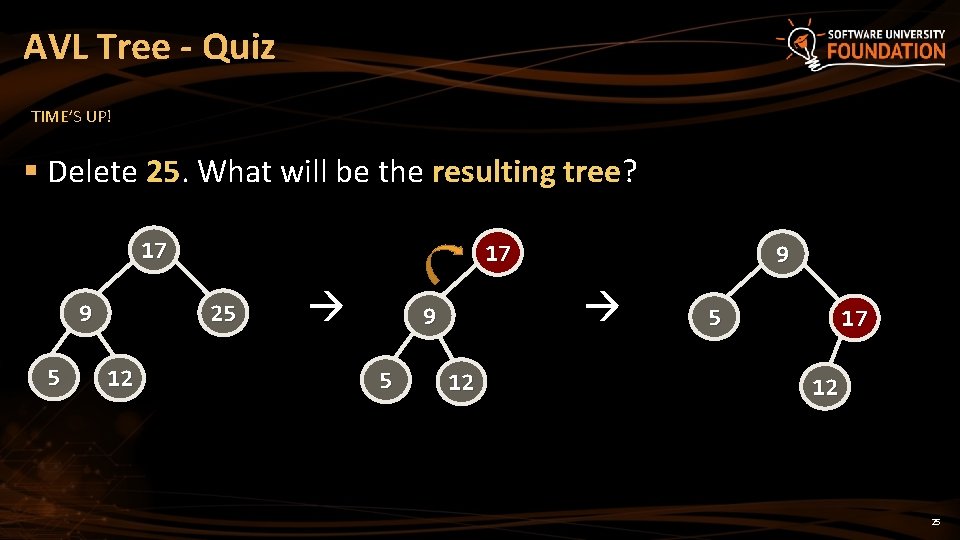
AVL Tree - Quiz TIME’S UP! § Delete 25. What will be the resulting tree? 17 9 5 17 25 12 9 5 9 12 5 17 12 25

Double Rotations Double Left, Double Right Rotation

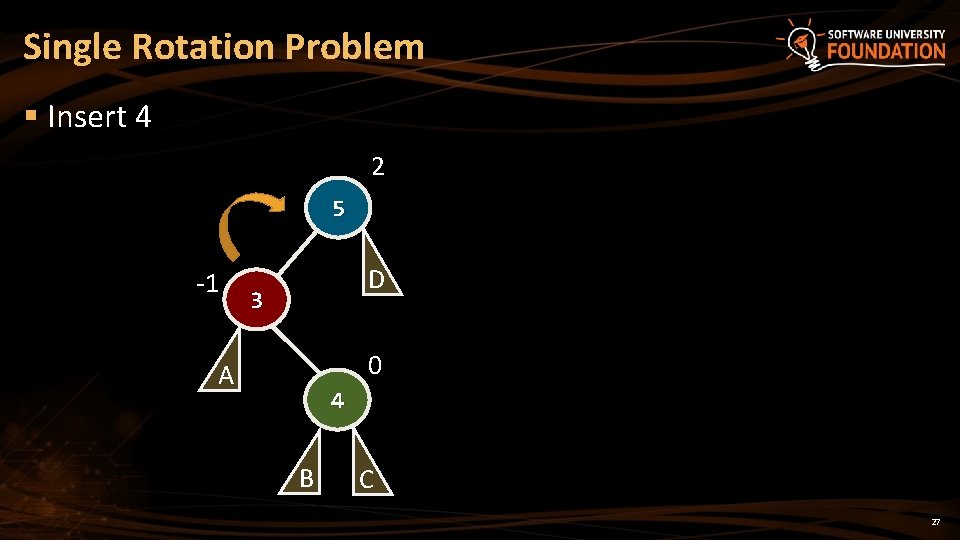
Single Rotation Problem § Insert 4 2 5 -1 D 3 0 A 4 B C 27

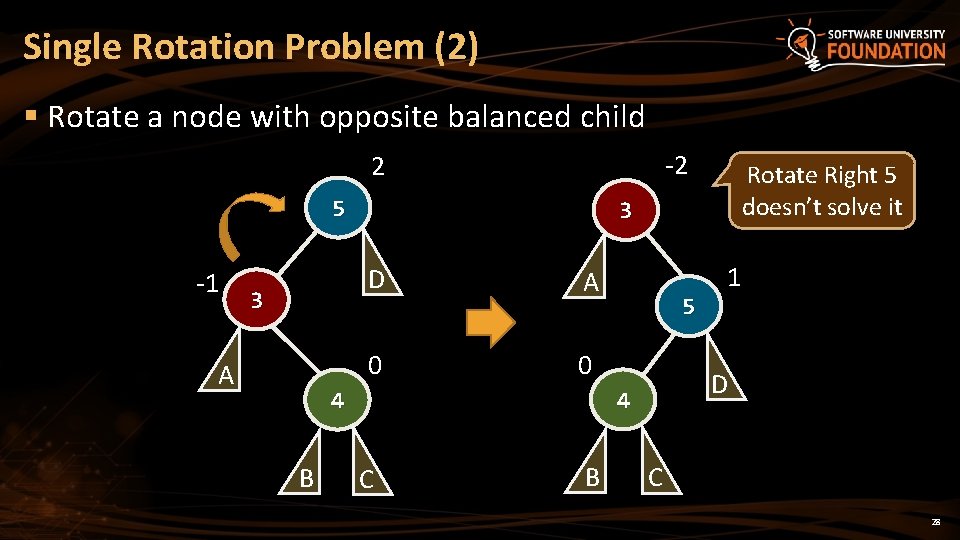
Single Rotation Problem (2) § Rotate a node with opposite balanced child -2 2 5 -1 3 A 3 D A 0 0 5 C B 1 D 4 4 B Rotate Right 5 doesn’t solve it C 28

Double Right Rotation Right-Left

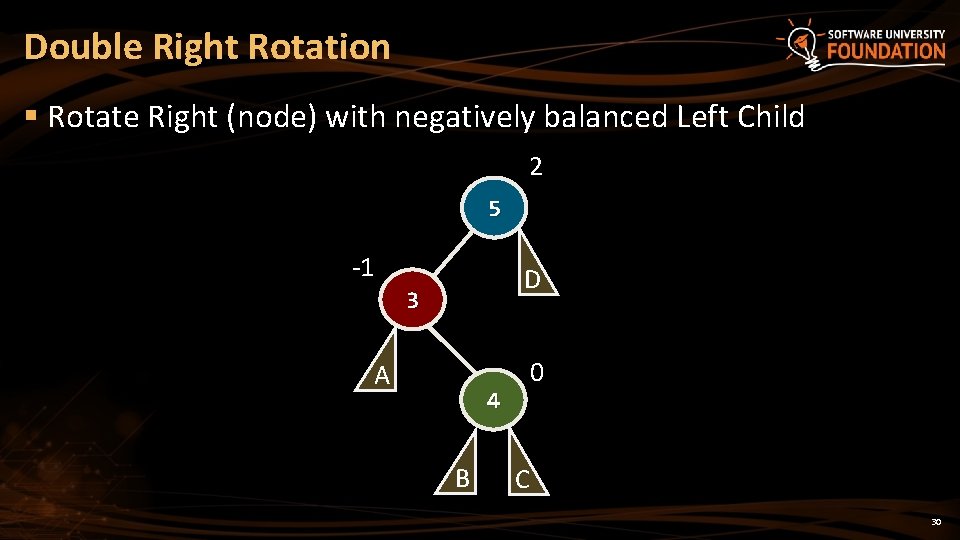
Double Right Rotation § Rotate Right (node) with negatively balanced Left Child 2 5 -1 D 3 A 0 4 B C 30

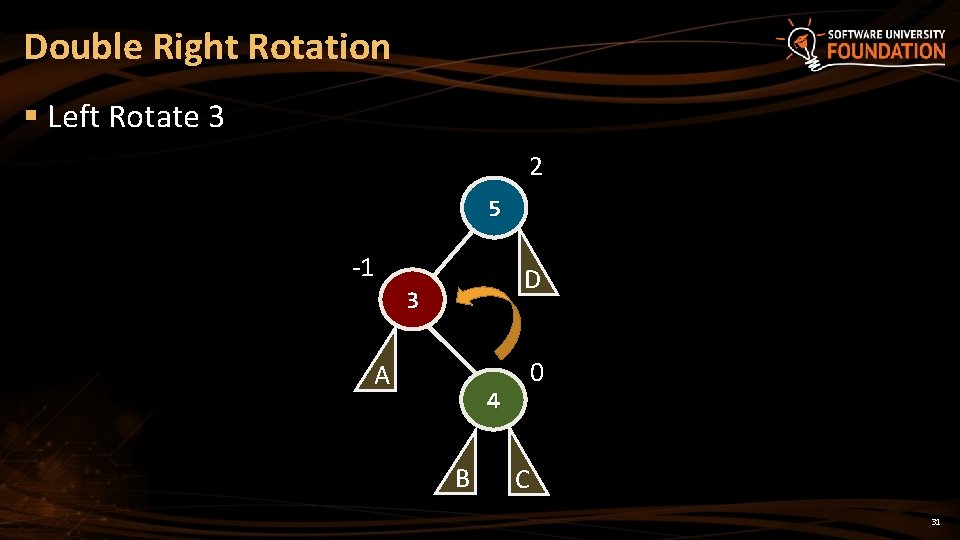
Double Right Rotation § Left Rotate 3 2 5 -1 D 3 A 0 4 B C 31

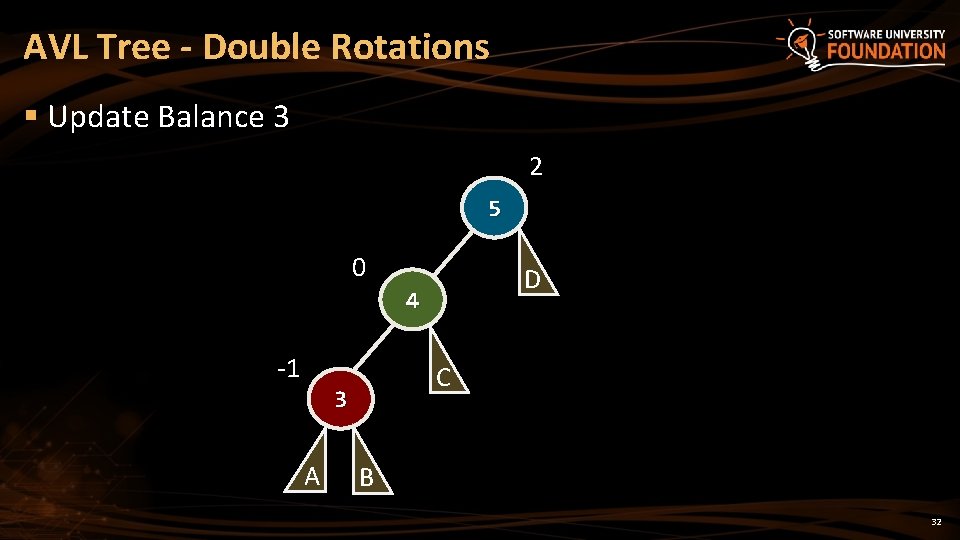
AVL Tree - Double Rotations § Update Balance 3 2 5 0 D 4 -1 C 3 A B 32

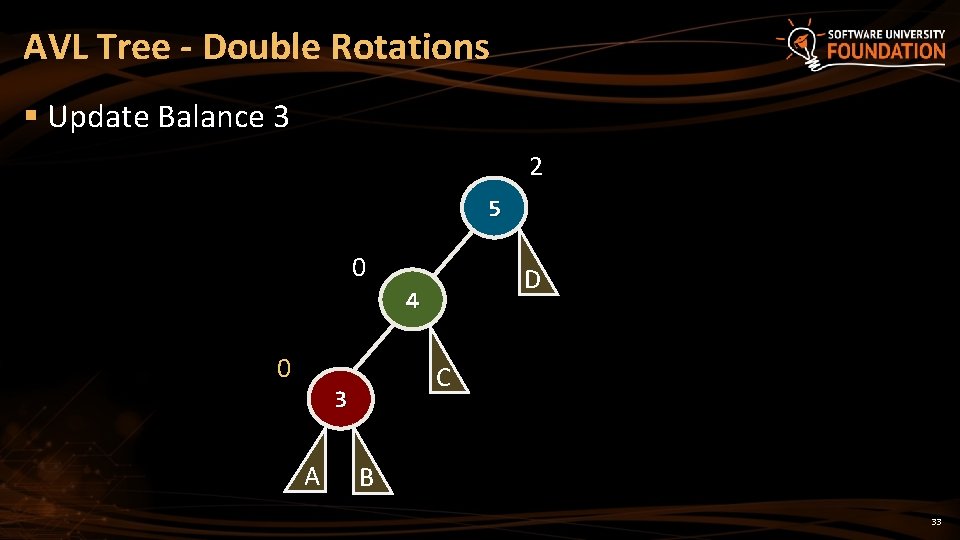
AVL Tree - Double Rotations § Update Balance 3 2 5 0 D 4 0 C 3 A B 33

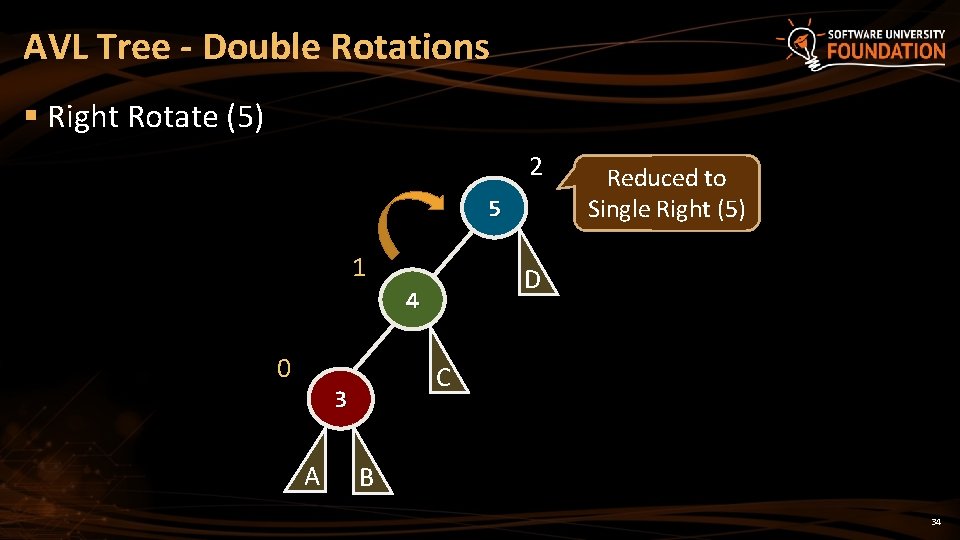
AVL Tree - Double Rotations § Right Rotate (5) 2 5 1 D 4 0 C 3 A Reduced to Single Right (5) B 34

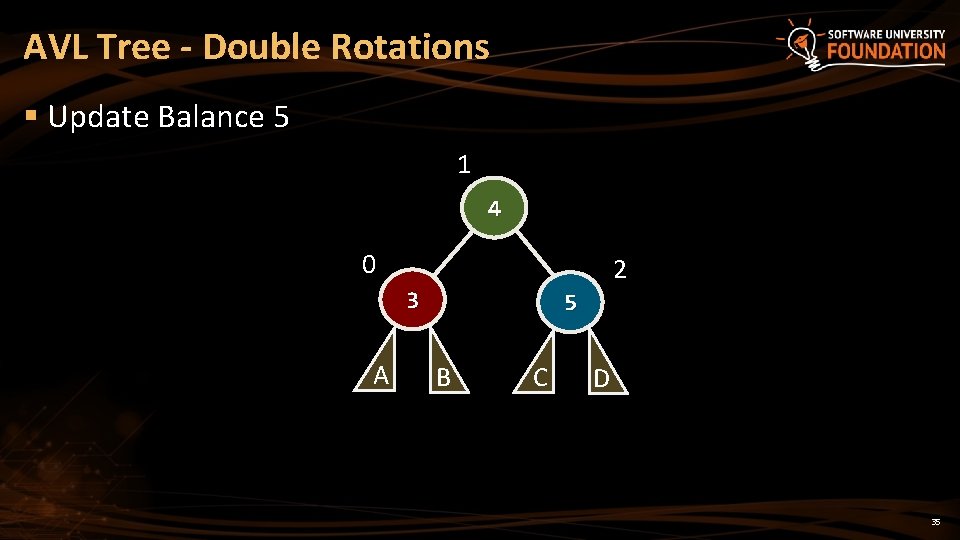
AVL Tree - Double Rotations § Update Balance 5 1 4 0 2 3 A 5 B C D 35

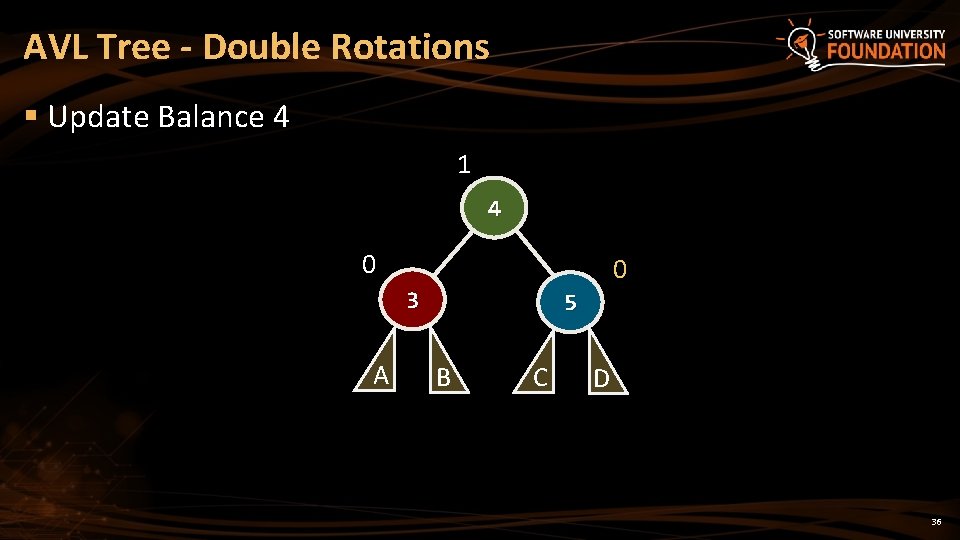
AVL Tree - Double Rotations § Update Balance 4 1 4 0 0 3 A 5 B C D 36

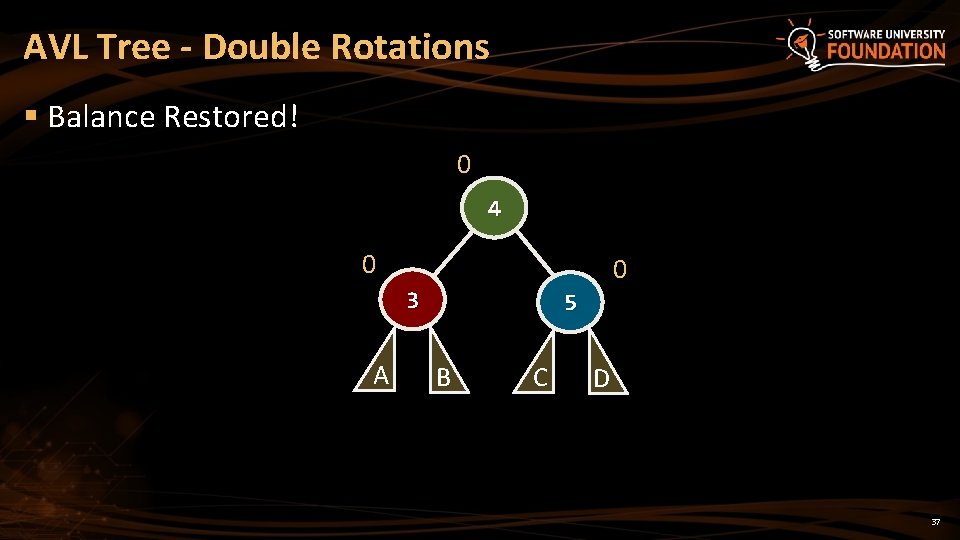
AVL Tree - Double Rotations § Balance Restored! 0 4 0 0 3 A 5 B C D 37

Double Left Rotation Left-Right

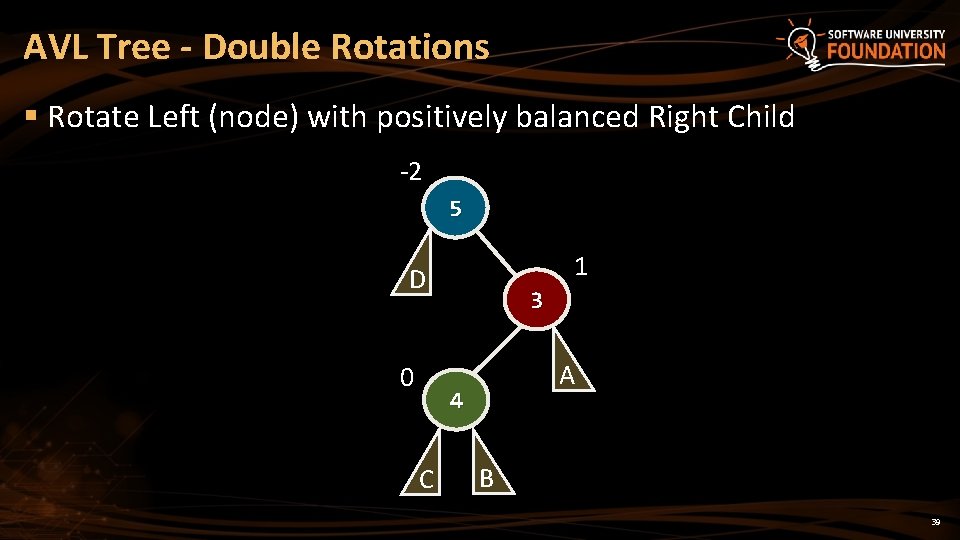
AVL Tree - Double Rotations § Rotate Left (node) with positively balanced Right Child -2 5 1 D 0 3 A 4 C B 39

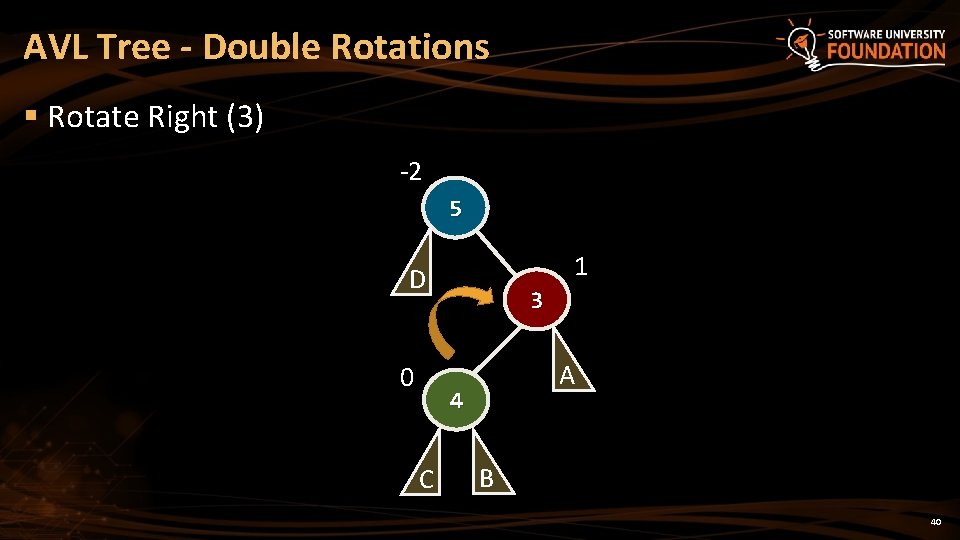
AVL Tree - Double Rotations § Rotate Right (3) -2 5 1 D 0 3 A 4 C B 40

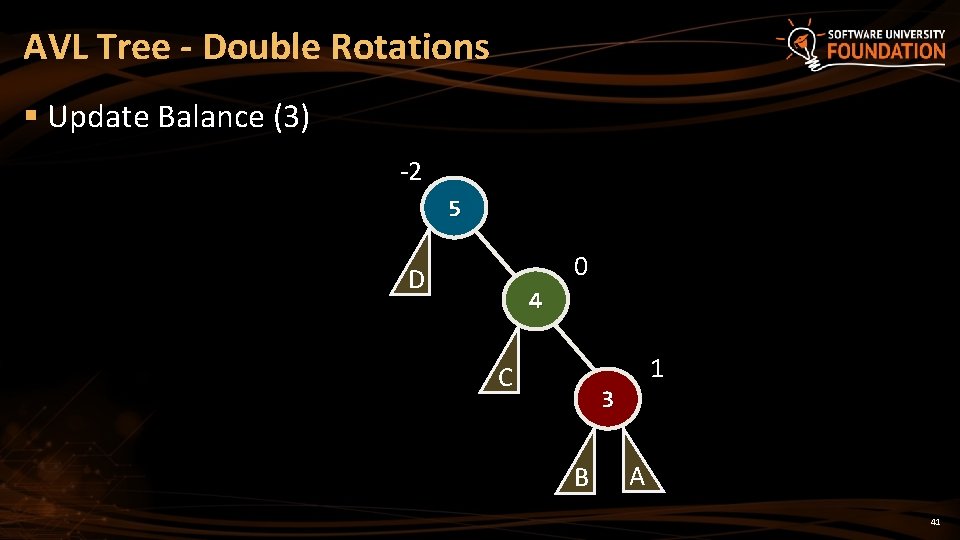
AVL Tree - Double Rotations § Update Balance (3) -2 5 0 D 4 1 C 3 B A 41

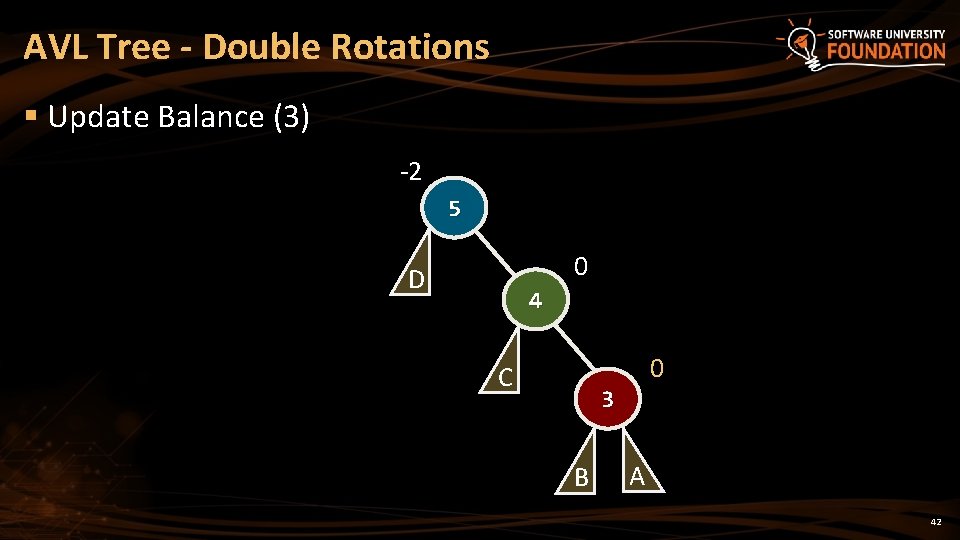
AVL Tree - Double Rotations § Update Balance (3) -2 5 0 D 4 0 C 3 B A 42

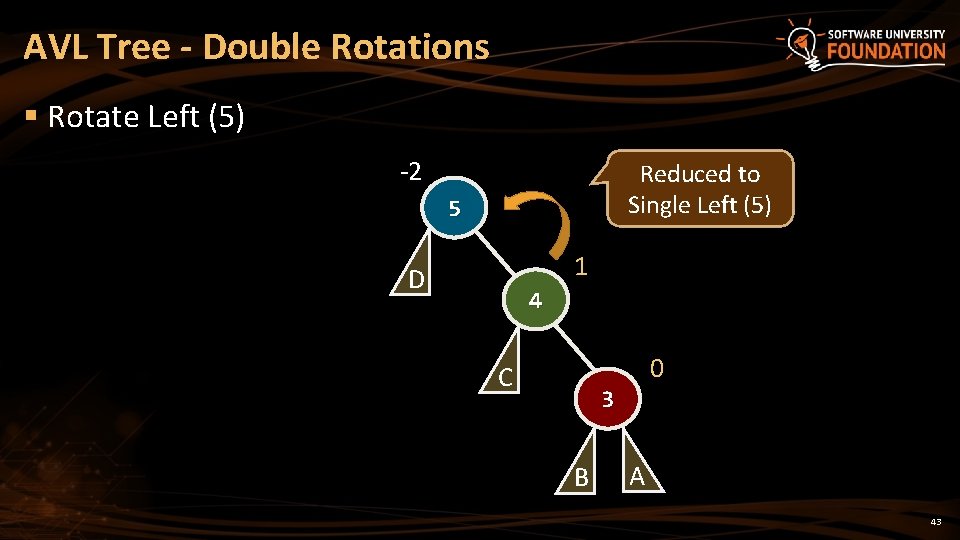
AVL Tree - Double Rotations § Rotate Left (5) -2 Reduced to Single Left (5) 5 1 D 4 0 C 3 B A 43

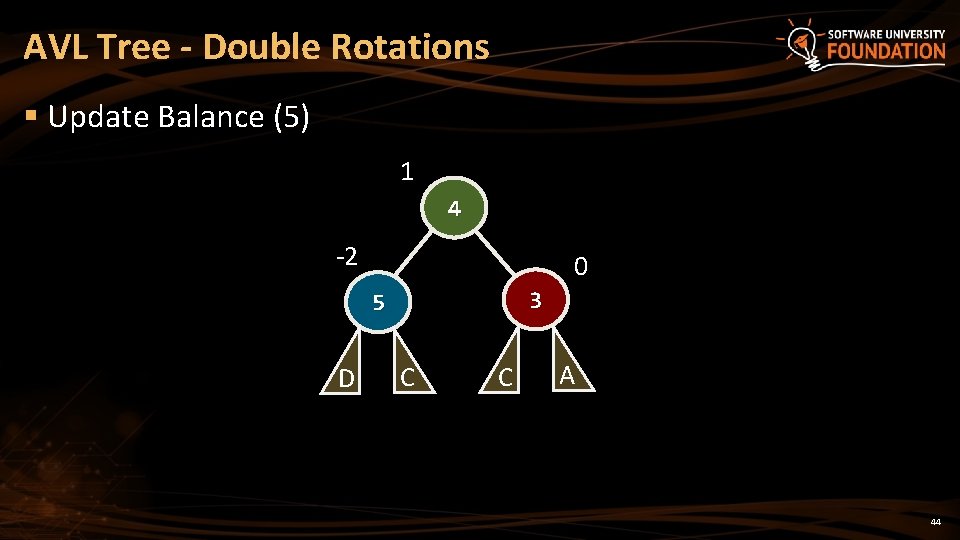
AVL Tree - Double Rotations § Update Balance (5) 1 4 -2 0 3 5 D C C A 44

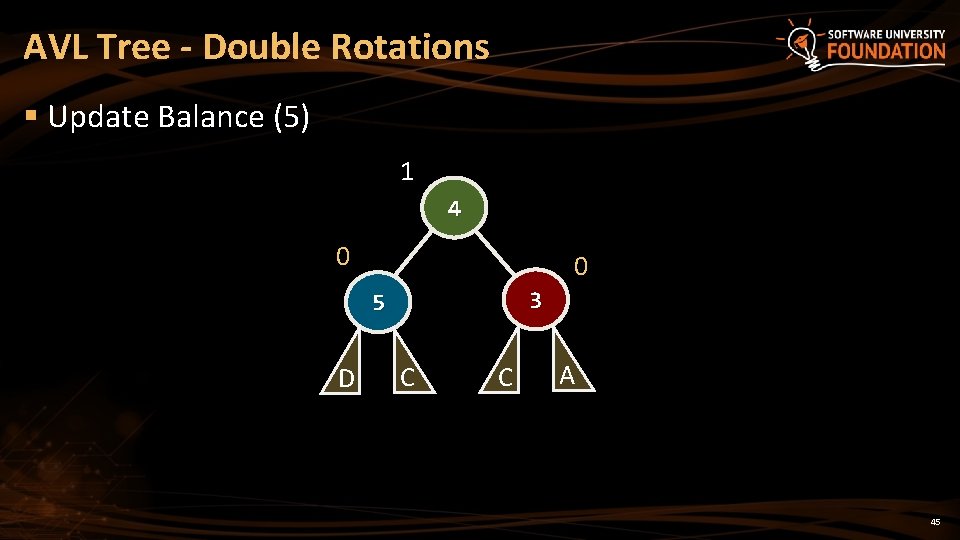
AVL Tree - Double Rotations § Update Balance (5) 1 4 0 0 3 5 D C C A 45

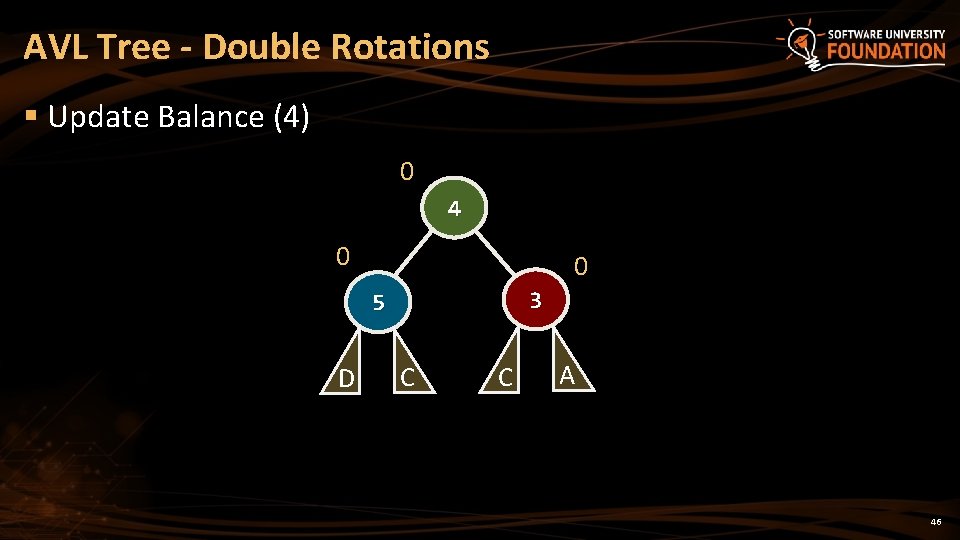
AVL Tree - Double Rotations § Update Balance (4) 0 4 0 0 3 5 D C C A 46

AVL Tree - Quiz TIME’S UP! TIME: § Insert 22. What will be the resulting tree? 17 9 5 25 12 20 47

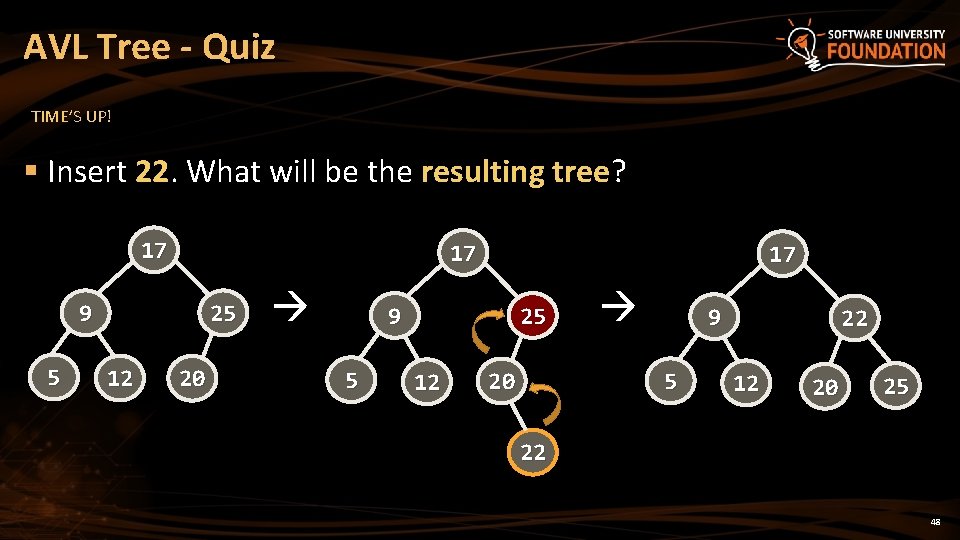
AVL Tree - Quiz TIME’S UP! § Insert 22. What will be the resulting tree? 17 17 9 5 25 12 20 17 9 5 25 12 9 5 20 22 12 20 25 22 48

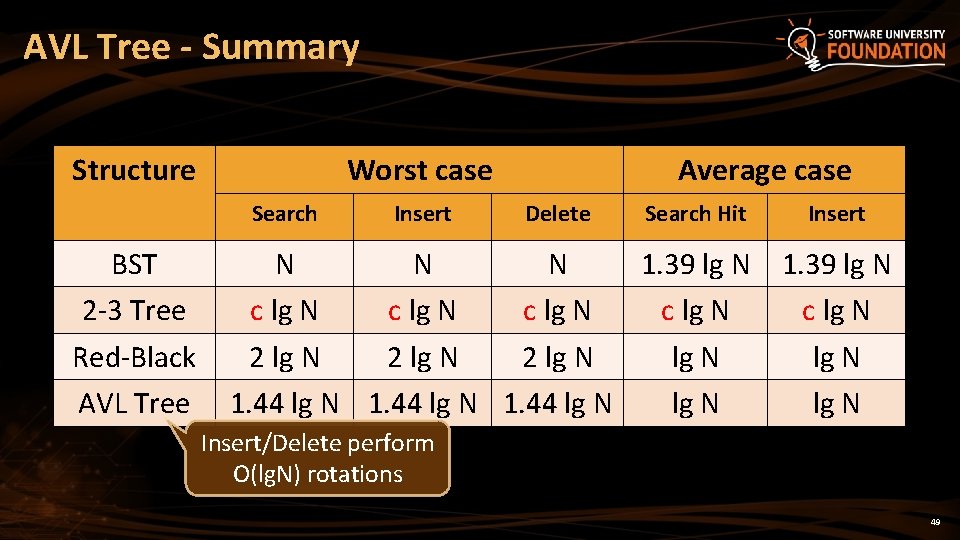
AVL Tree - Summary Structure Worst case Search BST 2 -3 Tree Red-Black AVL Tree Insert Average case Delete Search Hit Insert N N N 1. 39 lg N c lg N c lg N 2 lg N 1. 44 lg N lg N Insert/Delete perform O(lg. N) rotations 49

17 9 5 25 12 20 22 AVL Tree Balancing Implementation 50

Rotate Right public static Node<T> Rotate. Right(Node<T> node) { Node<T> left = node. Left; node. Left = node. Left. Right; left. Right = node; Update. Height(node); } return left; 51

Balance Node private static Node<T> Balance(Node<T> node) { int balance = Height(node. Left) - Height(node. Right); if (balance < -1) // Right child is heavy { balance = Height(node. Right. Left) - Height(node. Right); if (balance <= 0) { return Rotate. Left(node); } else { node. Right = Rotate. Right(node. Right); return Rotate. Left(node); } } else if (balance > 1) // Left child is heavy { balance = Height(node. Left) - Height(node. Left. Right); if (balance >= 0) { return Rotate. Right(node); } else { node. Left = Rotate. Left(node. Left); return Rotate. Right(node); } } } return node; 52

Lab Exercise AVL Tree - Balancing

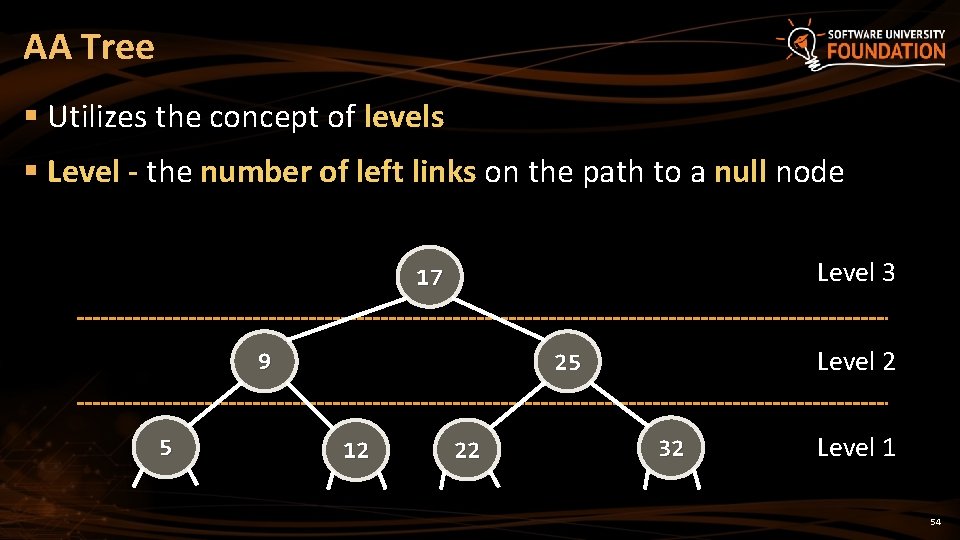
AA Tree § Utilizes the concept of levels § Level - the number of left links on the path to a null node Level 3 17 9 5 Level 2 25 12 22 32 Level 1 54

AA Tree § AA tree invariants § The level of every leaf node is one § Every left child has level one less than its parent § Every right child has level equal to or one less than its parent § Right grandchildren have levels less than their grandparents § Every node of level greater than one has two children 55

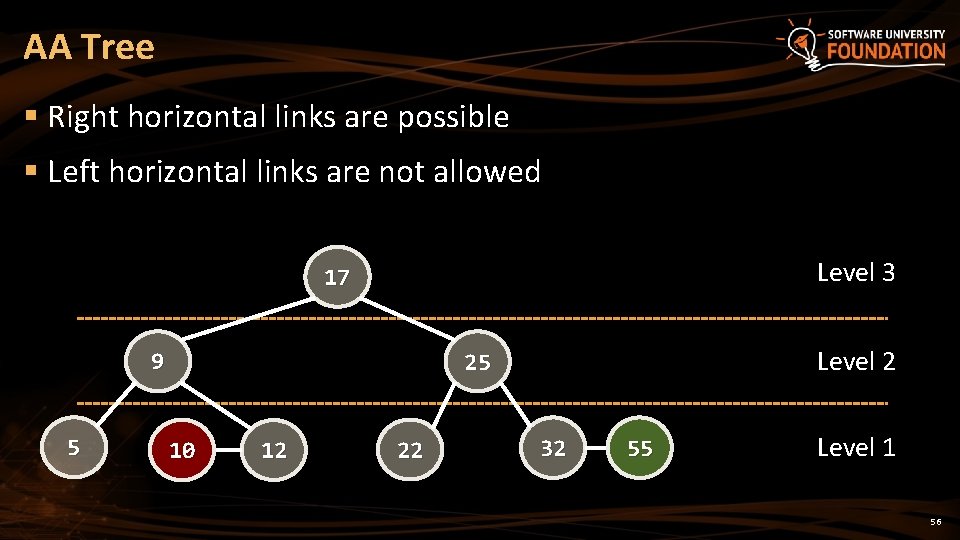
AA Tree § Right horizontal links are possible § Left horizontal links are not allowed Level 3 17 9 5 Level 2 25 10 12 22 32 55 Level 1 56

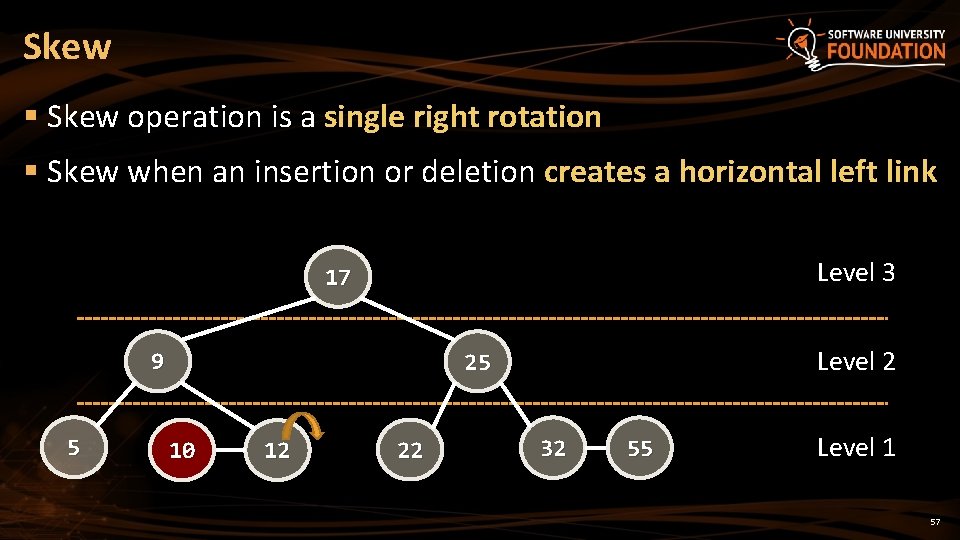
Skew § Skew operation is a single right rotation § Skew when an insertion or deletion creates a horizontal left link Level 3 17 9 5 Level 2 25 10 12 22 32 55 Level 1 57

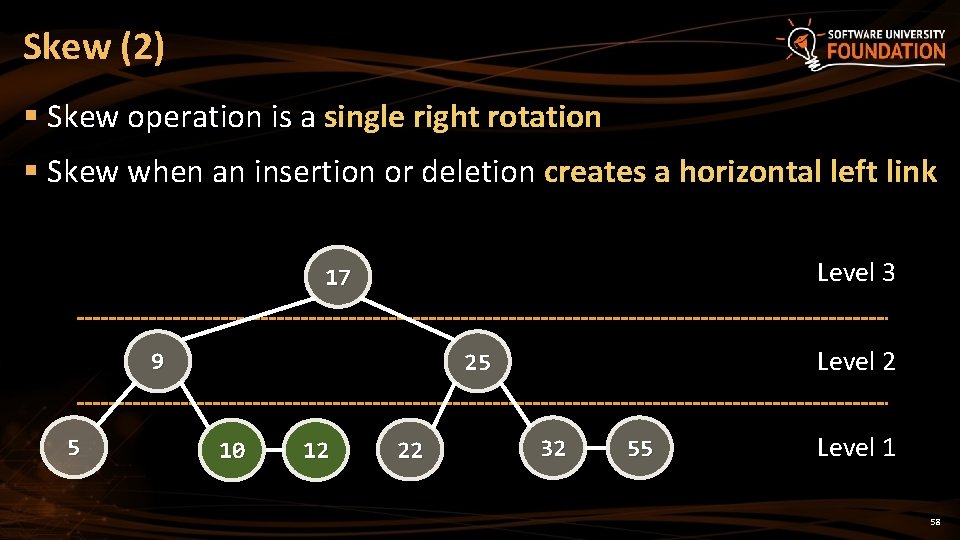
Skew (2) § Skew operation is a single right rotation § Skew when an insertion or deletion creates a horizontal left link Level 3 17 9 5 Level 2 25 10 12 22 32 55 Level 1 58

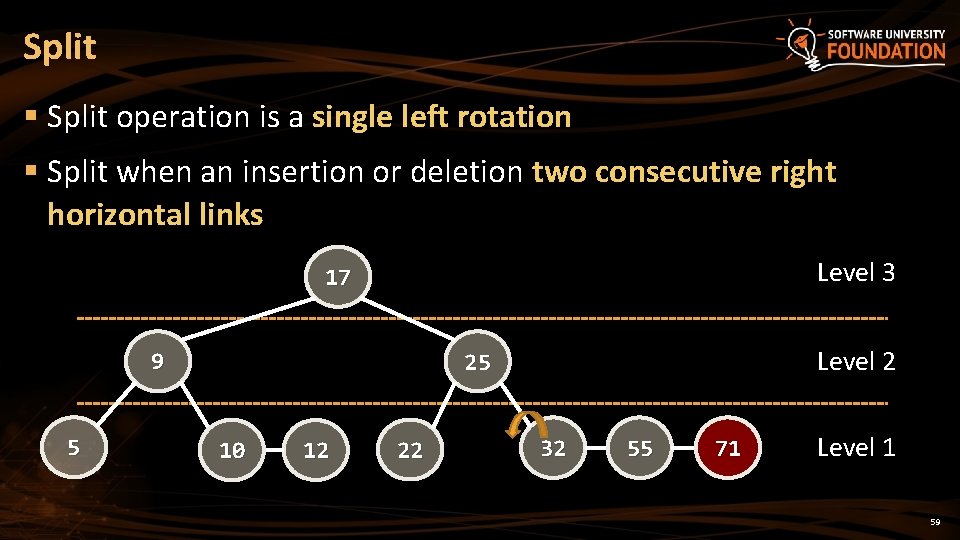
Split § Split operation is a single left rotation § Split when an insertion or deletion two consecutive right horizontal links Level 3 17 9 5 Level 2 25 10 12 22 32 55 71 Level 1 59

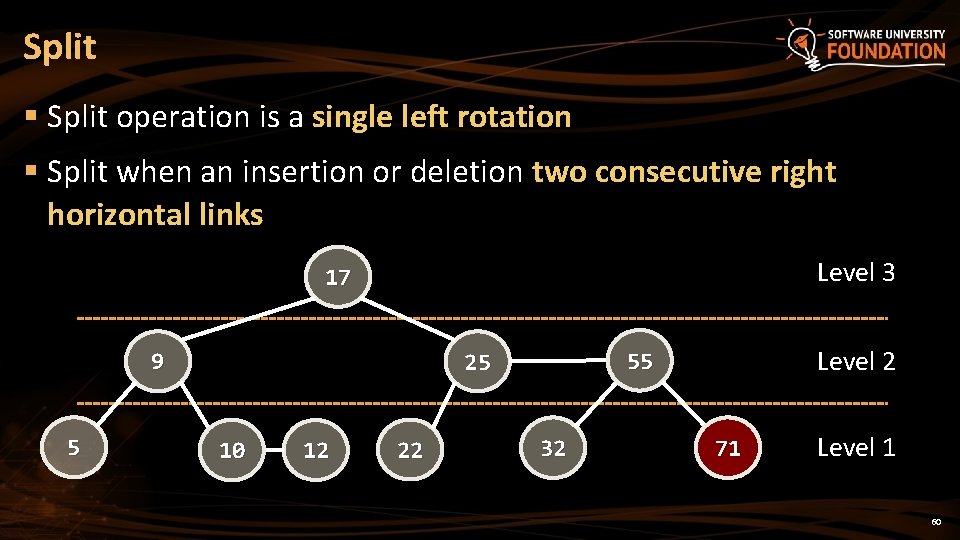
Split § Split operation is a single left rotation § Split when an insertion or deletion two consecutive right horizontal links Level 3 17 9 5 10 12 22 Level 2 55 25 32 71 Level 1 60

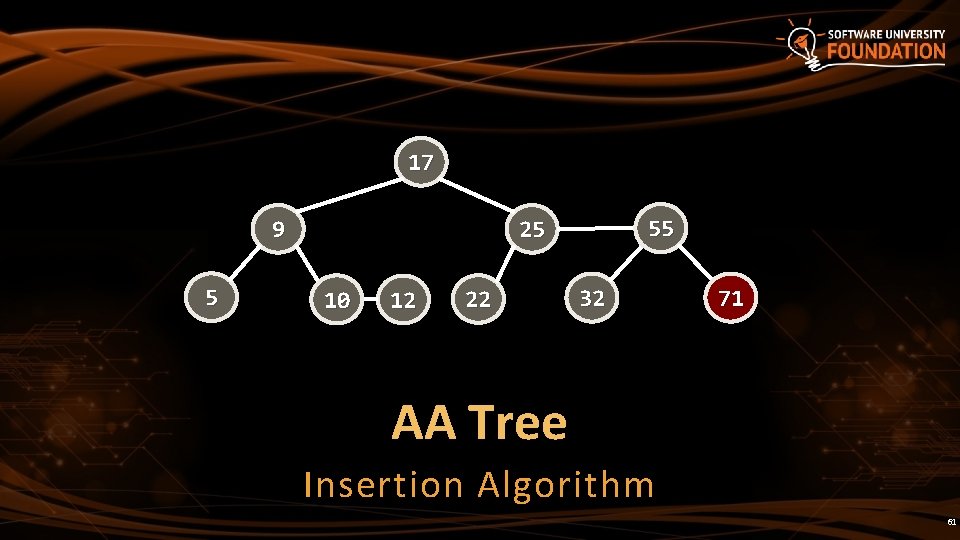
17 9 5 55 25 10 12 22 32 71 AA Tree Insertion Algorithm 61

AA Tree Insertion #1 § Insert: 6 § New nodes are always inserted at Level 1 Level 3 Level 2 6 Level 1 62

AA Tree Insertion #1 § Insert: 2 Level 3 Level 2 6 Level 1 63

AA Tree Insertion #1 § Left horizontal link is not allowed § Rotate 6 right (skew) Level 3 Level 2 2 6 Level 1 64

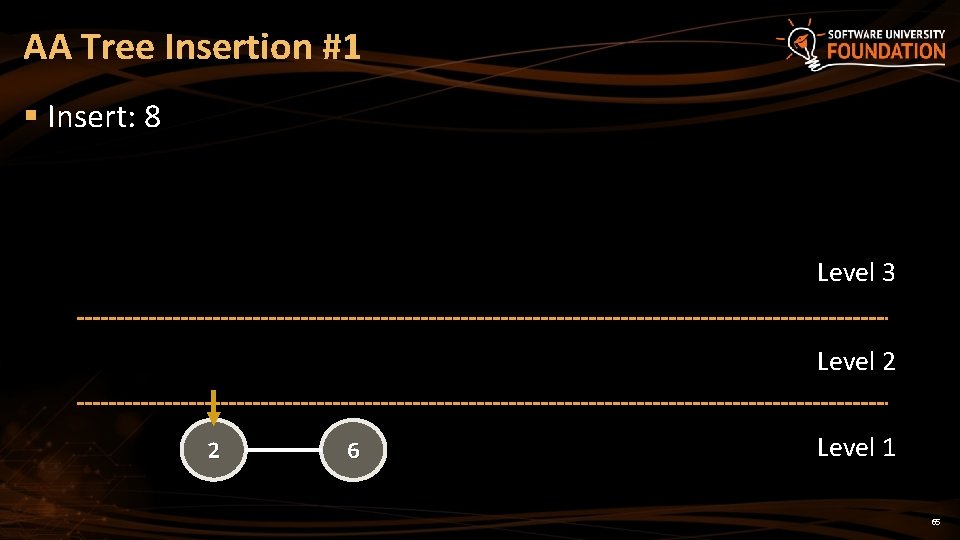
AA Tree Insertion #1 § Insert: 8 Level 3 Level 2 2 6 Level 1 65

AA Tree Insertion #1 § Insert: 8 Level 3 Level 2 2 6 Level 1 66

AA Tree Insertion #1 § Insert: 8 Level 3 Level 2 2 6 Level 1 67

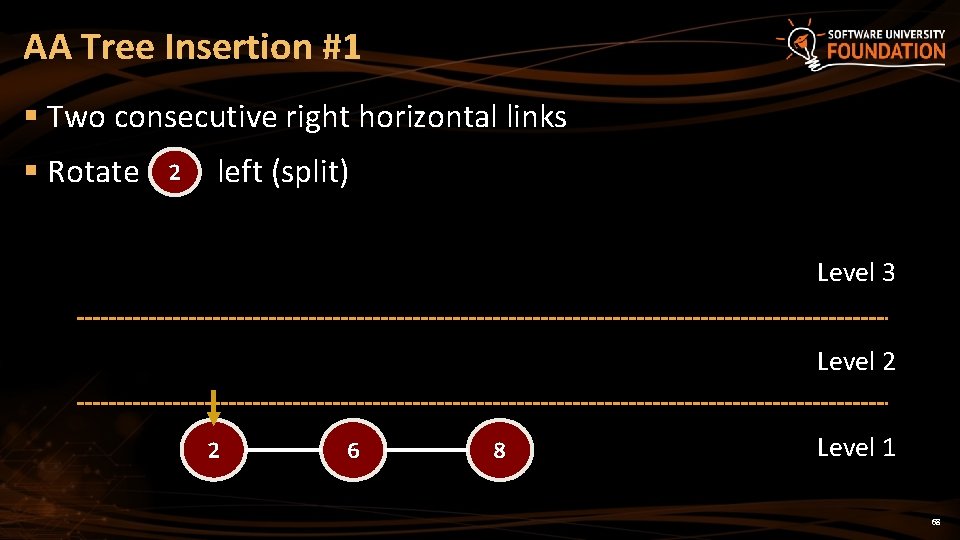
AA Tree Insertion #1 § Two consecutive right horizontal links § Rotate 2 left (split) Level 3 Level 2 2 6 8 Level 1 68

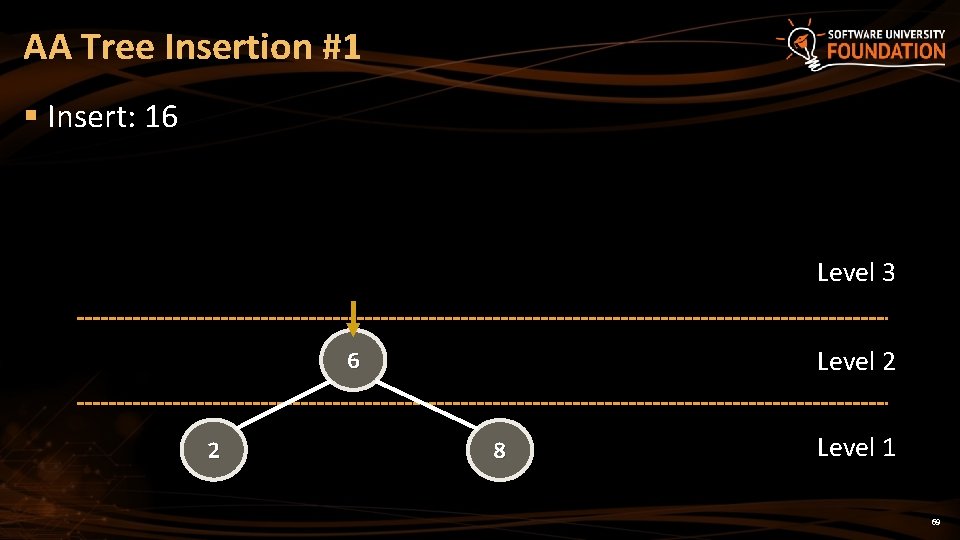
AA Tree Insertion #1 § Insert: 16 Level 3 Level 2 6 2 8 Level 1 69

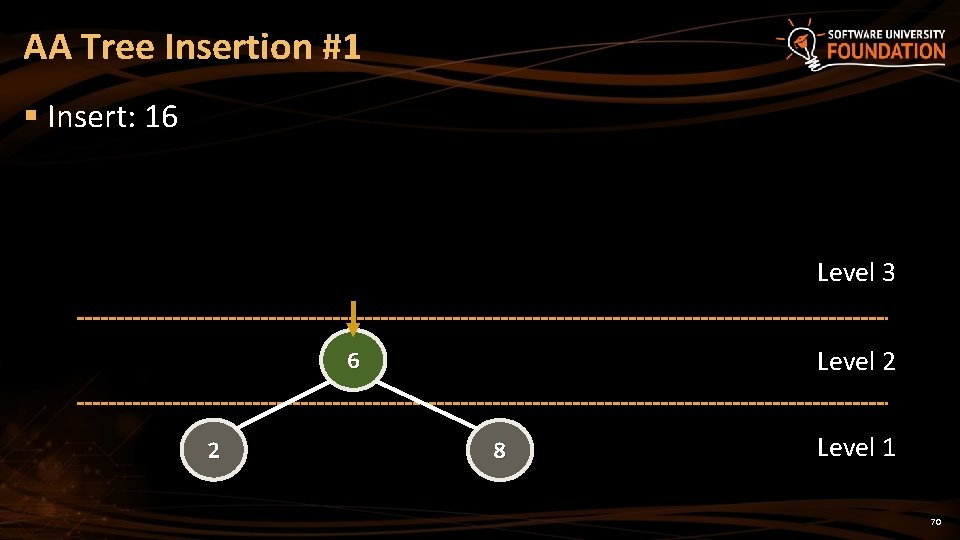
AA Tree Insertion #1 § Insert: 16 Level 3 Level 2 6 2 8 Level 1 70

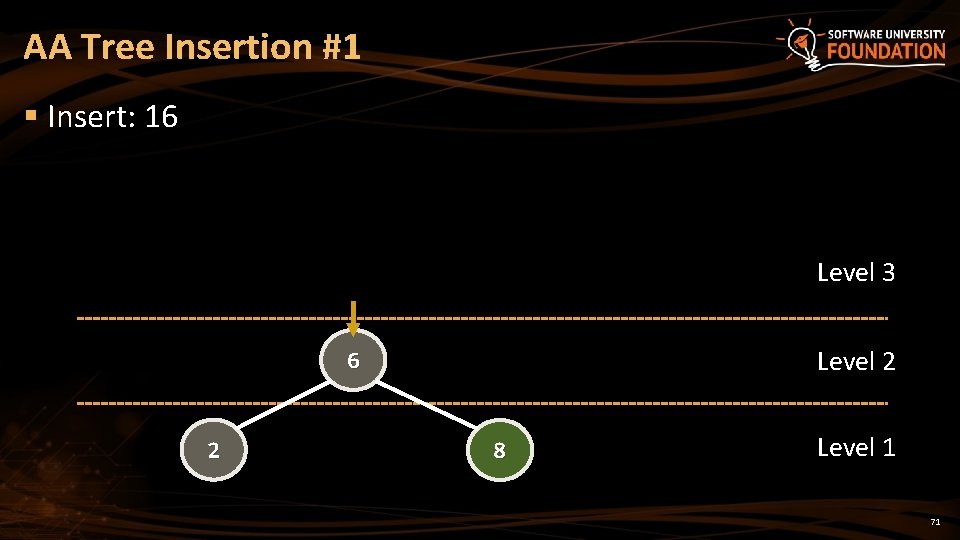
AA Tree Insertion #1 § Insert: 16 Level 3 Level 2 6 2 8 Level 1 71

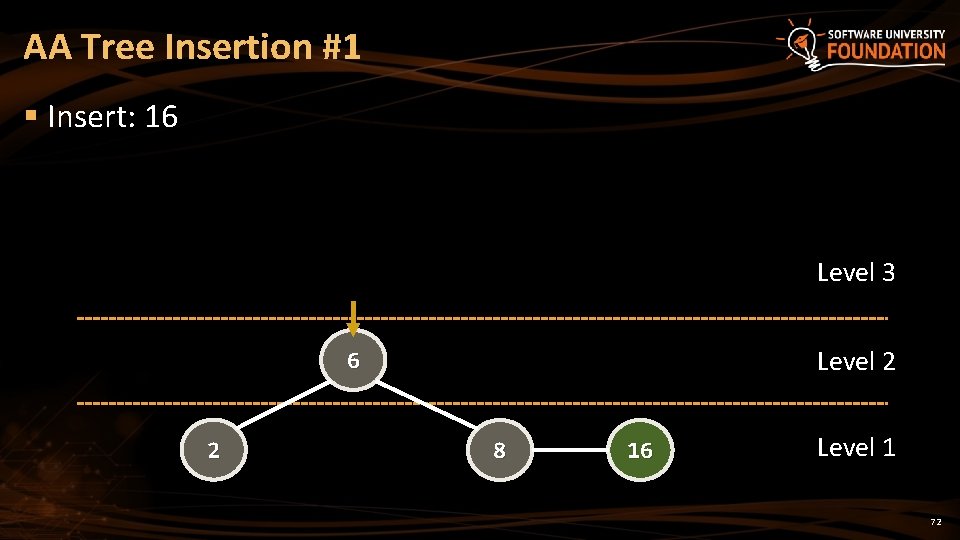
AA Tree Insertion #1 § Insert: 16 Level 3 Level 2 6 2 8 16 Level 1 72

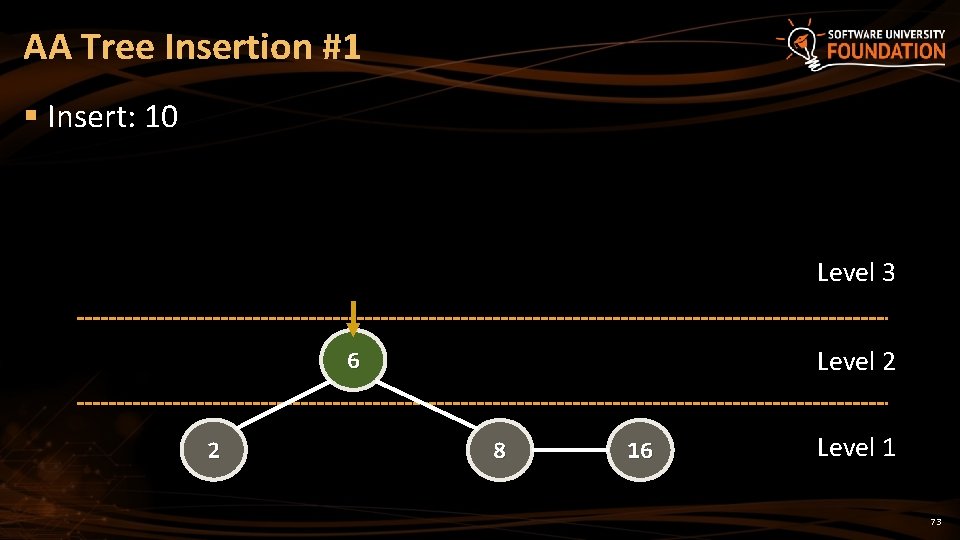
AA Tree Insertion #1 § Insert: 10 Level 3 Level 2 6 2 8 16 Level 1 73

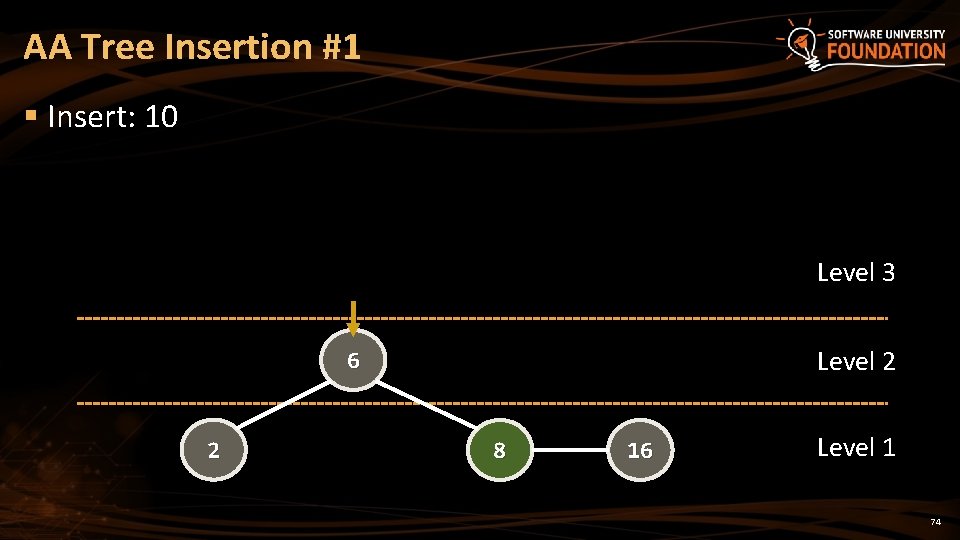
AA Tree Insertion #1 § Insert: 10 Level 3 Level 2 6 2 8 16 Level 1 74

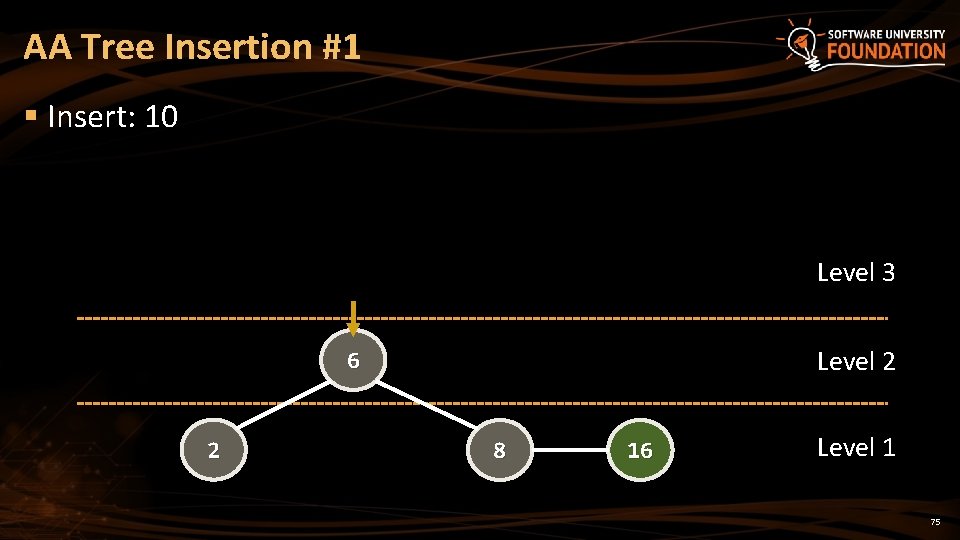
AA Tree Insertion #1 § Insert: 10 Level 3 Level 2 6 2 8 16 Level 1 75

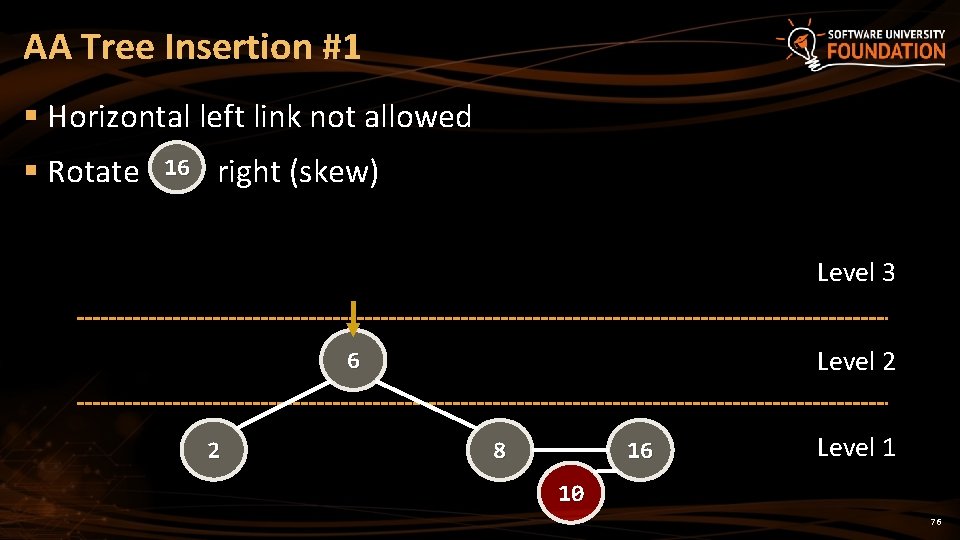
AA Tree Insertion #1 § Horizontal left link not allowed § Rotate 16 right (skew) Level 3 Level 2 6 2 8 16 Level 1 10 76

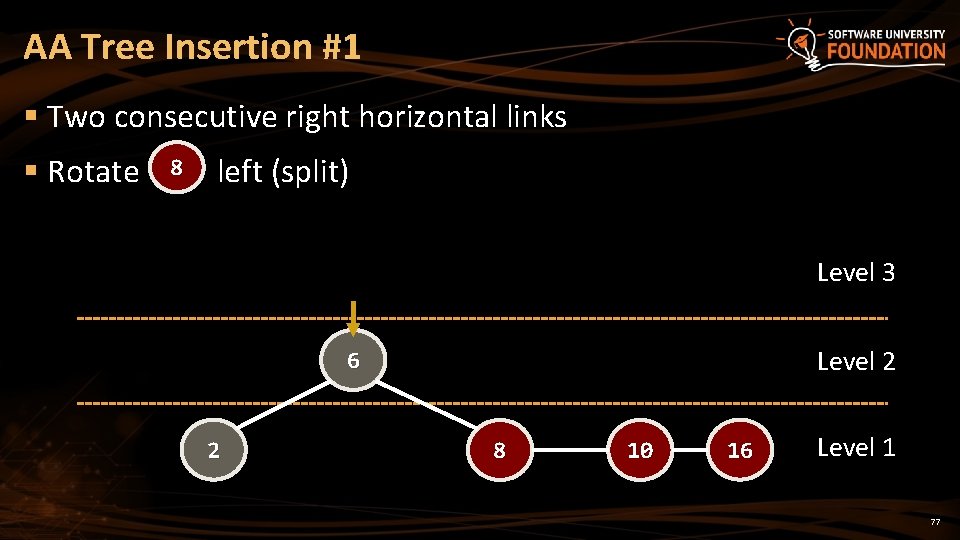
AA Tree Insertion #1 § Two consecutive right horizontal links § Rotate 8 left (split) Level 3 Level 2 6 2 8 10 16 Level 1 77

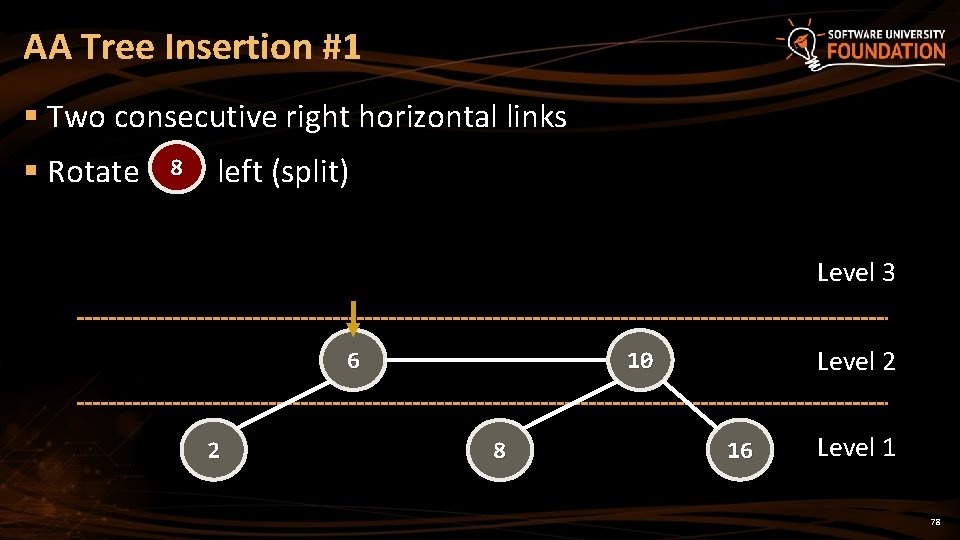
AA Tree Insertion #1 § Two consecutive right horizontal links § Rotate 8 left (split) Level 3 6 2 Level 2 10 8 16 Level 1 78

Trees - Quiz TIME’S UP! TIME: § Consider web application in which § searches are far more frequent than insertions/deletions § Which of the following do you prefer: § AVL § Linked List § Red-Black § B+ 79

Trees - Quiz TIME’S UP! § Consider web application in which § searches are far more frequent than insertions/deletions § Which of the following do you prefer: § AVL § Linked List AVL trees are more rigidly balanced, so they have faster search § Red-Black § B+ 80

Summary § AVL/AA trees tend to be flatter than Red-Black Trees § AVL/AA trees perform more rotations for insertion and deletion § Red-Black trees have faster insertion/deletion § AVL/AA trees have faster searching § AA have simpler implementation 81

AVL Trees, AA Trees ? s n stio e u Q ? ? ? https: //softuni. bg/trainings/1308/data-structures-february-2016

License § This course (slides, examples, labs, videos, homework, etc. ) is licensed under the "Creative Commons Attribution. Non. Commercial-Share. Alike 4. 0 International" license § Attribution: this work may contain portions from § "Fundamentals of Computer Programming with C#" book by Svetlin Nakov & Co. under CC-BY-SA license § "Data Structures and Algorithms" course by Telerik Academy under CC-BY-NC-SA license 83

Free Trainings @ Software University § Software University Foundation – softuni. org § Software University – High-Quality Education, Profession and Job for Software Developers § softuni. bg § Software University @ Facebook § facebook. com/Software. University § Software University @ You. Tube § youtube. com/Software. University § Software University Forums – forum. softuni. bg