AVL Tree 27 th Mar 2007 Outline AVL

AVL Tree 27 th Mar 2007

Outline • AVL Tree – Definition – Properties – Operations 27 th Mar 2007

AVL Trees • Unbalanced Binary Search Trees are bad. Worst case: operations take O(n). • AVL (Adelson-Velskii & Landis) trees maintain balance. • For each node in tree, height of left subtree and height of right subtree differ by a maximum of 1. X H H-1 27 th Mar 2007 X H-2

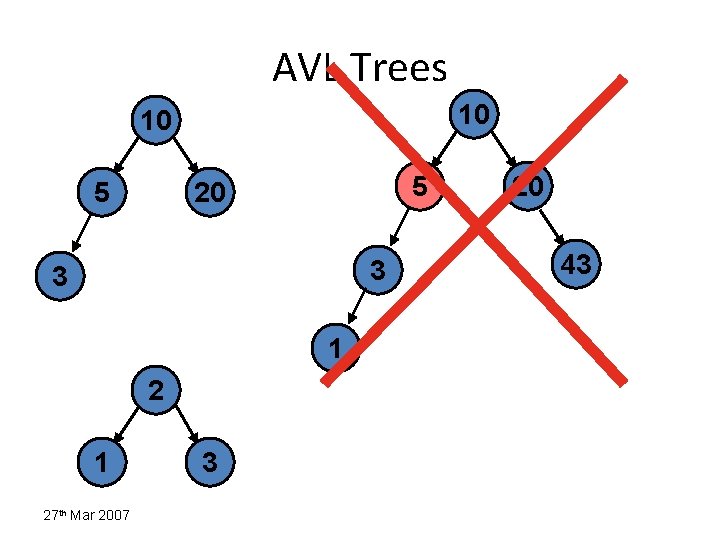
AVL Trees 10 10 5 5 20 3 3 1 27 th Mar 2007 3 20 43

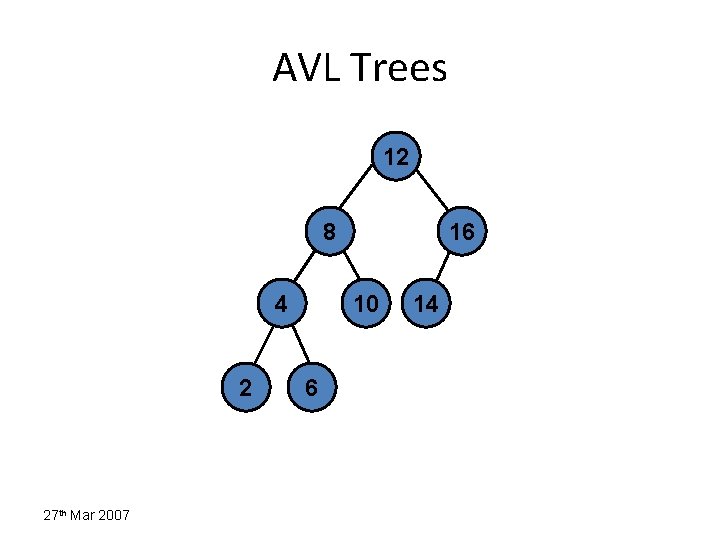
AVL Trees 12 8 4 2 27 th Mar 2007 16 10 6 14

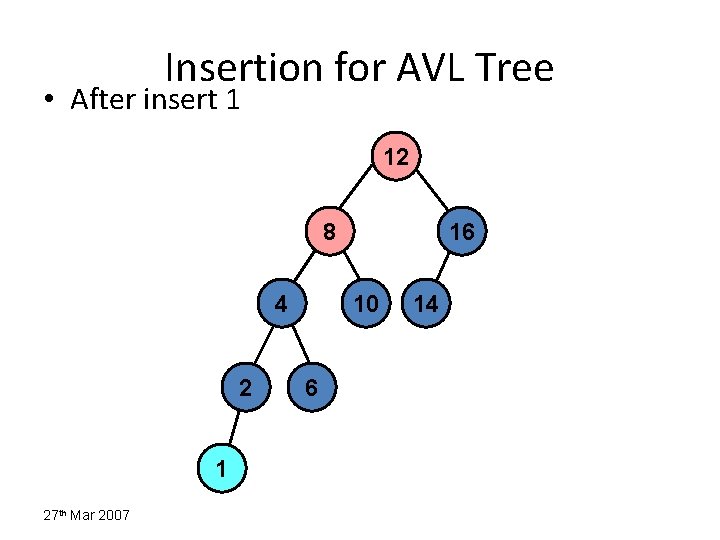
Insertion for AVL Tree • After insert 1 12 8 4 2 1 27 th Mar 2007 16 10 6 14

Insertion for AVL Tree • To ensure balance condition for AVL-tree, after insertion of a new node, we back up the path from the inserted node to root and check the balance condition for each node. • If after insertion, the balance condition does not hold in a certain node, we do one of the following rotations: – Single rotation – Double rotation 27 th Mar 2007

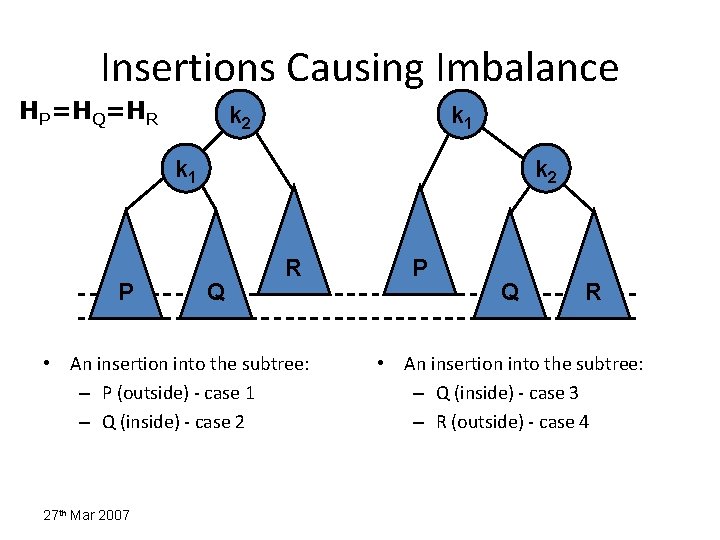
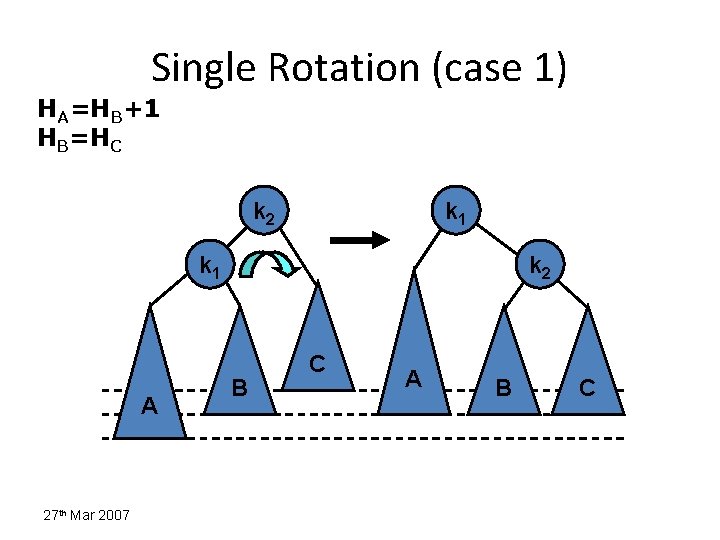
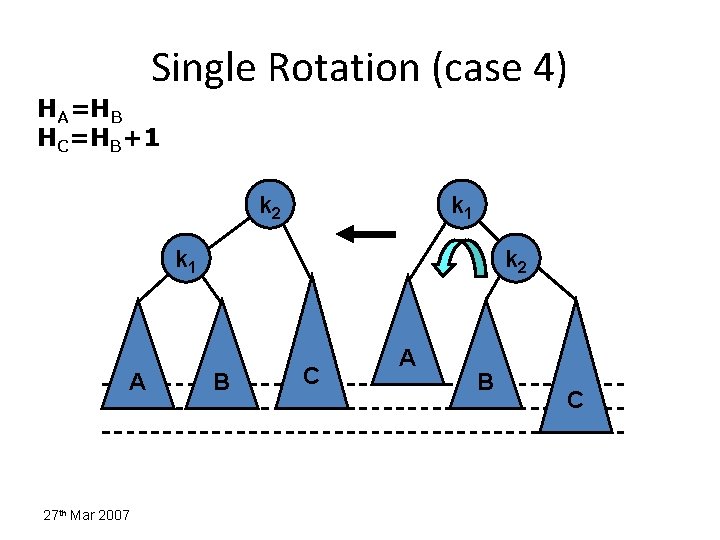
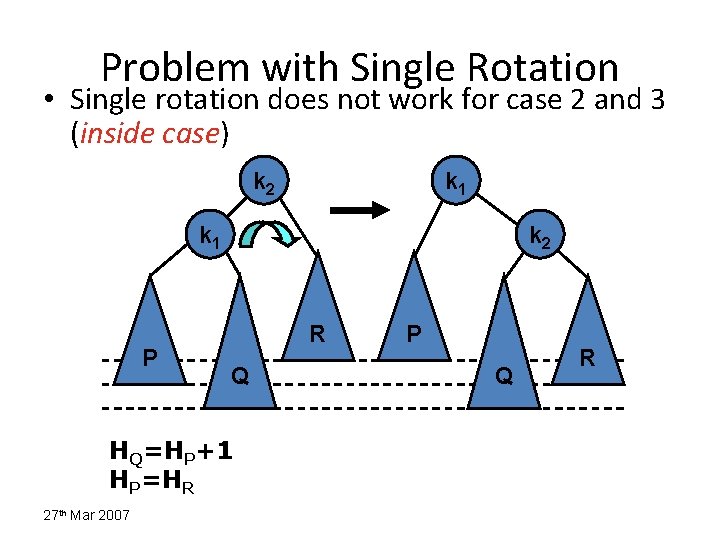
Insertions in AVL Trees Let the node that needs rebalancing be . There are 4 cases: Outside Cases (require single rotation) : 1. Insertion into left subtree of left child of . 2. Insertion into right subtree of right child of . Inside Cases (require double rotation) : 3. Insertion into right subtree of left child of . 4. Insertion into left subtree of right child of . The rebalancing is performed through four separate rotation algorithms. 12/26/03 8

Insertions Causing Imbalance HP=HQ=HR k 2 k 1 P k 2 Q R • An insertion into the subtree: – P (outside) - case 1 – Q (inside) - case 2 27 th Mar 2007 P Q R • An insertion into the subtree: – Q (inside) - case 3 – R (outside) - case 4

Single Rotation (case 1) HA=HB+1 HB=HC k 2 k 1 A 27 th Mar 2007 k 2 B C A B C

Single Rotation (case 4) HA=HB HC=HB+1 k 2 k 1 A 27 th Mar 2007 k 2 B C A B C

Problem with Single Rotation • Single rotation does not work for case 2 and 3 (inside case) k 2 k 1 P k 2 R Q HQ=HP+1 HP=HR 27 th Mar 2007 P Q R

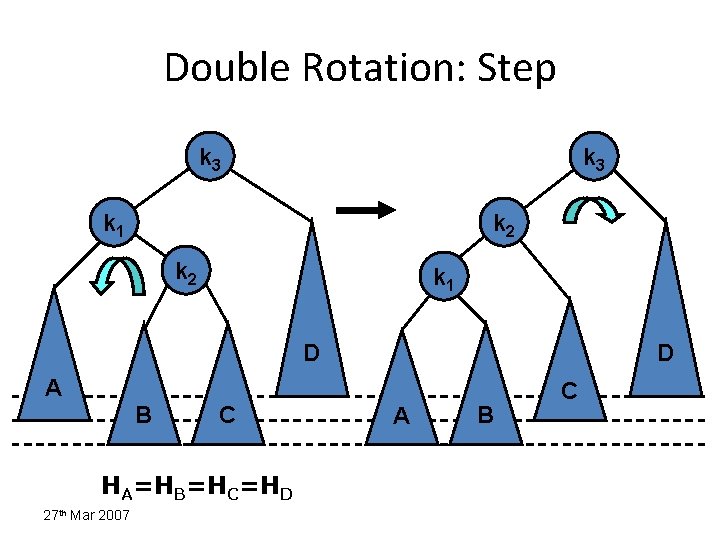
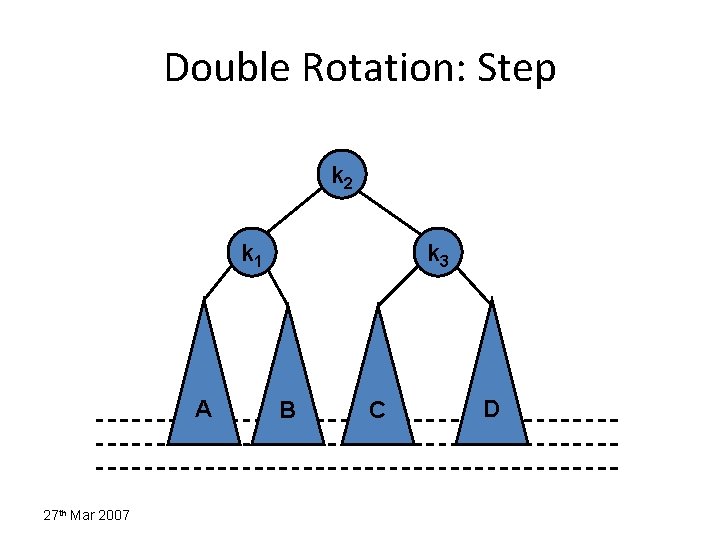
Double Rotation: Step k 3 k 1 k 2 k 1 D D A B C HA=HB=HC=HD 27 th Mar 2007 A B C

Double Rotation: Step k 2 k 1 A 27 th Mar 2007 k 3 B C D

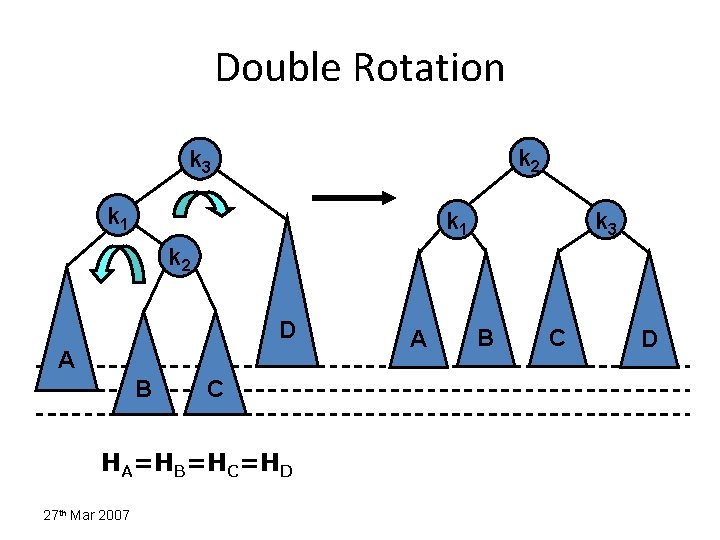
Double Rotation k 2 k 3 k 1 k 3 k 2 D A B C HA=HB=HC=HD 27 th Mar 2007 A B C D

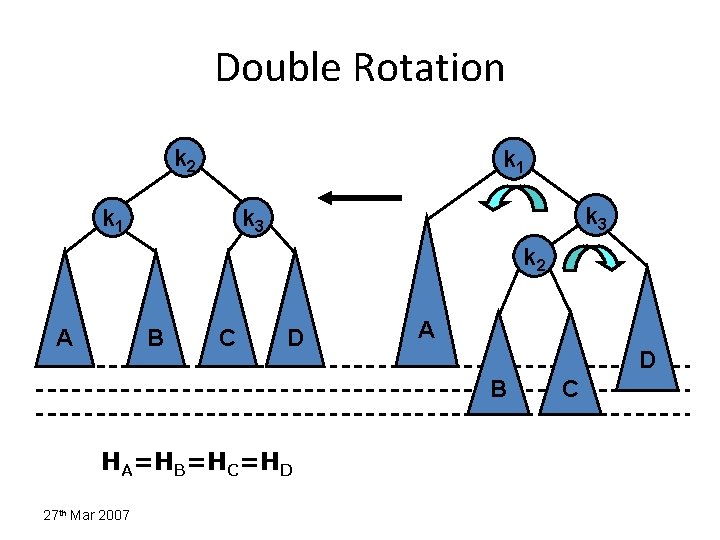
Double Rotation k 2 k 1 k 3 k 2 A B C D A D B HA=HB=HC=HD 27 th Mar 2007 C

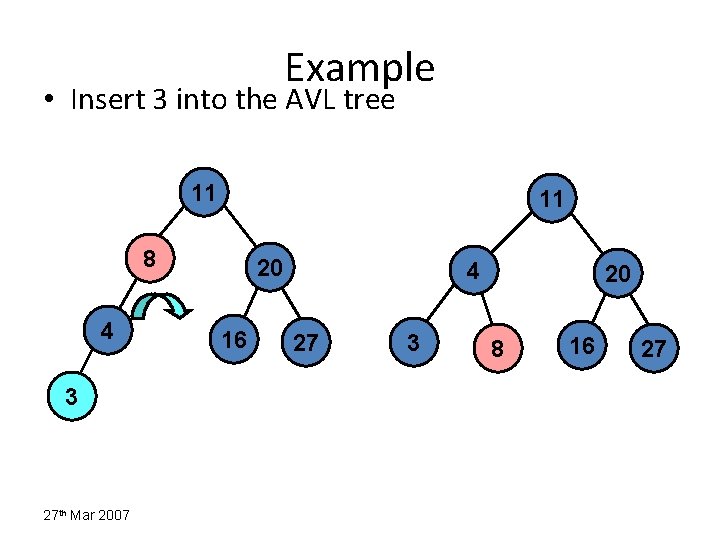
Example • Insert 3 into the AVL tree 11 11 8 4 3 27 th Mar 2007 20 16 4 27 3 20 8 16 27

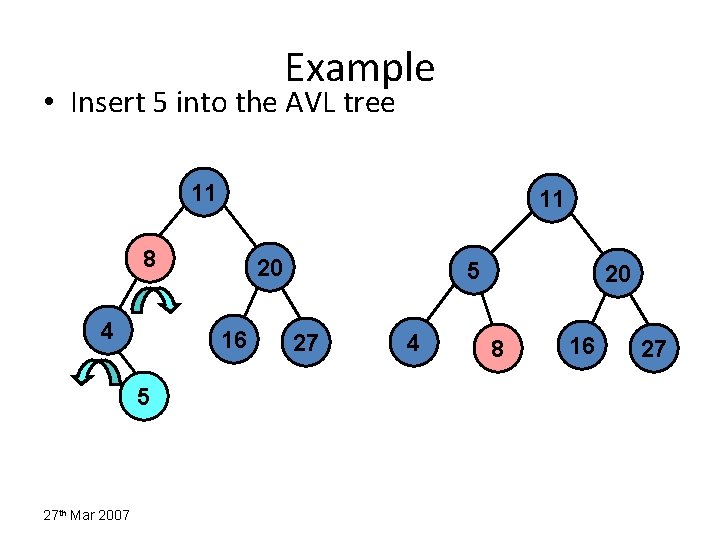
Example • Insert 5 into the AVL tree 11 11 8 4 16 5 27 th Mar 2007 20 5 27 4 20 8 16 27

AVL Trees: Exercise • Insertion order: – 10, 85, 15, 70, 20, 60, 30, 50, 65, 80, 90, 40, 5, 55 27 th Mar 2007

Remove Operation in AVL Tree • Removing a node from an AVL Tree is the same as removing from a binary search tree. However, it may unbalance the tree. • Similar to insertion, starting from the removed node we check all the nodes in the path up to the root for the first unbalance node. • Use the appropriate single or double rotation to balance the tree. • May need to continue searching for unbalanced nodes all the way to the root. 27 th Mar 2007

Deletion X in AVL Trees • Deletion: – Case 1: if X is a leaf, delete X – Case 2: if X has 1 child, use it to replace X – Case 3: if X has 2 children, replace X with its inorder predecessor (and recursively delete it) • Rebalancing 27 th Mar 2007

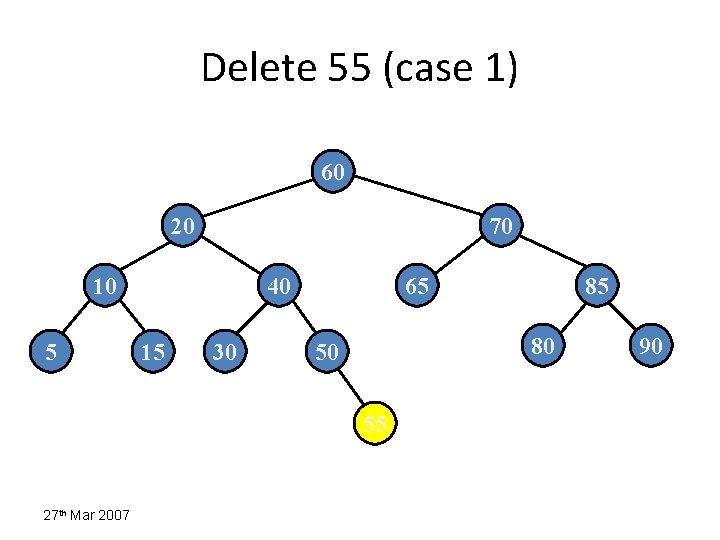
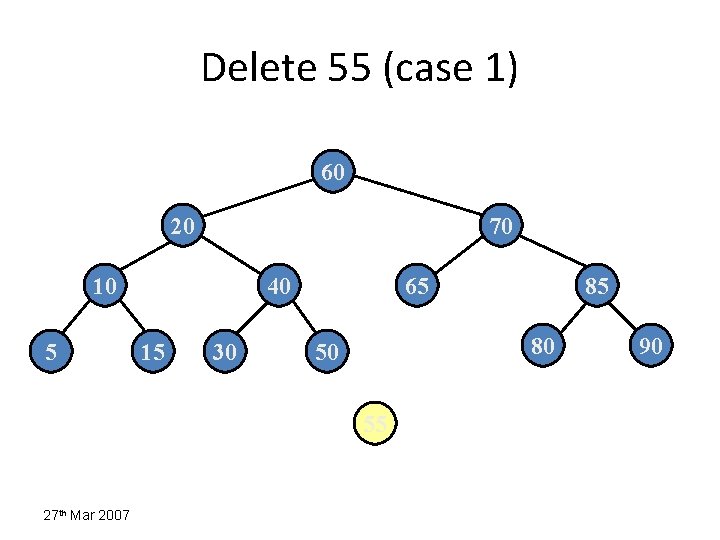
Delete 55 (case 1) 60 20 70 10 5 40 15 30 65 80 50 55 27 th Mar 2007 85 90

Delete 55 (case 1) 60 20 70 10 5 40 15 30 65 80 50 55 27 th Mar 2007 85 90

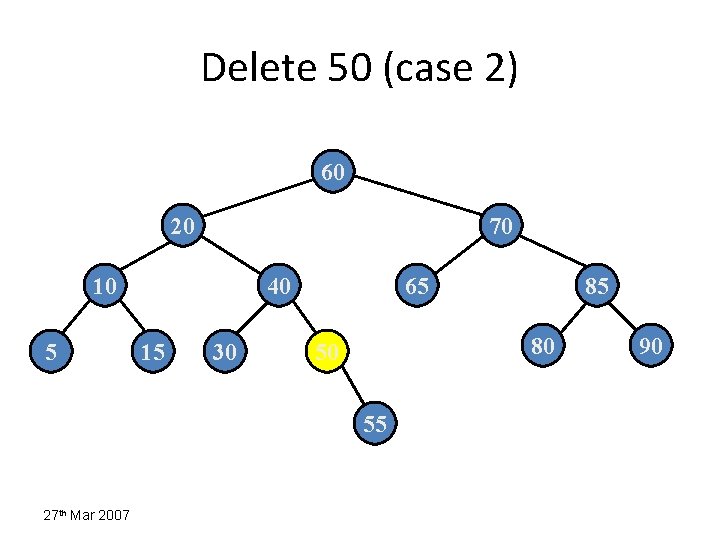
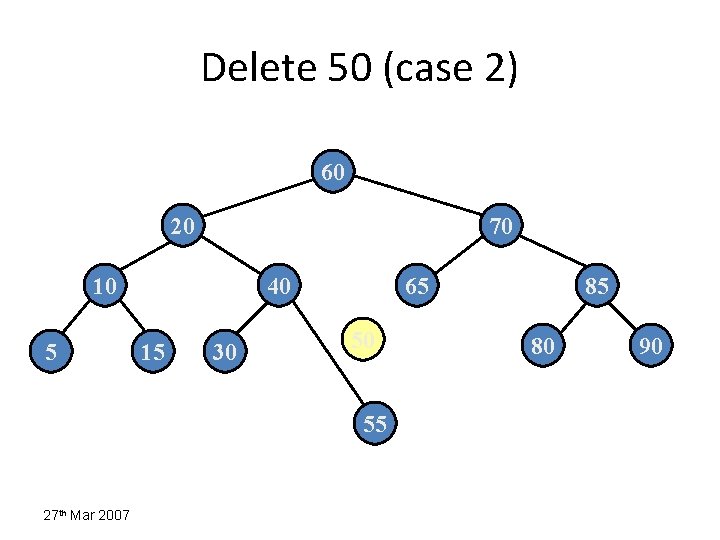
Delete 50 (case 2) 60 20 70 10 5 40 15 30 65 80 50 55 27 th Mar 2007 85 90

Delete 50 (case 2) 60 20 70 10 5 40 15 30 65 50 55 27 th Mar 2007 85 80 90

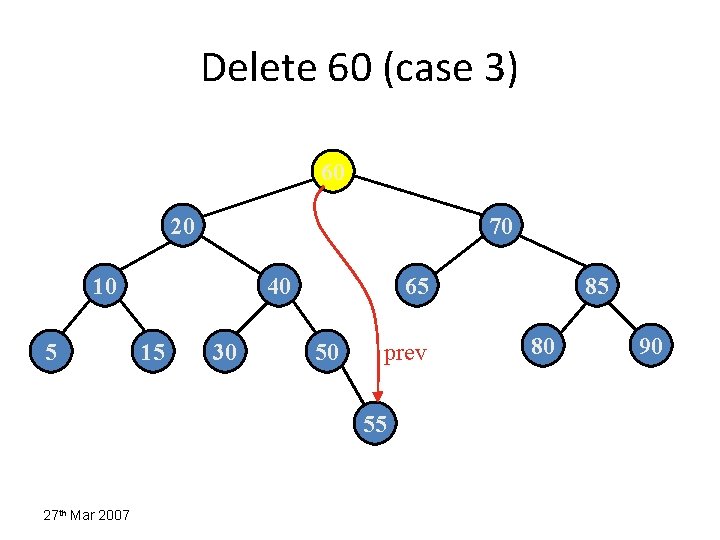
Delete 60 (case 3) 60 20 70 10 5 40 15 30 65 50 prev 55 27 th Mar 2007 85 80 90

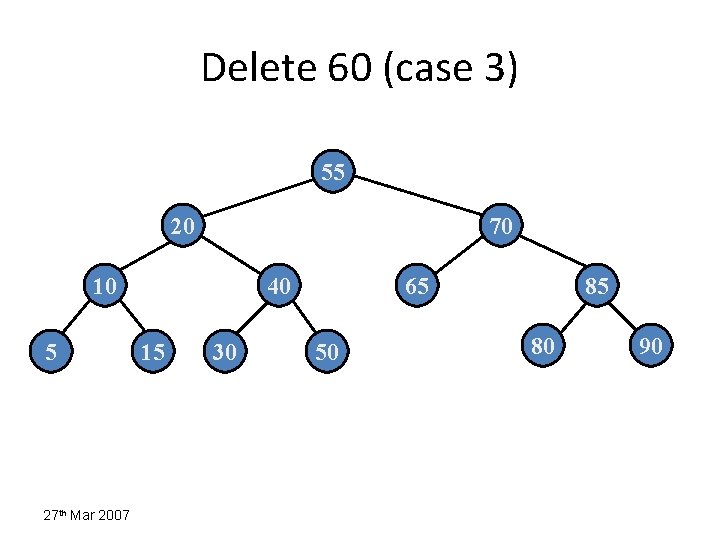
Delete 60 (case 3) 55 20 70 10 5 27 th Mar 2007 40 15 30 65 50 85 80 90

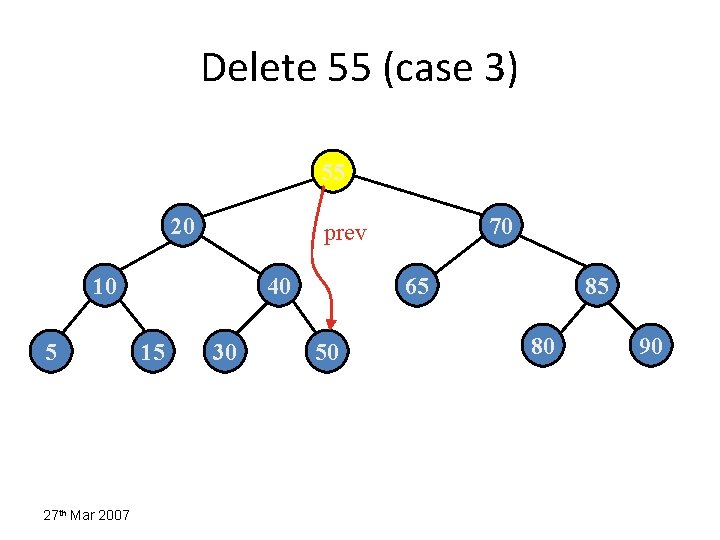
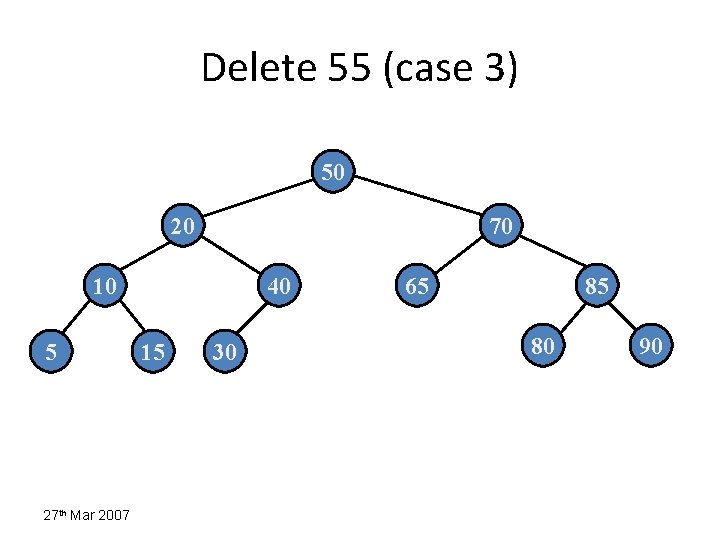
Delete 55 (case 3) 55 20 10 5 27 th Mar 2007 40 15 70 prev 30 65 50 85 80 90

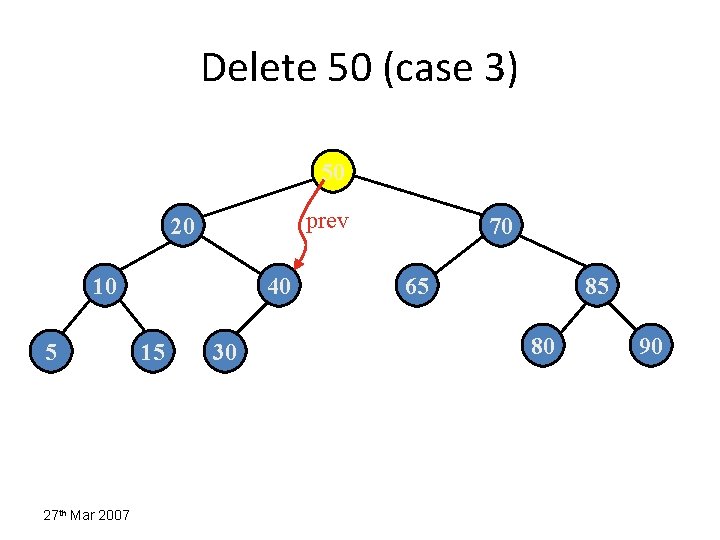
Delete 55 (case 3) 50 20 70 10 5 27 th Mar 2007 40 15 30 65 85 80 90

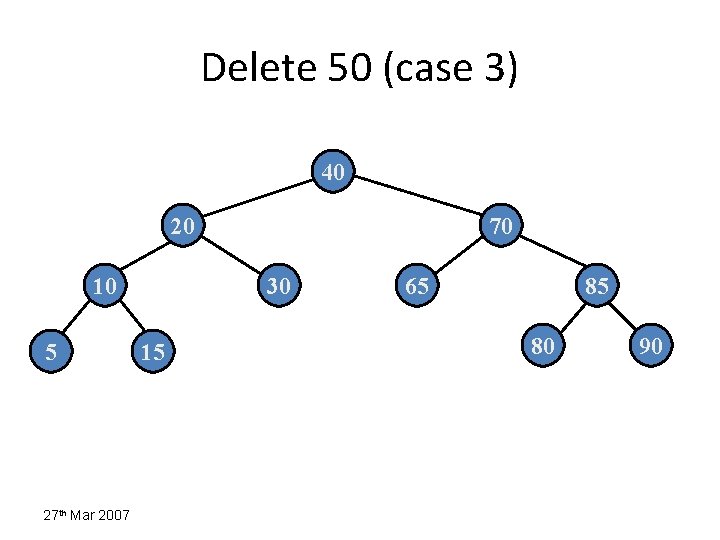
Delete 50 (case 3) 50 prev 20 10 5 27 th Mar 2007 40 15 30 70 65 85 80 90

Delete 50 (case 3) 40 20 10 5 27 th Mar 2007 70 30 15 65 85 80 90

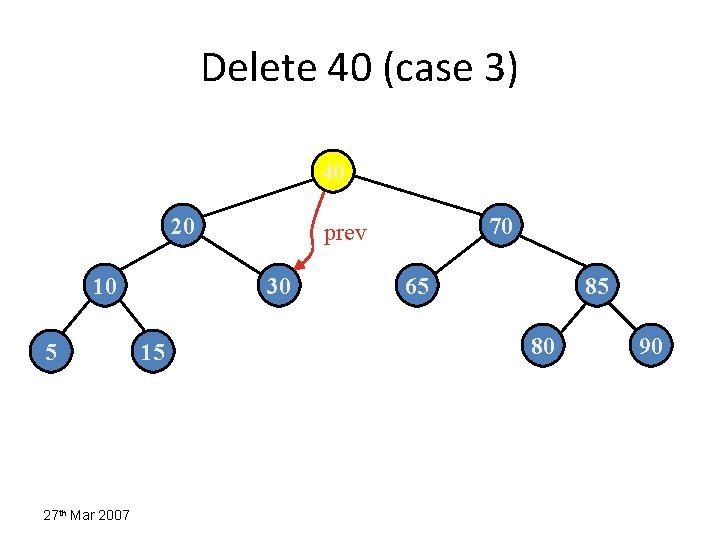
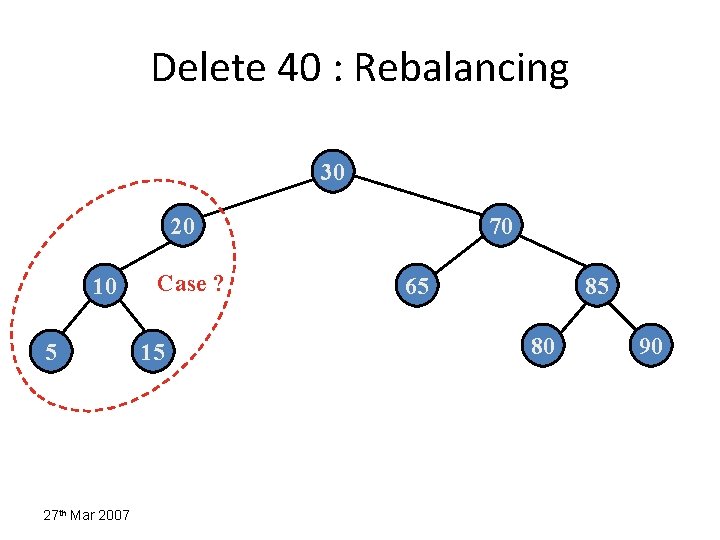
Delete 40 (case 3) 40 20 10 5 27 th Mar 2007 30 15 70 prev 65 85 80 90

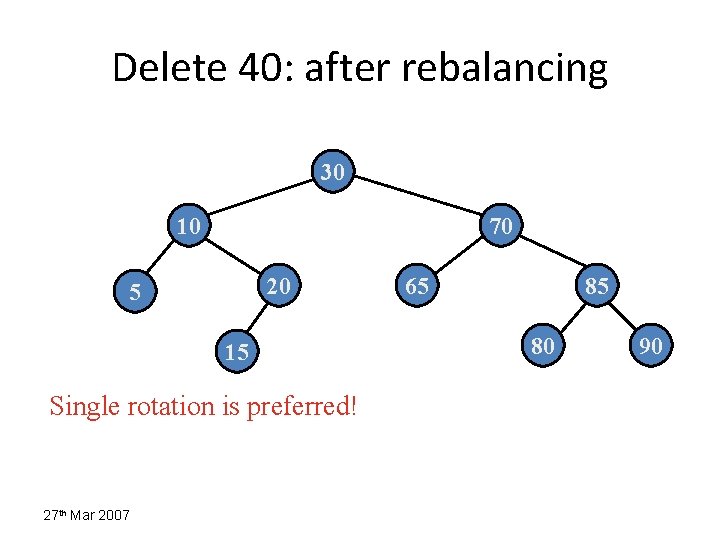
Delete 40 : Rebalancing 30 20 10 5 27 th Mar 2007 Case ? 15 70 65 85 80 90

Delete 40: after rebalancing 30 10 70 20 5 15 Single rotation is preferred! 27 th Mar 2007 65 85 80 90

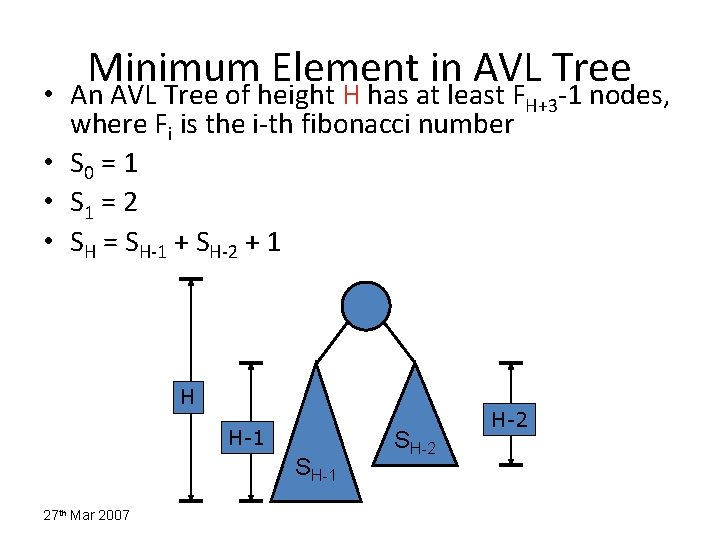
Minimum Element in AVL Tree • An AVL Tree of height H has at least FH+3 -1 nodes, where Fi is the i-th fibonacci number • S 0 = 1 • S 1 = 2 • SH = SH-1 + SH-2 + 1 H H-1 SH-1 27 th Mar 2007 SH-2

AVL Tree: analysis (1) 27 th Mar 2007

AVL Tree: analysis (2) • The depth of AVL Trees is at most logarithmic. • So, all of the operations on AVL trees are also logarithmic. • The worst-case height is at most 44 percent more than the minimum possible for binary trees. 27 th Mar 2007

Summary • Find element, insert element, and remove element operations all have complexity O(log n) for worst case • Insert operation: top-down insertion and bottom up balancing 27 th Mar 2007

Further Study • http: //telaga. cs. ui. ac. id/Web. Ku liah/IKI 10100/resources/animati on/datastructure/avltree. html • Section 19. 4 of Weiss book 27 th Mar 2007