AVL Tree 27 th Mar 2007 AVL Trees

AVL Tree 27 th Mar 2007

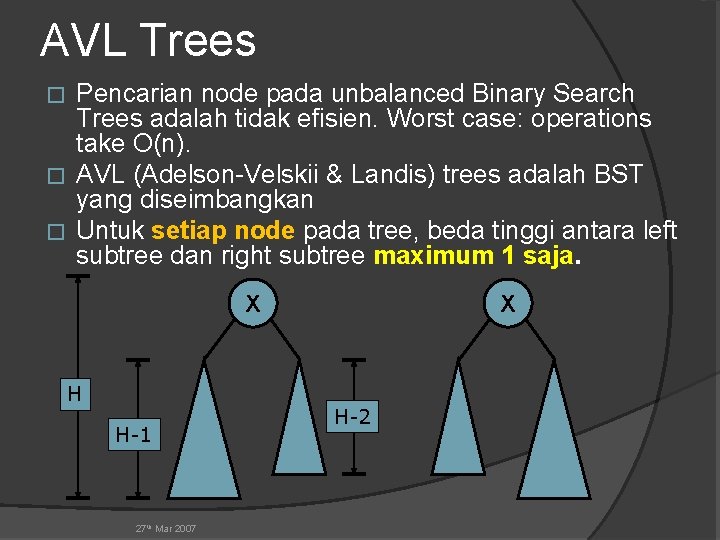
AVL Trees Pencarian node pada unbalanced Binary Search Trees adalah tidak efisien. Worst case: operations take O(n). � AVL (Adelson-Velskii & Landis) trees adalah BST yang diseimbangkan � Untuk setiap node pada tree, beda tinggi antara left subtree dan right subtree maximum 1 saja. � X H H-1 27 th Mar 2007 X H-2

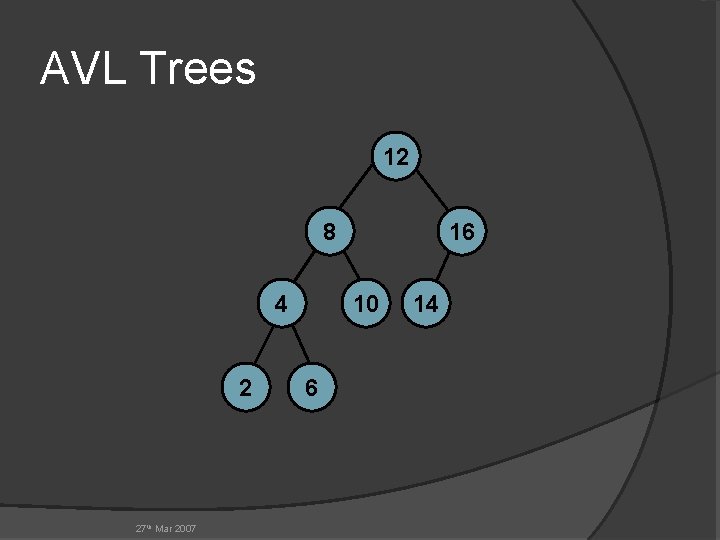
AVL Trees 12 8 4 2 27 th Mar 2007 16 10 6 14

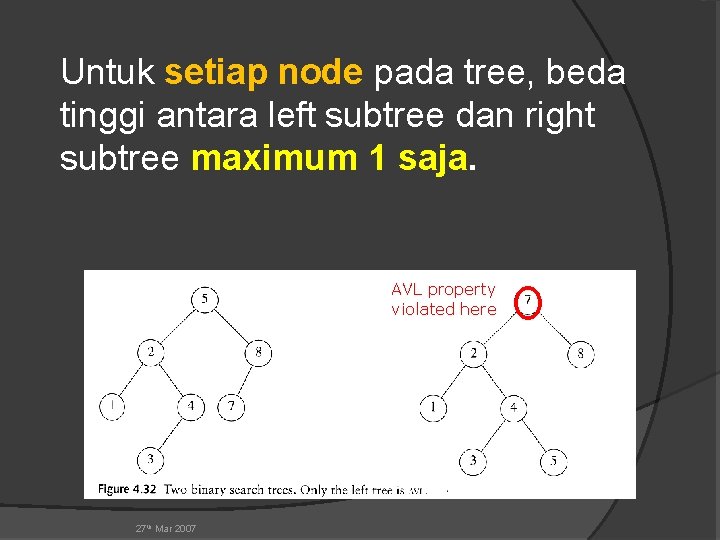
Untuk setiap node pada tree, beda tinggi antara left subtree dan right subtree maximum 1 saja. AVL property violated here 27 th Mar 2007

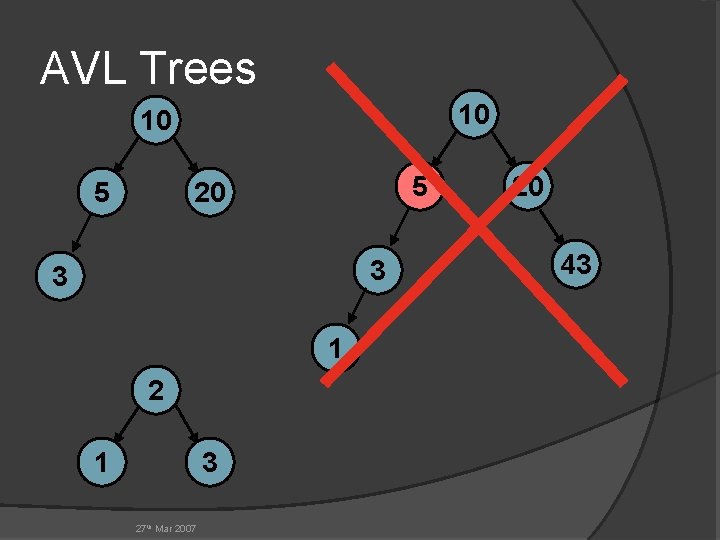
AVL Trees 10 10 5 5 20 3 3 1 2 1 3 27 th Mar 2007 20 43

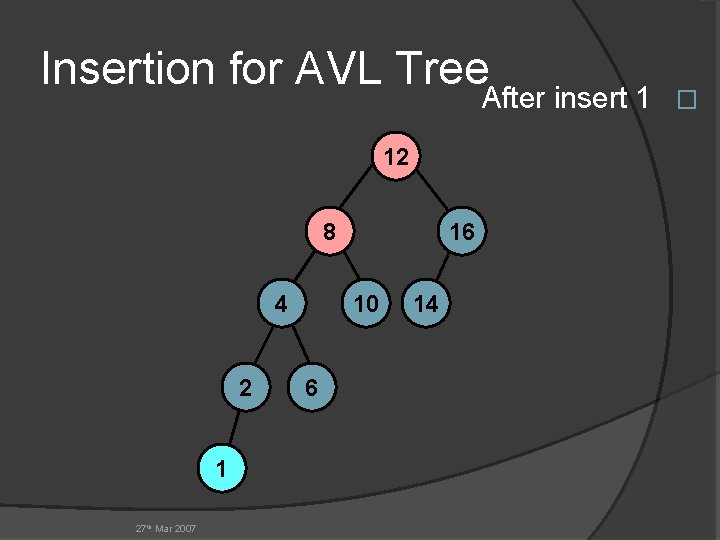
Insertion for AVL Tree After insert 1 � 12 8 4 2 1 27 th Mar 2007 16 10 6 14

Insertion for AVL Tree � Untuk memastikan AVL-tree dalam kondisi seimbang, setelah suatu node di -insert-kan, perlu dicek keseimbangan untuk tiap node � Jika setelah insertion ada node yang tidak seimbang, maka dilakukan operasi berikut : Single rotation Double rotation 27 th Mar 2007

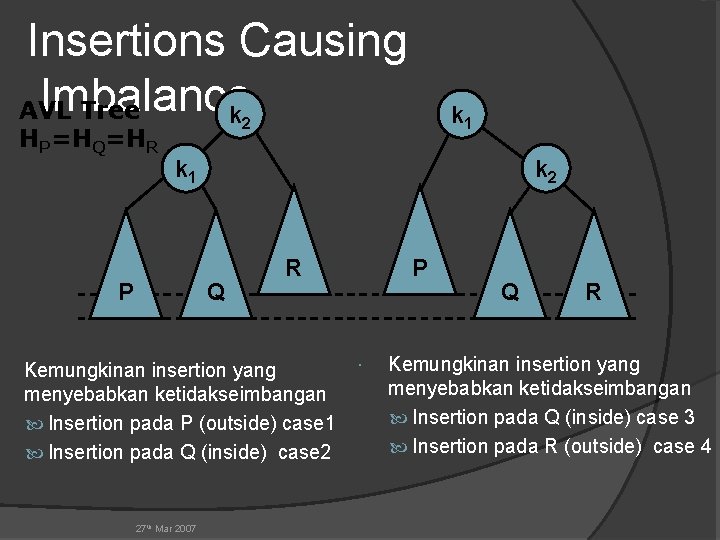
Insertions Causing Imbalance AVL Tree k HP=HQ=HR k 1 2 k 1 P k 2 Q R Kemungkinan insertion yang menyebabkan ketidakseimbangan Insertion pada P (outside) case 1 Insertion pada Q (inside) case 2 27 th Mar 2007 P Q R Kemungkinan insertion yang menyebabkan ketidakseimbangan Insertion pada Q (inside) case 3 Insertion pada R (outside) case 4

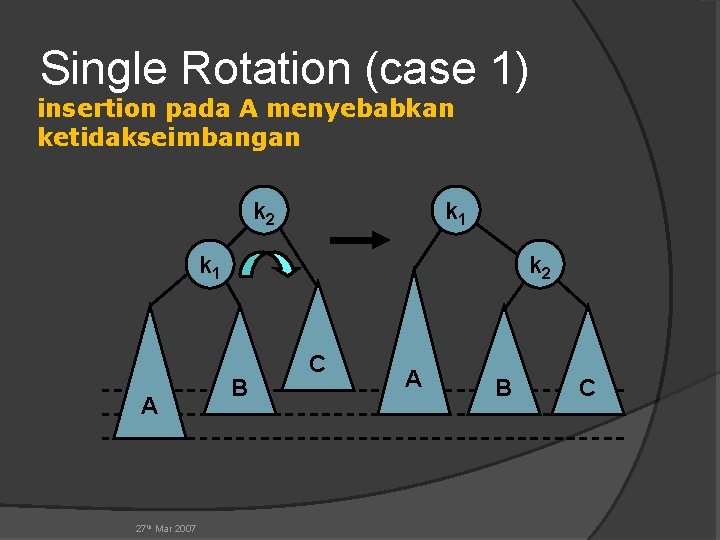
Single Rotation (case 1) insertion pada A menyebabkan ketidakseimbangan k 2 k 1 A 27 th Mar 2007 k 2 B C A B C

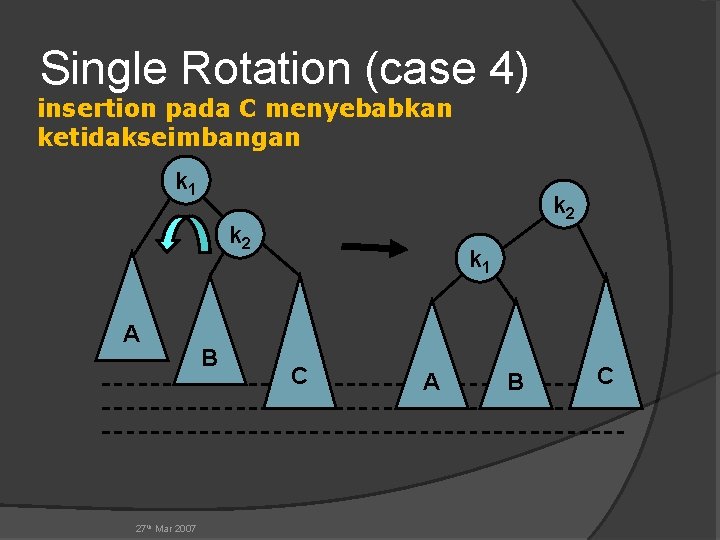
Single Rotation (case 4) insertion pada C menyebabkan ketidakseimbangan k 1 k 2 A 27 th Mar 2007 B k 1 C A B C

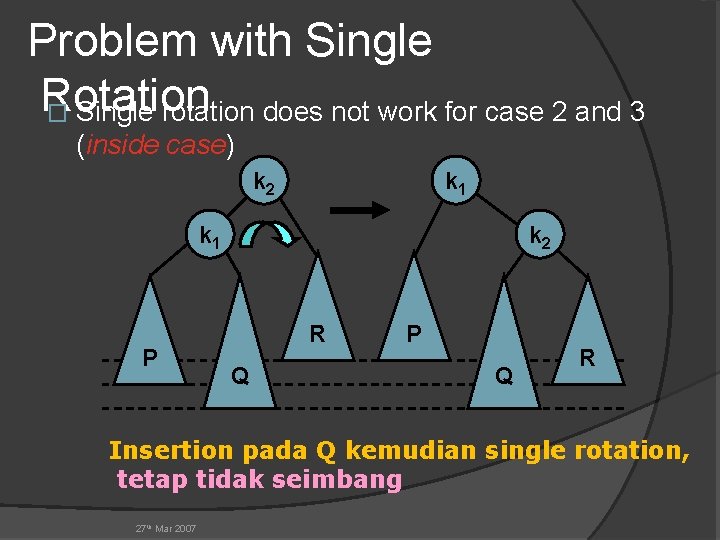
Problem with Single Rotation � Single rotation does not work for case 2 and 3 (inside case) k 2 k 1 P k 2 R Q P Q R Insertion pada Q kemudian single rotation, tetap tidak seimbang 27 th Mar 2007

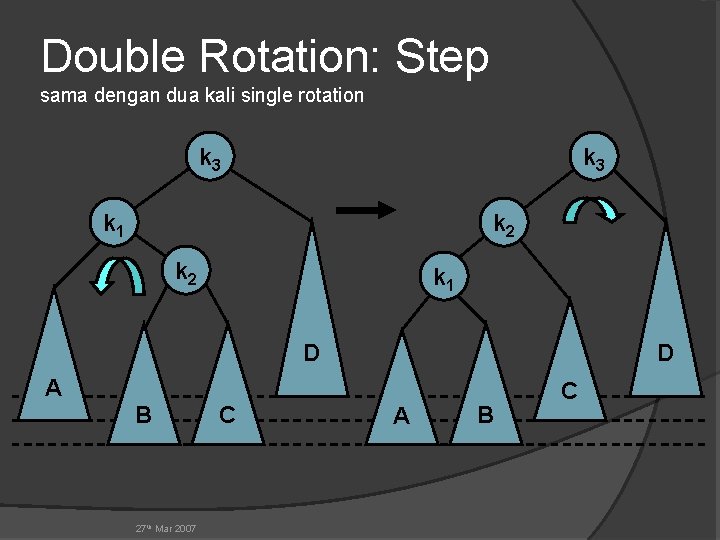
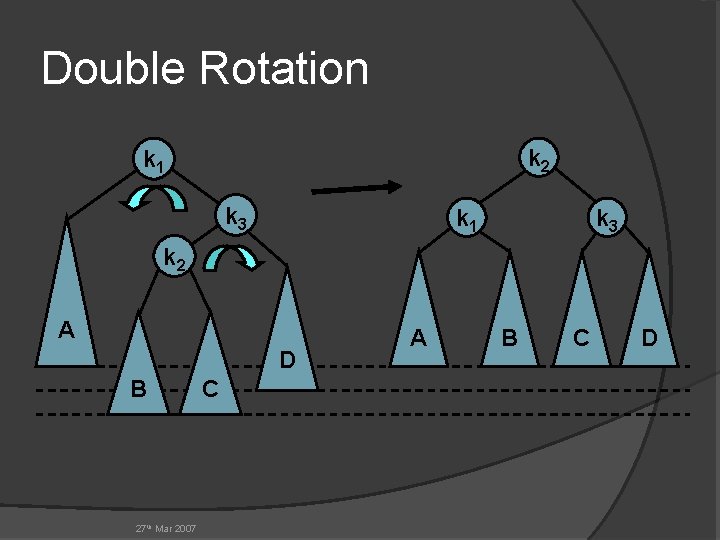
Double Rotation: Step sama dengan dua kali single rotation k 3 k 1 k 2 k 1 D D A B 27 th Mar 2007 C A B C

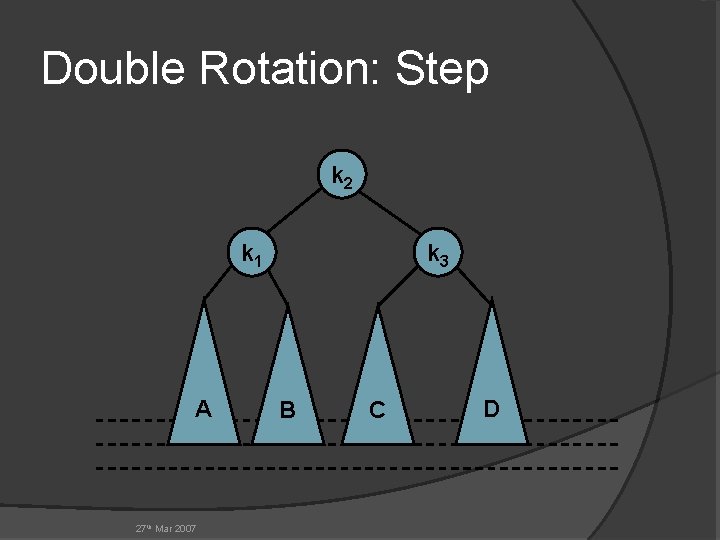
Double Rotation: Step k 2 k 1 A 27 th Mar 2007 k 3 B C D

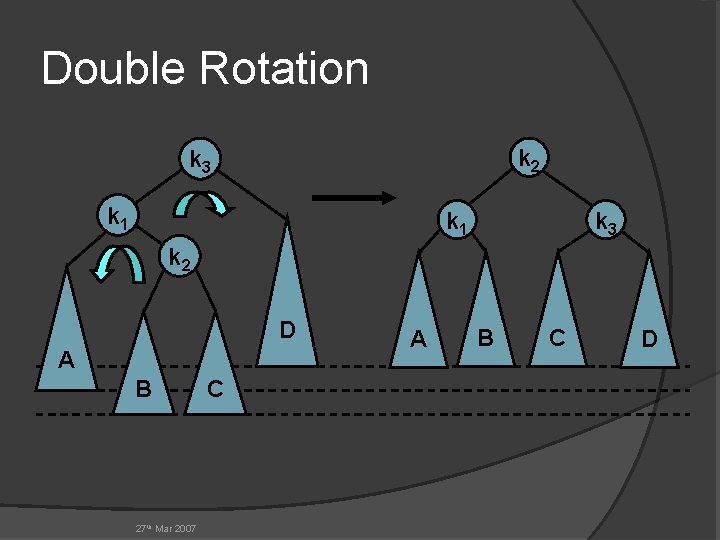
Double Rotation k 2 k 3 k 1 k 3 k 2 D A B 27 th Mar 2007 C A B C D

Double Rotation k 2 k 1 k 3 k 2 A D B 27 th Mar 2007 C A B C D

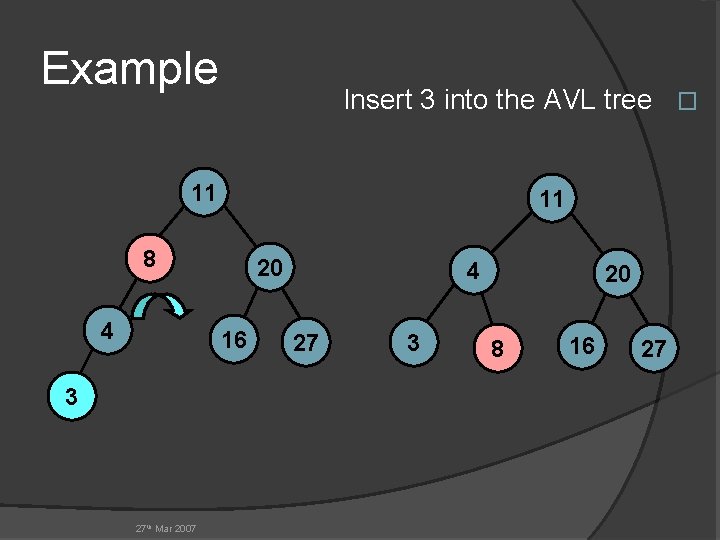
Example Insert 3 into the AVL tree � 11 11 8 4 20 16 3 27 th Mar 2007 4 27 3 20 8 16 27

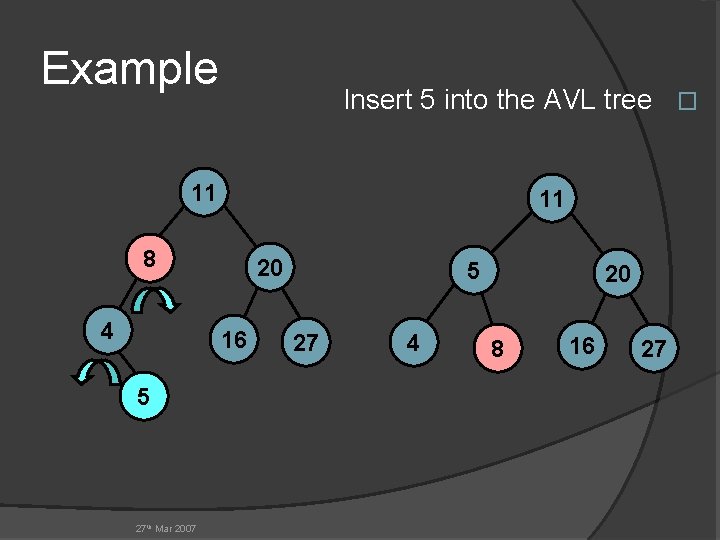
Example Insert 5 into the AVL tree � 11 11 8 4 20 16 5 27 th Mar 2007 5 27 4 20 8 16 27

AVL Trees: Exercise � Insertion order: � 10, 85, 15, 70, 20, 60, 30, 50, 65, 80, 90, 40, 5, 55 27 th Mar 2007

Remove Operation in AVL Tree Removing a node from an AVL Tree is the same as removing from a binary search tree. However, it may unbalance the tree. � Similar to insertion, starting from the removed node we check all the nodes in the path up to the root for the first unbalance node. � Use the appropriate single or double rotation to balance the tree. � May need to continue searching for unbalanced nodes all the way to the root. � 27 th Mar 2007

Deletion X in AVL Trees � Deletion: �Case 1: if X is a leaf, delete X �Case 2: if X has 1 child, use it to replace X �Case 3: if X has 2 children, replace X with its inorder predecessor (and recursively delete it) � Rebalancing 27 th Mar 2007

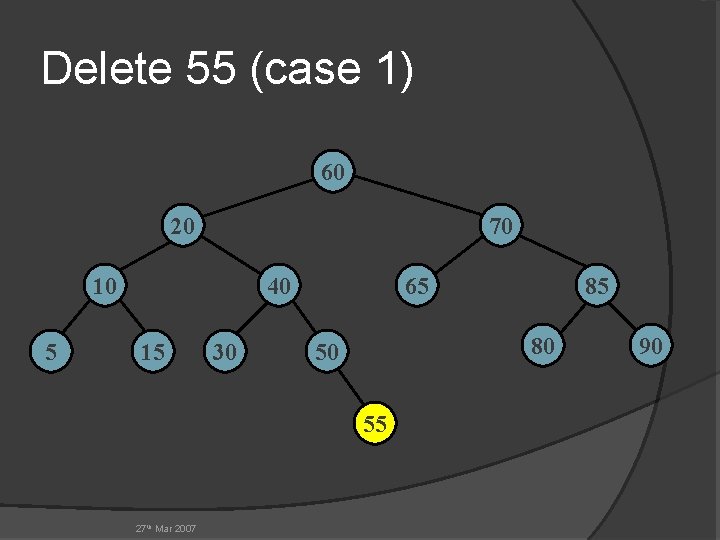
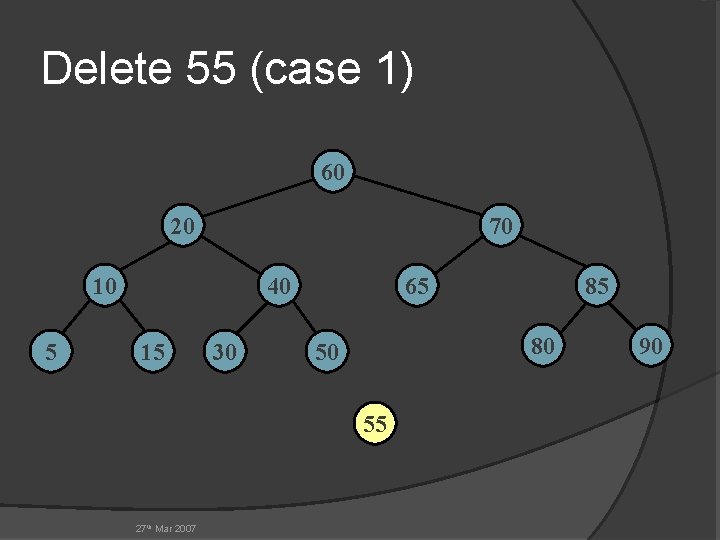
Delete 55 (case 1) 60 20 70 10 5 40 15 30 65 80 50 55 27 th Mar 2007 85 90

Delete 55 (case 1) 60 20 70 10 5 40 15 30 65 80 50 55 27 th Mar 2007 85 90

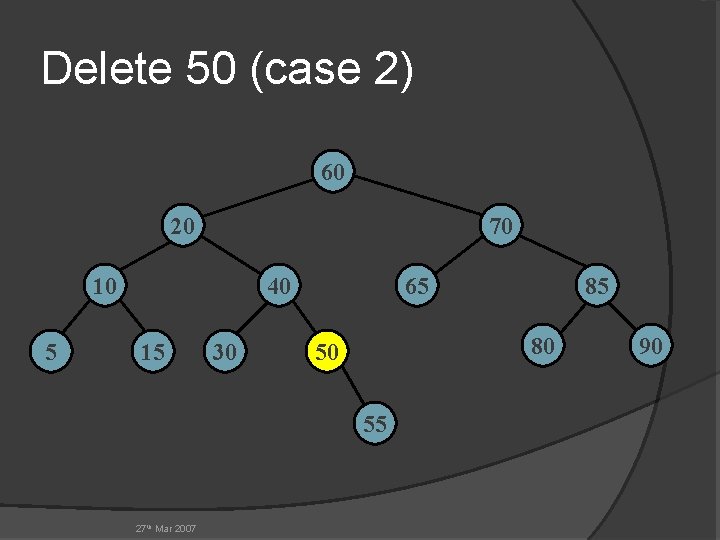
Delete 50 (case 2) 60 20 70 10 5 40 15 30 65 80 50 55 27 th Mar 2007 85 90

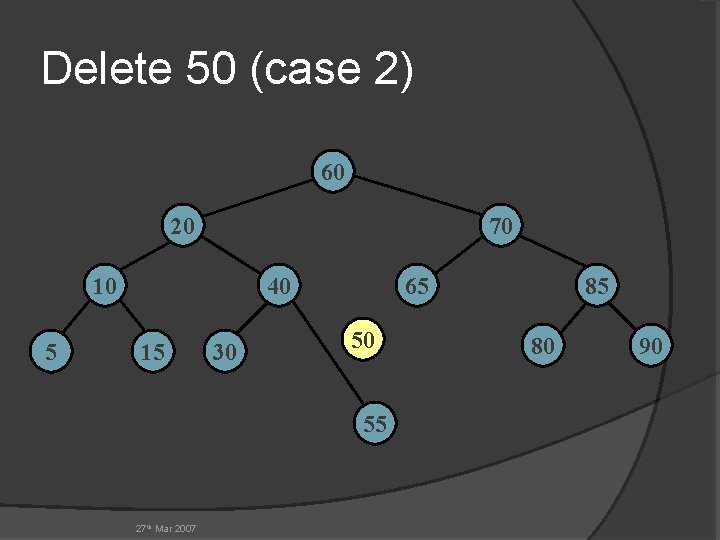
Delete 50 (case 2) 60 20 70 10 5 40 15 30 65 50 55 27 th Mar 2007 85 80 90

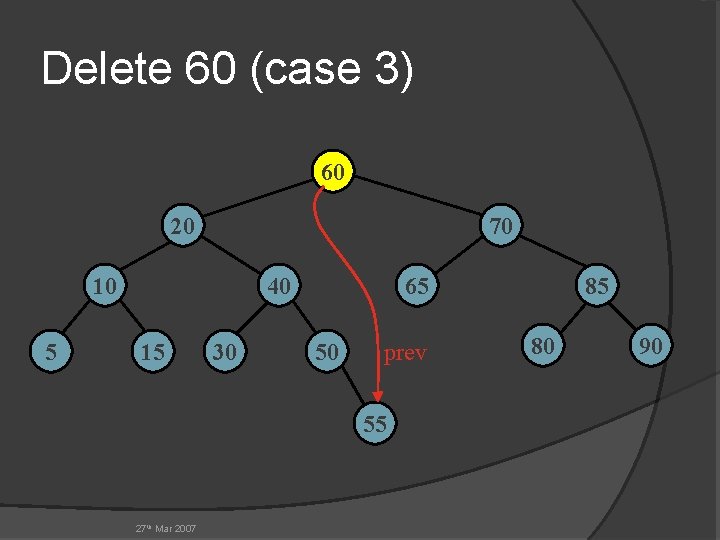
Delete 60 (case 3) 60 20 70 10 5 40 15 30 65 50 prev 55 27 th Mar 2007 85 80 90

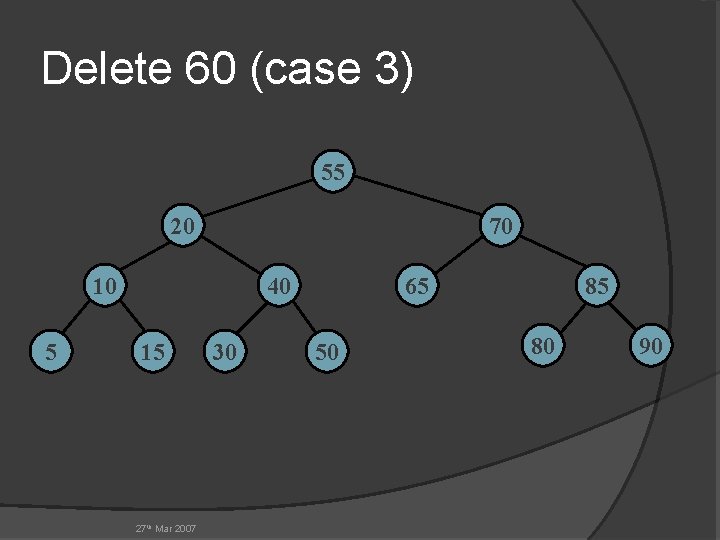
Delete 60 (case 3) 55 20 70 10 5 40 15 27 th Mar 2007 30 65 50 85 80 90

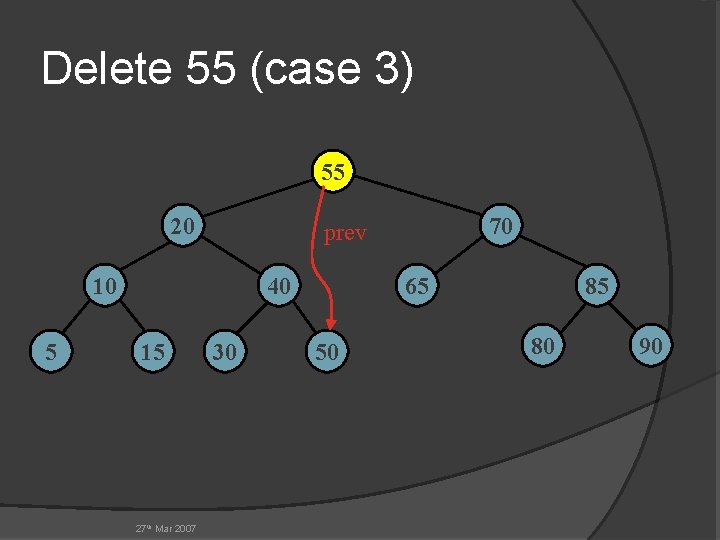
Delete 55 (case 3) 55 20 10 5 40 15 27 th Mar 2007 70 prev 30 65 50 85 80 90

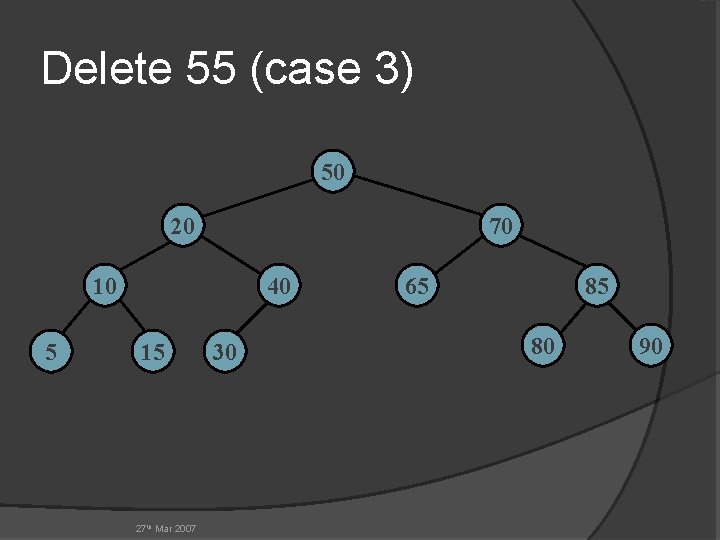
Delete 55 (case 3) 50 20 70 10 5 40 15 27 th Mar 2007 30 65 85 80 90

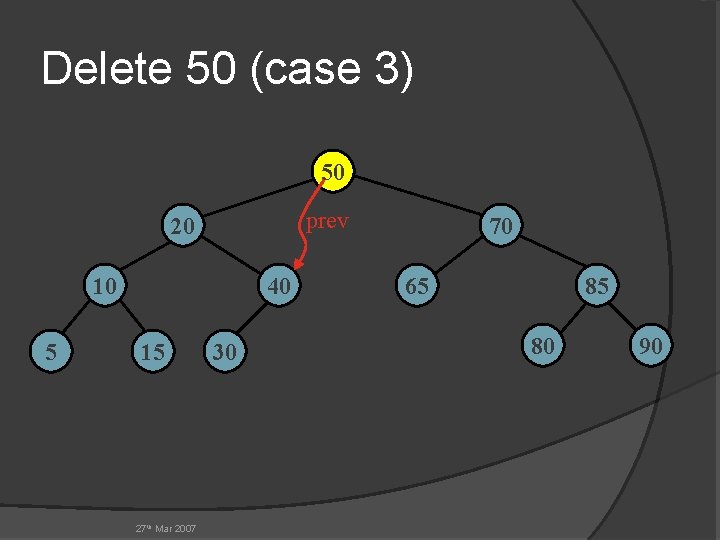
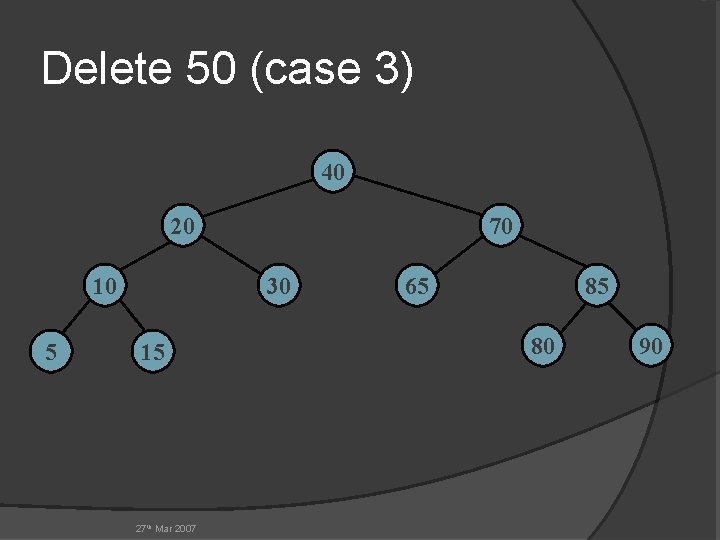
Delete 50 (case 3) 50 prev 20 10 5 40 15 27 th Mar 2007 30 70 65 85 80 90

Delete 50 (case 3) 40 20 10 5 70 30 15 27 th Mar 2007 65 85 80 90

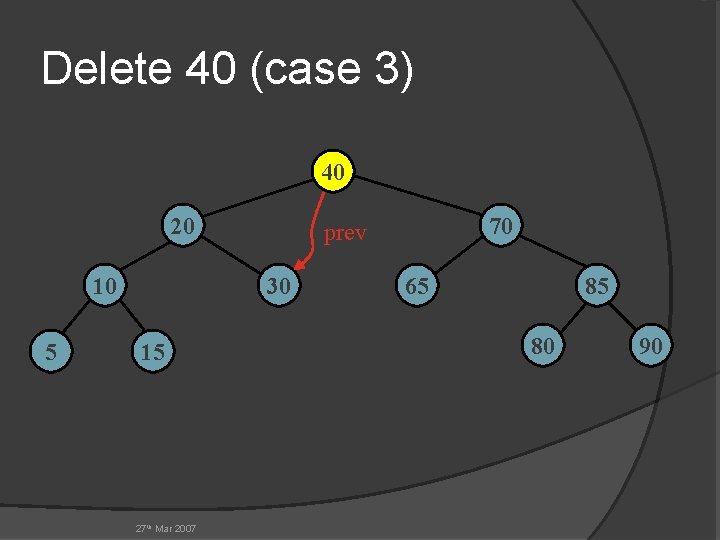
Delete 40 (case 3) 40 20 10 5 30 15 27 th Mar 2007 70 prev 65 85 80 90

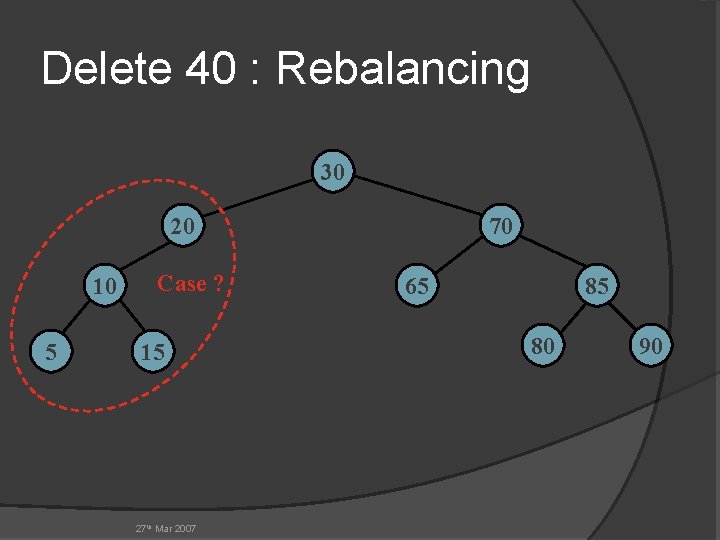
Delete 40 : Rebalancing 30 20 10 5 Case ? 15 27 th Mar 2007 70 65 85 80 90

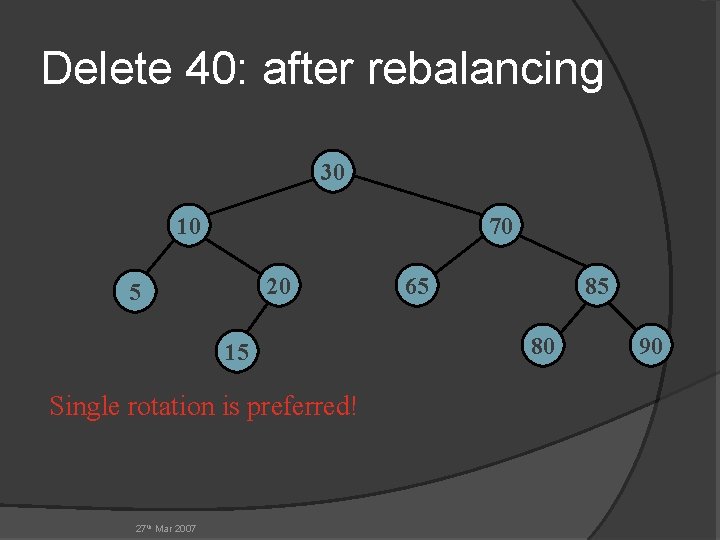
Delete 40: after rebalancing 30 10 70 20 5 15 Single rotation is preferred! 27 th Mar 2007 65 85 80 90

Minimum Element in AVL Tree � An AVL Tree of height H has at least F -1 nodes, where Fi is the i-th fibonacci number � S 0 = 1 � S 1 = 2 � SH = SH-1 + SH-2 + 1 H H-1 SH-1 27 th Mar 2007 SH-2 H+3 H-2

Summary � Find element, insert element, and remove element operations all have complexity O(log n) for worst case � Insert operation: top-down insertion and bottom up balancing 27 th Mar 2007