Average and Instantaneous Speed Learning Intention To learn

Average and Instantaneous Speed

Learning Intention: To learn the difference between average and instantaneous speed, then use this in various types of calculation. Success Criteria: Calculations involving scalars and vectors will be completed, with further maths skills such as Pythagoras and SOH-CAH-TOA to be used in future lessons.

AVERAGE SPEED The average speed is a speed measured over a large time interval. Average speed cameras are becoming more common in Scotland as they prevent drivers from simply slowing down when they see a camera. The driver must now travel at an average speed which is below the speed limit for that road.

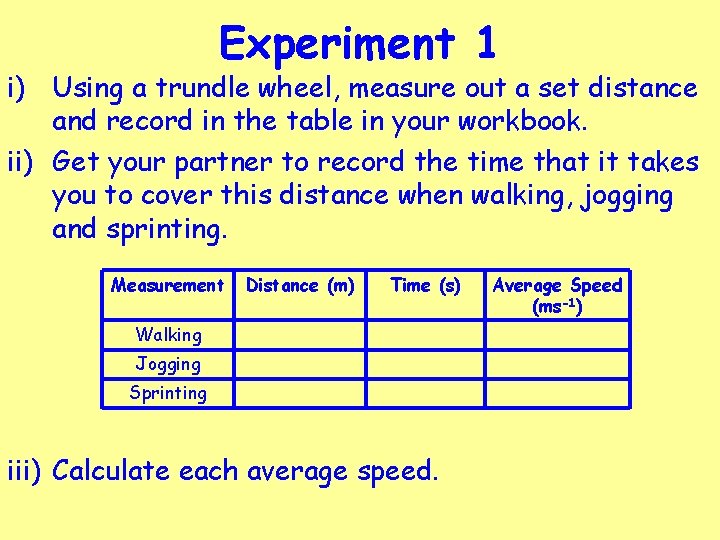
Experiment 1 i) Using a trundle wheel, measure out a set distance and record in the table in your workbook. ii) Get your partner to record the time that it takes you to cover this distance when walking, jogging and sprinting. Measurement Distance (m) Time (s) Walking Jogging Sprinting iii) Calculate each average speed. Average Speed (ms-1)

Example Now, work through this example as a class, completing the solution in your workbook: Example: Calculate the average speed of a car which travels 2400 m in 5 minutes.

AVERAGE SPEED EXPERIMENT If asked how to measure the average speed of an object (car, bicycle etc): 1. Measure the distance travelled using a metre stick (or trundle wheel). 2. Measure the time taken, with a stopclock. 3. Use the equation: d = vt. You must mention what you use to measure both of the relevant quantities.

INSTANTANEOUS SPEED Instantaneous Speed is the speed measured over a very small time interval. For example, this is what is shown on a car’s speedometer.

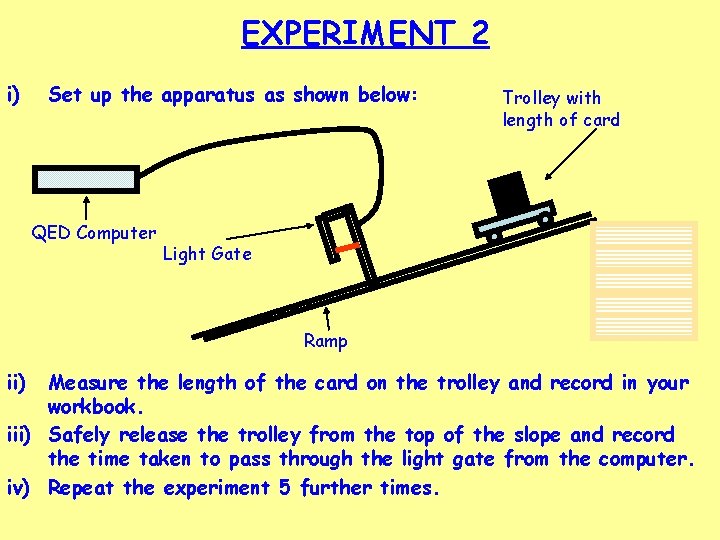
EXPERIMENT 2 i) Set up the apparatus as shown below: QED Computer Trolley with length of card Light Gate Ramp ii) Measure the length of the card on the trolley and record in your workbook. iii) Safely release the trolley from the top of the slope and record the time taken to pass through the light gate from the computer. iv) Repeat the experiment 5 further times.

EXPERIMENT v) Calculate an instantaneous speed for each time. vi) Calculate the mean instantaneous speed of the trolley. Length of Card (m) Time from Light Gate (s) Instantaneous Speed (ms-1) Mean Instantaneous Speed = ______ ms-1

Example Now, work through this example as a class, completing the solution in your workbook: Example: A car of length 4. 5 m passes through a speed trap light gate in a time of 0. 18 seconds. If the road along which the car travels is 2500 m long, calculate the car’s instantaneous speed as it passes through the trap. Now, solve the examples from your workbook in your classwork jotter showing full working for each one.

INSTANTANEOUS SPEED EXPERIMENT Instantaneous Speed is the speed measured over a very small time interval. If asked how to measure the instantaneous speed of an object (car, bicycle etc): 1. Measure the length of the card (vehicle) using a metre stick. 2. Measure the time taken, with a light gate connected to a computer. 3. Use the equation: d = vt (length of card = inst. Speed x time through light gate). You must mention what you use to measure both of the relevant quantities.

Click the picture above for a Top Gear race across several countries. i) Who has the highest average speed? ii) Who has the largest instantaneous speed? iii) What about the highest average velocity?

Success Criteria: Calculations involving scalars and vectors will be completed, with further maths skills such as Pythagoras and SOH-CAH-TOA to be used in future lessons. This success criteria can be ticked off following the Vector Diagrams lesson.

Now, use the space in your workbook to produce a summary of average and instantaneous speed. You may wish to produce concise bullet points, or draw a mind-map, or use any other useful revision technique.