Autour du Soleil de la Terre et des

Autour du Soleil, de la Terre et des noyaux de comètes Gravité à la surface l'environnement des astres Phmet-dans Observatoire de Lyon – avril: étoiles, 2014 planètes, etc

Titre un peu plus sérieux Gravitation à la surface d’un astre satellisation autour d’un corps céleste ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 2

Préambule La force due à la gravitation qui retient les objets à la surface d’un astre habituellement sphérique, s’exprime de façon simple par la loi de Newton : Si l’on applique cette force sur un objet de masse unité, on a la valeur de la gravité à la surface de ce corps appelée pesanteur sur Terre. Deux paramètres la masse du corps M et son rayon R apparaissent dans l’expression. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 3

Préambule (suite) Cette force quoique moindre s’exerce toujours en s’éloignant du corps, mais tout objet peut être satellisé si l’accélération centrifuge due à la vitesse de rotation de l’objet autour du corps compense la gravité L’expression de la vitesse de satellisation à une distance d du centre est donnée par la formule : qui s’obtient facilement en égalant l’accélération centrifuge due à la rotation, à la pesanteur : A une certaine vitesse, l’objet se libère de sa tutelle gravitationnelle. Cette vitesse, à la surface de l’astre est : ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 4

Préambule (fin) Lorsque l’objet est satellisé, les lois de Kepler sont toutes applicables et permettent d’avoir les caractéristiques des orbites : période, demi-grand axe, etc. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 5

Gravité à la surface La valeur de la gravité g à la surface de la Terre est bien connue, facile à retrouver connaissant son diamètre et sa masse. Il en est de même de la plupart des objets du système solaire. Ces calculs peuvent faire l’objets de nombreux exercices qui présentent un intérêt pratique pour comprendre les conditions qui règnent à la surface des astres. Les vitesse de libération sont des données essentielles dans le cas des sondes à envoyer vers leur cible. Elles sont aussi capitales pour comprendre l’évolution des atmosphères des planètes. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 6

Gravité à la surface La température à la surface d’un astre conditionne la vitesse d’agitation moyenne des particules gazeuses. Si celle-ci est proche de la vitesse de libération, il est facile de comprendre la présence d’atmosphère ou sa perte, ou encore l’évaporation sélective des gaz plus légers. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 7

Travail et calculs Pour faire les calculs avec ces formules, on peut faire appel à un tableur dans lequel on rentre toutes les caractéristiques différents corps. Comme les masses, les rayons peuvent varier dans des proportions importantes, avoir des variables continues est une facilité. Geogebra nous donne cette commodité par l’utilisation de curseurs afin de faire varier R et M et obtenir : - gravité à la surface d’un corps - vitesse de satellisation à la surface - vitesse et période de satellisation à la distance d - vitesse d’évasion à la surface Pour parler d’actualité, nous regarderons ce qui va se passer lors de la rencontre de la sonde Rosetta avec la comète 67 P/Churyumov–Gerasimenko. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 8

Travail et calculs Remarques sur la façon de procéder Les noms des variables utilisés ne sont pas imposés. La commodité de lecture et de construction conseille de les garder tels quels. Ce document et le texte accompagnateur permet de construire le TD pas à pas Les textes en gras et en police Arial sont les variables et les expressions à rentrer et utiliser dans Geogebra avec la syntaxe telle qu’elle est écrite. La construction des objets et équation n’est pas absolu. Geogebra permet souvent de construire les mêmes objets par des procédés différents. A vous de choisir ce qui vous convient. Penser à sauvegarder régulièrement. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 9

Travail et calculs Cette icône indique un travail avec Geogebra : Pour les personnes qui débutent dans Geogebra vous pouvez consulter le fichier elements_geogebra. pdf téléchargeable à la page et les fichiers accompagnateurs : http: //cral. univ-lyon 1. fr/labo/fc/cdroms/cdrom 2013/Lumetexo/index. html construit comme initiation à Geogebra. Pour les personnes qui débutent dans Geogebra vous pouvez consulter le fichier elements_geogebra. pdf téléchargeable à : cral. univ-lyon 1. fr/labo/fc/cdroms/cdrom 2014/gravitation/elements_geogebra. pdf. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 10

Calculs gravitationnels ► Ouvrir Geogebra 2 D ► Charger le fichier astro_data. ggb Dans la fenêtre de saisie rentrer la valeur de G : G = 6. 6738 * 10^-11 De l’unité astronomique (en km) ua : ua = 150000000 Dans la partie Tableur de ce fichier sont données pour information, les rayons et masses des principaux corps du système solaire. Valeurs prises sur le site de l’IMCCE www. imcce. fr Pour calculer les paramètres gravitationnels des différents objets on utilisera les valeurs de leurs masses et leurs rayons que l’on prendra dans le tableur. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 11

Illustrations Le système solaire ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 12

Illustrations Dimensions d’étoiles http: //www. jmmasuy. net http: //www. astrosurf. com http: //www. sciencesetavenir. fr Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc ► 13

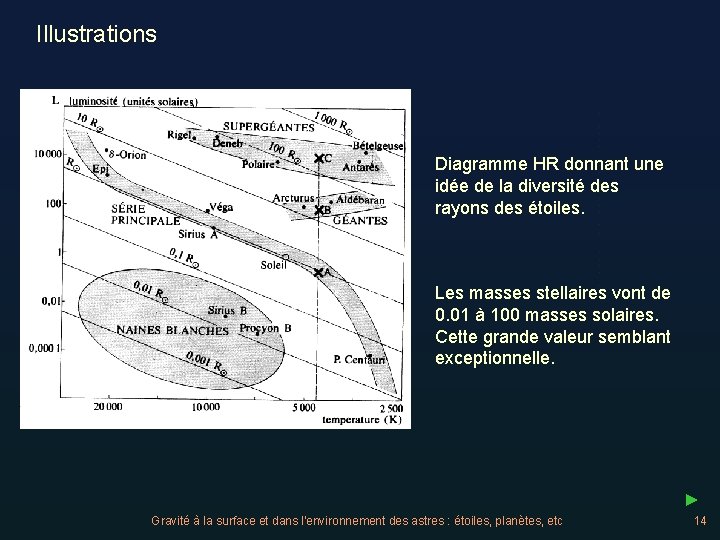
Illustrations Diagramme HR donnant une idée de la diversité des rayons des étoiles. Les masses stellaires vont de 0. 01 à 100 masses solaires. Cette grande valeur semblant exceptionnelle. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 14

Curseurs La création de curseurs variant de façon continue simplifiera la manipulation de ces valeurs. Il suffira d’ajuster les curseurs sur les valeurs des rayons et masses du corps trouvées dans la partie tableur. Curseur double Un curseur simple n’est pas adapté à ces calculs parce que l’étendue des plages de valeurs peut être très grande. Exemple : l’étendue des masses allant de 7. 34 1022 kg pour la Lune à 2 1029 kg pour le Soleil et plus. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 15

Curseurs On vient donc d’utiliser la notation scientifique. Comment l’adapter aux curseurs ? Curseur double Pour palier cette difficulté, on scinde chaque curseur en deux : • un pour les chiffres significatifs • un deuxième pour les puissances de dix. Une variable ( R pour le rayon et M pour la masse) fait la synthèse de ces curseurs. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 16

Curseurs ► Création des variables par M et R quatre curseurs Variable Objet Curseur Plage incrément Masse M = curs_M*10^curs 10_M curs_M 0 – 10 0. 01 curs 10_M 0 - 40 1 curs_R 0 - 10 0. 01 curs 10_R 0 -9 1 Rayon R = curs_R*10^curs 10_R Sauvegarder en donnant un nouveau nom personnalisé. Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc ► 17

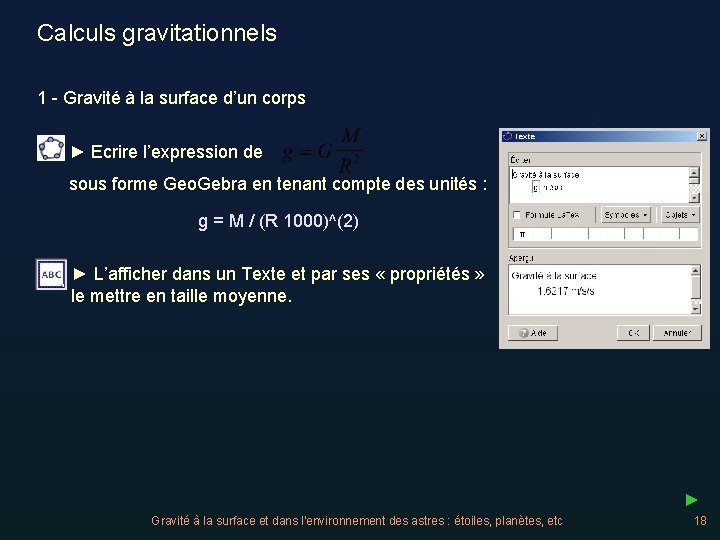
Calculs gravitationnels 1 - Gravité à la surface d’un corps ► Ecrire l’expression de sous forme Geo. Gebra en tenant compte des unités : g = M / (R 1000)^(2) ► L’afficher dans un Texte et par ses « propriétés » le mettre en taille moyenne. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 18

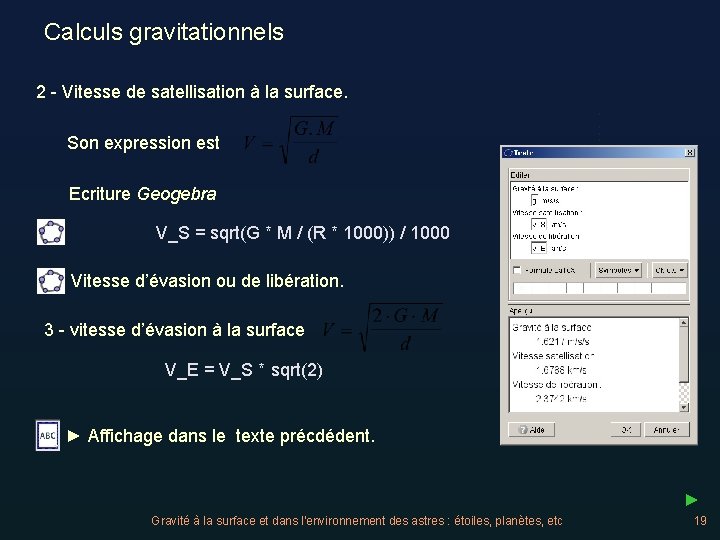
Calculs gravitationnels 2 - Vitesse de satellisation à la surface. Son expression est Ecriture Geogebra V_S = sqrt(G * M / (R * 1000)) / 1000 Vitesse d’évasion ou de libération. 3 - vitesse d’évasion à la surface V_E = V_S * sqrt(2) ► Affichage dans le texte précdédent. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 19

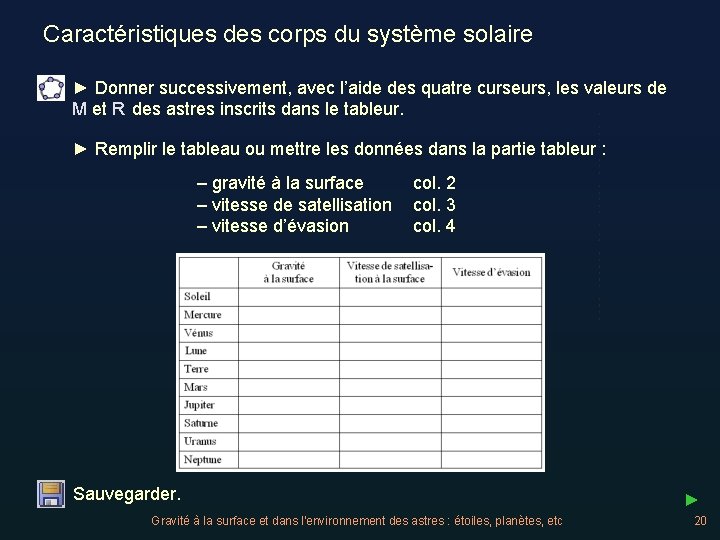
Caractéristiques des corps du système solaire ► Donner successivement, avec l’aide des quatre curseurs, les valeurs de M et R des astres inscrits dans le tableur. ► Remplir le tableau ou mettre les données dans la partie tableur : – gravité à la surface – vitesse de satellisation – vitesse d’évasion col. 2 col. 3 col. 4 Sauvegarder. Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc ► 20

Satellisation à la distance a ► Construire une variable a avec deux curseurs curs_a et curs 10_a comme précédemment qui permettra de mettre un satellite en orbite circulaire à la distance a du centre de l’objet. Valeur exprimée en kilomètres. Plage de variations : de quelques km à plusieurs unités astronomiques. ► Calculer : - la gravité à cette distance - la période de rotation - la vitesse sur l’orbite. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 21

Satellisation à la distance a ► La force de gravité ga à la distance g_a = G * M / (a * 1000)^(2) ► La période de rotation Le demi-grand axe vaut donc a et sa période P s’exprime à partir de la 3ème loi de Kepler en négligeant la masse de l’objet : Soit : P = sqrt( 4 * π^2 / G * (a * 1000)^3 / M ) ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 22

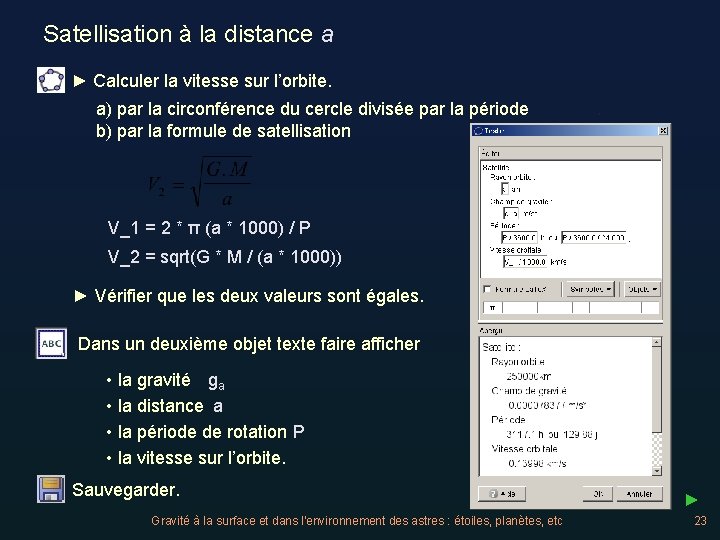
Satellisation à la distance a ► Calculer la vitesse sur l’orbite. a) par la circonférence du cercle divisée par la période b) par la formule de satellisation V_1 = 2 * π (a * 1000) / P V_2 = sqrt(G * M / (a * 1000)) ► Vérifier que les deux valeurs sont égales. Dans un deuxième objet texte faire afficher • la gravité ga • la distance a • la période de rotation P • la vitesse sur l’orbite. Sauvegarder. Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc ► 23

Satellisation à la distance a On peut donc simuler tous les corps en orbites : - satellites autour de la terre - la Lune - les planètes du système solaire, etc. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 24

La sonde Rosetta Projet ambitieux, la sonde Rosetta doit accompagner le noyau de la comète 67 P/Churyumov–Gerasimenko. La mission comporte deux volets : a) satelliser la sonde autour du noyau pour l’observer et suivre son dégazage et dépoussiérage lors de son passage au périhélie prévu pour le 13 août 2015. b) faire atterrir un petit engin (Philae) sur le sol même du noyau pour l’étude du sol. Le problème principal de la satellisation est l’extrême faiblesse de l’amplitude de la force gravitationnelle qui va lier les deux corps. Avec notre programme Geogebra universel, nous allons faire une simulation des conditions de pesanteur dans lesquelles va plonger la sonde Rosetta. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 25

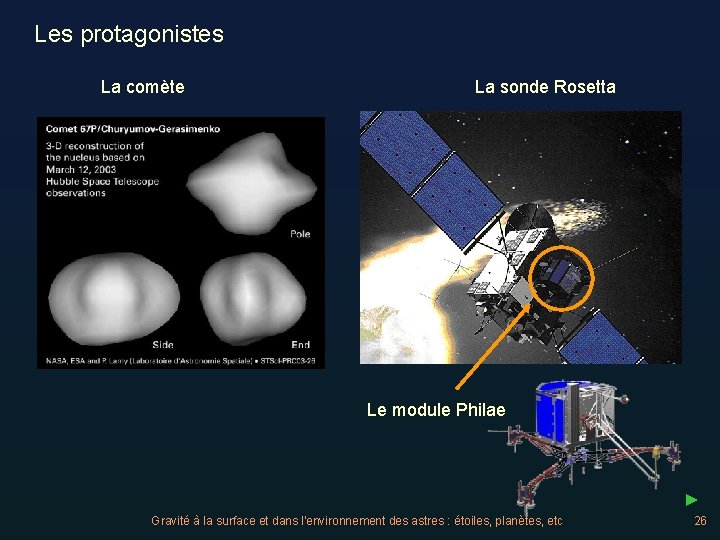
Les protagonistes La comète La sonde Rosetta Le module Philae ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 26

Le noyau de la comète Les observations actuelle donnent : - dimensions : corps non sphérique approximativement de 5 km sur 3 km. - estimations de sa masse volumique : de 100 à 370 kg / m 3 - période de rotation 17. 3 heures environ ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 27

Le noyau de la comète Masse du noyau Pour faire les calculs de gravité, il faut une masse estimée du noyau. On simplifie le problème, en assimilant le noyau de la comète à un ellipsoïde de révolution : - grand axe 2 a. C = 5 km - petit axe 2 b. C = 3 km. Volume : et si sa masse volumique est r, sa masse totale sera : On prendra une masse volumique de 100 kg M / m 3 ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 28

Le noyau de la comète ► dans Geogebra : a_c = 2. 5 b_c = 1. 5 V_{comete} = 4 / 3 π * a_c * 1000 (b_c * 1000)^2 M_{comète} = V_{comète} * 100 ► Donner la gravité à sa surface et comparer la à celle de la Terre Masse volumique r = 100 kg/m 3 Grand axe Petit axe r = 370 kg/m 3 Grand axe Petit axe Gravité Comète Rap. Terre/comète ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 29

Satellisation de la sonde La sonde devrait être satellisée à environ 25 km. ► Calculer la force de gravité exercée par le noyau sur la sonde, sa période de rotation et sa vitesse sur son orbite. ► Faire le même calcul au cas ou la sonde aurait été satellisée juste au dessus de la surface du noyau de la comète. a = 25 km a = 3 km Force de gravité exercée par le noyau Période de rotation Vitesse sur son orbite ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 30

Satellisation de la sonde La période de rotation de la comète sur elle-même est de 12. 7 heures environ. ► Trouver à quelle distance devrait-elle être placée pour avoir une orbite “géostationnaire” ? ► Autre question et calcul : Sous quel angle la sonde voit-elle le noyau ? Comparer au diamètre angulaire de la Lune vue de la Terre. Pour la dernière fois SAUVEGARDER. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 31

Calcul complémentaire Sous quel diamètre la sonde voit-on le noyau de la comète ? Voir le fichier : diametre_angulaire_noyau. ggb La sonde est placée à une distance variable grâce à un curseur dist. De ce point on construit les deux tangentes au cercle représentant la dimension la plus grande de l’ellipsoïde noyau. L’angle cherché est l’angle des deux droites. ► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 32

► Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 33

Nucleus properties of Comet 67 P/Churyumov–Gerasimenko estimated from non-gravitational force modeling Icarus Volume 176, Issue 2, August 2005, Pages 453– 477 Abstract By considering model comet nuclei with a wide range of sizes, prolate ellipsoidal shapes, spin axis orientations, and surface activity patterns, constraints have been placed on the nucleus properties of the primary Rosetta target, Comet 67 P/Churyumov–Gerasimenko. This is done by requiring that the model bodies simultaneously reproduce the empirical nucleus rotational lightcurve, the water production rate as function of time, and non-gravitational changes (per apparition) of the orbital period (ΔPΔP), longitude of perihelion (Δϖ), and longitude of the ascending node (ΔΩ). Two different thermophysical models are used in order to calculate the water production rate and non-gravitational force vector due to nucleus outgassing of the model objects. By requiring that the nominal water production rate measurements are reproduced as well as possible, we find that the semi-major axis of the nucleus is close to 2. 5 km, the nucleus axis ratio is approximately 1. 4, while the spin axis argument is either 60°± 15° or 240°± 15°. The spin axis obliquity can only be preliminarily constrained, indicating retrograde rotation for the first argument value, and prograde rotation for the second suggested spin axis argument. A nucleus bulk density in the range 100– 370 kg m− 3 is found for the nominal ΔPΔP, while an upper limit of 500 kg m− 3 can be placed if the uncertainty in ΔPΔP is considered. Both considered thermophysical models yield the same spin axis, size, shape, and density estimates. Alternatively, if calculated water production rates within an envelope around the measured data are considered, it is no longer possible to constrain the size, shape, and spin axis orientation of the nucleus, but an upper limit on the nucleus bulk density of 600 kg m− 3 is suggested. Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc ► 34

Orbite de la comète 67 P/Churyumov–Gerasimenko L’orbite d’une planète, astéroïde ou comète se définit par rapport au plan de l’écliptique par des paramètres. Voir glossaire de l’IMCCE : http: //www. imcce. fr/langues/fr/grandpublic/systeme/promenade/pages 2/221. html Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 35

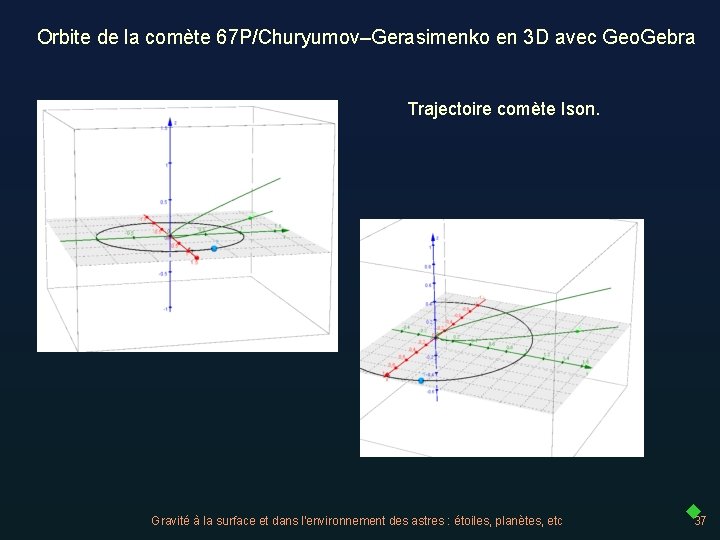
Orbite de la comète 67 P/Churyumov–Gerasimenko en 3 D avec Geo. Gebra Le tracé en 3 dimensions de la trajectoire de la comète et l’orbite de la Terre peut être fait avec Geogebra 3 D sur la période du passage au périhélie. Cet exercice a été fait à l’identique pour la comète ISON fin 2013. Les fichiers du TD (explications et Geogebra) sont à la page de la Formation Continue : http: //cral. univ-lyon 1. fr/labo/fc/cdroms/cdrom 2014/astrobases/index. html Les éphémérides de la comète sont à trouver en ligne à la page de l’IMCCE : http: //www. imcce. fr/fr/ephemerides/formulaire/form_ephepos. php avec la désignation : P/Churyumov-Gerasimenko Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 36

Orbite de la comète 67 P/Churyumov–Gerasimenko en 3 D avec Geo. Gebra Trajectoire comète Ison. Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 37

FIN Gravité à la surface et dans l'environnement des astres : étoiles, planètes, etc 38