Autonomous InterTask Transfer in Reinforcement Learning Domains Matthew

Autonomous Inter-Task Transfer in Reinforcement Learning Domains Matthew E. Taylor Learning Agents Research Group Department of Computer Sciences University of Texas at Austin 6/24/2008 Matthew E. Taylor 1

Inter-Task Transfer • Learning tabula rasa can be unnecessarily slow • Humans can use past information – • Soccer with different numbers of players Agents leverage learned knowledge in novel tasks Matthew E. Taylor 2

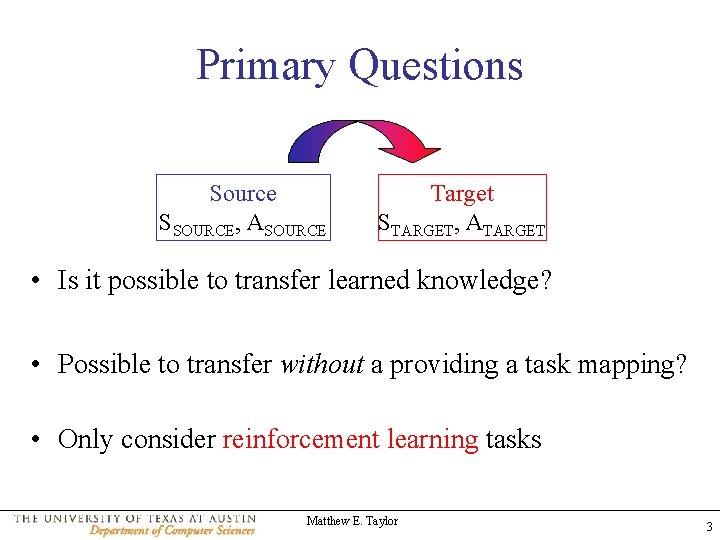
Primary Questions Source SSOURCE, ASOURCE Target STARGET, ATARGET • Is it possible to transfer learned knowledge? • Possible to transfer without a providing a task mapping? • Only consider reinforcement learning tasks Matthew E. Taylor 3

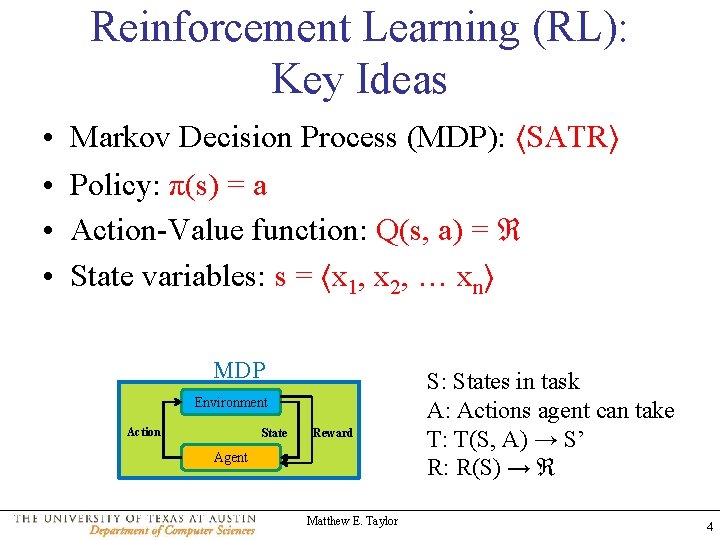
Reinforcement Learning (RL): Key Ideas • • Markov Decision Process (MDP): ⟨SATR⟩ Policy: π(s) = a Action-Value function: Q(s, a) = ℜ State variables: s = ⟨x 1, x 2, … xn⟩ MDP Environment Action State Reward Agent Matthew E. Taylor S: States in task A: Actions agent can take T: T(S, A) → S’ R: R(S) → ℜ 4

Outline • • • Reinforcement Learning Background Inter-Task Mappings Value Function Transfer MASTER: Learning Inter-Task Mappings Related Work Future Work and Conclusion Matthew E. Taylor 5

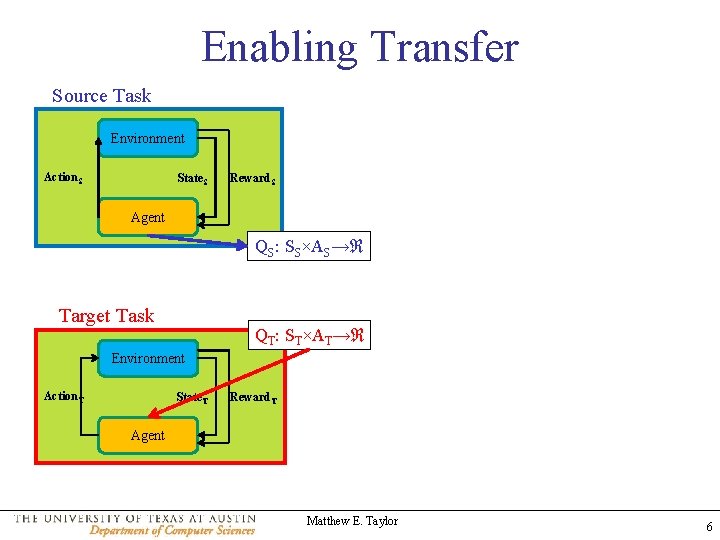
Enabling Transfer Source Task Environment Action. S State. S Reward. S Agent QS: SS×AS→ℜ Target Task QT: ST×AT→ℜ Environment Action. T State. T Reward. T Agent Matthew E. Taylor 6

Inter-Task Mappings Source Target Source Matthew E. Taylor Target 7

Inter-Task Mappings • χx: starget→ssource – Given state variable in target task (some x from s=x 1, x 2, … xn) – Return corresponding state variable in source task Target Source ASOURCE χx χA ⟨x 1…xn⟩ {a 1…am} SSOURCE – Similar, but for actions ⟨x 1…xk⟩ {a 1…aj} • χA: atarget→asource STARGET A TARGET • Intuitive mappings exist in some domains (Oracle) • Used to construct transfer functional Matthew E. Taylor 8

Keepaway [Stone, Sutton, and Kuhlmann 2005] Goal: Maintain possession of ball K 2 K 1 5 agents 3 (stochastic) actions 13 (noisy & continuous) state variables T 1 K 3 T 2 Keeper with ball may hold ball or pass to either teammate 4 vs. 3: Both takers move 7 agents towards player with ball 4 actions 19 state variables Matthew E. Taylor

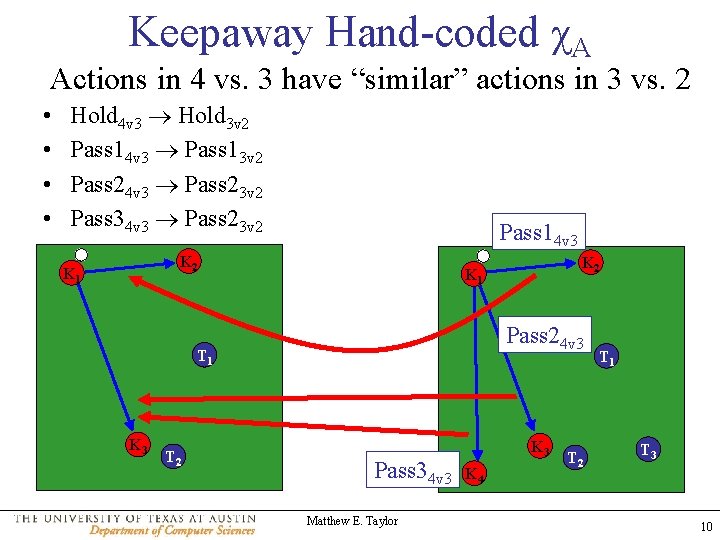
Keepaway Hand-coded χA Actions in 4 vs. 3 have “similar” actions in 3 vs. 2 • • Hold 4 v 3 Hold 3 v 2 Pass 14 v 3 Pass 13 v 2 Pass 24 v 3 Pass 23 v 2 Pass 34 v 3 Pass 23 v 2 Pass 14 v 3 K 2 K 1 Pass 24 v 3 T 1 K 3 T 2 K 1 Pass 34 v 3 Matthew E. Taylor K 3 K 4 T 2 T 1 T 3 10

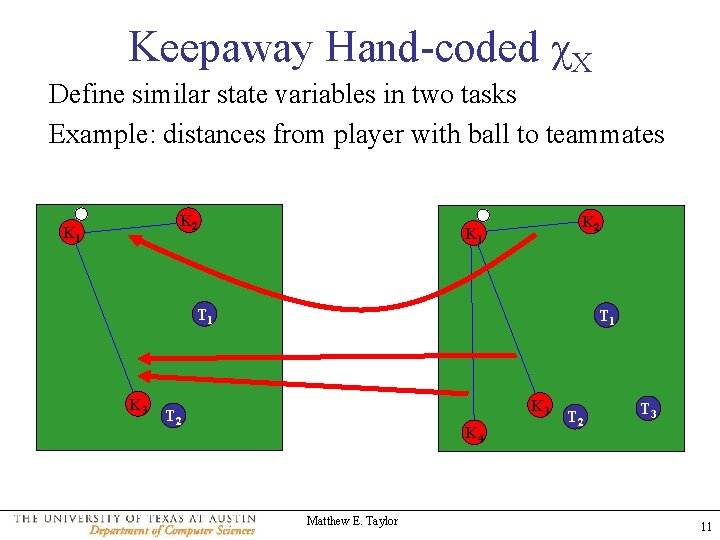
Keepaway Hand-coded χX Define similar state variables in two tasks Example: distances from player with ball to teammates K 2 K 1 T 1 K 3 T 2 K 4 Matthew E. Taylor T 2 T 3 11

Outline • • • Reinforcement Learning Background Inter-Task Mappings Value Function Transfer MASTER: Learning Inter-Task Mappings Related Work Future Work and Conclusion Matthew E. Taylor 12

Value Function Transfer Source Target SSOURCE, ASOURCE STARGET, ATARGET Matthew E. Taylor 13

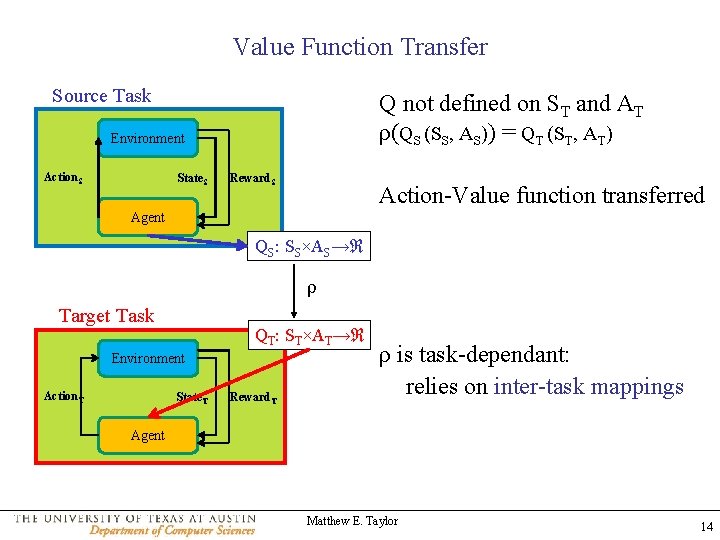
Value Function Transfer Source Task Q not defined on ST and AT ρ(QS (SS, AS)) = QT (ST, AT) Environment Action. S State. S Reward. S Action-Value function transferred Agent QS: SS×AS→ℜ ρ Target Task QT: ST×AT→ℜ Environment Action. T State. T Reward. T ρ is task-dependant: relies on inter-task mappings Agent Matthew E. Taylor 14

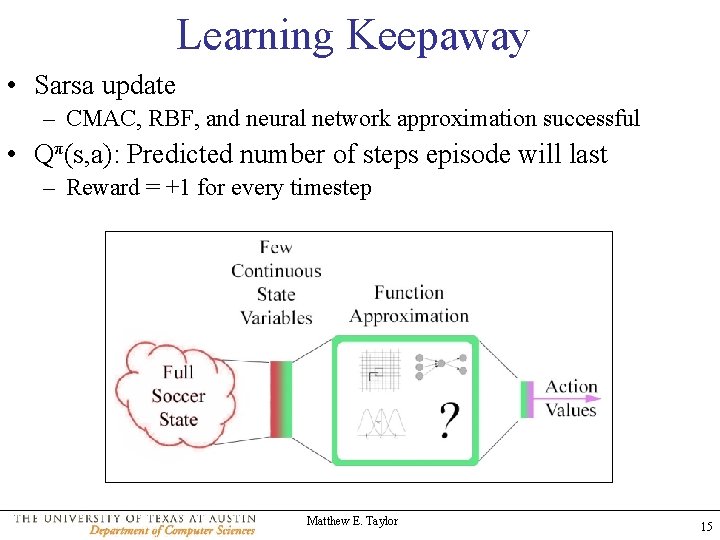
Learning Keepaway • Sarsa update – CMAC, RBF, and neural network approximation successful • Qπ(s, a): Predicted number of steps episode will last – Reward = +1 for every timestep Matthew E. Taylor 15

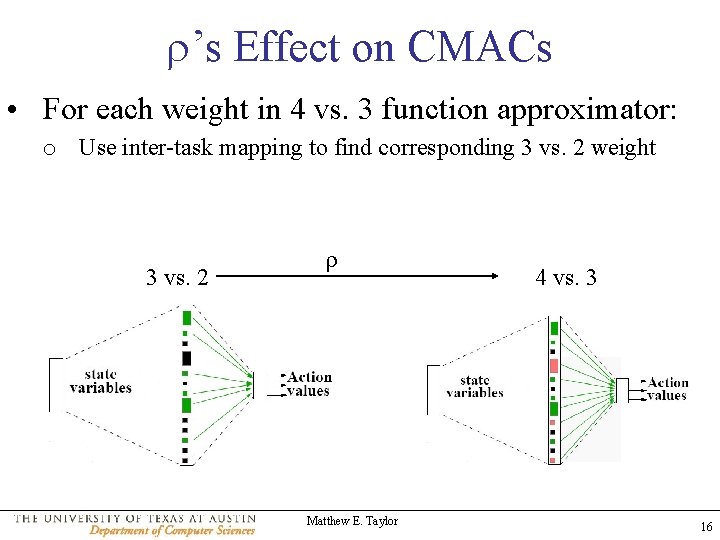
’s Effect on CMACs • For each weight in 4 vs. 3 function approximator: o Use inter-task mapping to find corresponding 3 vs. 2 weight 3 vs. 2 Matthew E. Taylor 4 vs. 3 16

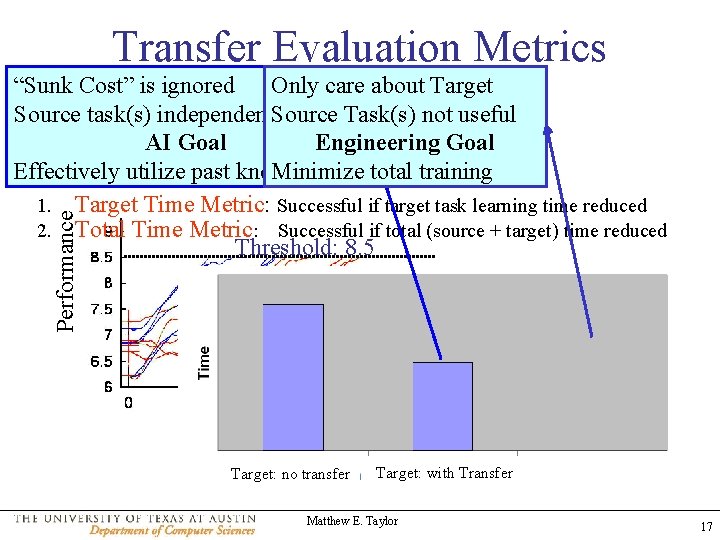
Transfer Evaluation Metrics Performance “Sunk is ignored Only care about Target Set a. Cost” threshold performance Source. Majority task(s)ofindependently Source useful Task(s) agents can achieve with learningnot useful AI Goal Engineering Goal Effectively utilize past knowledge Minimize total training Two distinct scenarios: 1. Target Time Metric: Successful if target task learning time reduced 2. Total Time Metric: Successful if total (source + target) time reduced Threshold: 8. 5 Target: no Transfer Target: no transfer Target: with Transfer Matthew E. Taylor Target + Source: with Transfer 17

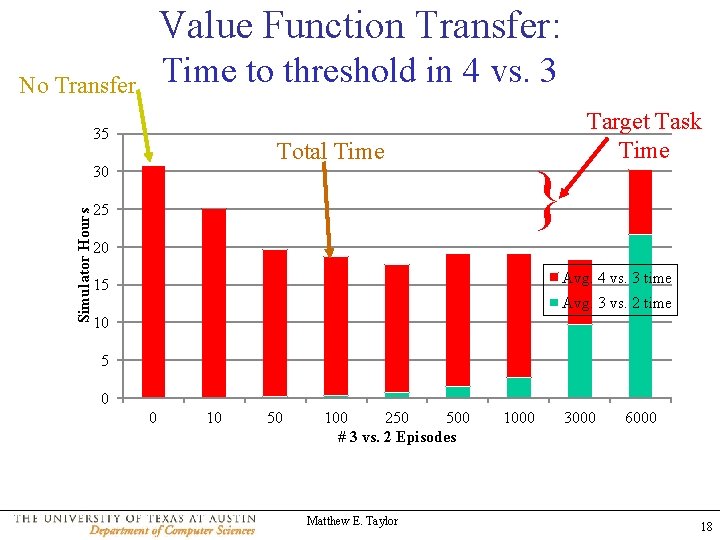
Value Function Transfer: Time to threshold in 4 vs. 3 No Transfer 35 Total Time Simulator Hours 30 25 } Target Task Time 20 Avg. 4 vs. 3 time 15 Avg. 3 vs. 2 time 10 5 0 0 10 50 100 250 500 # 3 vs. 2 Episodes Matthew E. Taylor 1000 3000 6000 18

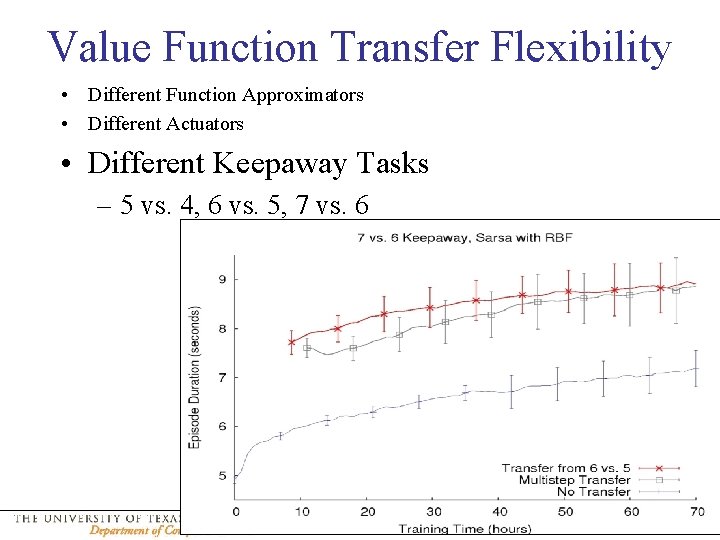
Value Function Transfer Flexibility • Different Function Approximators – Radial Basis Function & Neural Network • Different Actuators Pass accuracy • “Accurate” passers have normal actuators • “Inaccurate” passers have less capable kick actuators Value Function Transfer also reduces target task time and total time: • Inaccurate 3 vs. 2 → Inaccurate 4 vs. 3 • Accurate 3 vs. 2 → Inaccurate 4 vs. 3 • Inaccurate 3 vs. 2 → Accurate 4 vs. 3 Matthew E. Taylor 19

Value Function Transfer Flexibility • Different Function Approximators • Different Actuators • Different Keepaway Tasks – 5 vs. 4, 6 vs. 5, 7 vs. 6 Matthew E. Taylor 20

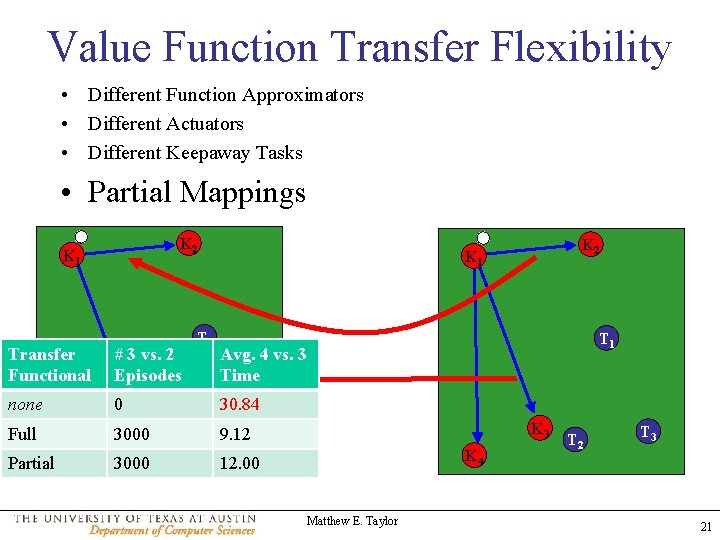
Value Function Transfer Flexibility • Different Function Approximators • Different Actuators • Different Keepaway Tasks • Partial Mappings K 2 K 1 Transfer Functional # 3 vs. 2 Episodes none 0 30. 84 Full K 3 3000 T 2 3000 9. 12 Partial K 2 K 1 T 1 Avg. 4 vs. 3 Time K 3 K 4 12. 00 Matthew E. Taylor T 2 T 3 21

Value Function Transfer Flexibility • • Different Function Approximators Different Actuators Different Keepaway Tasks Partial Mappings • Different Domains – Knight Joust to 4 vs. 3 Keepaway Opponent moves directly towards player # Knight Joust 4 vs. 3 Episodes Goal: Travel from start Time to goal line 0 30. 84 2 agents 24. 24 325, 000 actions 350, 000 state variables 18. 90 Fully Observable Player may move Discrete State Space (Q-table with ~600 s, a pairs) North, or take a knight. Deterministic Actions jump to either side Matthew E. Taylor 22

Value Function Transfer Flexibility • • Different Function Approximators Different Actuators Different Keepaway Tasks Partial Mappings • Different Domains – Knight Joust to 4 vs. 3 Keepaway – 3 vs. 2 Flat Reward, 3 vs. 2 Giveaway Source Task Episodes None 3 vs. 2 Keepaway 4 vs. 3 Time 30. 84 3000 9. 12 3 vs. 2 Flat Reward 3000 19. 42 3 vs. 2 Giveaway 32. 94 3000 Matthew E. Taylor 23

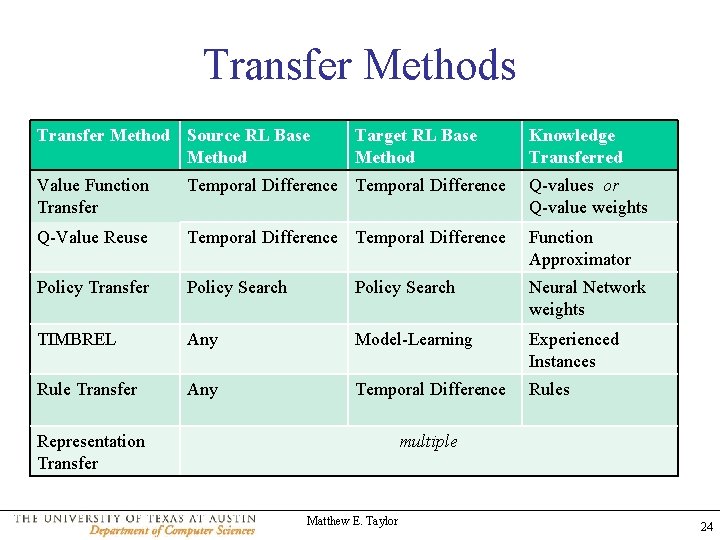
Transfer Methods Transfer Method Source RL Base Method Target RL Base Method Knowledge Transferred Value Function Transfer Temporal Difference Q-values or Q-value weights Q-Value Reuse Temporal Difference Function Approximator Policy Transfer Policy Search Neural Network weights TIMBREL Any Model-Learning Experienced Instances Rule Transfer Any Temporal Difference Rules Representation Transfer multiple Matthew E. Taylor 24

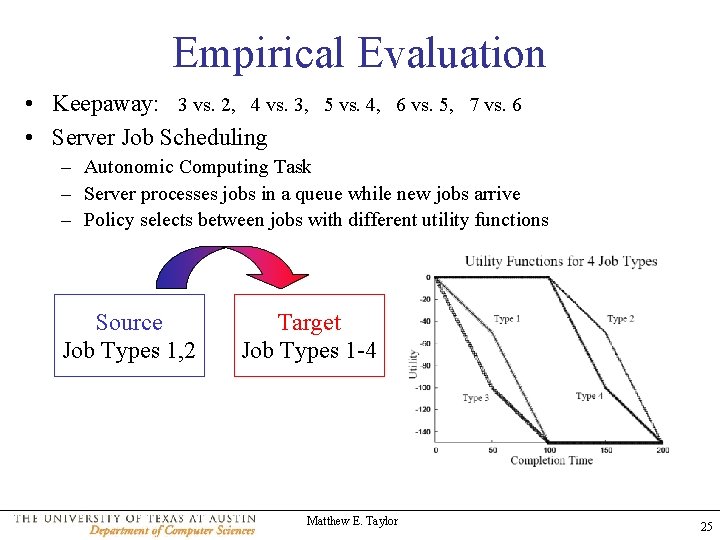
Empirical Evaluation • Keepaway: 3 vs. 2, 4 vs. 3, 5 vs. 4, 6 vs. 5, 7 vs. 6 • Server Job Scheduling – Autonomic Computing Task – Server processes jobs in a queue while new jobs arrive – Policy selects between jobs with different utility functions Source Job Types 1, 2 Target Job Types 1 -4 Matthew E. Taylor 25

Empirical Evaluation • Keepaway: 3 vs. 2, 4 vs. 3, 5 vs. 4, 6 vs. 5, 7 vs. 6 • Server Job Scheduling – Autonomic Computing Task – Server processes jobs in a queue while new jobs arrive – Policy selects between jobs with different utility functions • Mountain Car – 2 D – 3 D • Cross-Domain Transfer – Ringworld to Keepaway – Knight’s Joust to Keepaway # Actions K # State Variables. K Discrete vs. Continuous T Deterministic vs. Stochastic Fully vs. Partially Observable K T Single Agent vs. Multi-Agent 2 1 1 3 Matthew E. Taylor 2

Outline • • • Reinforcement Learning Background Inter-Task Mappings Value Function Transfer MASTER: Learning Inter-Task Mappings Related Work Future Work and Conclusion Matthew E. Taylor 27

Learning Task Relationships • • • Sometimes task relationships are unknown Necessary for Autonomous Transfer But finding similarities (analogies) can be very hard! Key idea: – Agents may generate data (experience) in both tasks – Leverage existing machine learning techniques 2 Techniques, differ in amount of background knowledge Matthew E. Taylor 28

Context • Steps to enable Autonomous transfer: 1. 2. 3. Select a relevant source task, given a target task Learn how the source and target tasks are related Effectively transfer knowledge between tasks ? • Transfer is Feasible (step 3) • Steps toward Finding Mappings between Tasks (step 2) – Leverage full QDBNs to search for mappings [Liu and Stone, 2006] – Test possible mappings on-line [Soni and Singh, 2006] – Mapping Learning via Classification Matthew E. Taylor 29

Context • Steps to enable Autonomous transfer: 1. Select a relevant source task, given a target task Source Target 2. Learn how the source and target tasks are related 3. S, Effectively tasks A, r, S’ transfer knowledge. S, between A, r, S’ A • Transfer is Feasible (step 3) A →A S, r, S’ • Steps toward Finding Mappings between Tasks (step 2) Action Classifier – Leverage full QDBNs to search for mappings [Liu and Stone, 2006] – Test possible mappings on-line [Soni and Singh, 2006] – Mapping Learning via Classification Matthew E. Taylor 30

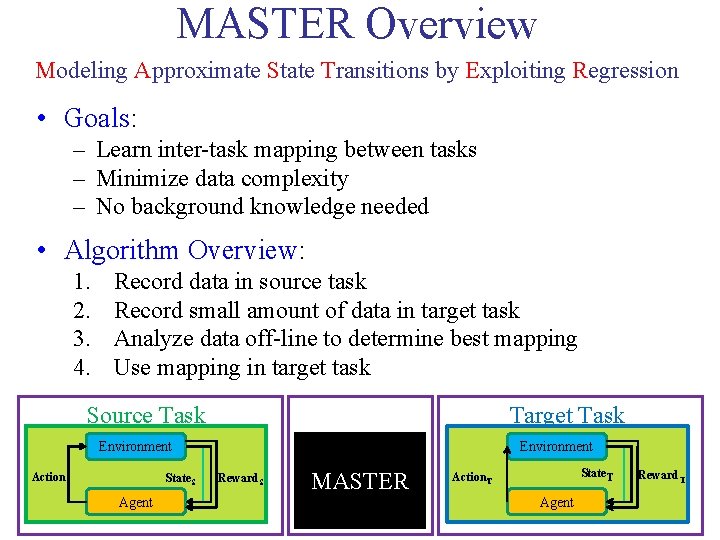
MASTER Overview Modeling Approximate State Transitions by Exploiting Regression • Goals: – Learn inter-task mapping between tasks – Minimize data complexity – No background knowledge needed • Algorithm Overview: 1. 2. 3. 4. Record data in source task Record small amount of data in target task Analyze data off-line to determine best mapping Use mapping in target task Source Task Target Task Environment Action. S State. S Environment Reward. S MASTER State. T Action. T Agent Matthew E. Taylor Reward. T

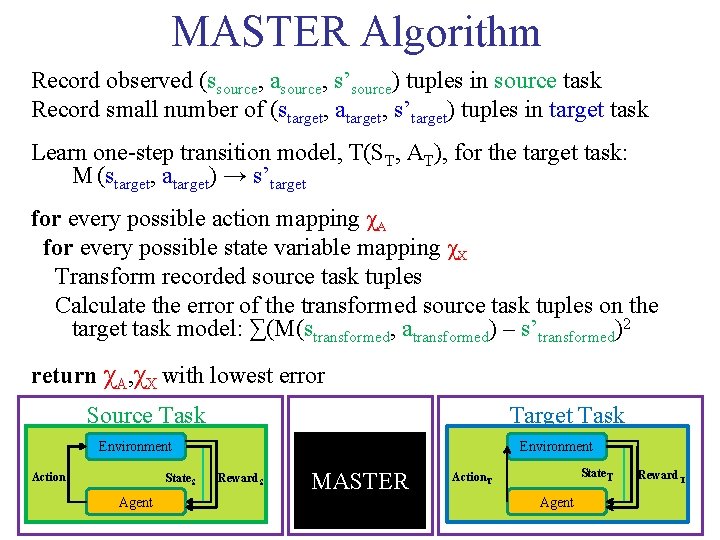
MASTER Algorithm Record observed (ssource, asource, s’source) tuples in source task Record small number of (starget, atarget, s’target) tuples in target task Learn one-step transition model, T(ST, AT), for the target task: M (starget, atarget) → s’target for every possible action mapping χA for every possible state variable mapping χX Transform recorded source task tuples Calculate the error of the transformed source task tuples on the target task model: ∑(M(stransformed, atransformed) – s’transformed)2 return χA, χX with lowest error Source Task Target Task Environment Action. S State. S Environment Reward. S MASTER State. T Action. T Agent Matthew E. Taylor Reward. T

Observations • Pros: • Very little target task data needed (sample complexity) • Analysis for discovering mappings is off-line • Cons: • Exponential in # of state variables and actions Matthew E. Taylor 33

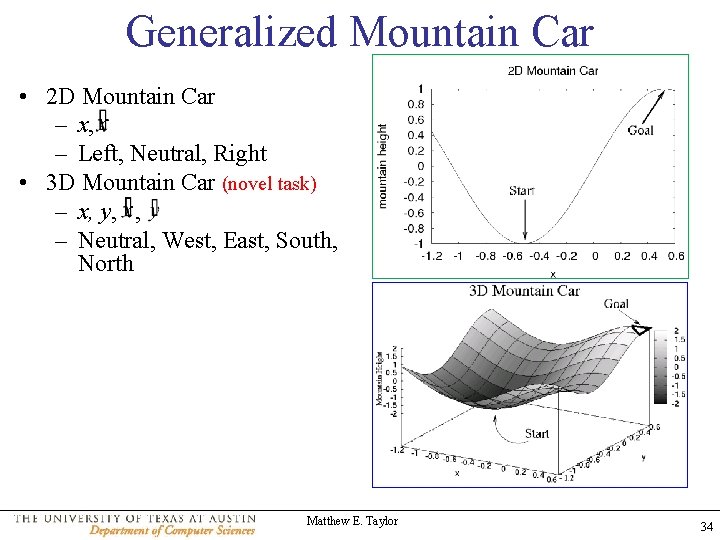
Generalized Mountain Car • 2 D Mountain Car – x, – Left, Neutral, Right • 3 D Mountain Car (novel task) – x, y, , – Neutral, West, East, South, North Matthew E. Taylor 34

Generalized Mountain Car • 2 D Mountain Car – x, – Left, Neutral, Right • 3 D Mountain Car (novel task) – x, y, , – Neutral, West, East, South, North Both tasks: • Episodic • Scaled State Variables • Sarsa • CMAC function approximation • χX – x, y → x – , → • χA – Neutral → Neutral – West, South → Left – East, North → Right Matthew E. Taylor 35

MASTER Algorithm Record observed (ssource, asource, s’source) tuples in source task Record small number of (starget, atarget, s’target) tuples in target task Learn one-step transition model, T(S, A), for the target task: M (starget, atarget) → s’target for every possible action mapping χA for every possible state variable mapping χX Transform recorded source task tuples Calculate the error of the transformed source task tuples on the target task model: ∑(M(stransformed, atransformed) – s’ transformed)2 return χA, χX with lowest error Matthew E. Taylor 36

MASTER and Mountain Car Record observed (x, , a 2 D, x’, ’) tuples in 2 D task Record small number of (x, y, , , a 3 D, x’, y’, ’, ’) tuples in 3 D task Learn one-step transition model, T(S, A), for the 3 D task: M (x, y, , , a 3 D) →x’, y’, ’, ’ for every possible action mapping χA for every possible state variable mapping χX Transform recorded source task tuples Calculate the error of the transformed source task tuples on the target task model: ∑(M(stransformed, atransformed) – s’ transformed)2 return χA, χX with lowest error (of 240 possible mappings: 16 state variables × 15 actions) Matthew E. Taylor 39

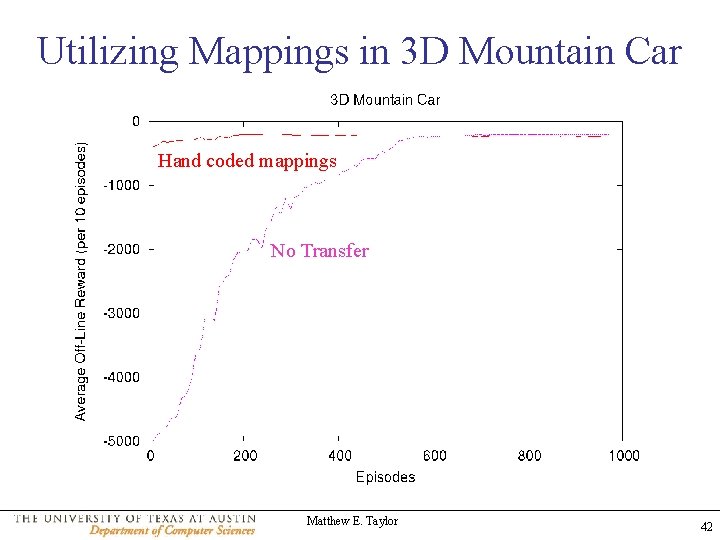
Utilizing Mappings in 3 D Mountain Car Hand coded mappings No Transfer Matthew E. Taylor 42

Experimental Setup • Learn in 2 D Mountain Car for 100 episodes • Learn in 3 D Mountain Car for 25 episodes • Apply MASTER – Train transition model off-line using backprop in Weka • Transfer from 2 D to 3 D: Q-Value Reuse • Learn the 3 D Task Matthew E. Taylor 43

State Variable Mappings x y MSE Evaluated x x 0. 0348 x x x x 0. 0228 x 0. 0090 x x x 0. 0406 0. 0350 x x 0. 0289 0. 0225 x … 0. 0227 x … x 0. 0406 … Matthew E. Taylor 44

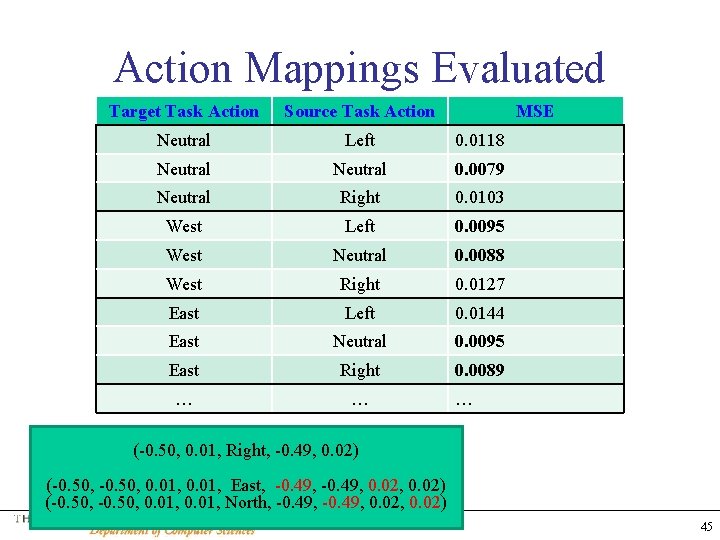
Action Mappings Evaluated Target Task Action Source Task Action MSE Neutral Left 0. 0118 Neutral 0. 0079 Neutral Right 0. 0103 West Left 0. 0095 West Neutral 0. 0088 West Right 0. 0127 East Left 0. 0144 East Neutral 0. 0095 East Right 0. 0089 … … … (-0. 50, 0. 01, Right, -0. 49, 0. 02) (-0. 50, 0. 01, East, -0. 49, 0. 02) (-0. 50, 0. 01, North, -0. 49, 0. 02) Matthew E. Taylor 45

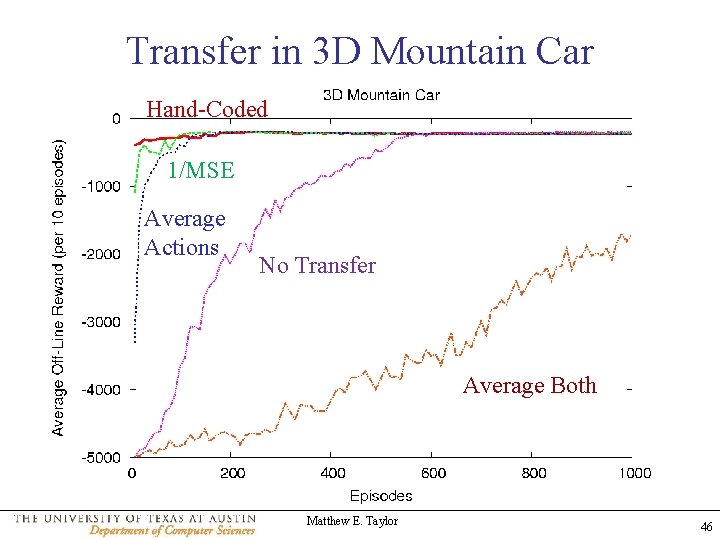
Transfer in 3 D Mountain Car Hand-Coded 1/MSE Average Actions No Transfer Average Both Matthew E. Taylor 46

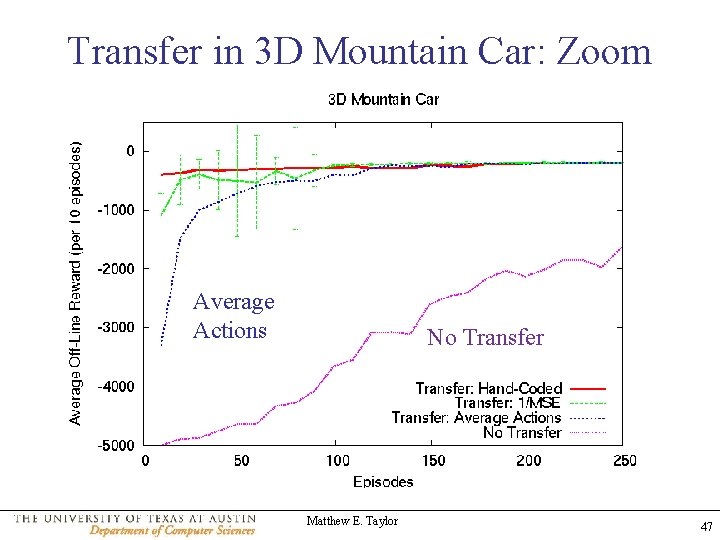
Transfer in 3 D Mountain Car: Zoom Average Actions No Transfer Matthew E. Taylor 47

MASTER Wrap-up • First fully autonomous mapping-learning method • Learning done off-line • Use to select most relevant source task or transfer from multiple source tasks • Future work – Incorporate heuristic search – Use in more complex domains – Formulate as optimization problem? Matthew E. Taylor 48

Outline • • • Reinforcement Learning Background Inter-Task Mappings Value Function Transfer MASTER: Learning Inter-Task Mappings Related Work Future Work and Conclusion Matthew E. Taylor 49

Related Work: Framework • • • Allowed task differences Source task selection Type of knowledge transferred Allowed base learners + 3 others Matthew E. Taylor 50

Selected Related Work: Transfer Methods 1. 2. 3. 4. Same state variables and actions [Selfridge+, 1985] Multi-task learning [Fernandez and Veloso, 2006] Methods to avoid inter-task mappings [Konidaris and Barto, 2007] Different state variables and actions [Torrey+, • ] T(s, a)=s’ Action State Reward s = ⟨x 1, … xn⟩ Matthew E. Taylor 51

Selected Related Work: Mapping Learning Methods On-line: • Test possible mappings on-line as new actions [Soni and Singh, 2006] • k-Armed bandit, each arm is a mapping [Talvite and Singh, 2007] Off-line • Full Qualitative Dynamic Bayes Networks (QDBNs) [Liu and Stone, 2006] Assume T types of task-independent objects Keepaway domain has 2 object types: Keepers and Takers Matthew E. Taylor Hold: 2 vs. 1 Keepaway 52

Outline • • • Reinforcement Learning Background Inter-Task Mappings Value Function Transfer MASTER: Learning Inter-Task Mappings Related Work Future Work and Conclusion Matthew E. Taylor 53

Open Question 1: Optimize for Metrics • Minimize target time: more source task training? 3 vs. 2 to 4 vs. 3 35 • Minimize total time: “moderate” amount of training? • Depends on task similarity Simulator Hours 30 25 20 15 10 5 0 0 10 50 100 250 500 100030006000 3 vs. 2 Avg. Episodes Avg. 3 vs. 2 #time 4 vs. 3 time Matthew E. Taylor 54

Open Question 2: Effects of Task Similarity Source unrelated to Target Source identical to Target Transfer trivial Transfer impossible – Is transfer beneficial for a given pair of tasks? • Avoid Negative Transfer? Matthew E. Taylor 55

Open Question 3: Avoiding Negative Transfer • Currently depends on heuristics and human knowledge • Very similar tasks may not transfer • Need more theoretical analysis – Approximate bisimulation metrics? [Ferns et al. , • ] – Utilize homomorphisms? [Soni and Singh, 2006] Matthew E. Taylor 56

Acknowledgements • Advisor: Peter Stone • Committee: Risto Miikkulainen, Ray Mooney, Bruce Porter, and Rich Sutton • Other co-authors for material in the dissertation: Nick Jong, Greg Kuhlmann, Shimon Whiteson, and Yaxin Liu • LARG Matthew E. Taylor 57

Conclusion • Inter-task mappings can be: – Used with many different RL algorithms – Used in many domains – Learned from interacting with an environment • Plausibility and efficacy have been demonstrated • Next up: Broaden applicability and autonomy Matthew E. Taylor 58

Thanks for your attention! Questions? Matthew E. Taylor 59