Automating Scanner Construction RE NFA Thompsons construction Build

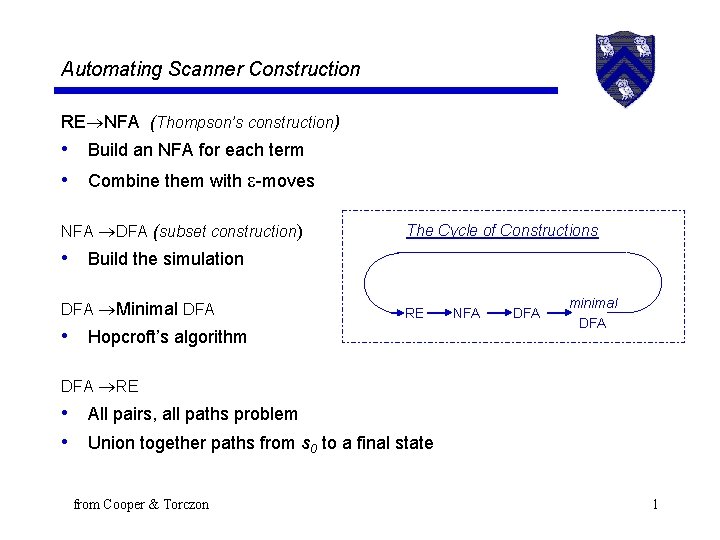
Automating Scanner Construction RE NFA (Thompson’s construction) • Build an NFA for each term • Combine them with -moves NFA DFA (subset construction) The Cycle of Constructions • Build the simulation DFA Minimal DFA RE • Hopcroft’s algorithm NFA DFA minimal DFA RE • All pairs, all paths problem • Union together paths from s 0 to a final state from Cooper & Torczon 1

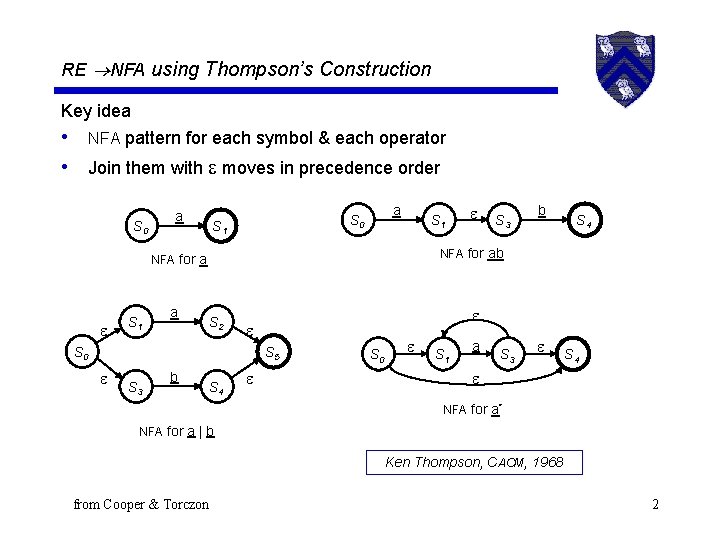
RE NFA using Thompson’s Construction Key idea • NFA pattern for each symbol & each operator • Join them with moves in precedence order S 0 a a S 0 S 1 a S 2 S 5 S 3 b b S 4 S 0 S 3 NFA for ab NFA for a S 1 S 4 S 0 S 1 a S 3 S 4 NFA for a* NFA for a | b Ken Thompson, CACM, 1968 from Cooper & Torczon 2

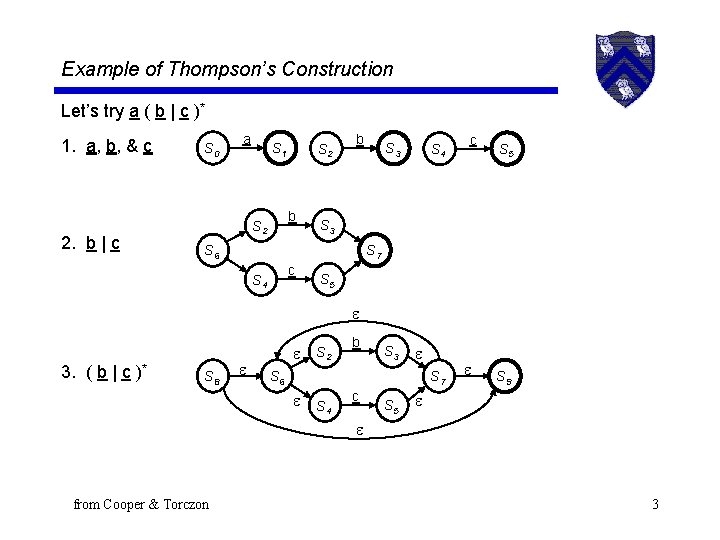
Example of Thompson’s Construction Let’s try a ( b | c )* 1. a, b, & c 2. b | c S 0 a S 1 S 2 b S 3 S 4 c S 5 S 3 S 6 S 7 c S 4 S 5 3. ( b | c )* S 8 S 2 b S 3 S 6 S 7 S 4 c S 5 S 9 from Cooper & Torczon 3

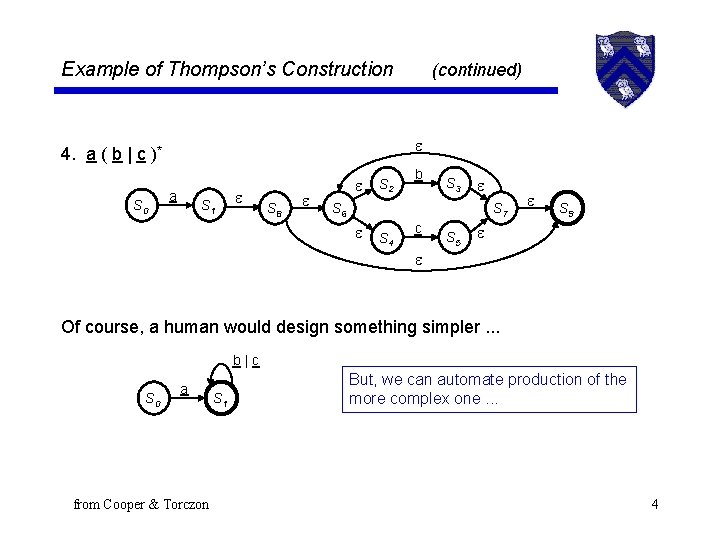
Example of Thompson’s Construction 4. a ( b | c )* S 0 (continued) a S 1 S 8 S 2 b S 3 S 6 S 7 S 4 c S 5 S 9 Of course, a human would design something simpler. . . b|c S 0 a from Cooper & Torczon S 1 But, we can automate production of the more complex one. . . 4

NFA DFA with Subset Construction Need to build a simulation of the NFA Two key functions • Move(si, a) is set of states reachable by a from si • -closure(si) is set of states reachable by from si The algorithm • • Start state derived from s 0 of the NFA Take its -closure Work outward, trying each and taking its -closure Iterative algorithm that halts when the states wrap back on themselves Sounds more complex than it is… from Cooper & Torczon 5

NFA DFA with Subset Construction The algorithm: The algorithm halts: s 0 -closure(q 0 n ) 1. S contains no duplicates (test before adding) while ( S is still changing ) for each si S for each s? -closure(move(si, )) if ( s? S ) then add s? to S as sj T[si, ] sj 2. 2 Qn is finite Let’s think about why this works S and T form the DFA from Cooper & Torczon 3. while loop adds to S, but does not remove from S (monotone) the loop halts S contains all the reachable NFA states It tries each character in each si. It builds every possible NFA configuration. 6

NFA DFA with Subset Construction Example of a fixed-point computation • • Monotone construction of some finite set Halts when it stops adding to the set Proofs of halting & correctness are similar These computations arise in many contexts Other fixed-point computations • Canonical construction of sets of LR(1) items > Quite similar to the subset construction • Classic data-flow analysis (& Gaussian Elimination) > Solving sets of simultaneous set equations We will see many more fixed-point computations from Cooper & Torczon 7

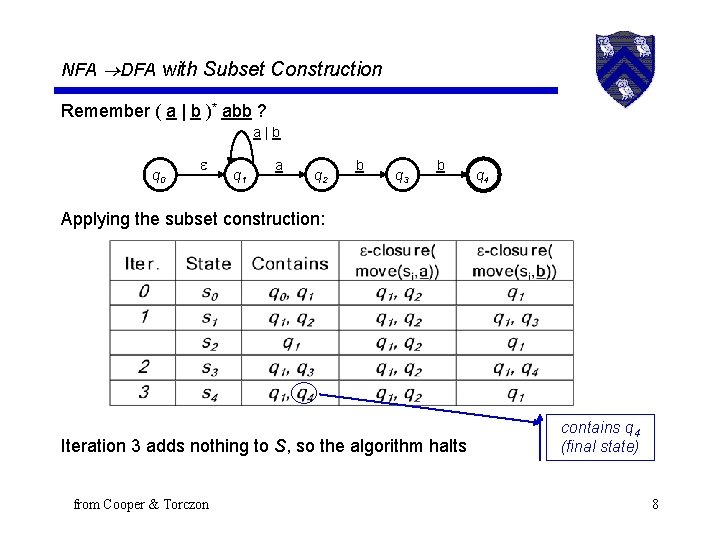
NFA DFA with Subset Construction Remember ( a | b )* abb ? a|b q 0 q 1 a q 2 b q 3 b q 4 Applying the subset construction: Iteration 3 adds nothing to S, so the algorithm halts from Cooper & Torczon contains q 4 (final state) 8

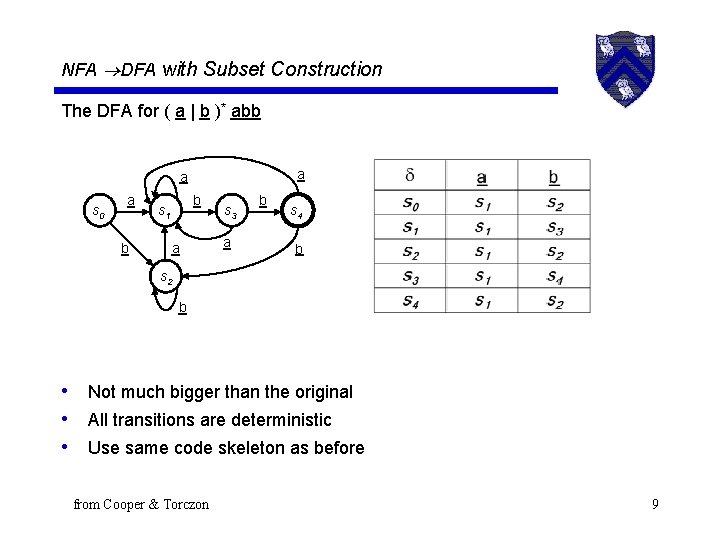
NFA DFA with Subset Construction The DFA for ( a | b )* abb a a s 0 a b b s 1 a s 3 a b s 4 b s 2 b • Not much bigger than the original • All transitions are deterministic • Use same code skeleton as before from Cooper & Torczon 9

Where are we? Why are we doing this? RE NFA (Thompson’s construction) • Build an NFA for each term • Combine them with -moves NFA DFA (subset construction) • Build the simulation The Cycle of Constructions DFA Minimal DFA • Hopcroft’s algorithm RE NFA DFA minimal DFA RE • All pairs, all paths problem • Union together paths from s 0 to a final state Enough theory for today from Cooper & Torczon 10

Building Faster Scanners from the DFA Table-driven recognizers waste a lot of effort • • • Read (& classify) the next character Find the next state Assign to the state variable Trip through case logic in action() Branch back to the top We can do better • • Encode state & actions in the code Do transition tests locally char next character; state s 0 ; call action(state, char); while (char eof) state (state, char); call action(state, char); char next character; if (state) = final then report acceptance; else report failure; Generate ugly, spaghetti-like code Takes (many) fewer operations per input character from Cooper & Torczon 11

Building Faster Scanners from the DFA A direct-coded recognizer for r Digit* goto s 0; s 0: word Ø; char next character; if (char = ‘r’) then goto s 1; else goto se; s 1: word + char; char next character; if (‘ 0’ ≤ char ≤ ‘ 9’) then goto s 2; else goto se; s 2: word + char; char next character; if (‘ 0’ ≤ char ≤ ‘ 9’) then goto s 2; else if (char = eof) then report acceptance; else goto se; se: print error message; return failure; • Many fewer operations per character • Almost no memory operations • Even faster with careful use of fall-through cases from Cooper & Torczon 12

Building Faster Scanners Hashing keywords versus encoding them directly • Some compilers recognize keywords as identifiers and check them in a hash table (some well-known compilers do this!) • Encoding it in the DFA is a better idea > O(1) cost per transition > Avoids hash lookup on each identifier It is hard to beat a well-implemented DFA scanner from Cooper & Torczon 13