Automating Abstract Interpretation and Creating Improved Decision Procedures
Automating Abstract Interpretation and Creating Improved Decision Procedures as a Bonus Thomas Reps University of Wisconsin and Gramma. Tech, Inc.
Unexpected Linkages Computer Architecture Operating Systems Networking Software Engineering Programming Languages Machine Learning Automated Reasoning 2
• The administrator of the U. S. S. Yorktown’s Standard Monitoring Control System entered 0 into a data field for the Remote Data Base Manager program. That caused the database to overflow and crash all LAN consoles and miniature remote terminal units • The Yorktown was dead in the water for about two hours and 45 minutes 3
Analysis must track numeric information • A sailor on the U. S. S. Yorktown entered a 0 into a data field in a kitchen-inventory program • That caused an overflow, which crashed all LAN consoles and miniature remote terminal units • The Yorktown was dead in the water for about two hours and 45 minutes 4
x = 3; y = 1/(x-3); need to track values other than 0 x = 3; px = &x; y = 1/(*px-3); need to track heap-allocated storage need to track pointers x = 3; p = (int*)malloc(sizeof int); *p = x; q = p; y = 1/(*q-3);
Static Analysis in a Nutshell • Determine information about the possible situations that can arise at execution time, without actually running the program on specific inputs • Typically: – For each point in the program, find a descriptor that represents (a superset of) the stores that could possibly arise at that point • Correctness of an analysis justified via abstract interpretation [Cousot & Cousot 77] 6
Automating Abstraction Interpretation • Abstract interpretation – A “black art” hard to work with • 20 -year quest to raise the level of automation in abstract interpretation – 3 -valued logic analysis (TVLA) • with M. Sagiv, R. Wilhelm, T. Lev-Ami, A. Loginov, & many others – machine-code analysis (TSL) • with J. Lim – symbolic-abstraction algorithms • with M. Sagiv, G. Yorsh, A. Thakur Reps, T. and Thakur, A. , “Automating abstract interpretation, ” VMCAI, 2016. research. cs. wisc. edu/wpis/papers/vmcai 16 -invited. pdf Patrick Cousot Radhia Cousot
What Does It Mean to Automate Parsing? • A parsing-problem instance Parse(L, s) has two inputs – L = a context-free language – s = a string to be parsed The string changes more frequently than the language • A context-free language has a context-free grammar • Yacc (and later, Gnu Bison) – Input: a context-free grammar that describes the language L to be parsed – Output: a parsing function, yyparse(), for which executing yyparse() on string s computes Parse(L, s) Steve Johnson 8 source: simple-talk interview
What Does It Mean to Automate Program Analysis? • Follow a similar scheme. . . • But first, why would you even want to invest the time doing so? 9
10
11
12
Why is Program Analysis Difficult? • 13
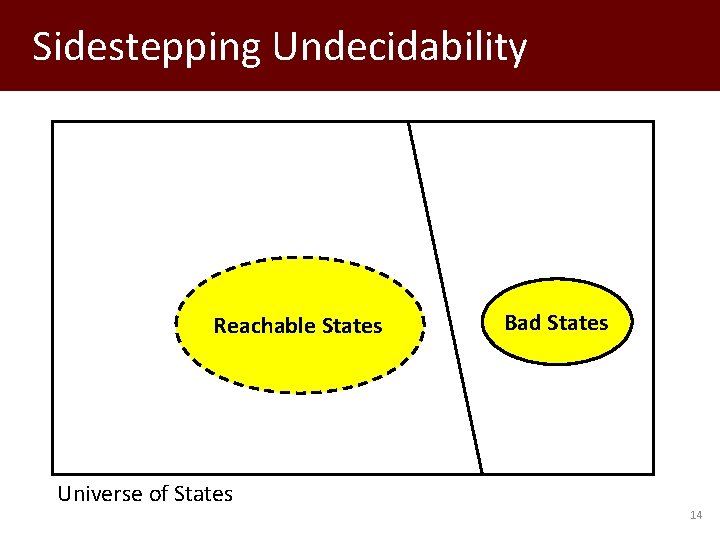
Sidestepping Undecidability Reachable States Bad States Universe of States 14
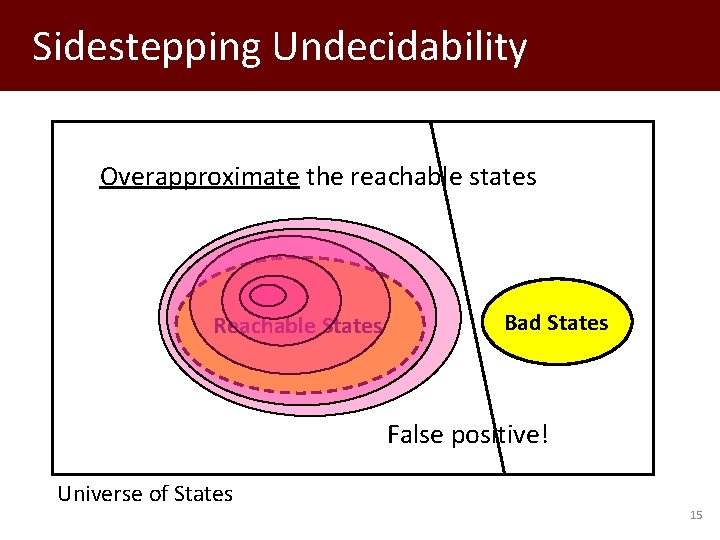
Sidestepping Undecidability Overapproximate the reachable states Reachable States Bad States False positive! Universe of States 15
Why is Program Analysis Difficult? • 16
Why is Program Analysis Difficult? • Large/unbounded base types: int, float, string • User-defined types/classes • Pointers/aliasing + unbounded #’s of heap-allocated cells • Procedure calls/recursion/calls through pointers/dynamic method lookup/overloading • Concurrency + unbounded #’s of threads 17
Sources of Infinity • Data – unbounded counters, integer variables, lists, queues • Control structures – procedures, process creation • Configuration parameters – unbounded number of processes, principals • Real-time – discrete or continuous time 18
Some Successes of the Field • Static Driver Verifier, a. k. a. SLAM (Microsoft) – Tool for finding possible bugs in Windows device drivers – Complicated back-out protocols in driver APIs when events cancelled or interrupted • Astrée (ENS) – Established the absence of run-time errors in Airbus flight software 19
Outline • • • Gentle introduction to abstract interpretation First glimmer of insight Second insight Third insight Di. SSolve: A parallel SAT solver Wrap-up 20
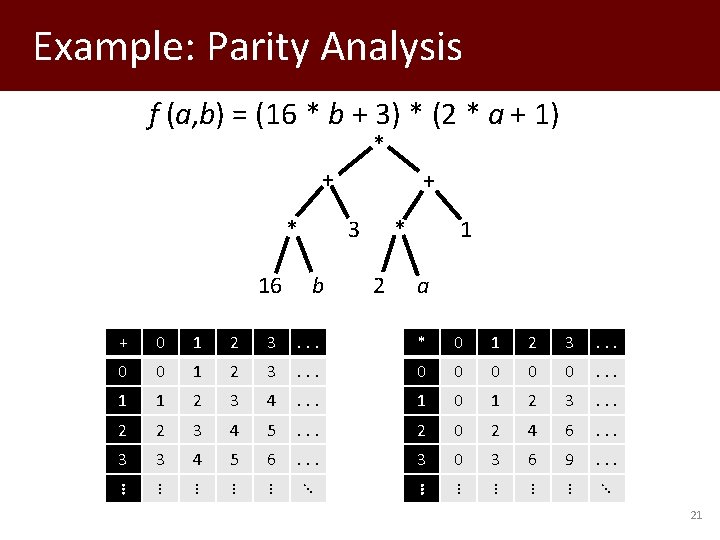
Example: Parity Analysis f (a, b) = (16 * b + 3) * (2 * a + 1) * + * 16 + * 3 b 2 1 a + 0 1 2 3 . . . * 0 1 2 3 . . . 0 0 0 . . . 1 1 2 3 4 . . . 1 0 1 2 3 . . . 2 2 3 4 5 . . . 2 0 2 4 6 . . . 3 3 4 5 6 . . . 3 0 3 6 9 . . . ⋮ ⋮ ⋮ ⋮ ⋮ ⋱ 21
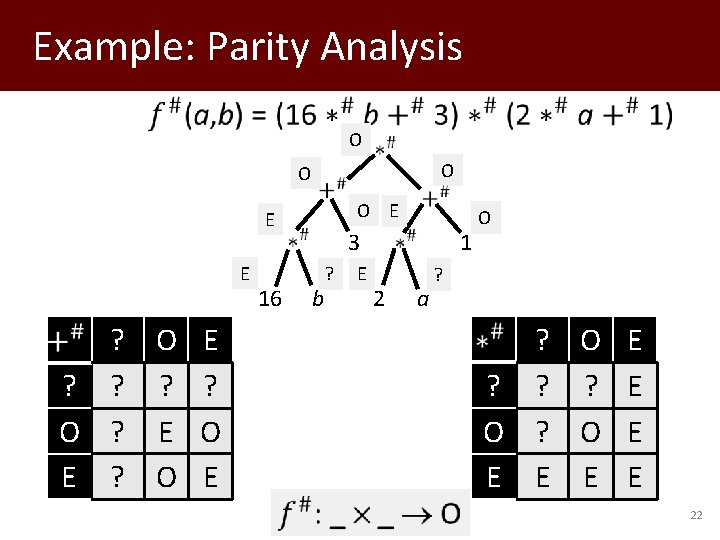
Example: Parity Analysis O O O E E E ? O E ? ? O ? E O E ? O E 16 3 b ? E O 2 1 a O ? ? O E ? ? ? E O ? O E E E 22
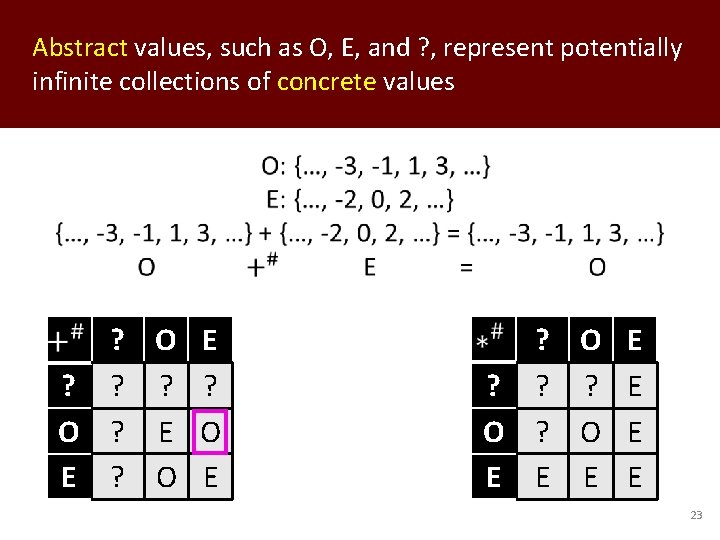
Abstract values, such as O, E, and ? , represent potentially infinite collections of concrete values ? O E ? ? O ? E O E ? ? ? E O ? O E E E 23
![Constant Propagation [i ? , j ? ] i = 0 e. e[i 0]](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-24.jpg "Constant Propagation [i ? , j ? ] i = 0 e. e[i 0]")
Constant Propagation [i ? , j ? ] i = 0 e. e[i 0] [i 0, j ? ] j = 0 e. e[j 0] e. e [i 0, j 0] [i 1, j 0] while i 2 e. e [i 0, j 0] j = (j+1)/4 e. e[j (e(j)+1)/4] [i 0, j 0] i = i+1 printf(i, j) e. e[i e(i) + 1] [i 0, j 0] 24
![Constant Propagation [i ? , j ? ] i = 0 e. e[i 0]](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-25.jpg "Constant Propagation [i ? , j ? ] i = 0 e. e[i 0]")
Constant Propagation [i ? , j ? ] i = 0 e. e[i 0] [i 0, j ? ] j = 0 e. e[j 0] e. e [i ? , j 0] while (…) e. e [i [i 0, ? , j 0] j = (j+1)/4 e. e[j (e(j)+1)/4] i {…, -2, -1, 0, 1, 2, …} [i 0, ? , j 0] j {0} i = i+1 printf(i, j) e. e[i e(i) + 1] [i 0, ? , j 0] 25
What Does It Mean to Automate Abstract Interpretation? • 26
![Abstract Interpretation [CC 77] {(x 2, y 1), (x 5, y 3)} {(2, 1),](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-27.jpg "Abstract Interpretation [CC 77] {(x 2, y 1), (x 5, y 3)} {(2, 1),")
Abstract Interpretation [CC 77] {(x 2, y 1), (x 5, y 3)} {(2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3)} γ x [2, 5] y [1, 3] α α Universe of States Patrick Cousot Radhia Cousot
![Best Transformer [CC 79] However, no algorithms to • apply the best transformer •](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-28.jpg "Best Transformer [CC 79] However, no algorithms to • apply the best transformer •")
Best Transformer [CC 79] However, no algorithms to • apply the best transformer • create the best transformer Loss of precision τ ττ τ τ ττ γ α γ safe τ# τ# Universe of States Patrick Cousot Radhia Cousot
![Challenge: Abstract Interpretation is [-5, 5] Inherently Non-Compositional [5, 10] [-10, -5] x •](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-29.jpg "Challenge: Abstract Interpretation is [-5, 5] Inherently Non-Compositional [5, 10] [-10, -5] x •")
Challenge: Abstract Interpretation is [-5, 5] Inherently Non-Compositional [5, 10] [-10, -5] x • In computer science, we rely on compositionality – – languages are expressed using context-free grammars [5, 10] x many concepts and properties defined using inductive definitions recursive tree traversals are a basic workhorse software organized into layers • Example: (x + (–x)), evaluated in (x ↦ [5, 10], y ↦ [10, 20]) – [-5, 5] versus [0, 0] • In general – Suppose that you have in hand a collection of ``best” abstractinterpretation operators – Their composition may not provide the best (abstract) answer for the composition of the corresponding concrete operations 29
Automating Abstraction Interpretation Q 1. What formalism is used to specify Ms? • Abstract interpretation Q 2. What formalism is used to specify A? Q 3. What is the engine at work that applies/constructs – A “black art” hard to work with abstract transformers? • 20 -year quest to raise the level of automation in (a) What method is used to create Is, A(·)? abstract interpretation (b) Can it be used to create a representation of Is, A(·)? – 3 -valued logic analysis (TVLA) Q 4. How is the non-compositionality issue addressed? • with M. Sagiv, R. Wilhelm, T. Lev-Ami, A. Loginov, & many others – machine-code analysis (TSL) • with J. Lim – symbolic-abstraction algorithms • with M. Sagiv, G. Yorsh, A. Thakur Reps, T. and Thakur, A. , “Automating abstract interpretation, ” VMCAI, 2016. research. cs. wisc. edu/wpis/papers/vmcai 16 -invited. pdf Patrick Cousot Radhia Cousot
Outline • • • Gentle introduction to abstract interpretation First glimmer of insight Second insight Third insight Di. SSolve: A parallel SAT solver Wrap-up 31
A First Glimmer 40% of the people in the Wisconsin CS department are doing machine learning, but don’t know it Jude Shavlik R. , Sagiv, & Yorsh: Symbolic implementation of the best transformer , VMCAI 2004 Mooly Sagiv Greta Yorsh
![Symbolic Abstraction (x ↦ [5, 10]) ⇝ 5 ≤ x ˄ x ≤ 10](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-33.jpg "Symbolic Abstraction (x ↦ [5, 10]) ⇝ 5 ≤ x ˄ x ≤ 10")
Symbolic Abstraction (x ↦ [5, 10]) ⇝ 5 ≤ x ˄ x ≤ 10 Interval ⇝ conjunction of environment single-variable inequalities States L A Typically, L is a rich language and A is an impoverished logic fragment L'. Symbolic abstraction addresses a fundamental approximation problem: Given L, find the strongest consequence of that is expressible in L'. 33
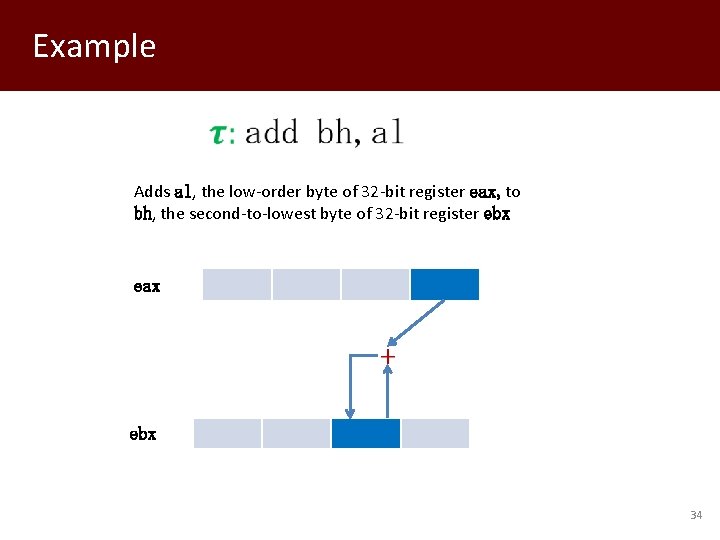
Example Adds al, the low-order byte of 32 -bit register eax, to bh, the second-to-lowest byte of 32 -bit register ebx eax ebx 34
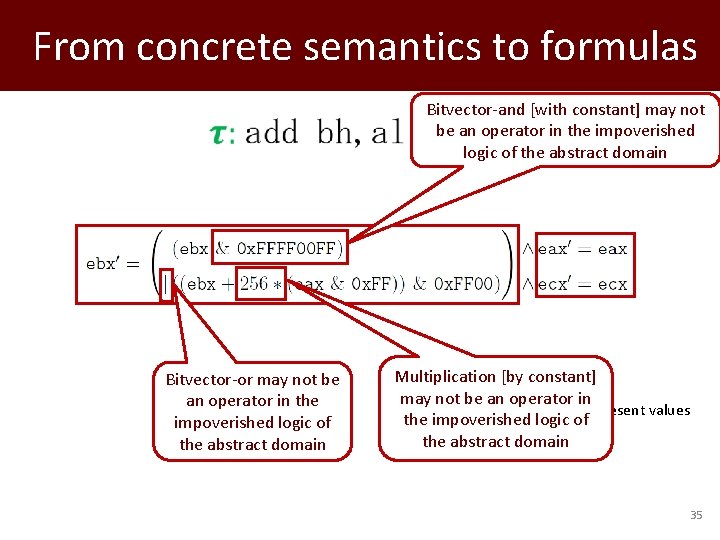
From concrete semantics to formulas Bitvector-or may not be an operator in the impoverished logic of the abstract domain Bitvector-and [with constant] may not be an operator in the impoverished logic of the abstract domain Multiplication [by constant] may not be an operator in Primed variables represent values the impoverished logic of in the post-state the abstract domain 35
Abstract Transformer via Quantifier Elimination? Eliminate unprimed registers
Best Transformer via Symbolic Abstraction
What Does It Mean to Automate Abstract Interpretation? • Use logic, such as quantifier-free bitvector arithmetic (QF_ABV) 38
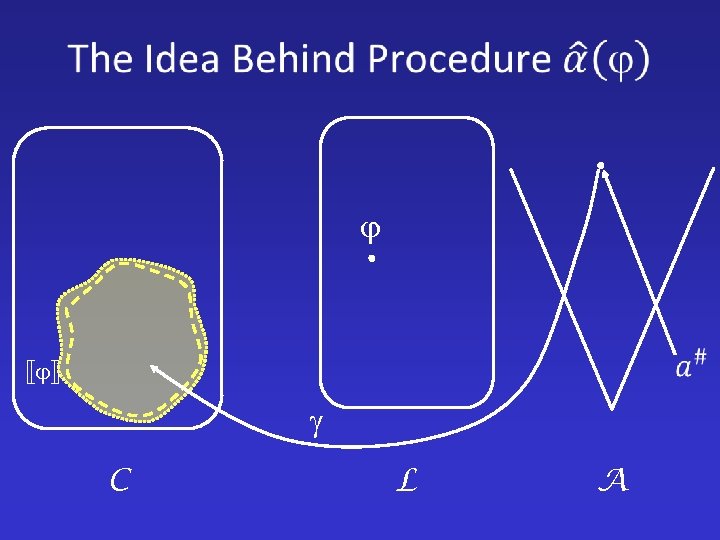
C L A
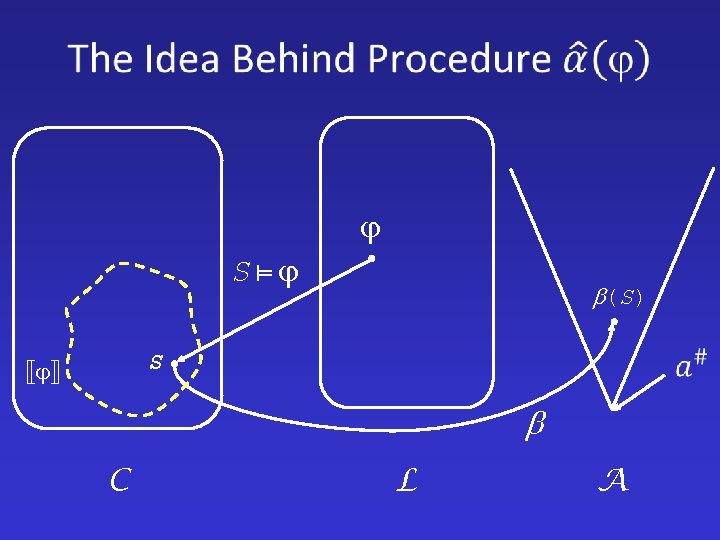
S (S) S C L A
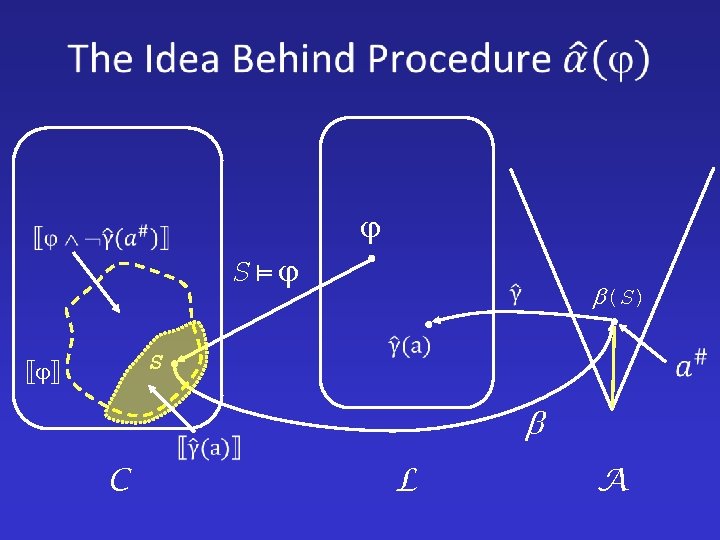
S S C (S) L A
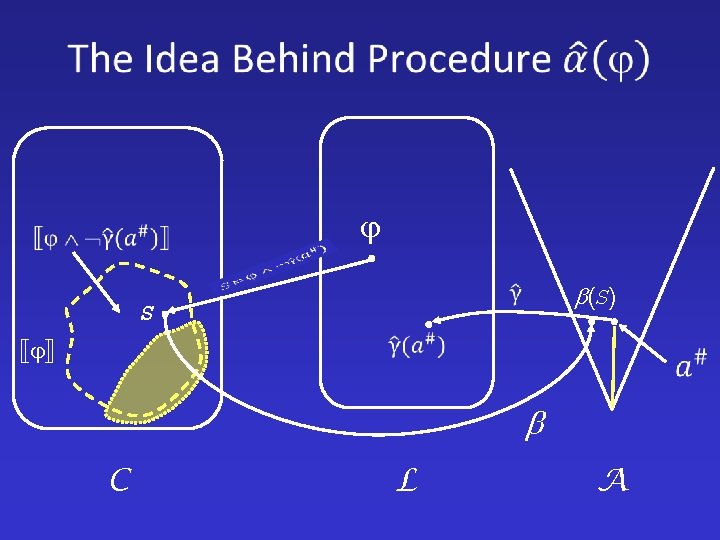
(S) S C L A
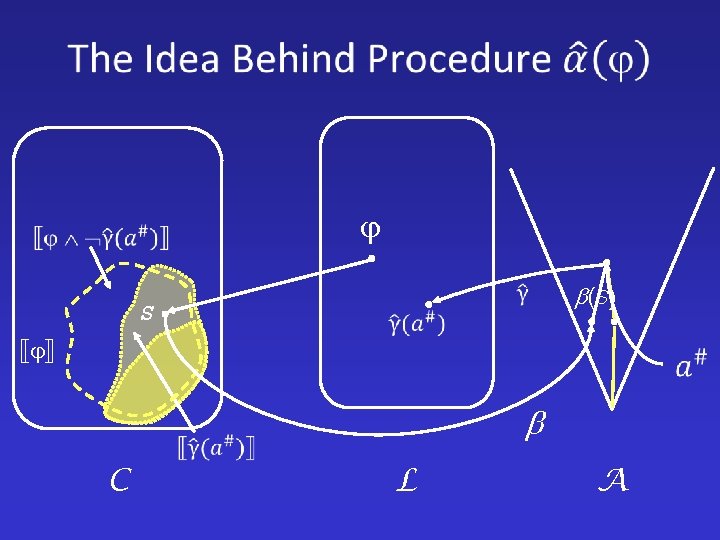
(S) S C L A
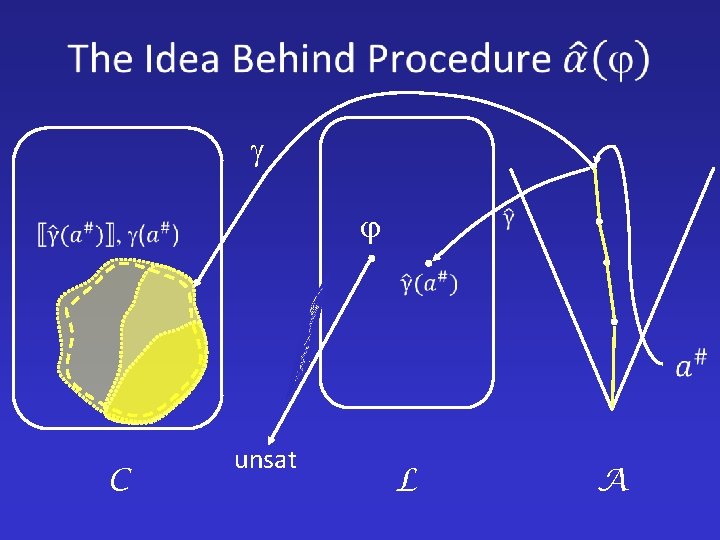
C unsat L A
R. , Sagiv, & Yorsh: Symbolic implementation of the best transformer , VMCAI 2004 Mooly Sagiv Greta Yorsh
![[x 43, y 0] S [x 43, y 0] Concrete Values Formulas Abstract](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-47.jpg "[x 43, y 0] S [x 43, y 0] Concrete Values Formulas Abstract")
[x 43, y 0] S [x 43, y 0] Concrete Values Formulas Abstract Values
![(x = 43) (y = 0) [x 43, y 0] S [x 43,](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-48.jpg "(x = 43) (y = 0) [x 43, y 0] S [x 43,")
(x = 43) (y = 0) [x 43, y 0] S [x 43, y 0] Concrete Values Formulas Abstract Values
![[x 43, y 0] Concrete Values Formulas Abstract Values](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-49.jpg "[x 43, y 0] Concrete Values Formulas Abstract Values")
[x 43, y 0] Concrete Values Formulas Abstract Values
![[x 46, y 0] S [x 46, y 0] Concrete Values Formulas [x](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-51.jpg "[x 46, y 0] S [x 46, y 0] Concrete Values Formulas [x")
[x 46, y 0] S [x 46, y 0] Concrete Values Formulas [x 43, y 0] Abstract Values
![[x T, y 0] S (y = 0) [x 46, y 0] Concrete](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-52.jpg "[x T, y 0] S (y = 0) [x 46, y 0] Concrete")
[x T, y 0] S (y = 0) [x 46, y 0] Concrete Values Formulas Abstract Values
![[x T, y 0] Concrete Values unsat Formulas Abstract Values](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-53.jpg "[x T, y 0] Concrete Values unsat Formulas Abstract Values")
[x T, y 0] Concrete Values unsat Formulas Abstract Values
What Does It Mean to Automate Abstract Interpretation? • 54
A First Glimmer 40% of the people in the Wisconsin CS department are doing machine learning, but don’t know it Jude Shavlik Find-S Algorithm for learning a concept in a concept lattice: • Discard all negative examples • Return the join of all positive examples 55
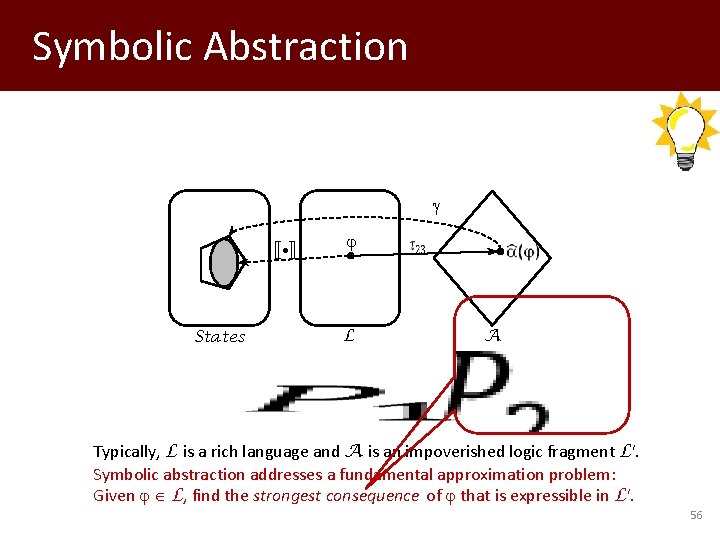
Symbolic Abstraction States L A Typically, L is a rich language and A is an impoverished logic fragment L'. Symbolic abstraction addresses a fundamental approximation problem: Given L, find the strongest consequence of that is expressible in L'. 56
Abstract Transformer via Quantifier Elimination?
The Story in a Nutshell • 58
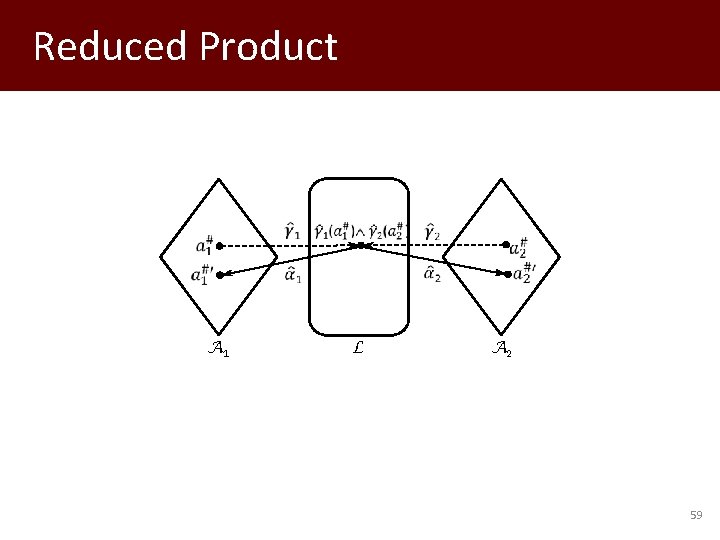
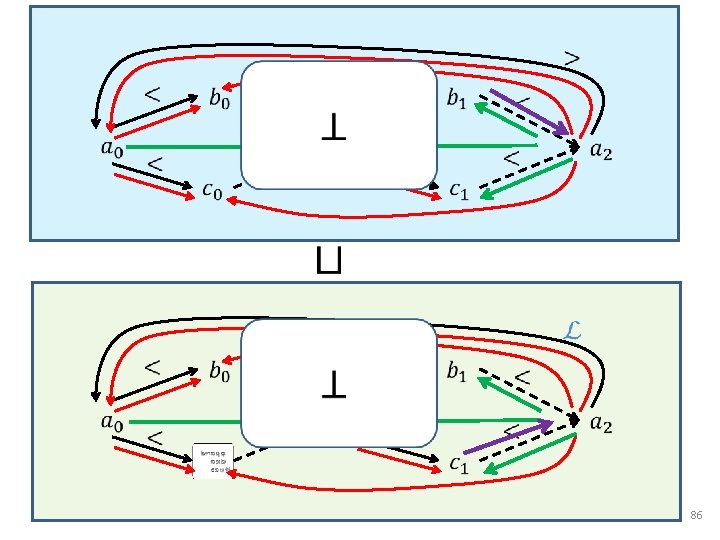
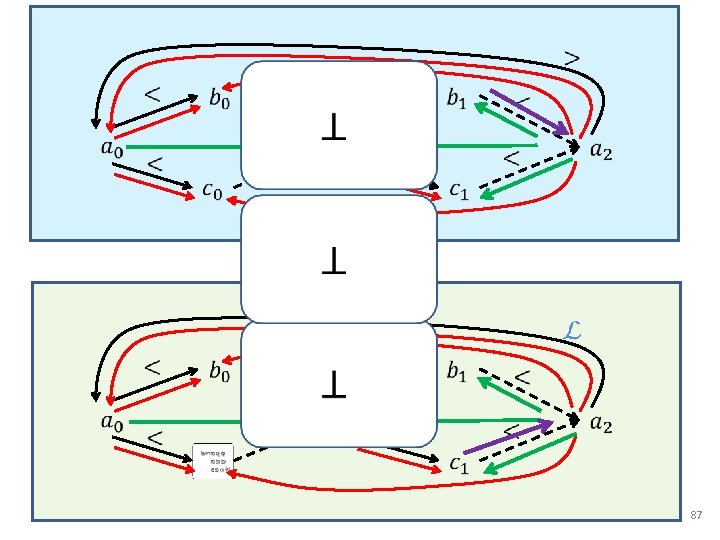
Reduced Product A 1 L A 2 59
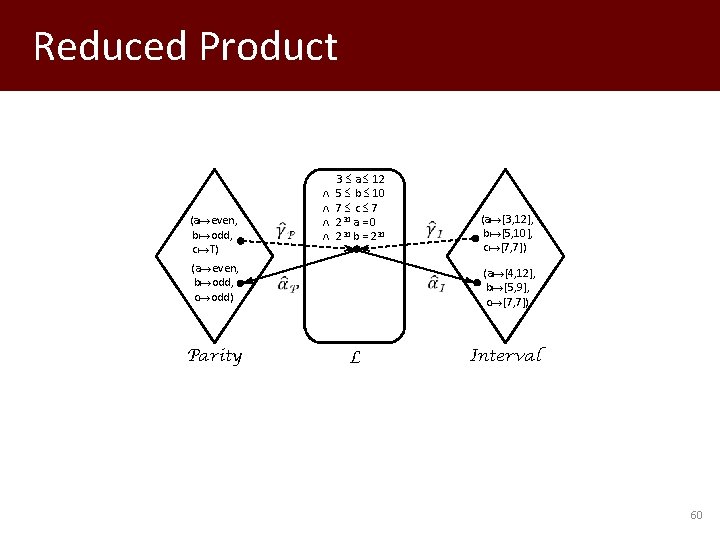
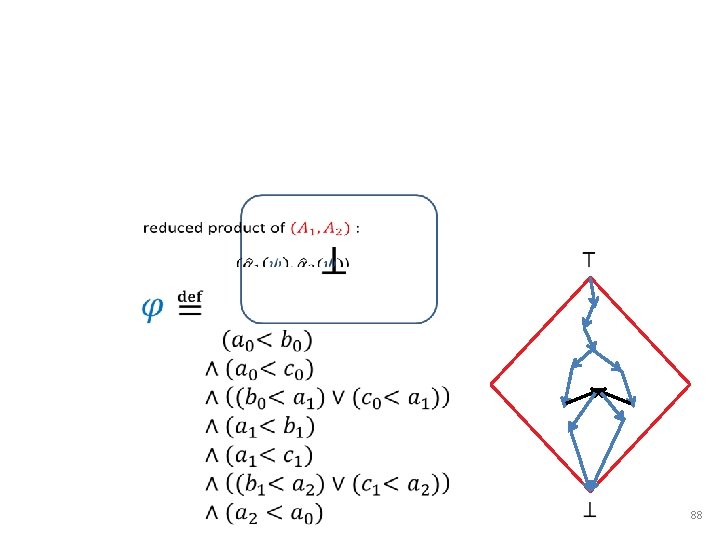
Reduced Product (a even, b odd, c Τ) (a even, b odd, c odd) Parity 3 a 12 5 b 10 7 c 7 231 a = 0 231 b = 231 L (a [3, 12], b [5, 10], c [7, 7]) (a [4, 12], b [5, 9], c [7, 7]) Interval 60
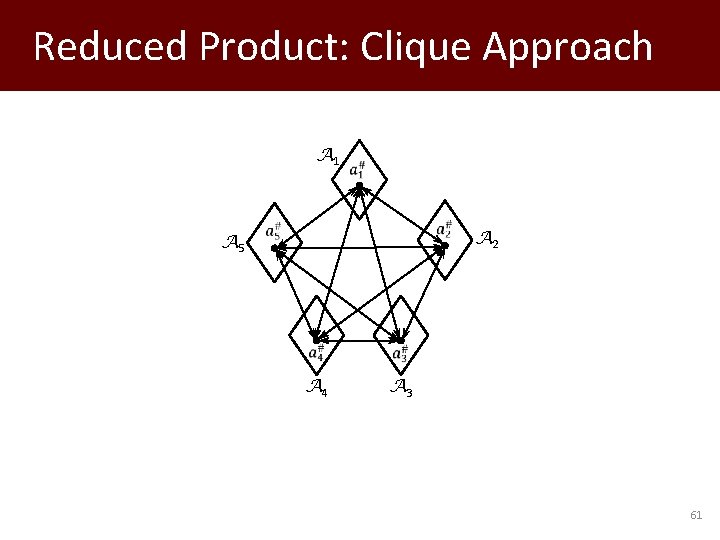
Reduced Product: Clique Approach A 1 A 5 A 4 A 3 A 2 61
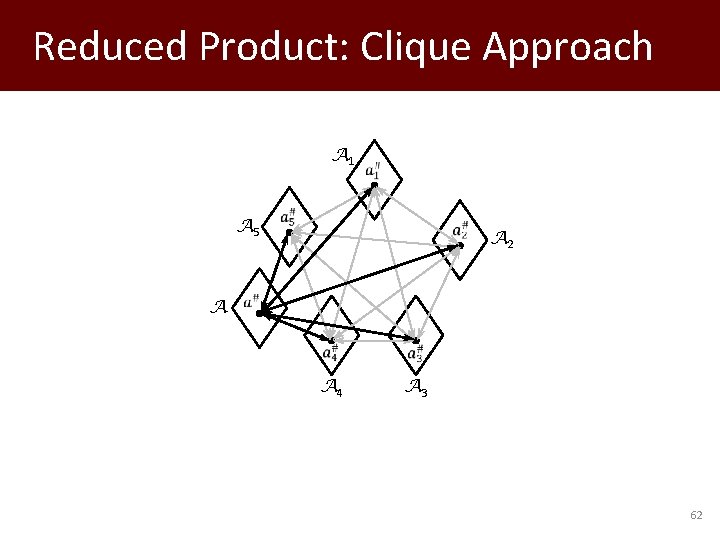
Reduced Product: Clique Approach A 1 A 5 A A 2 A 4 A 3 62
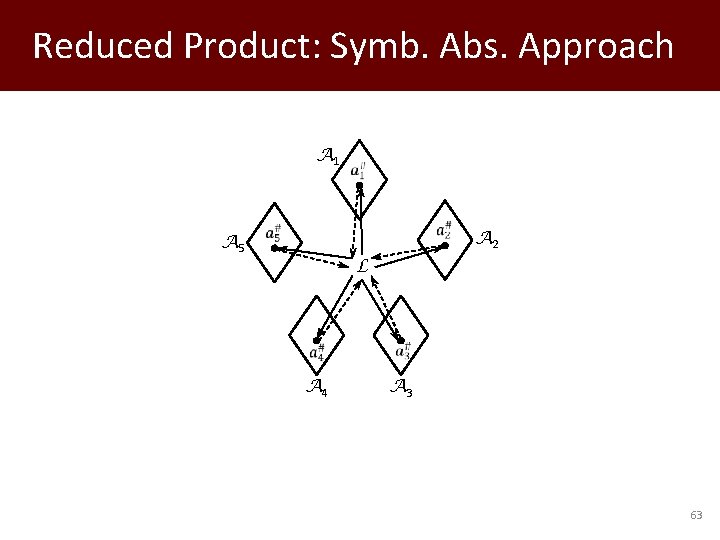
Reduced Product: Symb. Abs. Approach A 1 A 5 A 2 L A 4 A 3 63
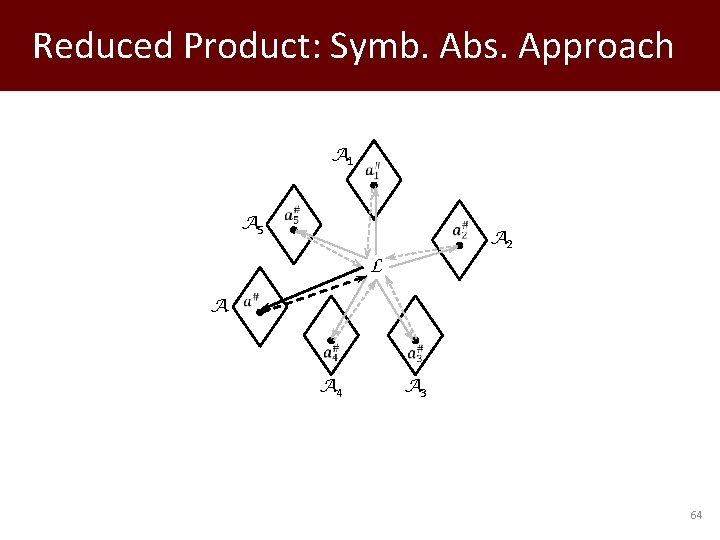
Reduced Product: Symb. Abs. Approach A 1 A 5 A 2 L A A 4 A 3 64
The Story in a Nutshell • 66
The Story in a Nutshell • 67
Outline • 68
Stålmarck’s method Propagation Rules 69
Stålmarck’s method Propagation Rules 70
Stålmarck’s method Propagation Rules 71
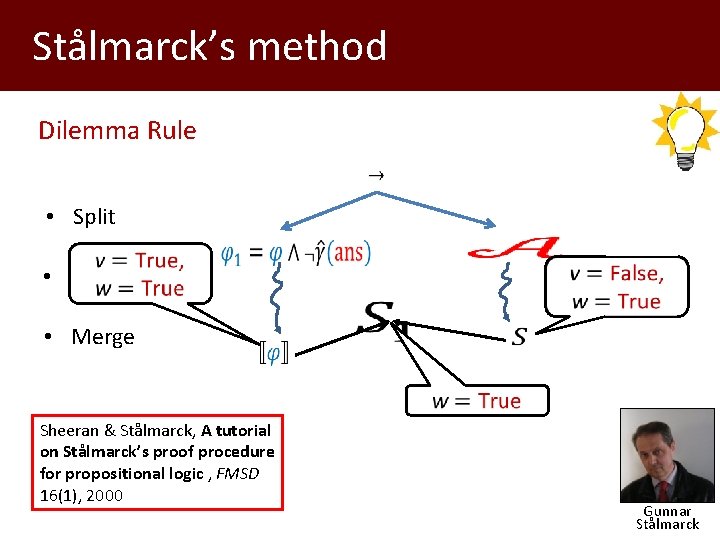
Stålmarck’s method Dilemma Rule • Split • Propagate • Merge Sheeran & Stålmarck, A tutorial on Stålmarck’s proof procedure for propositional logic , FMSD 16(1), 2000 Gunnar Stålmarck
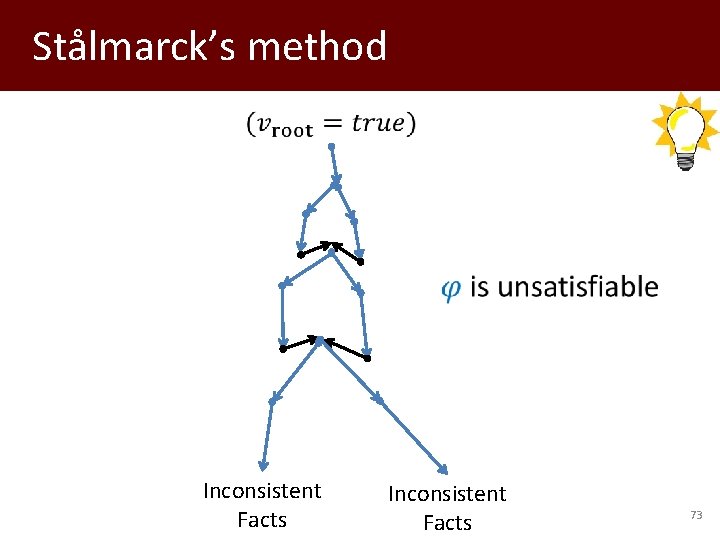
Stålmarck’s method Inconsistent Facts 73
Key Insight Stålmarck 74
Key Insight Abstract Interpretation 75
Key Insight 76
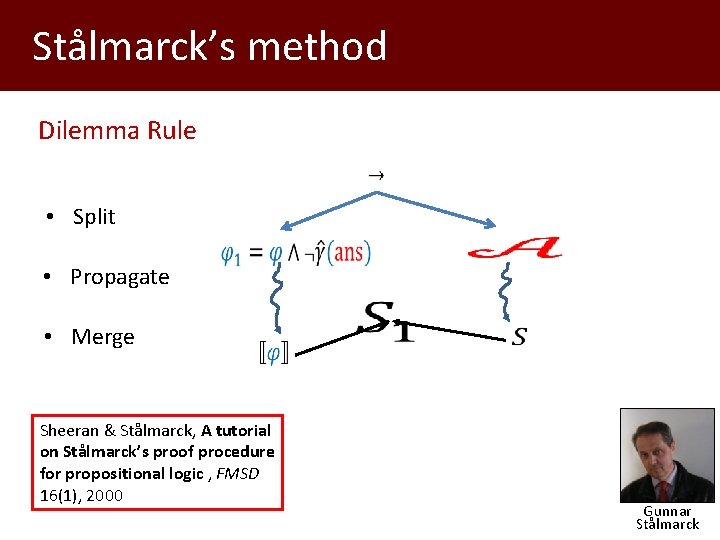
Stålmarck’s method Dilemma Rule • Split • Propagate • Merge Sheeran & Stålmarck, A tutorial on Stålmarck’s proof procedure for propositional logic , FMSD 16(1), 2000 Gunnar Stålmarck
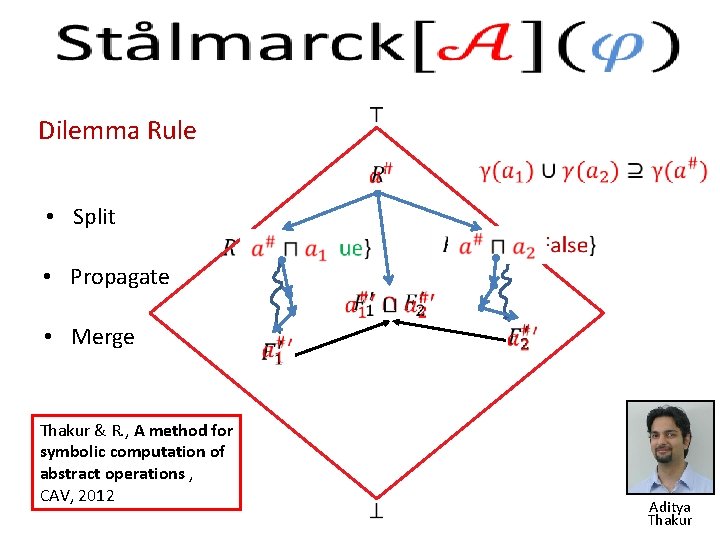
Dilemma Rule • Split • Propagate • Merge Thakur & R. , A method for symbolic computation of abstract operations , CAV, 2012 Aditya Thakur
![Stålmarck = Stålmarck[Equivalence] 79](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-78.jpg "Stålmarck = Stålmarck[Equivalence] 79")
Stålmarck = Stålmarck[Equivalence] 79
Key Insight propositional logic Thakur & R. , A generalization of Stålmarck’s method , SAS, 2012
Key Insight richer logic QF_LRA logic (quantifier-free linear rational arithmetic) QF_ABV logic (quantifier-free bit-vector arithmetic) Thakur & R. , A method for symbolic computation of abstract operations , 81
![Stålmarck[Boolean, Polyhedra] for LRA Dilemma Rule 82](http://slidetodoc.com/presentation_image/2cc38ee8f73400ae68c0039f0be338c9/image-81.jpg "Stålmarck[Boolean, Polyhedra] for LRA Dilemma Rule 82")
Stålmarck[Boolean, Polyhedra] for LRA Dilemma Rule 82
83
84
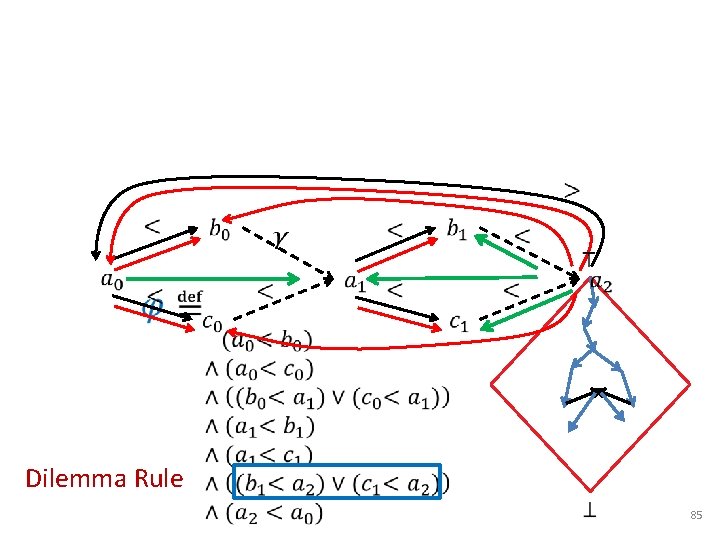
Dilemma Rule 85
86
87
88
… Generalize example to k “diamonds” 89
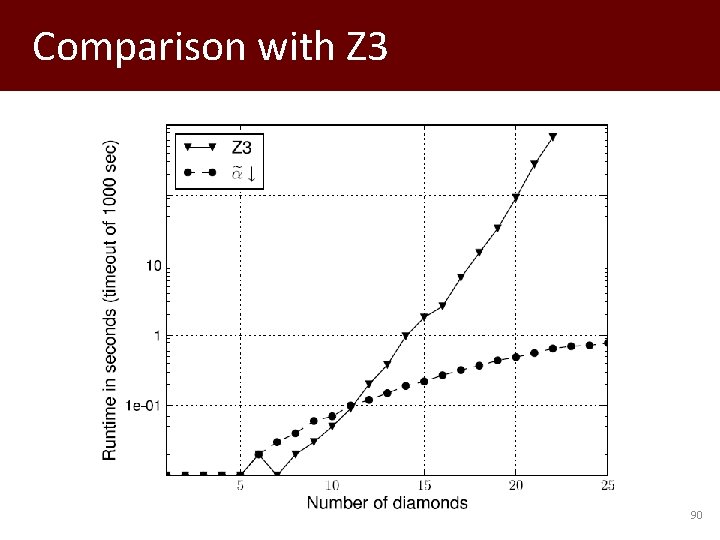
Comparison with Z 3 90
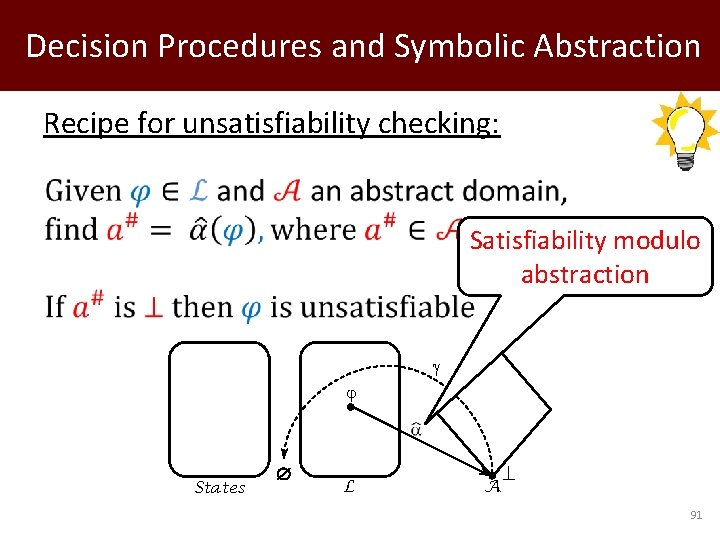
Decision Procedures and Symbolic Abstraction Recipe for unsatisfiability checking: Satisfiability modulo abstraction States L ⊥ A 91
A plea: Decision-procedure developers should generalize their APIs to make available the residuals of “failed” refutations 92
Symbolic Abstraction: Dual-Use 93
94
Outline • • • Gentle introduction to abstract interpretation First glimmer of insight Second insight Third insight Di. SSolve: A parallel SAT solver Wrap-up 95
A Similar Contemporaneous Insight! DPLL/CDCL SAT Solver Vijay D’Silva Leo Haller Daniel Kroening
A Similar Contemporaneous Insight! Abstract Interpretation Vijay D’Silva Leo Haller Daniel Kroening
Outline • • • Gentle introduction to abstract interpretation First glimmer of insight Second insight Third insight Di. SSolve: A parallel SAT solver Wrap-up 98
Di. SSolve: A Parallel SAT solver • Dilemma Rule is trivially parallelizable • Stålmarck’s method not competitive with modern SAT solvers – Use an existing SAT solver – Use rule that is not-quite Dilemma rule 99
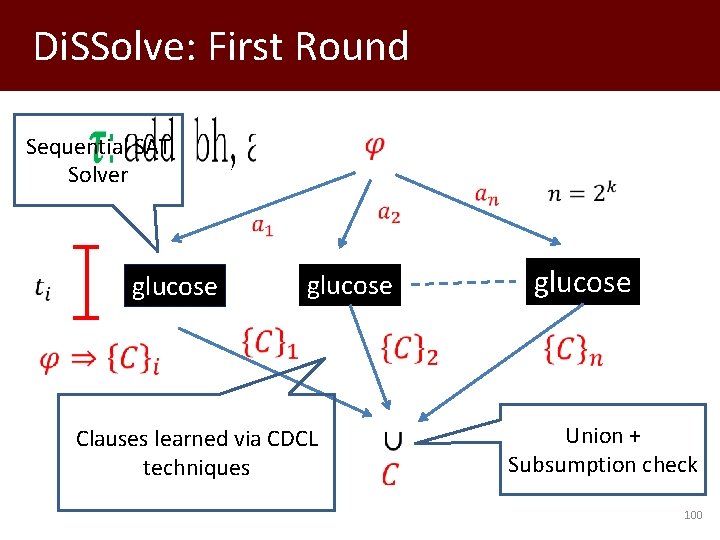
Di. SSolve: First Round Sequential SAT Solver glucose Clauses learned via CDCL techniques glucose Union + Subsumption check 100
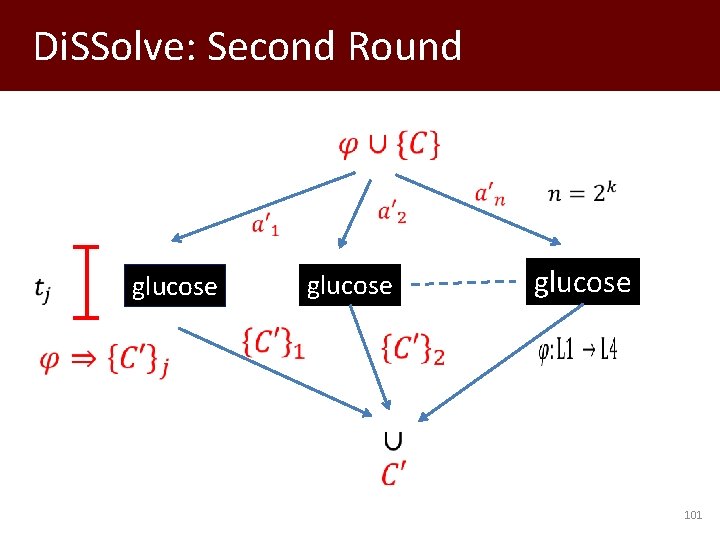
Di. SSolve: Second Round glucose 101
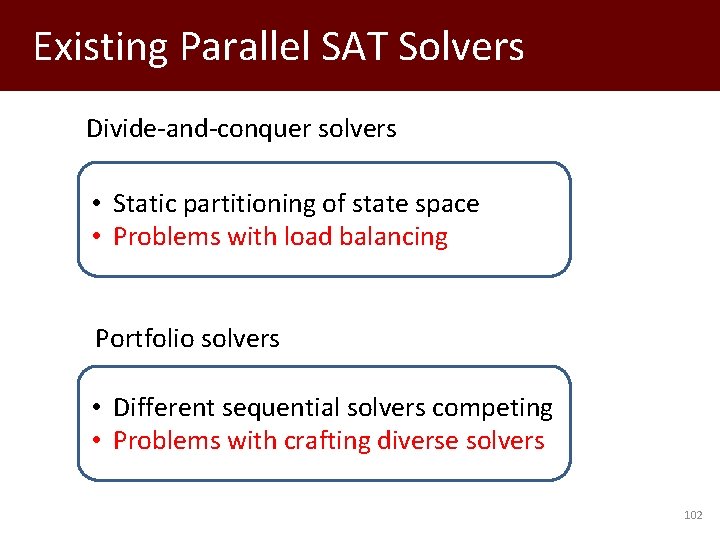
Existing Parallel SAT Solvers Divide-and-conquer solvers • Static partitioning of state space • Problems with load balancing Portfolio solvers • Different sequential solvers competing • Problems with crafting diverse solvers 102
Di. SSolve • Dynamic partitioning of state space • Each solver works on a separate portion of the search space • Frequent communication of learned information • Reuses engineering effort and heuristics from an existing solver (Glucose) – – – Variable ranking Clause ranking Restart schedule Phase saving Final-conflict clauses 103
Di. SSolve on a 32 -Core Machine • Compare sequential and portfolio method with two variants of Di. SSolve – dilemma-style 32 -way case split – 32 -way search using fresh random seeds • Benchmarks from application track of SAT-COMP’ 13 • Timeout of 1000 seconds 104
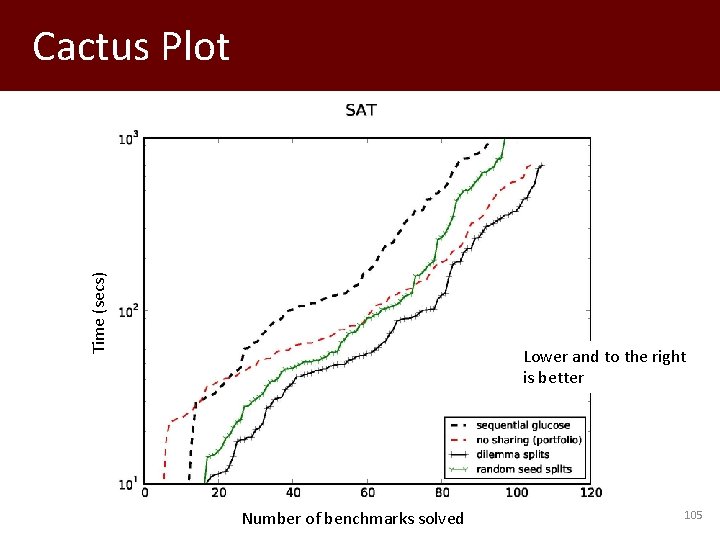
Time (secs) Cactus Plot Lower and to the right is better Number of benchmarks solved 105
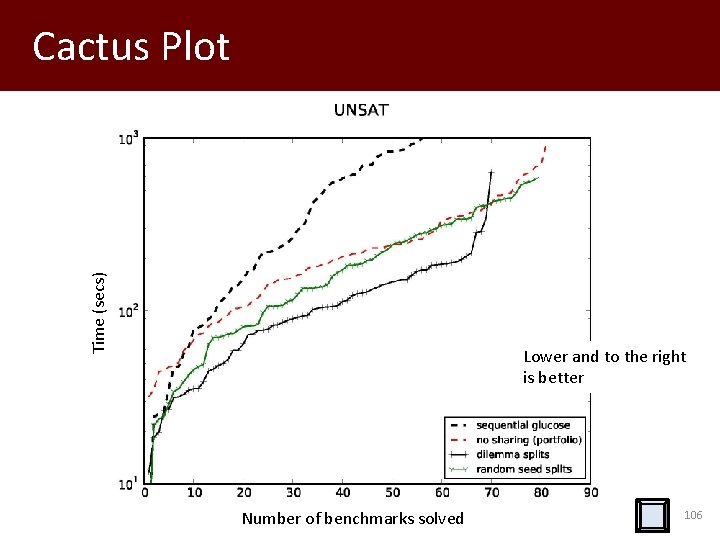
Time (secs) Cactus Plot Lower and to the right is better Number of benchmarks solved 106
Di. SSolve on the Cloud • 107
Di. SSolve on the Cloud Benchmark k_unsat. cnf ctl_4291_567_unsat. cnf gss-25 -s 100. cnf Type Dissolve[128] Di. SSolve[256] UNSAT 1101 655 UNSAT 812 427 SAT 1780 349 • 7 timeouts (Dissolve[128]) 108
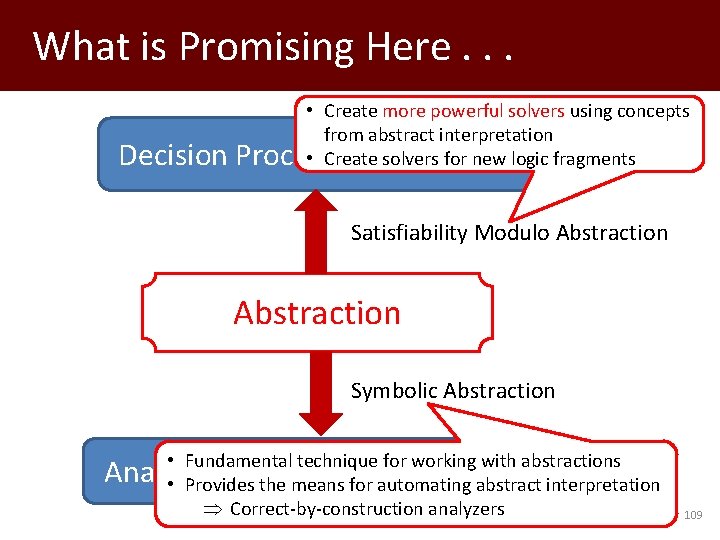
What is Promising Here. . . • Create more powerful solvers using concepts from abstract interpretation • Create solvers for new logic fragments Decision Procedures for Logics Satisfiability Modulo Abstraction Symbolic Abstraction • Fundamental technique for working with abstractions Analysis/Verification of Programs • Provides the means for automating abstract interpretation Correct-by-construction analyzers 109
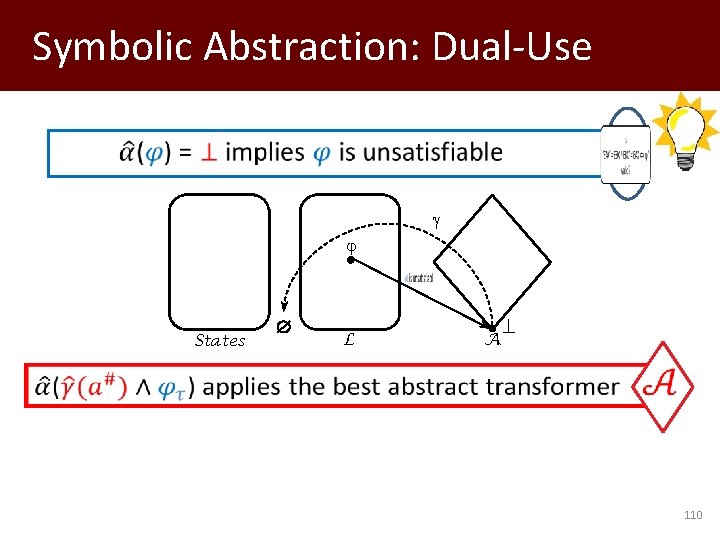
Symbolic Abstraction: Dual-Use States L ⊥ A 110
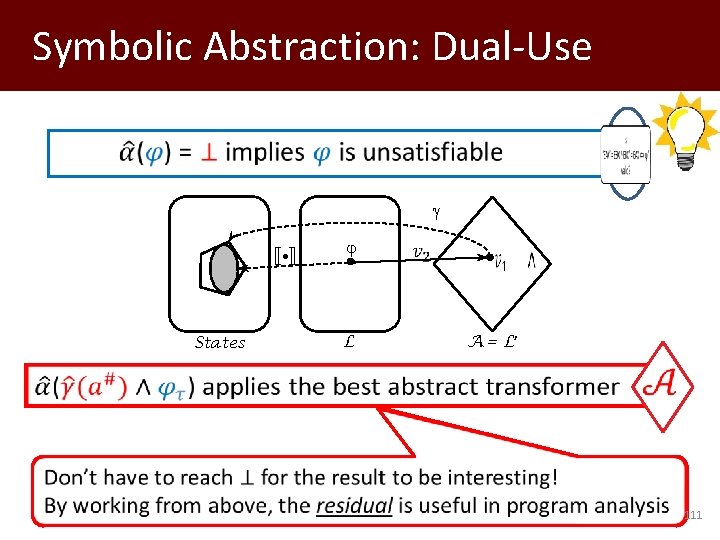
Symbolic Abstraction: Dual-Use States L A = L’ Dagstuhl Seminar 14351 111
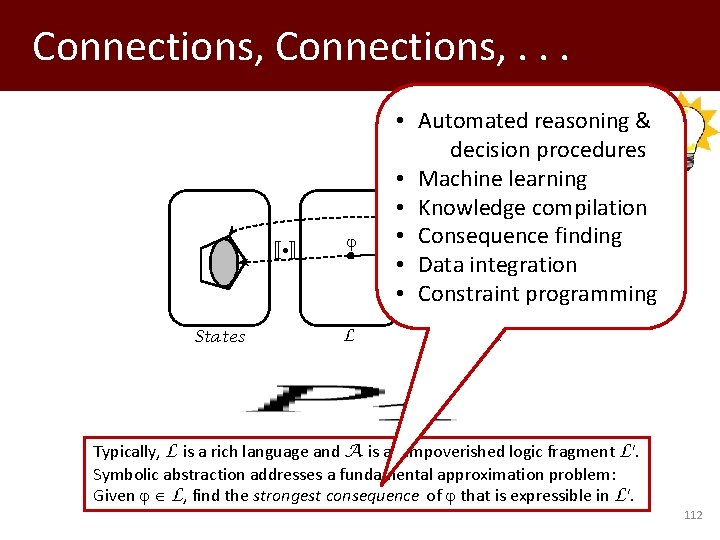
Connections, . . . States L • Automated reasoning & decision procedures • Machine learning • Knowledge compilation • Consequence finding • Data integration • Constraint programming A Typically, L is a rich language and A is an impoverished logic fragment L'. Symbolic abstraction addresses a fundamental approximation problem: Given L, find the strongest consequence of that is expressible in L'. 112
A Plug for. . . A. V. Thakur, Symbolic abstraction: Algorithms and applications , Ph. D. dissertation and Technical Report, Computer Sciences Dept. , University of Wisconsin, Aug. 2014 Aditya Thakur L. C. R. Haller, Abstract satisfaction , Ph. D. dissertation, University of Oxford, 2013 Leo Haller T. Reps and A. Thakur, Automating abstract interpretation. To appear in Proc. VMCAI, Jan. 2016. research. cs. wisc. edu/wpis/papers/vmcai 16 -invited. pdf 113
Automating Abstract Interpretation and Creating Improved Decision Procedures as a Bonus Thomas Reps University of Wisconsin and Gramma. Tech, Inc.
- Slides: 114