Automatic Tuning for Parallel FFTs Daisuke Takahashi University

Automatic Tuning for Parallel FFTs Daisuke Takahashi University of Tsukuba, Japan 2008/6/24 Second French-Japanese PAAP Workshop 1

Outline • • Background Objectives Approach Block Six-Step/Nine-Step FFT Algorithm Automatic Tuning for Parallel FFTs Performance Results Conclusion 2008/6/24 Second French-Japanese PAAP Workshop 2

Background • The fast Fourier transform (FFT) is an algorithm widely used today in science and engineering. • Parallel FFT algorithms on distributedmemory parallel computers have been well studied. • Many numerical libraries with an automatic performance tuning have been developed, e. g. , ATLAS, FFTW, and I-LIB. 2008/6/24 Second French-Japanese PAAP Workshop 3

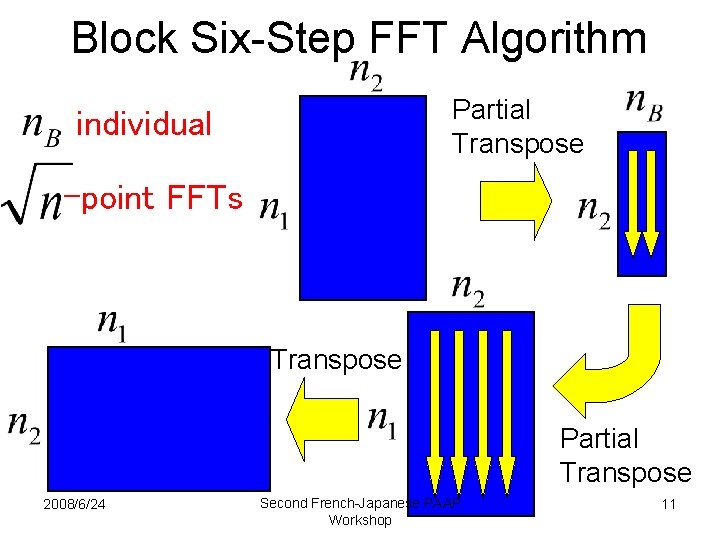
Background (cont’d) • One goal for large FFTs is to minimize the number of cache misses. • Many FFT algorithms work well when data sets fit into a cache. • When a problem exceeds the cache size, however, the performance of these FFT algorithms decreases dramatically. • We modified the conventional six-step FFT algorithm to reuse data in the cache memory. → We will call it a “block six-step FFT”. 2008/6/24 Second French-Japanese PAAP Workshop 4

Related Works • FFTW [Frigo and Johnson (MIT)] – The recursive call is employed to access main memory hierarchically. – This technique is very effective in the case that the total amount of data is not so much greater than the cache size. – For 1 -D parallel MPI FFT, the six-step FFT is used. – http: //www. fftw. org • SPIRAL [Pueschel et al. (CMU)] – The goal of SPIRAL is to push the limits of automation in software and hardware development and optimization for digital signal processing (DSP) algorithms. – http: //www. spiral. net 2008/6/24 Second French-Japanese PAAP Workshop 5

FFTE: A High-Performance FFT Library • FFTE is a Fortran subroutine library for computing the Fast Fourier Transform (FFT) in one or more dimensions. • It includes complex, mixed-radix and parallel transforms. – Shared / Distributed memory parallel computers (Open. MP, MPI and Open. MP + MPI) • It also supports Intel’s SSE 2/SSE 3 instructions. • HPC Challenge Benchmark – FFTE’s 1 -D parallel FFT routine has been incorporated into the HPC Challenge (HPCC) benchmark – http: //www. ffte. jp 2008/6/24 Second French-Japanese PAAP Workshop 6

Objectives • To improve the performance, we need to select the optimal parameters according to the computational environment and the problem size. • We implement an automatic tuning facility for parallel 1 -D FFT routine in the FFTE library. 2008/6/24 Second French-Japanese PAAP Workshop 7

Discrete Fourier Transform (DFT) • DFT is given by 2008/6/24 Second French-Japanese PAAP Workshop 8

2 -D Formulation • If 2008/6/24 has factors and Second French-Japanese PAAP Workshop then 9

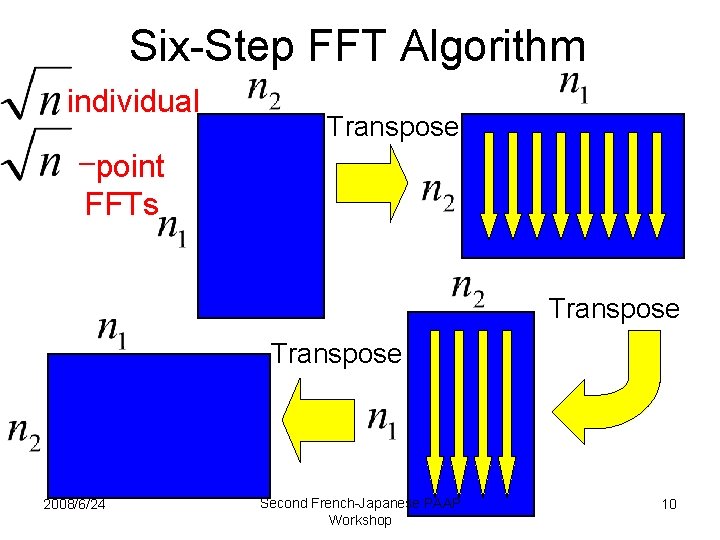
Six-Step FFT Algorithm individual Transpose -point FFTs Transpose 2008/6/24 Second French-Japanese PAAP Workshop 10

Block Six-Step FFT Algorithm Partial Transpose individual -point FFTs Transpose Partial Transpose 2008/6/24 Second French-Japanese PAAP Workshop 11

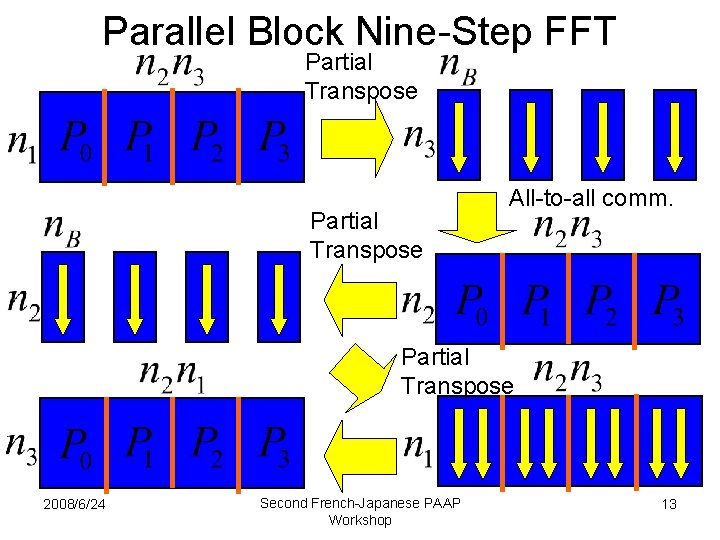
3 -D Formulation • For very large FFTs, we should switch to a 3 -D formulation. • If has factors , 2008/6/24 and Second French-Japanese PAAP Workshop then 12

Parallel Block Nine-Step FFT Partial Transpose All-to-all comm. Partial Transpose 2008/6/24 Second French-Japanese PAAP Workshop 13

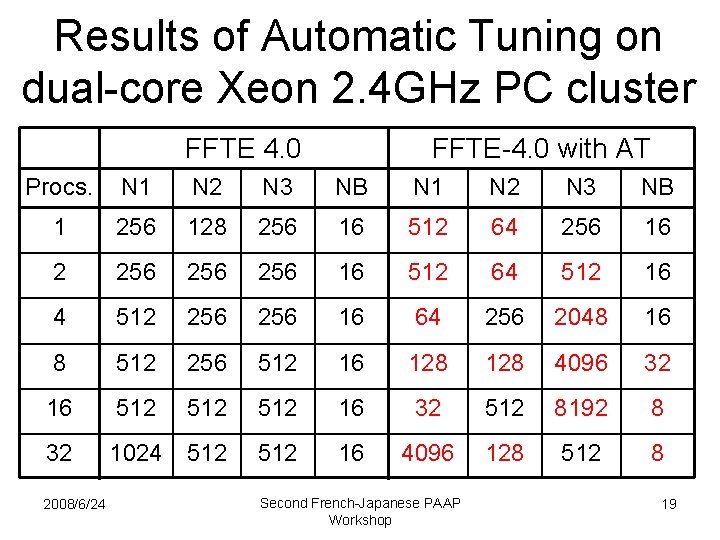
Automatic Tuning for Parallel FFTs • If the condition of we can choose the arbitrary where. is satisfied, then , and , – In the original FFTE library, we chose • The blocking parameter can be also varied. – For a given , the best block size is determined by the L 2 cache size. – In the original FFTE, for Xeon processor. • We implemented the automatic tuning facility for varying , , and. 2008/6/24 Second French-Japanese PAAP Workshop 14

2008/6/24 Second French-Japanese PAAP Workshop 15

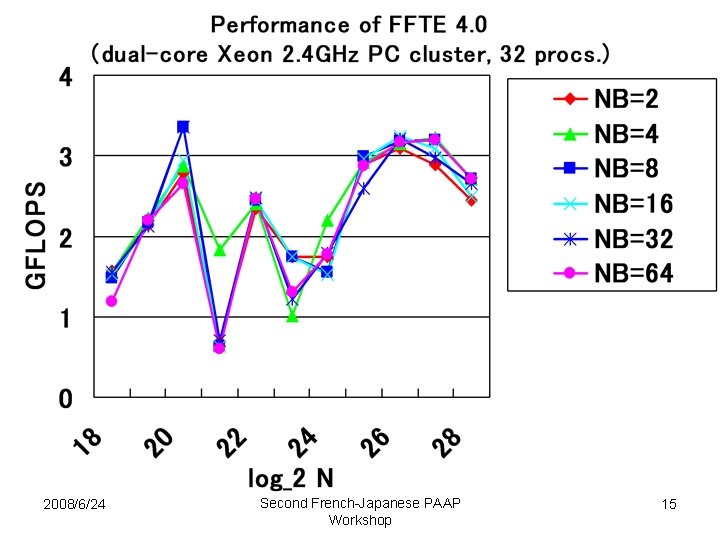
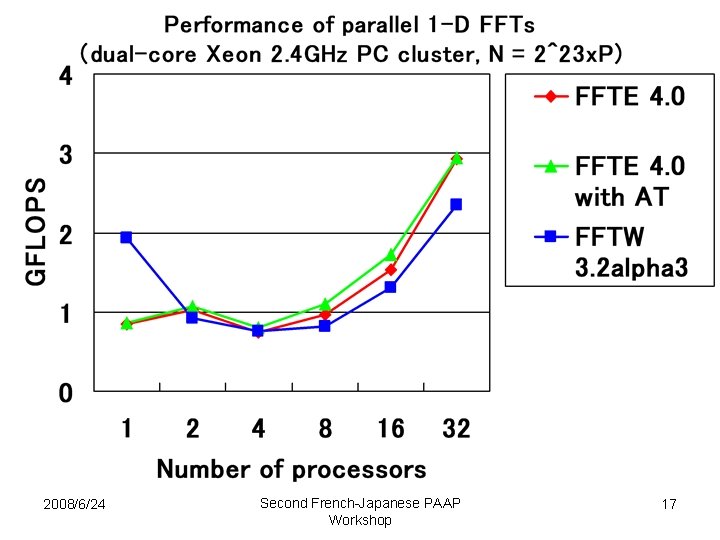
Performance Results • To evaluate parallel 1 -D FFTs, we compared – FFTE (ver 4. 0) with automatic tuning – FFTW (ver. 3. 2 alpha 3) • “mpi-bench” with “PATIENT” planner was used. • Target parallel machine: – A 16 -node dual-core Xeon PC cluster (Woodcrest 2. 4 GHz, 2 GB SDRAM/node, Linux 2. 6. 18). – Interconnected through a Gigabit Ethernet switch. – Open MPI 1. 2. 5 was used as a communication library – The compilers used were Intel C compiler 10. 1 and Intel Fortran compiler 10. 1. 2008/6/24 Second French-Japanese PAAP Workshop 16

2008/6/24 Second French-Japanese PAAP Workshop 17

2008/6/24 Second French-Japanese PAAP Workshop 18

Results of Automatic Tuning on dual-core Xeon 2. 4 GHz PC cluster FFTE 4. 0 FFTE-4. 0 with AT Procs. N 1 N 2 N 3 NB 1 256 128 256 16 512 64 256 16 2 256 256 16 512 64 512 16 4 512 256 16 64 256 2048 16 8 512 256 512 16 128 4096 32 16 512 512 16 32 512 8192 8 32 1024 512 16 4096 128 512 8 2008/6/24 Second French-Japanese PAAP Workshop 19

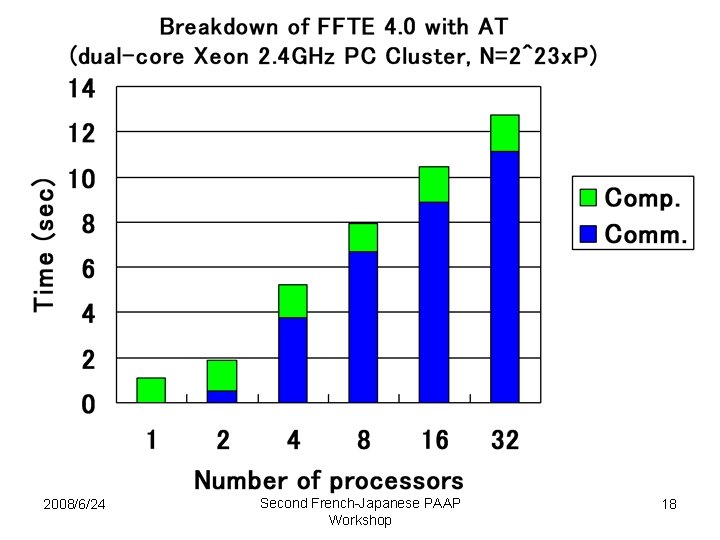
Discussion • For N = 2^28 and P = 32, the FFTE with automatic tuning runs about 1. 25 times faster than the FFTW. – Since the FFTW uses the six-step FFT, each column FFT does not fit into the L 1 data cache. – Moreover, the FFTE exploits the SSE 3 instructions. • These are two reasons why the FFTE is most advantageous than the FFTW. • We can clearly see that all-to-all communication overhead contributes significantly to the execution time. 2008/6/24 Second French-Japanese PAAP Workshop 20

Conclusions • We proposed the automatic tuning method for parallel 1 -D FFTs on distributed-memory parallel computers. • A blocking algorithm for parallel 1 -D FFTs utilizes cache memory effectively. • We found that the default parameters of the FFTE is not always optimal according to the results of the automatic tuning. • The performance of the FFTE with automatic tuning is better than that of the FFTW. 2008/6/24 Second French-Japanese PAAP Workshop 21