Automatic Generation of Staged Geometric Predicates Aleksandar Nanevski

Automatic Generation of Staged Geometric Predicates Aleksandar Nanevski, Guy Blelloch and Robert Harper PSCICO project http: //www. cs. cmu. edu/~pscico

Geometric Predicates • Programs need to test relative positions of points based on their coordinates. • Simple examples (in 2 D): C Orientation test (in convex hull) B does C lie left/right/on the line AB? A Incircle test (in Delaunay triangulation) does D lie in/out/on the circle ABC? D A C B 2

Geometric Predicates (cont’d) • Orientation(A, B, C) = • We only consider the sign of an expression involving +, - and £ 3

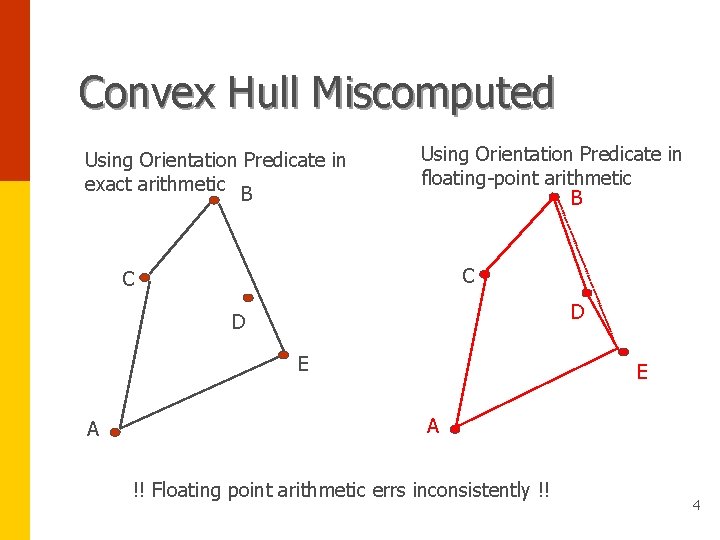
Convex Hull Miscomputed Using Orientation Predicate in exact arithmetic B Using Orientation Predicate in floating-point arithmetic B C C D D E A !! Floating point arithmetic errs inconsistently !! 4

Floating-point Filters • Get correct sign (-1, 0 or 1) of an exact expression E using floating-point! “filters out” the easy cases let F = E (X) in floating point if F > error bound then 1 else if –F > error bound then – 1 else increase precision and repeat or switch to exact arithmetic • If the correct result is 0, must go to exact phase 5

Current Methods • Interval arithmetic (R. E. Moore, U. Kulisch) +little modification to the source program -does not perform well in low degrees • Single-phase filters (Fortune & Van Wyk, LEDA) +compiler available -surpassed by multi-phase filters 6

Current Methods (cont’d) • Multi-phase filters (J. Shewchuk) • four phases of increasing precision +re-use of results from earlier phases +between 8 -35% slower than fp implementation -requires estimating rounding errors -involved and hard to implement: Shewchuk’s Insphere C implementation >500 lines of code -only existing are 2 D and 3 D Orientation and Insphere predicates, but we need more 7

Functional program COMPILER numerical analysis Staged geometric predicate 8

Contributions • Source language • expression involving +, -, £ • arithmetic to be perceived as exact • nested anonymous functions (staging) • Compiler to ML (or C) • multi-phase target code • error bounds estimated automatically • formally specified (so, can argue correctness) 9

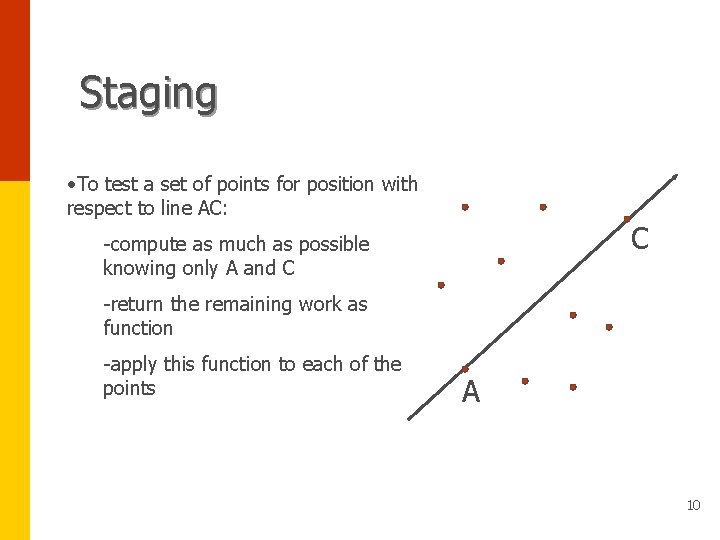
Staging • To test a set of points for position with respect to line AC: C -compute as much as possible knowing only A and C -return the remaining work as function -apply this function to each of the points A 10

Overview • Introduction • Arbitrary precision arithmetic and computing in phases • Stage compilation • Performance • Conclusions and Future Work 11

Notation • Operations: Exact + Floating point © - ª £ • Precision p = #bits in mantissa • Machine Epsilon if operation result is 1. 0, then the rounding error is smaller than - 12

Error recovery Theorem. (Knuth) If x = a © b, the rounding error of x can be recovered by floating-point operations. If D is the rounding error, and c = x ª a then So exactly. 13

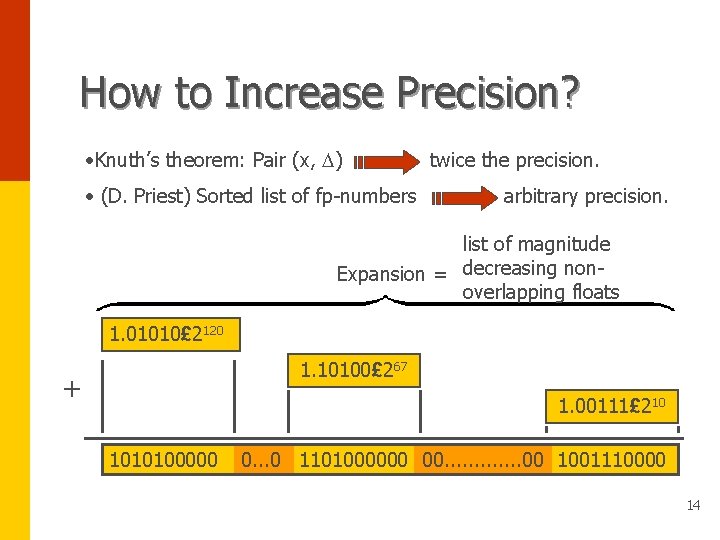
How to Increase Precision? • Knuth’s theorem: Pair (x, D) • (D. Priest) Sorted list of fp-numbers twice the precision. arbitrary precision. list of magnitude Expansion = decreasing nonoverlapping floats 1. 01010£ 2120 1. 10100£ 267 + 1. 00111£ 210 1010100000 0. . . 0 1101000000 00. . . 00 1001110000 14

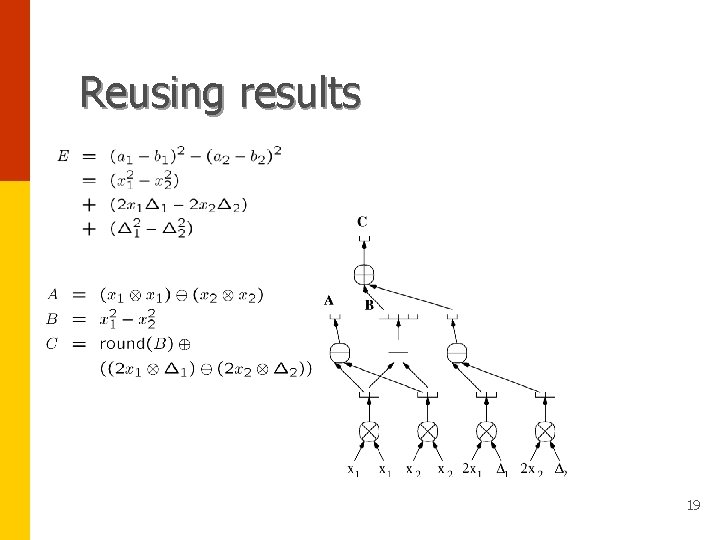
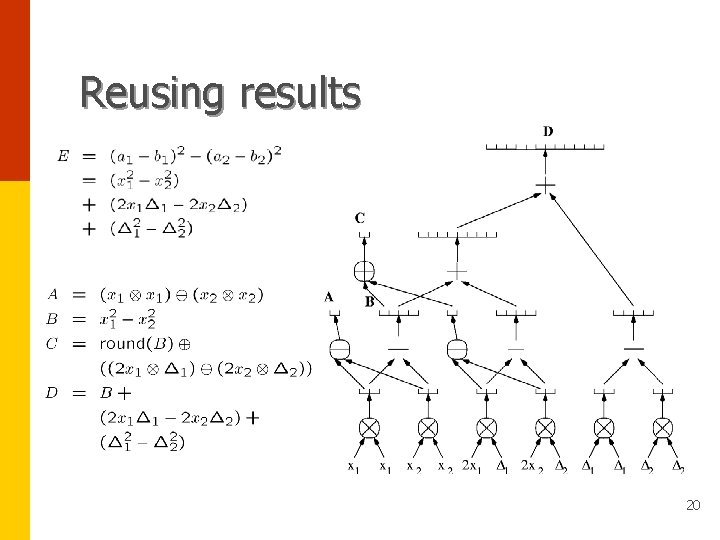
Phases and re-use • (J. Shewchuk) Arbitrary precision arithmetic reuse the results of their predecessors. phases can Example: Let a 1 – b 1 = x 1 + D 1 and a 2 – b 2 = x 2 + D 2. Expand E as 15

Phases and re-use (cont’d) • Strategy for finding the sign of • Evaluate E in phases, increasing precision on demand. • Example: floating point phase exact phase 16

Reusing results 17

Reusing results 18

Reusing results 19

Reusing results 20

Overview • Introduction • Arbitrary precision arithmetic and computing in phases • Stage compilation • Performance • Conclusion and Future Work 21

Source Language • Basic arithmetic operations: +, -, £, unary -, sq • Assignments: val x = some expression • Nested anonymous functions • Example: • Implicit sign test at the last assignment. 22

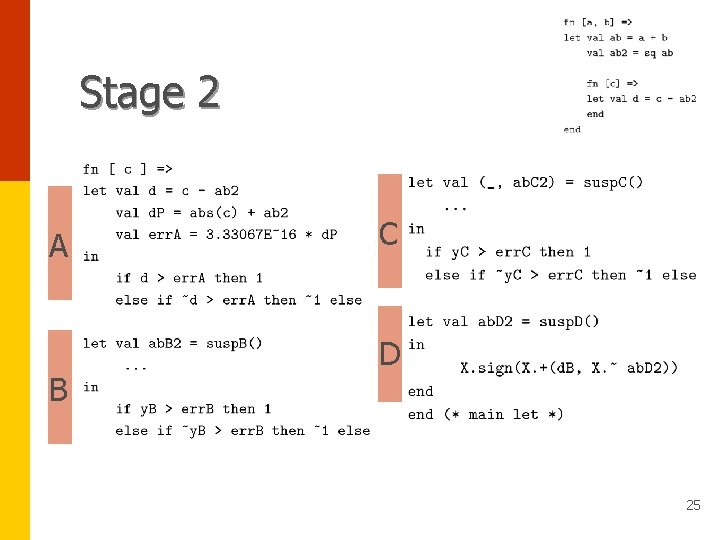
Stage compilation • Every stage compiled into: -floating-point code (phase A) -code for estimating the rounding error • Later phases (B, C and D) “suspended” until explicitly executed 23

Stage 1 • Helper code: -modules for arbitrary precision arithmetic • Compiler output: A B C D 24

Stage 2 A B C D 25

Overview • Introduction • Arbitrary precision arithmetic and computing in phases • Stage compilation • Performance • Conclusion and Future Work 26

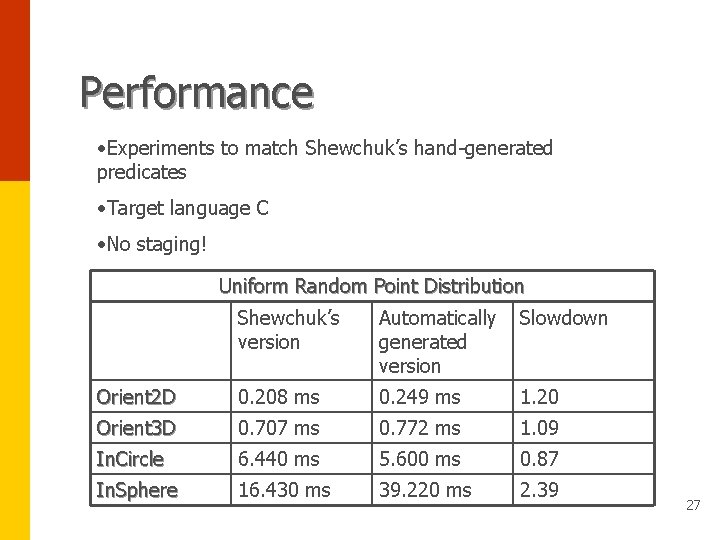
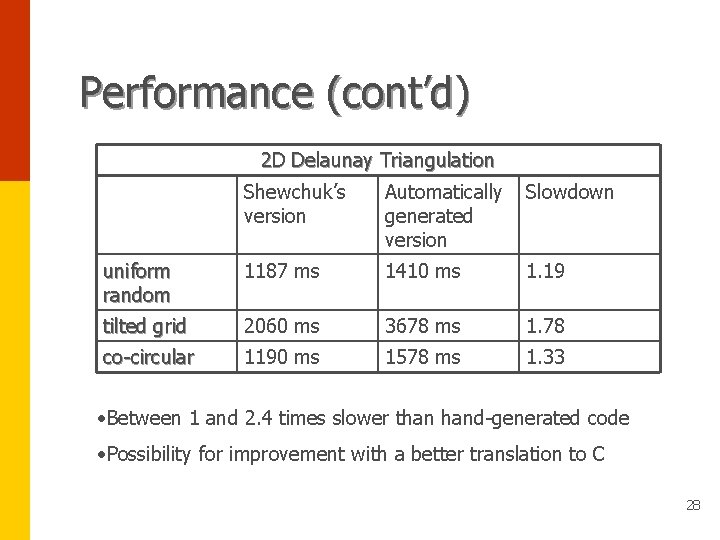
Performance • Experiments to match Shewchuk’s hand-generated predicates • Target language C • No staging! Uniform Random Point Distribution Shewchuk’s version Automatically generated version Slowdown Orient 2 D 0. 208 ms 0. 249 ms 1. 20 Orient 3 D 0. 707 ms 0. 772 ms 1. 09 In. Circle 6. 440 ms 5. 600 ms 0. 87 In. Sphere 16. 430 ms 39. 220 ms 2. 39 27

Performance (cont’d) 2 D Delaunay Triangulation Shewchuk’s version Automatically generated version Slowdown uniform random 1187 ms 1410 ms 1. 19 tilted grid 2060 ms 3678 ms 1. 78 co-circular 1190 ms 1578 ms 1. 33 • Between 1 and 2. 4 times slower than hand-generated code • Possibility for improvement with a better translation to C 28

Future Work • Extend the language: -multiplication by 2 n doesn’t introduce errors. -summation of more than 2 elements can be done quicker. • Evaluate the effects of staging. • Allow better control over the FP arithmetic in SML. - processor flags - precision of internal FP registers • Design a language that can compile and run the predicates - run-time code generation and meta-programming - application: robust solid modeler 29

Conclusions • Automated conversion of exact predicates into floating point code: • preserves correctness of computation despite rounding • compile-time error analysis • nested anonymous functions (staging) • performance of generated predicates close to hand-generated code • Formal specification of the compiler. • More control needed over floating point in SML. -processor flags -precision of internal FP registers • Compiler can be found at http: //www. cs. cmu. edu/~pscico 30

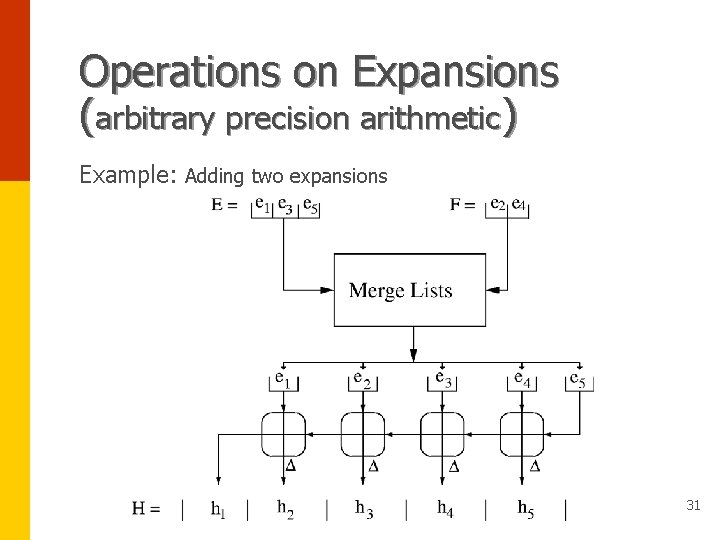
Operations on Expansions (arbitrary precision arithmetic) Example: Adding two expansions 31

Source Language • Basic arithmetic operations: +, -, £, sq, unary – • Assignments: val x = some expression • Nested anonymous functions (staging) 32

Compiling a Program C A D B 33

Compiling a Program (cont’d) reused A 34

Here goes example for Orient 2 D in SML or C Nothing! They are just often mistaken for real numbers. type pnt=real*real fun orient(A: pnt, B: pnt, C: pnt)= let val (a 1, a 2) = A val (b 1, b 2) = B val (c 1, c 2) = C val d = (c 1 -a 1)*(c 2 -b 2) (c 2 -a 2)*(c 1 -b 1) in if d > 0 then Left else if d < 0 then Right else On end 35

What’s Wrong With Floating Point Numbers? Floats are unevenly distributed on the real axis, thus introducing rounding errors in the computation. 36

What’s Wrong? (cont’d) Example: Assume precision of 2 decimal digits. Denote © the operation of (rounded) addition on floats. Floats are a subset but NOT a subtype of rationals and reals. 37

Types of Numbers Real numbers + - Usually assumed when developing or proving algorithms Rational numbers + Closed under basic operations - Slow Basic operations not computable Floating-point numbers + Fast - Not closed under basic arithmetic operations (rounding errors) - Do not satisfy usual laws like associativity, distributivity 38

Phase A Compilation • Judgment . • Selected rules 39

Phase B Compilation • Judgment . • Selected rules 40

Operations on Expansions Example: Adding a double to an expansion. 41

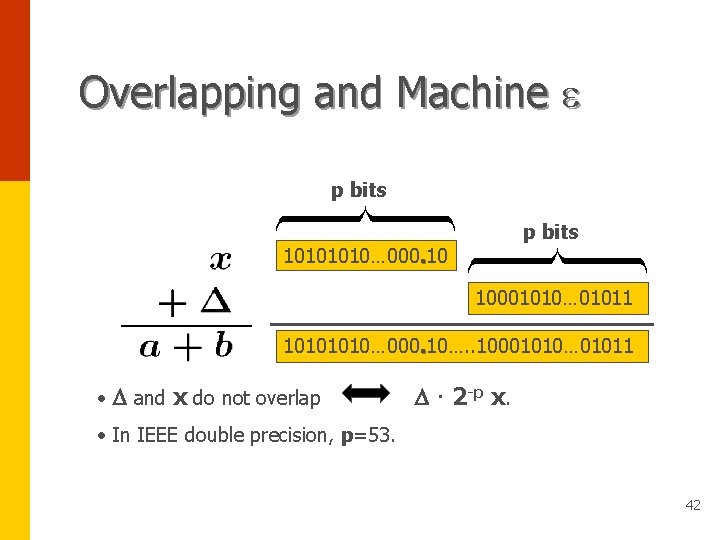
Overlapping and Machine e p bits 1010… 000. 10 10001010… 01011 1010… 000. 10…. . 10001010… 01011 • D and x do not overlap D · 2 -p x. • In IEEE double precision, p=53. 42

Phases of Increasing Precision let R = F (X) in floating point if abs(R) > estimated error bound then sign(R) else increase precision and repeat or switch to exact arithmetic floating point phase intermediate phases exact phase • Finitely many intermediate phases! 43

Arithmetic Rational numbers + exact Floating-point numbers - slow - inexact + fast 44

Non-overlapping • The rounded sum x and its rounding error D do not overlap. 1010… 000. 10 0000…………… 0. 00 10001010… 01011 1010… 000. 10…. . 10001010… 01011 • Mathematically, 45

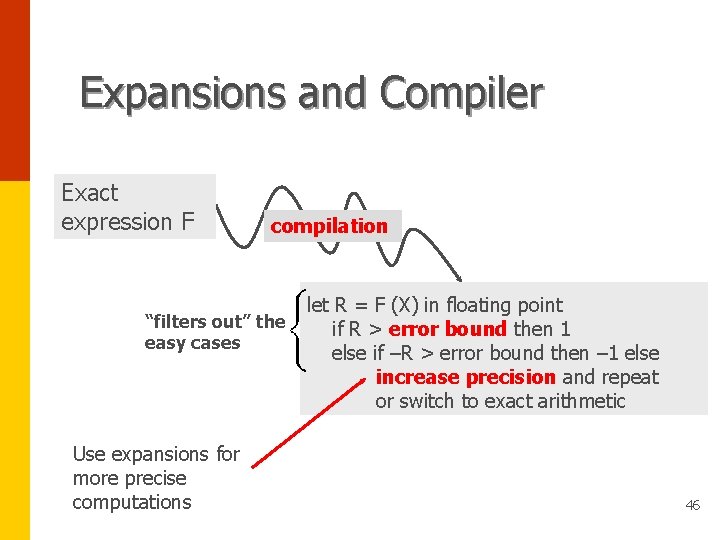
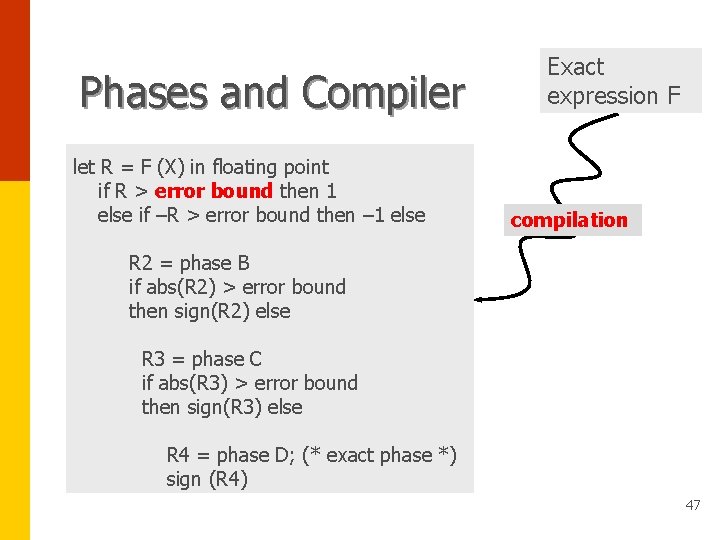
Expansions and Compiler Exact expression F compilation “filters out” the easy cases Use expansions for more precise computations let R = F (X) in floating point if R > error bound then 1 else if –R > error bound then – 1 else increase precision and repeat or switch to exact arithmetic 46

Phases and Compiler let R = F (X) in floating point if R > error bound then 1 else if –R > error bound then – 1 else Exact expression F compilation R 2 = phase B if abs(R 2) > error bound then sign(R 2) else R 3 = phase C if abs(R 3) > error bound then sign(R 3) else R 4 = phase D; (* exact phase *) sign (R 4) 47

Bounding the Rounding Error • Floating-point operations are correctly rounded. • Consequence: for any operation ¢ 2 {+, -, £} • Notice: e is static part of the error while |x ¯ y| is dynamic. 48

Bounding Error of Composite Expressions • If X 1 = x 1 § d 1 p 1 and X 2 = x 2 § d 2 p 2 then 49

Error Bounds and Compilation • Static error bound - Obtained EXACTLY in compile-time. - Rounded and then emitted into the target program as a floating-point constant. • Dynamic error bound - Code must be generated for its computation and emitted into the target program. 50

Error Bounds and Compilation (cont’d) compilation Exact expression F let R = F (X) in floating point dynamic_error = D (X) error = static_error * dynamic_error if R > error then 1 else if –R > error then – 1 else jump to phases B, C and D 51

Compilation example • Source expression c – (a + b)2 • Target Standard ML program: 52

Source Language • Basic arithmetic operations: +, -, £, sq, unary • Assignments: val x = some expression • Nested anonymous functions 53

Staging (cont’d) 54

Overview • Introduction • Arbitrary precision arithmetic and computing in phases • Multi-stage filters • Performance • Conclusion and Future Work 55