Automatic generation of optimized working time models in

Automatic generation of optimized working time models in personnel planning TU Ilmenau Department of Commercial Information Technology for Services (WI 2) 1 Dipl. Wirt. -Inf. Maik Günther maik. guenther@gmx. de Prof. Dr. Volker Nissen volker. nissen@tu-ilmenau. de

• Description of the Application Problem • Particle Swarm Optimization • Evolution Strategies • Results and Conclusion 2 Structure of presentation

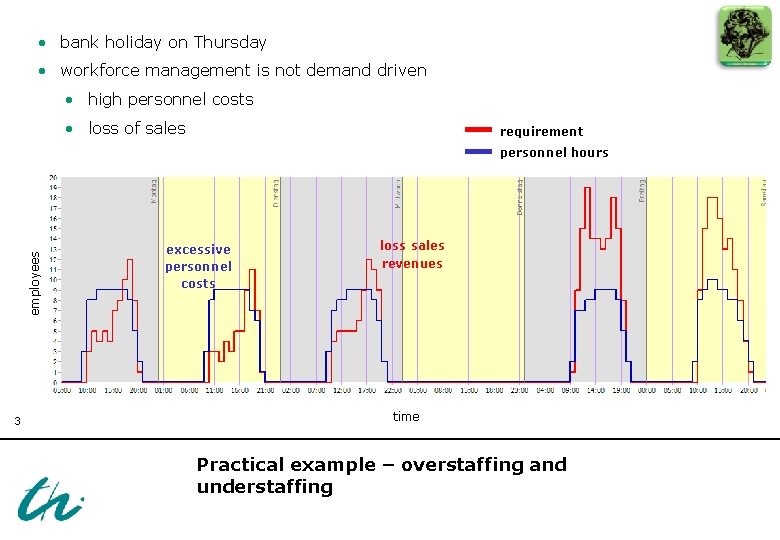
• bank holiday on Thursday • workforce management is not demand driven • high personnel costs • loss of sales requirement employees personnel hours 3 excessive personnel costs loss sales revenues time Practical example – overstaffing and understaffing

• department of a store (clothes) • each day 10 hours (from Monday to Saturday) • 15 employees with different contracts (weekly working time 10, 25, 30, 38 and 40 hours) • 2 workplaces (sales and cash register) • variable customer frequency during the day variable personnel demand with large variations for individual workstations during the day • demand is given in 1 -hour intervals for 1 year Create a rooster with automated generated working time models! 4 Application problem

• hard constraints • only available employees are scheduled • only one workstation per employee at a time • working time models in 1 -hour intervals • soft constraints (error points): • only one or no working time model per employee a day • keep minimal/maximal allowed length of working time models • avoid over- and understaffing • avoid unnecessary workstation rotations • employees should not work more than their maximal working time per week 5 Input and constraints

• problems in retailing with automated generated working time models • but only 1 workstation • some differences in constraints • smaller planning horizon • Prüm [9] was not able to solve the MIP in reasonable time solved the relaxed LP and transformed the result (real values) to a solution (integer values) • Sauer and Schumann [10] uses a constructive heuristic 6 Work related to the application problem

• numbers • 0: store is closed / employee is not available • 1 -2: correspond to workstations • 3: dummy workstation (employee is not working) • based on two-dimensional matrix • time is viewed as discrete • 8. 760 rows and 15 columns = 131. 400 dimensions • Garey and Johnson demonstrate that even simple versions of staff scheduling problems are NP-hard [6]. 7 • Kragelund and Kabel show the NP-hardness of the general employee timetabling problem [8]. Problem representation for PSO and ES

• Description of the Application Problem • Particle Swarm Optimization • Evolution Strategies • Results and Conclusion 8 Structure of presentation

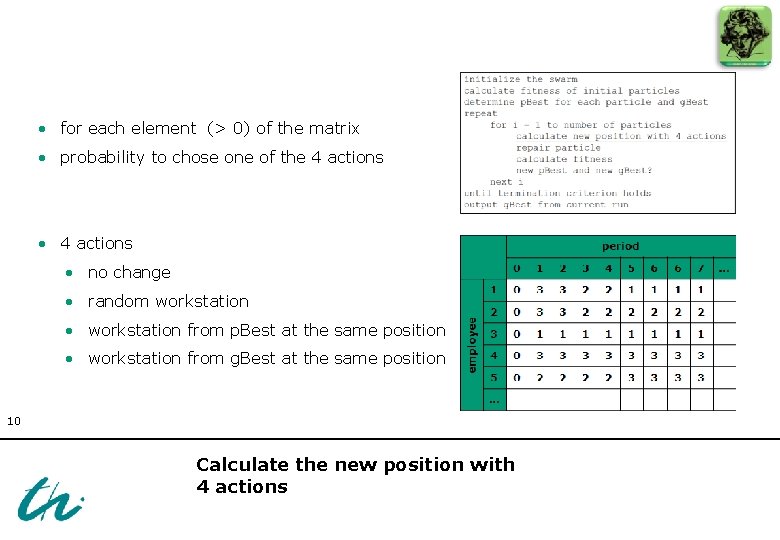
• initialize population-based modern heuristic the swarm • calculate swarm members are assumed to be massless particles fitness of initial particles each particle and g. Best • determine each particle p. Best together for with its position within a solution space repeat embodies a solution to the problem for ifor= optima 1 to with number • they search the aidof of aparticles fitness function calculate new position with 4 actions • particles exchange information, which can positively influence the repair particle development of the population as a whole (p. Best, g. Best/l. Best) calculate fitness new p. Best and new g. Best? next i until termination criterion holds output g. Best from current run • termination of PSO after 400. 000 inspected solutions (to keep results comparable) 9 Overall outline of PSO approach

• for each element (> 0) of the matrix • probability to chose one of the 4 actions • 4 actions • no change • random workstation • workstation from p. Best at the same position • workstation from g. Best at the same position 10 Calculate the new position with 4 actions

• Description of the Application Problem • Particle Swarm Optimization • Evolution Strategies • Results and Conclusion 11 Structure of presentation

• initialize each individualthe of thepopulation embodies a solution to the problem calculate fitness of initial population • repeat they search for optima with the aid of a fitness function draw andoperator recombine parent • primarily search is mutation solutions mutateofoffspring • self-adaption mutation step size repair offspring • each individual has a strategic parameter which will be mutated calculate fitness for offspring and recombined select the new population • higher probability for individuals with a good strategic parameter until termination criterion holds to survive output best solution from current run 12 • termination of ES after 400. 000 inspected solutions (to keep results comparable) Overall outline of evolutionary approach

• selection • deterministic, non-elitist comma- and plus-selection • following suggestions in the literature [2] [3], the ratio μ/λ is set to 1/5 – 1/7 • (1, 5), (1+5), (10, 50), (10+50), (30, 200) and (30+200) • best solution kept in “golden cage” (not part of population) • recombination of two parent solutions ((10, 50), (10+50), (30, 200), (30+200)) • one random crossover point for all employees parent 1 parent 2 offspring 13 Draw and recombine parent solutions & select the new population

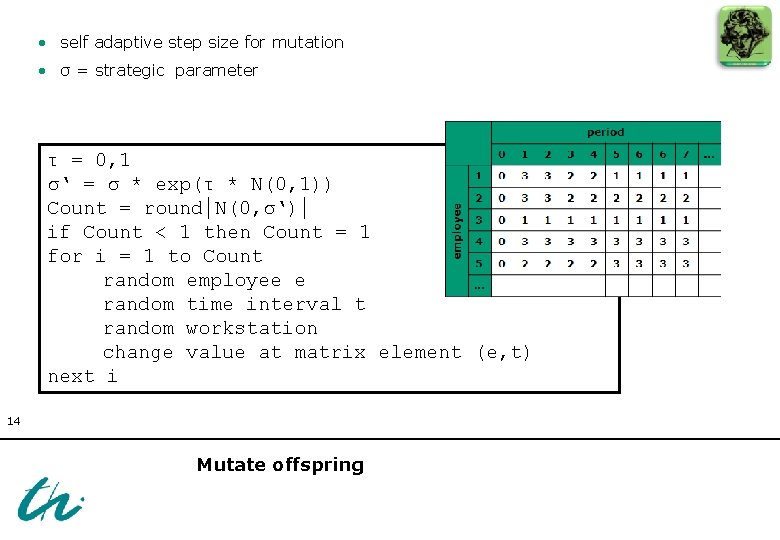
• self adaptive step size for mutation • σ = strategic parameter τ = 0, 1 σ‘ = σ * exp(τ * N(0, 1)) Count = round│N(0, σ‘)│ if Count < 1 then Count = 1 for i = 1 to Count random employee e random time interval t random workstation change value at matrix element (e, t) next i 14 Mutate offspring

• Description of the Application Problem • Particle Swarm Optimization • Evolution Strategies • Results and Conclusion 15 Structure of presentation

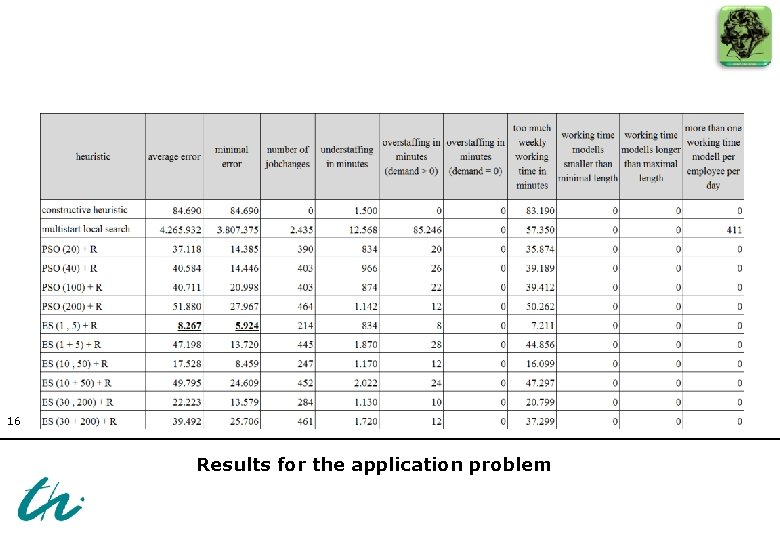
16 Results for the application problem

• ES-approach with (1, 5)-selection and repair is the most effective heuristic for this problem • plus-selection often get stuck in local optima • comma-selection has a higher ability to escape from local optima explore other regions (with worse results over some generations on the way to other regions) • PSO is easy to use (2 important parameters swarm size and probability to set a random workstation) • make small changes in one iteration/generation • future research • create further test problems with the aid of cooperating companies 17 • adapt other heuristics from roughly comparable problems in the literature Conclusions

18 Data sets and benchmarks

1. Bäck T. (2002) (ed. ) Handbook of Evolutionary Computation. Institute of Physics Publishing, Bristol 2. Beyer H. -G. , Schwefel, H. -P. (2002) Evolution strategies: a comprehensive introduction. Nat. Comp. 1: 3 -52 3. Chu S. C. , Chen Y. T. , Ho J. H. (2006) Timetable Scheduling Using Particle Swarm Optimization. In: Proceedings of ICICIC Beijing 2006, Vol. 3: 324 -327 4. Brodersen O. , Schumann M. (2007) Einsatz der Particle Swarm Optimization zur Optimierung universitärer Stundenpläne. Technical Report 05/2007, Univ. of Göttingen 5. Ernst A. T. , Jiang H. , Krishnamoorthy M. , Owens B. , Sier D. (2002) An Annotated Bibliography of Personnel Scheduling and Rostering. Annals of OR 127: 21 -144 6. Garey M. R. , Johnson D. S. (1979) Computers and Intractability. A Guide to the Theory of NPCompleteness 7. Kennedy J. , Eberhart R. C. , Shi Y. (2001) Swarm Intelligence. Kaufmann, San Francisco 8. Kragelund L. , Kabel T. (1998) Employee Timetabling. An Empirical Study, Master's Thesis, Univ. of Aarhus 9. Prüm H. (2006) Entwicklung von Algorithmen zur Personaleinsatzplanung mittels ganzzahliger linearer Optimierung. Master's Thesis, FH Trier 10. Sauer J. , Schumann R. (2007) Modelling and Solving Workforce Scheduling Problems. in: Sauer J. , Edelkamp S. , Schattenberg (ed. ): Proceedings of the 21 th Pu. K 2007: 93 -101. 19 11. Tien J. , Kamiyama A. (1982) On Manpower Scheduling Algorithms, SIAM Rev. 24(3): 275287 References