Automated Search for Conserved Quantities in Particle Reactions

Automated Search for Conserved Quantities in Particle Reactions Oliver Schulte School of Computing Science Simon Fraser University oschulte@cs. sfu. ca SFU Particle Physics Group

Outline What’s this about? Finding conserved quantities in particle reactions n n n Algorithm Data Findings Introducing extra particles to fit the data better SFU Particle Physics Group 2

CS Goals • Basic research (good enough): Write programs that match theories from physics. • Previous work: • Kobacas, Valdes-Perez on discovering selection rules. • Valdes-Perez, Zytkow on (re)discovering particle substructure (Physical Review E, 1996) • Practical use (icing on the cake): analyze data to help with new discoveries. SFU Particle Physics Group 3

The Goal: Find Absolutely Conserved Quantities Omnes (1971), Introduction to Particle Physics. “The method [of assigning quantum numbers] is rather lengthy … so that we give the procedure in detail, once and for all. ” Want a program for assigning quantum numbers. SFU Particle Physics Group 4

Basic Principle: Disallow as much as you can • Leon Cooper (1970). “In the analysis of events among these new particles, where the forces are unknown and the dynamical analysis, if they were known, is almost impossibly difficult, one has tried by observing what does not happen to find selection rules, quantum numbers, and thus the symmetries of the interactions that are relevant. ” • Kenneth Ford (1965). “Everything that can happen without violating a conservation law does happen. ” SFU Particle Physics Group 5

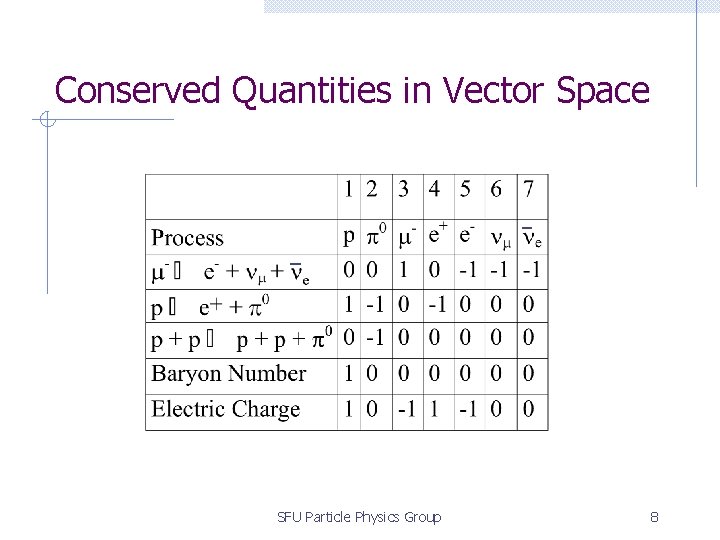
How much can we rule out? Hypothetical Scenario observed reactions - - + n - m- + n m m- e - + n m + n e n e- + ne + p p+p+ not yet observed reactions n e- + ne p+p+ + can’t rule out SFU Particle Physics Group 6

The Vector Representation for Reactions • Fix n particles. • Reaction n-vector: list net occurrence of each particle. SFU Particle Physics Group 7

Conserved Quantities in Vector Space SFU Particle Physics Group 8

Conserved Quantities are in the Null Space of Observed Reactions Let q be the vector for a quantum number, r for a reaction. Then q is conserved in r q r = 0. Let Q be a matrix of quantities. Then Qr = 0 r is allowed by Q. So: if r 1, …, rk are allowed, so is any linear combination. SFU Particle Physics Group 9

Maximally strict selection rules = basis for nullspace of observations • Defn: A list of selection rules Q is maximally strict nullspace(Q) = span(R). • Proposition: Q is maximally strict span(Q) = R. SFU Particle Physics Group 10

System for Finding a Maximally Strict Set of Selection Rules Read in Observed Reactions Convert to list of vectors R Compute basis Q for nullspace R SFU Particle Physics Group from database using conversion utility Maple function nullspace 11

The Data: Particles • Particles from Review of Particle Physics • Total 193 particles • Separate entries for particle and antiparticles • e. g. , p, p = 2 entries • One entry for same type, different masses • e. g. , just one entry for Σ(1385), Σ(1670) SFU Particle Physics Group 12

The Data: Reactions • At least one decay for each particle with a decay mode. • Particle utility converts to vector representation. SFU Particle Physics Group 13

Why Decays? Wanted: linearly independent reactions. Proposition: Decays of distinct particles are linearly independent. SFU Particle Physics Group 14

# independent quantities # unstable particles Defn. A particle is stable if it has no decay mode, e. g. , Proposition Fix n particles, allowed reactions R. 1. dim(R ) n - # unstable particles 2. # independent conserved quantities # stable particles • e. g. n = 193 particles, 11 stable 11 conserved quantities • because of antiparticles, can be improved to 6 conserved quantities SFU Particle Physics Group 15

Finding #1 {Baryon#, E. Charge, Muon#, Electron#, Tau#} is basis for nullspace of possible reactions. 1. Output of Program is equivalent classifier to standard rules. 2. All absolutely conserved quantum numbers are linear combinations of {Baryon#, E. Charge, Muon#, Electron#, Tau#} e. g. , Lepton# = Muon# + Electron# + Tau# SFU Particle Physics Group 16

Finding #2 Program matches particle-antiparticle pairings. There is an analytic explanation. SFU Particle Physics Group 17

Finding #3 Different runs seem to produce version of the lepton family laws e. g. , {- Muon#, - Electron#, -Tau#}. No analytic explanation. SFU Particle Physics Group 18

More Particles can lead to stricter Conservation Principles Well-known example: if e = e, then n + n p + e- should be possible. (Williams Ch. 12. 2). SFU Particle Physics Group 19

When do more particles lead to stricter Conservation Principles? Theorem An extra particle yields stricter selection rules for a set of reactions R there is a reaction r such that 1. r is a linear combination of R 2. but only with fractional coefficients. SFU Particle Physics Group 20

Hidden Particles, Finding #1 The standard selection rules are maximally strict with respect to transitions among nonneutrinos. SFU Particle Physics Group 21

Critical Reaction for e e Discovered by Computer Finding if e = e , then the process Υ + Λ 0 p + ecannot be ruled out with selection rules. SFU Particle Physics Group 22

Conclusions Program computes maximally strict set of selection rules. Good match with {Baryon#, E. Charge, Muon#, Electron#, Tau#} n n Classifies reactions as possible or impossible in exact agreement. Reproduces particle-antiparticle pairings Extra particle: Computes a critical experiment to test if e = e. SFU Particle Physics Group 23

Further Work Search for partially conserved quantities like strangeness. Historical Analysis of Data (R. Coleman). Pitch: looking for coauthor/proofreader for interdisciplinary or physics publication. SFU Particle Physics Group 24