Automated Map Labeling with an introduction to computability

Automated Map Labeling with an introduction to computability, computational complexity, and evolutionary algorithms Wan Bae (Computer Science, University of Denver) Sada Narayanappa (Jeppesen) Petr Vojtěchovský (Mathematics, University of Denver) are working on the problem is merely talking about it

Map Labeling = association of labels to geographic entities point features (restaurants) l line features (streets) l boundaries (state parks) l We focus on point features.

Why automate? l l l manual resolution of conflicts is time consuming most conflicts can be resolved by simple heuristics labeling rules easily enforced

Parameters of labels font size and type l relative position of labels and sites l proximity to other labels and sites l esthetic preference/tradition l

How difficult is “Map labeling”? NP-complete difficult! We (=mankind) think that’s very difficult! But we really don’t know!

What is computation? We don’t know. Church-Turing thesis: Computation is precisely what can be performed with a universal Turing machine. tape with symbols (0, 1, B) current state head Depending on the state and symbol: - rewrite symbol - move head left or right - change state - stop when an “end-state” is reached

How realistic are Turing machines? l l universal Turing machine is a TM that can emulate any other Turing machine universal Turing machines exist digital computers (with potentially unlimited memory and storage) are UTMs we don’t know of any process in nature that resembles computation and is not done on a TM

Algorithm = TM Algorithm is a finite list of well-defined instructions for accomplishing some task that, given an initial state, will terminate in a defined end-state. Read: list of instructions = description of TM initial state = input tape end-state = what’s on the tape when TM stops

Can all problems be solved with UTM? No! Here is a problem that cannot be solved: Halting problem: Given a Turing machine T and an input tape I, will T eventually stop when started with I?

Complexity of computation Let A be an algorithm (=TM). A(n) = max running time of A on an input of length n We are interested in the behavior of A(n) for large n. More precisely: We need to find a function f(n), such as log(n), n 2, exp(n), for which the limit of A(n)/f(n) as n approaches infinity is equal to 1.

Hierarchy of complexities Depending on f(n), the algorithm is: l l l polynomial, P, if f(n) is a polynomial in n exponential, if f(n) is an exponential function of n logarithmic, linear, … Example: Addition of two n-digit numbers takes about n steps, hence the usual addition algorithm is linear. Example: Factorization of integers into primes … … the complexity is not known. (RSA & Internet security? )

The class NP We don’t know complexities for most algorithms; we might only have lower and upper estimates. A problem is NP (non-deterministic polynomial) if once a solution is presented, it requires no more than polynomial time to verify that the solution is correct. The biggest open problem in CS ($1, 000): Is NP=P? A more lucrative problem ($4, 000): Be the first one to solve Eternity II.

The class NP-complete A problem X is NP-complete if: l l X is NP, for every problem Y in NP, it is possible to translate input y for Y into an input x for X in polynomial time, so that the solution to Y with y is the same as the solution to X with x. Briefly, X is at least as hard as any NP problem.

3 -SAT is NP-complete problems exist!!! 3 -SAT problem: Given a logical condition of the form (A or B or C) and (D or E or F) and …, where each of A, B, C, … is a variable or a negation of a variable, is it possible to assign values TRUE or FALSE to the variables so that the condition evaluates as TRUE?

Traveling salesman is NP-complete A graph is a bunch of points (vertices) connected by lines (edges). A graph has a Hamiltonian cycle if it is possible to visit all of its vertices and return to the starting vertex without using any edge more than once. Traveling salesman problem: Does a given graph have a Hamiltonian cycle?

Map labeling is NP-complete … even in these situations: l l determine if a labeling exists with no overlaps as above, with all labels the same find an optimum labeling (allow overlaps) determine if at least 50% of labels can be positioned without overlaps It is therefore reasonable to resort to: l l approximate (non-optimal) solutions heuristics (algorithms driven by educated guesses)

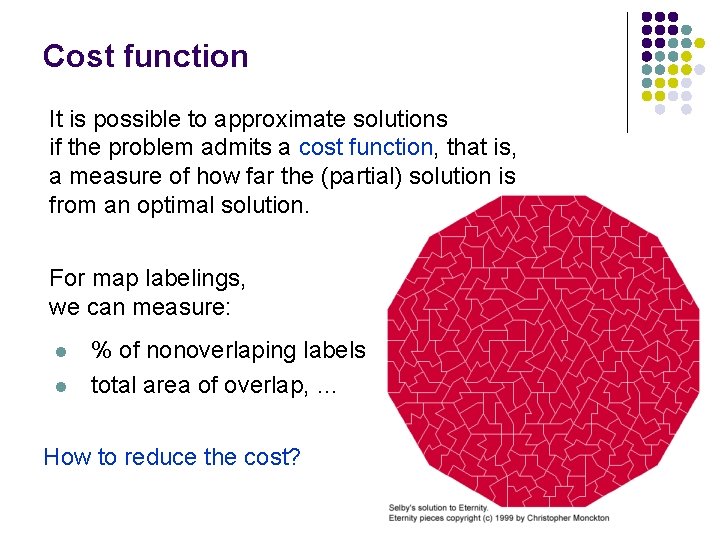
Cost function It is possible to approximate solutions if the problem admits a cost function, that is, a measure of how far the (partial) solution is from an optimal solution. For map labelings, we can measure: l l % of nonoverlaping labels total area of overlap, … How to reduce the cost?

Reducing cost: Divide and conquer 1) split the problem into smaller ones 2) solve the smaller problems 3) piece the large solution together Example: QUICKSORT, has complexity n log(n) For map labelings, 1) and 2) are easy. 3) is hard.

Reducing cost: Evolutionary algorithms 1) From a current situation, evolve many similar situations by small modifications (mutations) 2) 2) Pick the best offspring and kill other children. 3) 3) Kill the parent if the surviving child is better. 4) Example: stock market software If the situation is based on a “DNA”, evolutionary algorithms are called genetic. Easy to adopt for map labeling.

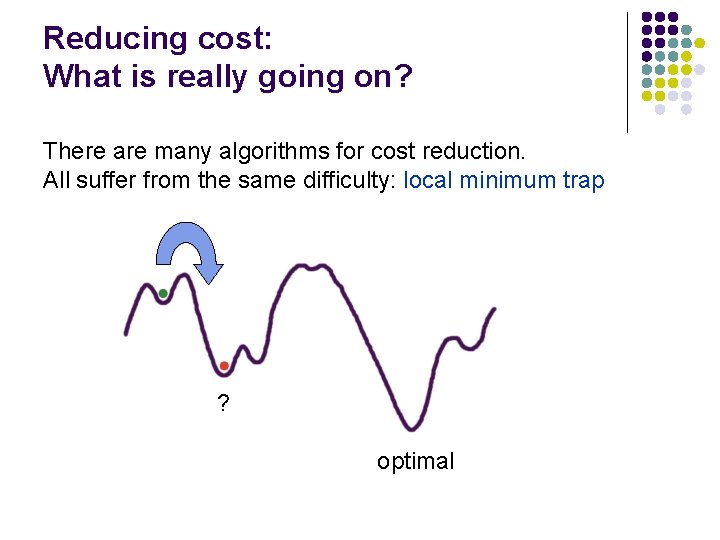
Reducing cost: What is really going on? There are many algorithms for cost reduction. All suffer from the same difficulty: local minimum trap ? optimal

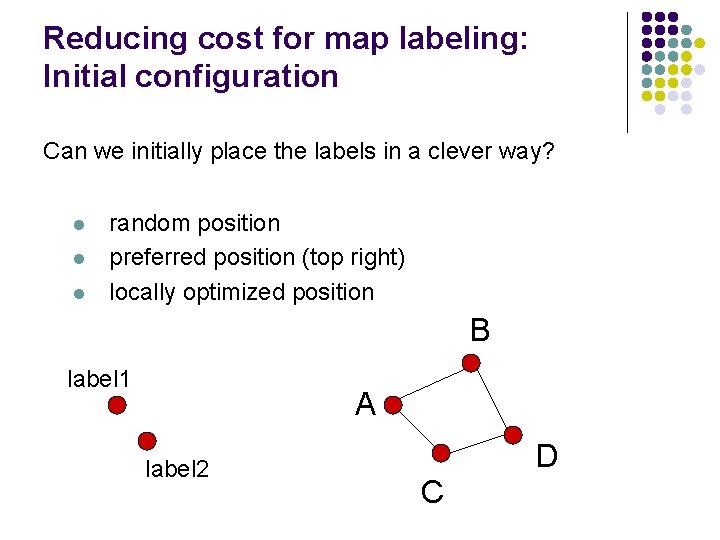
Reducing cost for map labeling: Initial configuration Can we initially place the labels in a clever way? l l l random position preferred position (top right) locally optimized position B label 1 A label 2 D C

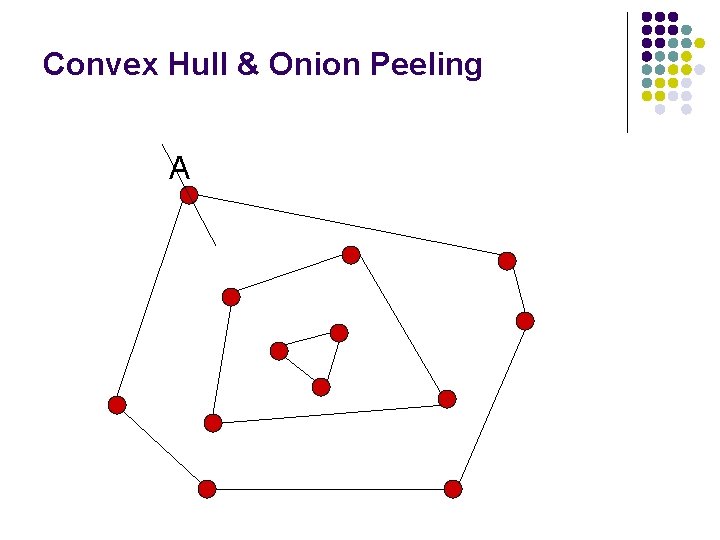
Convex Hull & Onion Peeling A

Onion Peeling is worse than random Onion Peeling was proposed in the literature for map labeling. But it does not work very well (without additional changes). Denver Parker the labels tend to be shifted in similar directions

Implementation Java Applet by Sada and Wan